時速300 km/h 高速列車誘發高架箱梁結構振動特性分析

雷曉燕，王鵬生，翁凌霄，羅 錕

（華東交通大學鐵路環境振動與噪聲教育部工程研究中心，江西 南昌 330013）

隨著高速鐵路的持續快速發展，我國高速鐵路網基本形成。 在已經運營的高速鐵路中，高架線路占比均超過70%。 高架軌道具有占地面積小、能夠避免路基引起的不均勻沉降，有利于高速列車安全平穩運行，缺點是高架橋梁的結構振動與噪聲又造成了新的環境污染。 橋梁結構振動及結構噪聲屬于低頻振動，具有衰減慢，傳播距離遠，影響范圍大，穿透能力強且危害大的特點[1-2]，對環境造成的影響和對人體造成的危害逐漸受到關注[3-4]。 橋梁結構噪聲的機理可歸結為：列車通過時，由于軌道不平順產生的輪軌激勵通過軌枕向下傳遞激起箱梁振動，振動從橋面傳遞到整個箱梁結構，箱梁外表面的振動隨即引起周圍空氣介質的振動并傳播形成噪聲[5]。 由此可見，箱梁振動是高架橋梁結構輻射噪聲的振源，開展高架軌道箱梁結構振動特性及傳遞規律研究，對于高架軌道結構設計及研發減振降噪關鍵技術具有重要意義。

目前，國內外對高架橋上部軌道結構振動特性的研究比較深入[6-8]，而對高架橋梁結構自身振動及其噪聲輻射特性的研究尚待深入。 常用的研究方法包括理論計算、模型試驗和現場測試。 理論方法有積分變換法、有限元法、邊界元法和統計能量法等，這方面已有較多的研究成果[9-11]。 Chu，翟婉明，雷曉燕等針對列車-軌道-橋梁相互作用進行了理論分析和數值模擬[12-14]。 在模型試驗方面，羅錕、曾少輝等[15-16]利用相似律制作相似模型，研究了橋梁彈性支座的隔振效果，并探討了單跨箱梁振動的傳遞特性。在現場實測方面，Nagi 等[17]對香港某箱梁高架橋進行了振動噪聲現場測試，得到了箱梁結構振動和噪聲時域內的規律。 李小珍等[18]基于現場錘擊試驗研究了高鐵簡支箱梁的振動傳遞特性。 理論方法具有建模靈活、 求解手段多樣和可重復性強的優點，但由于在將物理模型簡化為數學模型的過程中存在較多假設，所以計算結果與現場實際情況仍然存在一定的差異。 模型試驗方法具有真實、可靠的優點，但同時也存在成本大、不易操作等缺點。 現場測試受到環境、人員安全、費用等各種條件的制約，有一定的局限性。 因此，在已有研究的基礎上，利用有限元和現場實測相結合的方法研究高速列車作用下高架軌道橋梁結構振動特性及傳遞規律，為高架軌道箱梁結構減振降噪提供理論基礎和技術指導，具有科學意義和工程應用價值。

1 高架箱梁數值仿真模型

1.1 有限元動力學分析理論

利用有限元法進行橋梁結構的振動響應計算，可以得到移動荷載作用下結構隨時間變化的節點位移、速度和加速度。 高架軌道橋梁結構動力學方程為

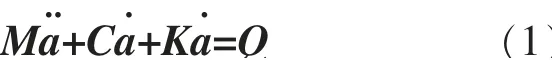
式中：M，C和K 分別為高架軌道橋梁結構的質量矩陣、阻尼矩陣和剛度矩陣；a¨，a˙和a 分別為結構振動的加速度、速度和位移向量；Q為移動荷載向量。高架軌道橋梁結構動力學方程采用Newmark 法求解[19]。

1.2 有限元計算模型與參數

以滬昆客運專線高架軌道箱梁結構為工程背景，橋梁為簡支結構，橋長L=32 m，梁寬D=12 m，梁高H=3.05 m，上部結構為雙線CRTS-Ⅱ型板式無砟軌道，從上到下依次為鋼軌、扣件、軌道板、CA 砂漿層、底座板。在ANSYS 中建立軌道箱梁結構三維有限元模型如圖1（a）所示。 模型包括鋼軌、扣件、軌道板、CA 砂漿層、混凝土底座和箱梁梁體，如圖1（b）所示。

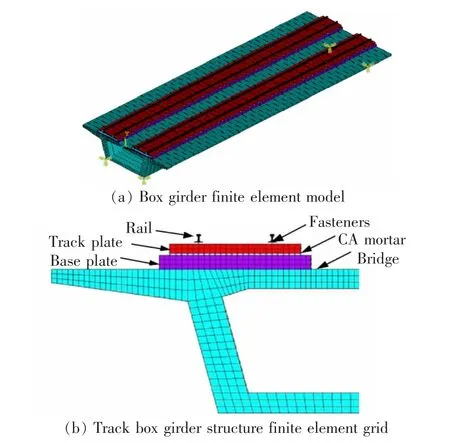
圖1 高架軌道箱梁有限元模型Fig.1 Finite element model of elevated track box girder

箱梁、 混凝土底座和軌道板采用實體單元模擬，鋼軌選用梁單元進行模擬，扣件、CA 砂漿層以及橋梁支座均選用彈簧阻尼單元進行模擬，橋墩簡化為彈性支座，計算參數分別見表1 和表2。

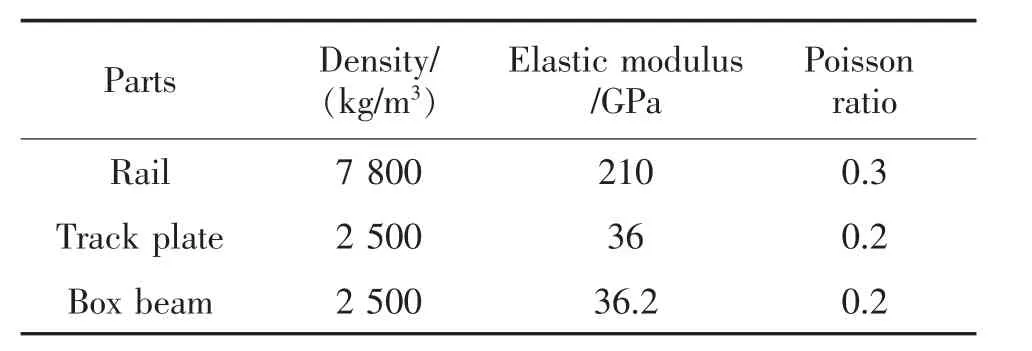
表1 軌道與橋梁結構參數Tab.1 Track and bridge structural parameters

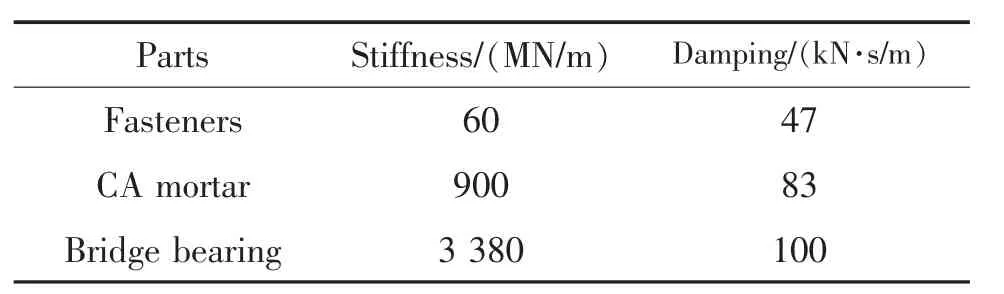
表2 連接部件計算參數Tab.2 Calculation parameters of connecting parts

1.3 輪軌激勵的求解與加載

滬昆客運專線運行的高速列車主要為CRH380A，CRH380B，CRH380C，CRH380D 等，8 節或16 節車輛編組， 列車速度位于300～310 km/h 之間。 基于Matlab 軟件建立車-軌-橋有限元模型， 考慮一節CRH380A 動車，列車速度為300 km/h，并選用德國高速軌道不平順低干擾譜作為軌道隨機不平順激勵源[20-21]，仿真分析列車通過橋梁時誘發高架箱梁結構振動傳遞規律，并提取輪軌作用力，如圖2 所示。

圖2（a）中，vc，φc，vt1，φ1，vt2，φ2分別為車體和前、后轉向架質心豎向位移和繞水平軸轉角；Mc，Jc，Mt，Jt分別為車體和構架的質量和點頭慣量；Ks1，Ks2，Cs1，Cs2分別為車輛一系彈簧和二系彈簧的剛度和阻尼；Mwi，vwi（i=1，2，3，4）分別為車輪質量和豎向位移。

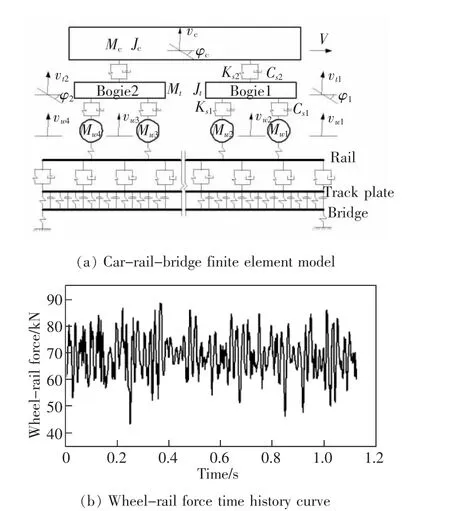
圖2 輪軌力計算模型及輪軌力Fig.2 Wheel-rail force calculation model and time history curve of wheel-rail force

將計算得到的輪軌力看作為隨時間變化的移動荷載，在ANSYS 軟件中利用APDL 語言編寫DO循環，采用節點加載的方式，將輪軌力時程加載到高架橋梁結構上，實現列車過橋的模擬。

2 高架箱梁數值仿真結果

利用上述建立的有限元模型，仿真分析橋梁各個截面以及各板件間的振動響應分布特性。 時速300 km/h，8 節編組的高速動車通過橋梁時間為3 s。沿列車前進方向分別選取支座截面、1/4 截面、跨中截面和3/4 截面作為分析截面，如圖3 所示，其中每個截面的觀測點分別為鋼軌（C1）、軌道板（C2）、底座板（C3）、翼板（C4）、腹板（C5）、底板（C6）和頂板（C7）， 計算得到的各觀測點加速度時域曲線如圖4所示。 對時域數據進行傅里葉變換，得到各觀測點1/3 倍頻程振動加速度級譜，如圖5 所示。

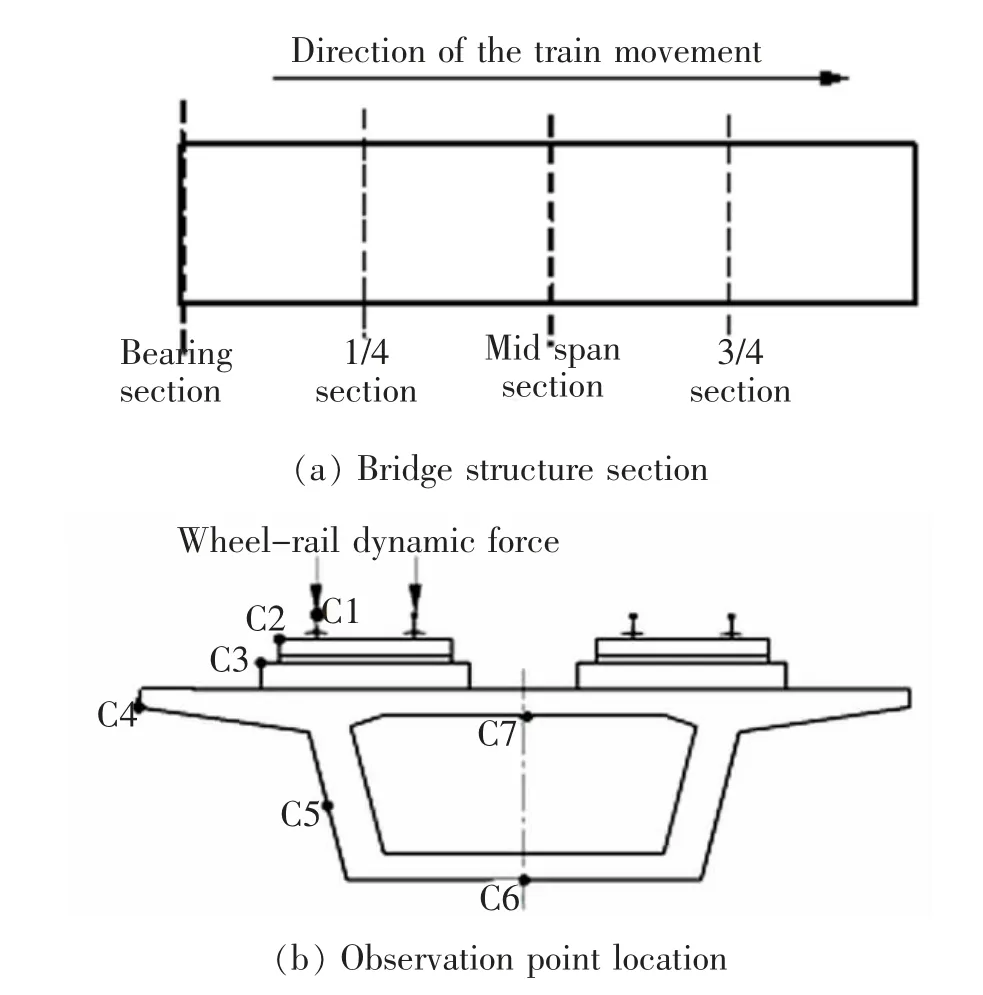
圖3 觀測截面及觀測點位置Fig.3 Observation section and observation point position

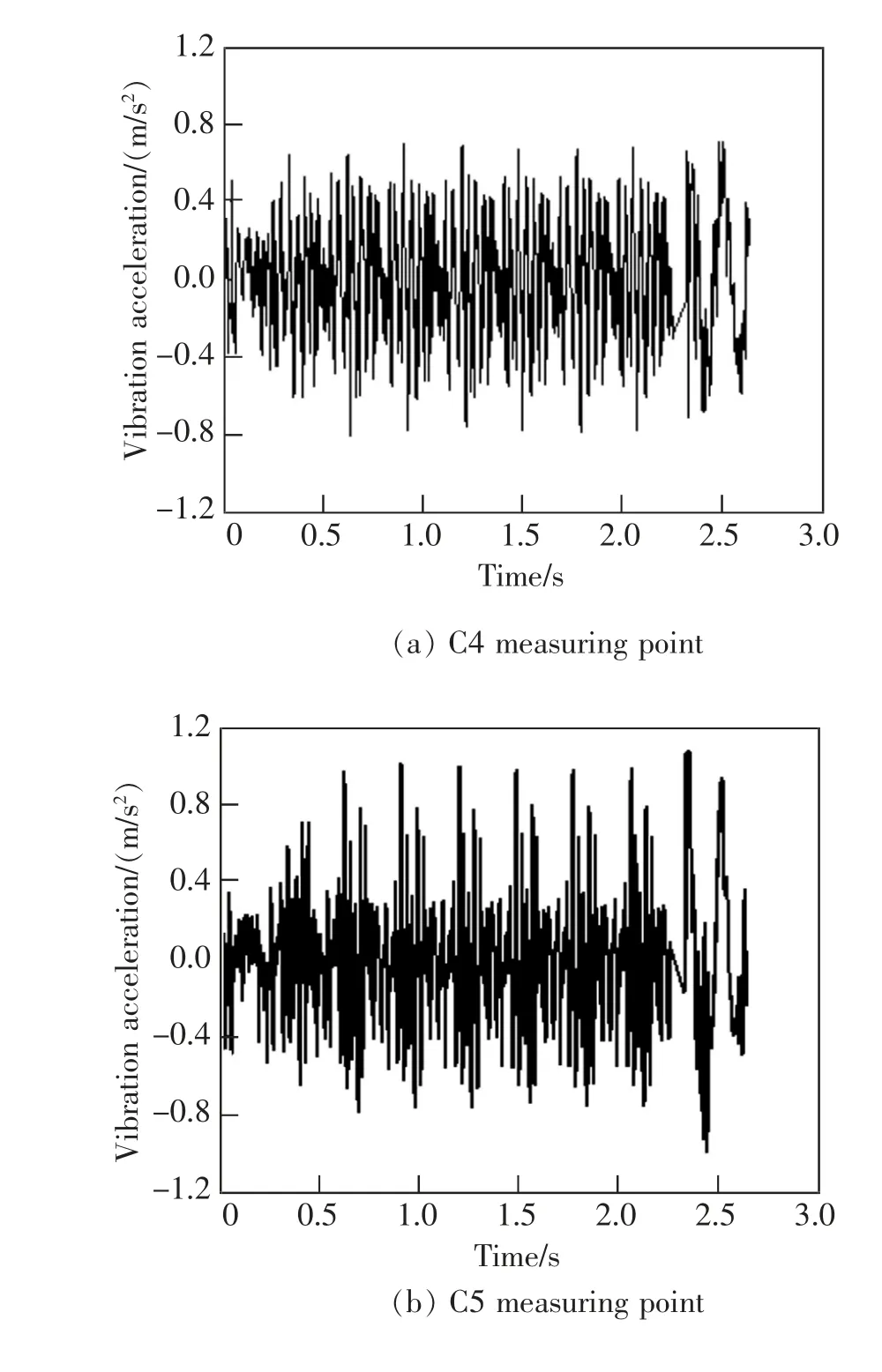
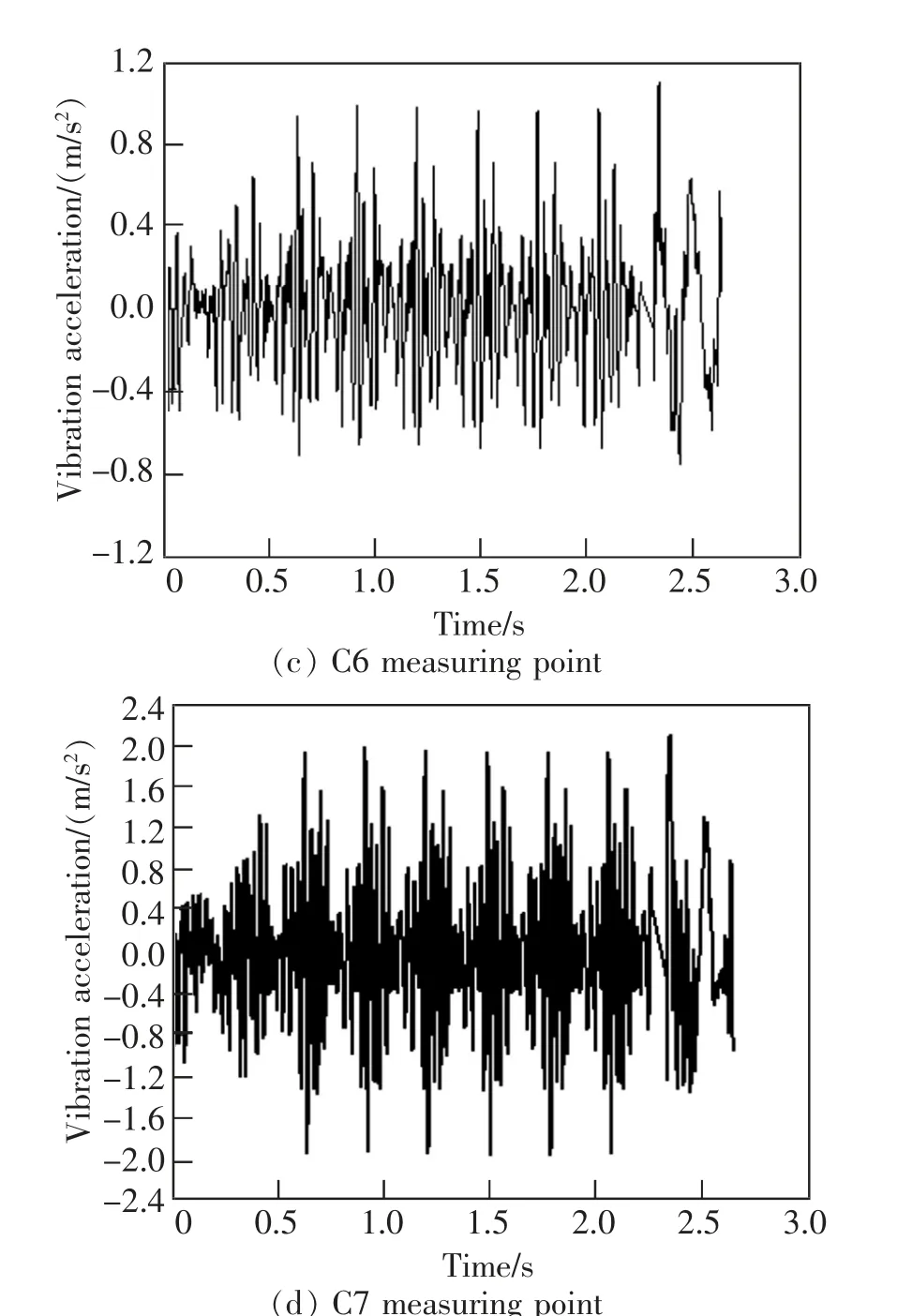
圖4 跨中截面梁體各板件振動加速度時程曲線Fig.4 Time history curve of vibration acceleration of various plates in mid-span beam body

從圖5 可以看出： 梁體振動的優勢頻段在31.5～80 Hz 之間，最大振動加速度級在箱梁頂板位置。 振動在梁體各板件橫向傳遞過程中， 頂板加速度響應最大，底板次之，腹板和翼板相對較小。 表明振動由頂板向翼板的傳遞過程中，加速度響應逐漸減小。而腹板和翼板的響應接近， 體現了箱梁結構振動由接近振源位置向遠離振源傳遞過程中的衰減。

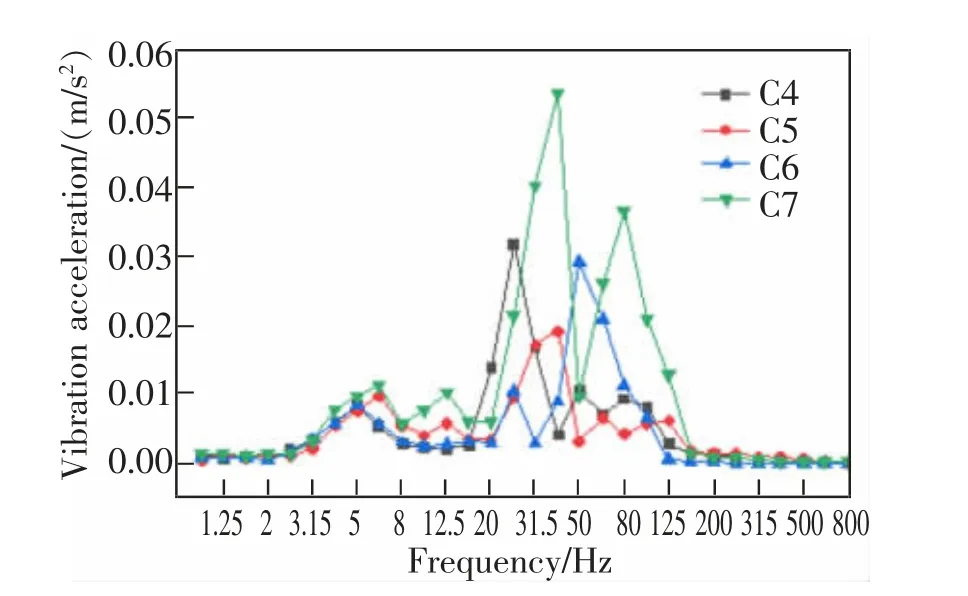
圖5 跨中截面梁體各板件振動加速度頻域曲線Fig.5 Frequency domain curve of vibration acceleration of various plates in mid-span beam body

3 高架箱梁振動特性現場測試

選擇滬昆高鐵高安-南昌區間某高架軌道，對高速列車引起的橋梁結構振動進行現場測試。 測試位置為空曠地帶的橋梁，橋下平坦，橋底面距離地面2.7 m， 軌道結構為雙線CRTS-Ⅱ型板式無砟軌道，橋梁為單箱單室簡支梁，跨度為32 m。為了實測高速列車通過時引起的橋梁結構振動，在橋梁上選取4 個橫截面： 橋梁支座截面，1/4，1/2 和3/4 處截面。 分別在各截面的翼板（Z1 和Z5）、頂板（Z6）、腹板（Z2 和Z4）和底板（Z3）處設置393B04 垂向振動加速度傳感器，如圖6 所示。 采樣頻率為2 000 Hz，列車通過速度為300～310 km/h。

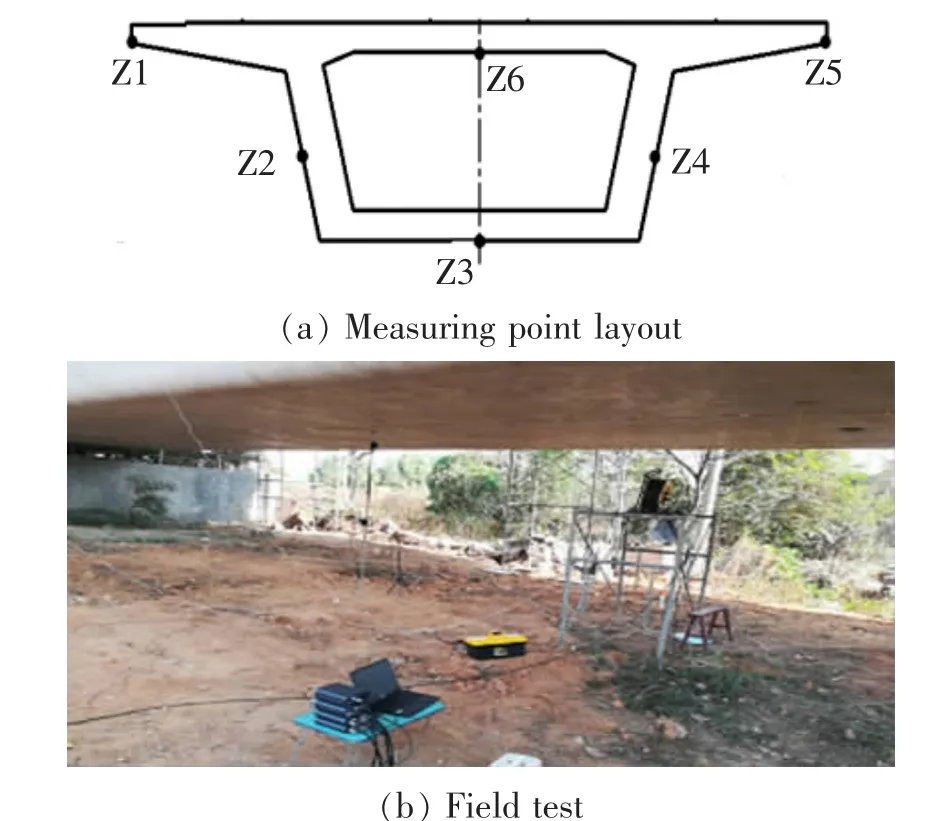
圖6 現場測試振動測點布置Fig.6 Site test vibration measuring point layout

現場試驗共采集到120 組數據， 選取一組典型數據提取各測點的振動加速度時程信號， 如圖7 所示，可以看出頂板、底板、腹板和翼板的振動響應依次減小，即頂板振動＞底板振動＞腹板振動＞兩翼振動。

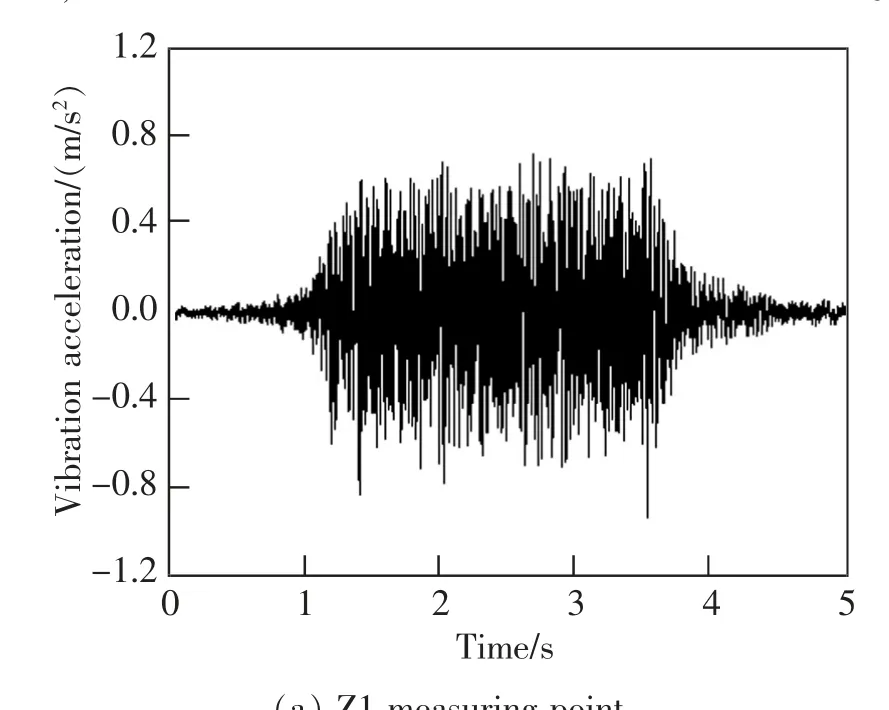
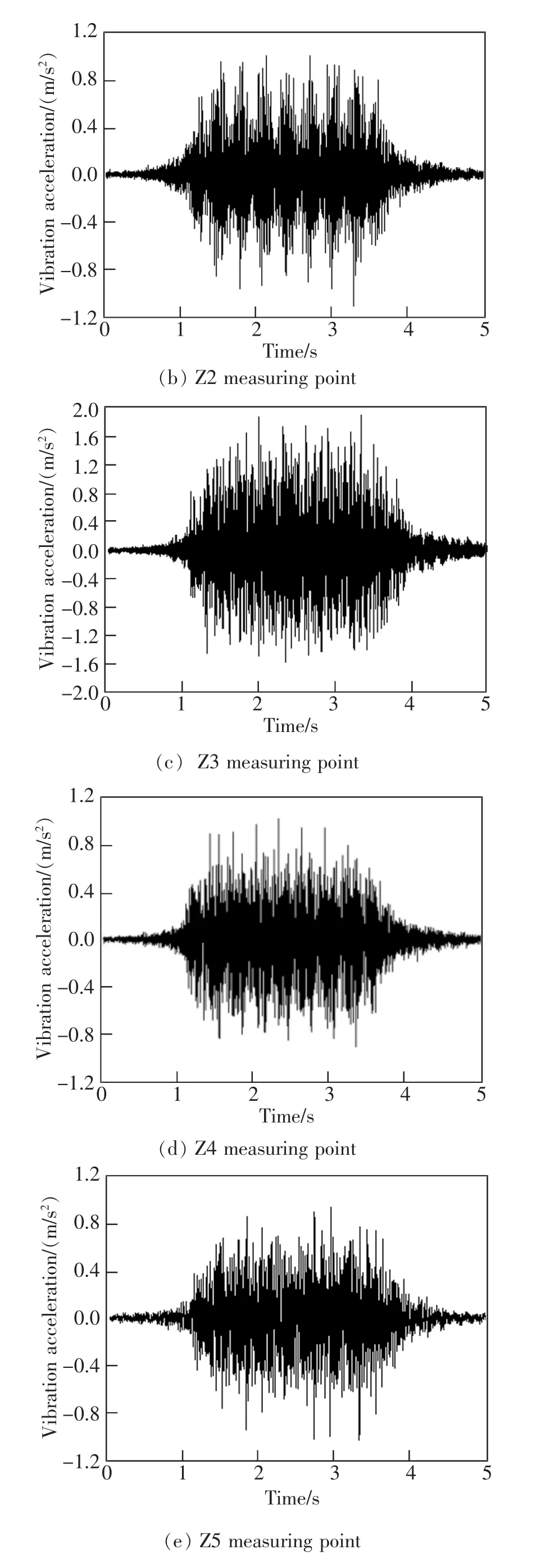
圖7 跨中截面實測振動加速度時程曲線Fig.7 Time history curve of measured vibration acceleration in mid-span section

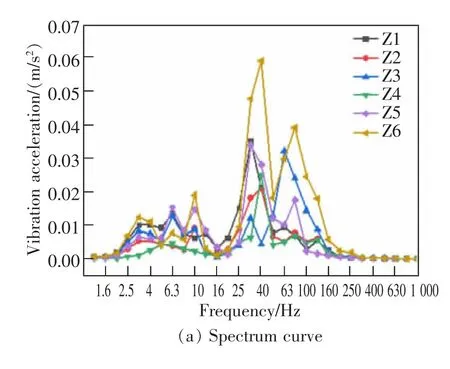
為了分析列車通過時，箱梁結構垂向振動在頻域上的分布特性，對時域數據進行1/3 倍頻程分析，得到相應的振動加速度頻譜曲線。 然后取同向8 節編組列車的20 組數據求平均， 得到跨中截面各測點1/3 倍頻程振動加速度曲線，如圖8 所示。

圖8 表明，在列車荷載作用下，頂板中心振動頻率主要集中在25～100 Hz 范圍內，振動加速度大小為0.020～0.060 m/s2；翼板的振動頻率主要分布在25～80 Hz 范圍內，振動水平為0.010～0.035 m/s2；腹板中心的振動頻率主要分布在30～60 Hz 范圍內，振動水平為0.010～0.025 m/s2；底板中心的振動頻率主要分布在40～100 Hz 范圍內，振動水平為0.005～0.035 m/s2。與時域分析一樣，在25～100 Hz 范圍內，頂板、底板、腹板和翼板的振動響應依次減小。

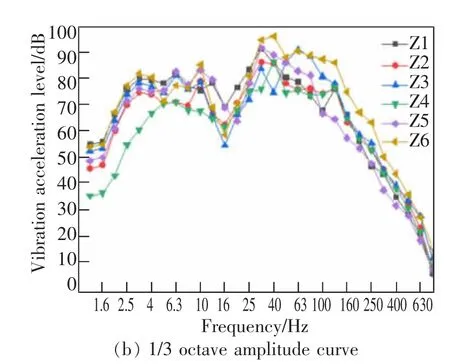
圖8 跨中截面各測點1/3 倍頻程振動加速度曲線Fig.8 1/3 octave vibration acceleration curve of each measuring point in the mid-span section

橋梁結構振動的優勢頻率為31.5～125 Hz，峰值頻率為31.5～63 Hz，在16 Hz 處有一個明顯的波谷；當頻率大于200 Hz 時，橋梁結構加速度振級急劇下降。可以針對31.5～63 Hz 頻率進行橋梁結構減振設計。橋梁頂板最大加速度振級為88.59～100.48 dB，對應的峰值頻率為31.5 Hz 和40 Hz；橋梁底板最大加速度振級為82.96～94.29 dB， 對應的峰值頻率為31.5 Hz 和63 Hz，箱梁底板振動對橋梁結構振動的貢獻最大。

4 數值仿真與實測結果對比分析

4.1 仿真與測試結果對比分析

選取橋梁跨中截面頂板中心、 翼緣板邊緣、腹板中心以及箱梁內梁底測點的實測值與有限元計算值進行對比，仿真計算參數與京滬高鐵橋梁參數一致，對比結果如圖9 所示。

由圖9 可知，在16～200 Hz 范圍內，仿真計算結果與現場實測值吻合良好，實測值平均小于計算值僅為0.001～0.015 m/s2，究其原因，首先是由于忽略了輪面的不圓順對輪軌力的影響， 導致輪軌作用荷載較實際輪軌垂向力要小；此外，由于輪軌橫向力的存在導致箱梁發生橫向扭轉，進而影響垂向振動。但計算模型中的激勵荷載忽略了輪軌橫向力的影響。然而，數值分析結果與試驗結果在10～400 Hz 內變化趨勢基本一致，最大誤差為0.015 m/s2，說明計算模型滿足精度要求。

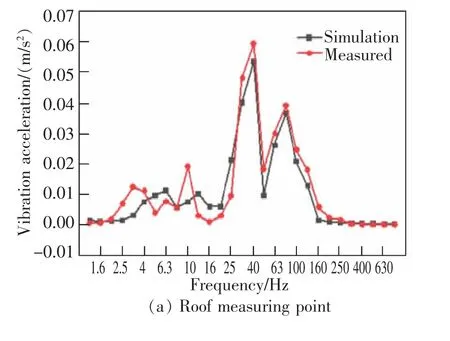
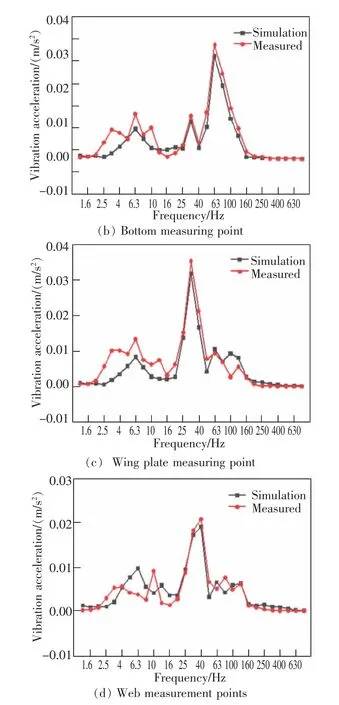
圖9 橋梁各測點振動加速度對比分析Fig.9 Comparative analysis of vibration acceleration at each measuring point of bridge

4.2 不同截面振動響應仿真分析

由于箱梁頂板振動響應最為明顯，以箱梁頂板（C7） 為觀測對象， 考察列車從上橋到下橋的全過程。 從提取到的不同截面位置箱梁頂板（C7）觀測點的位移曲線中，可以發現跨中截面位移最大，1/4 截面次之，梁端截面位移最小，如圖10 所示。 而且3個截面頂板觀測點的位移曲線也近乎一致，位移響應的最大值為0.62 mm。

圖11 為橋梁3 個截面箱梁頂板觀測點的振動加速度頻譜圖。從圖11 可見，時速300 km/h 的高速列車引起橋梁結構振動頻率主要集中在0～200 Hz之間，其中梁端截面的峰值頻率為32.56 Hz，1/4 截面的峰值頻率為37.36 Hz，跨中截面的峰值頻率為19.23 Hz。

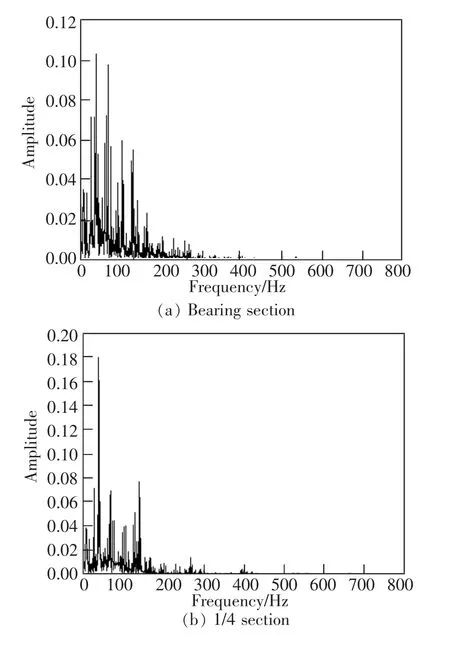
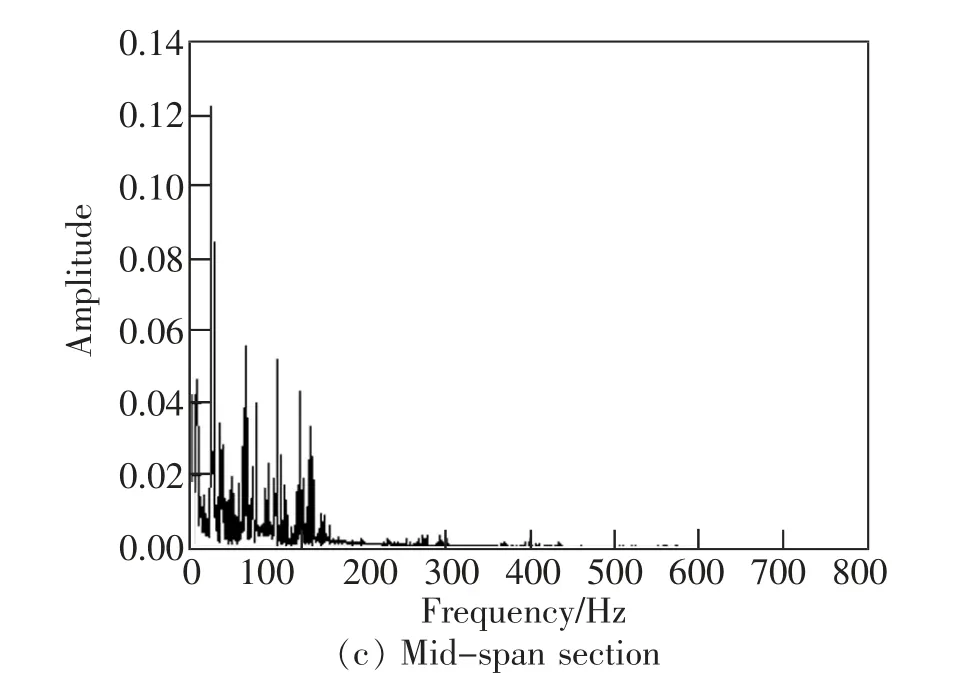
圖11 不同橋梁截面箱梁頂板振動加速度頻譜圖Fig.11 Spectrum of vibration acceleration of box girder roof with different bridge sections

5 結論

通過聯合運用數值方法與現場實測，分析了時速300 km/h 高速列車誘發高架箱梁結構振動特性及傳遞規律，得到以下結論：

1） 橋梁結構振動的優勢頻率為31.5～125 Hz，峰值頻率為31.5～63 Hz，在16 Hz 處有一個明顯的波谷；當頻率大于200 Hz 時，橋梁結構加速度振級急劇下降，可以針對31.5～63 Hz 頻率進行橋梁結構減振設計。

2）橋梁頂板最大加速度振級為88.59～100.48 dB，對應的峰值頻率為31.5 Hz 和40Hz；橋梁底板最大加速度振級為82.96～94.29 dB， 對應的峰值頻率為31.5 Hz 和63 Hz，箱梁底板振動對橋梁結構振動的貢獻最大。

3） 時速300 km/h 高速列車引起箱梁結構振動的規律分別為：頂板垂向振動水平最大，底板次之，翼板和腹板較小，在進行橋梁結構振動控制時應重點關注底板振動，其次是翼板和腹板。

為研究時速300 km/h 高速列車誘發高架箱梁結構振動特性，在數值分析時，首先運用Matlab 軟件建立車-軌-橋耦合系統動力學模型，提取得到的輪軌力時程信息，然后加載到ANSYS 三維軌道-橋梁系統動力有限元模型中，得到軌道和橋梁結構的振動響應。 分析結果與實測數據吻合良好證明了該方法的有效性。