2018年10月-2019年9月太原大氣能見度與相對濕度及PM2.5濃度的關系研究

盧盛棟，趙桂香，金 磊，李 強

(1.山西省氣象災害防御技術中心，太原 030012；2.山西省氣象臺，太原 030006)

大氣能見度與人們生活密切相關，低能見度往往誘發交通事故，造成飛機延誤等。近年來，大氣能見度的變化已引起各界重視。相關研究表明[1-10]，大氣能見度不僅與當地污染物有關，還與相對濕度及顆粒物濃度密切相關。呂建華等[10]研究表明，濟南市大氣能見度與相對濕度、細顆粒物濃度有明顯的月變化和日變化規律。濟南市大氣能見度與相對濕度的相關系數為0.6501，與PM2.5濃度的相關系數為0.7422。吳雁等[11]對河北中南部城市大氣能見度與細顆粒物濃度進行了分析，發現PM10和PM2.5濃度與能見度呈顯著的負相關關系，且與PM2.5濃度相關性更加顯著。此外，當大氣中污染物濃度較高時，較小風速不能促使污染物擴散，也會出現低能見度現象[12-15]。

關于大氣能見度與顆粒物濃度及相對濕度的關系模型研究，廣大學者也進行了探討[16-20]。胡海川等[17]研究了神經網絡在環渤海地區能見度預報中的應用，發現該方法對低能見度天氣過程的能見度預報效果良好，能見度低于10 km的預報誤差為4～6 km。白永清等[18]揭示了武漢大氣能見度與PM2.5濃度存在的非線性相關關系，用神經網絡方法得到了武漢地區大氣能見度預報模型。宋明等[19]利用相對濕度、PM2.5及PM10濃度數據，用指數函數擬合了能見度與PM2.5及PM10濃度的關系，用非線性擬合的方法得到了天津地區大氣能見度預報公式。王曉敏等[20]利用指數函數擬合了能見度與相對濕度的關系，并用非線性擬合方法得到了石家莊地區能見度預報公式。這些模型對本地區能見度預報都有一定的適用性。

太原作為山西省省會，重工業比較集中，三面環山，大氣常處于一種靜穩狀態，不利于顆粒物的擴散，常造成低能見度天氣[21]。相比于長江三角洲、京津冀等發達地區，關于太原地區大氣能見度的研究較少。盧盛棟等[21]分析了太原大氣能見度月平均最大值出現在5月，月平均最小值出現在1月。管琴等[22]利用2009年太原地區日平均能見度、相對濕度、空氣污染指數進行擬合，建立了太原地區霧天能見度預報模型，該模型有一定適用性。由于近幾年太原城市擴容加速，與南邊的晉中市榆次區、太谷區同城化發展，都市圈中心逐漸南移，特別是近幾年山西轉型發展步伐加快，污染物傳輸也發生了改變，相對濕度、顆粒物濃度對能見度的影響發生了變化，因此本文利用2018年10月-2019年9月太原地區能見度、相對濕度及PM2.5質量濃度逐小時觀測數據，研究分析了大氣能見度與相對濕度及PM2.5濃度的關系，采用多元非線性擬合[23-24]及神經網絡[25-29]方法構建了能見度預報模型，并利用太原地區近期氣象數據對兩種預報模型進行了檢驗及對比分析，以期為太原地區能見度預報提供參考。

1 資料與方法

利用2018年10月-2019年9月太原小店區氣象觀測站(112.55°E、37.75°N，海拔776.2 m)大氣能見度(傳感器型號：HY-V35)、相對濕度(傳感器型號：HMP155)、PM2.5濃度(傳感器型號：TEOM-1405D)逐小時觀測數據，經質量控制去掉奇異值，分析能見度與相對濕度及PM2.5濃度的定量關系，并利用非線性擬合及神經網絡方法構建了能見度預報模型。

非線性擬合是采用迭代法對模型進行擬合，應用非線性最小二乘法確定參數取值范圍，根據可決系數比較擬合效果，選取誤差最小的模型，確定自變量與因變量之間的非線性關系。本文非線性擬合借助SPSS軟件完成。

神經網絡具有良好的處理非線性問題的能力，有信號前向傳遞、誤差反向傳播的特點[30]。采用輸入層、隱含層、輸出層三層結構，在前向傳遞中，輸入信號從輸入層、隱含層逐層處理至輸出層，如果輸出層得不到期望值，則轉入反向傳播，根據誤差不斷調整權值和閾值，使輸出不斷逼近期望值[21]。本文隱含層節點數設定為10，一般情況下提高隱含層節點數可以提高神經網絡收斂精度，但隱含層過多，會出現過擬合現象，對樣本識別能力下降。本文神經網絡模型是通過MATLAB軟件編程實現的。

在對預報模型進行檢驗時，用到均方根誤差(ERMS)、平均絕對百分誤差(EMAP)。計算方法如下：

(1)

(2)

式(1)—(2)中，P代表預報值，O代表觀測值，N代表檢驗樣本個數。

2 結果與分析

2.1 太原大氣能見度與相對濕度的關系

利用太原地區2018年10月-2019年9月相對濕度及能見度逐小時數據(除去降水及奇異值，樣本量為6153)，統計分析不同相對濕度對應的平均能見度及平均PM2.5濃度數據，散點圖見圖1。由圖1可知，當相對濕度RH<40%時，隨著RH升高能見度下降相對較快，對應PM2.5濃度也上升較快；當相對濕度40%≤RH<90%時，隨著RH升高，PM2.5濃度基本不變(圖1b)，能見度下降緩慢(圖1a)，出現圖1(a)第一個拐點(橫坐標40%對應的點，屬于兩種擬合曲線交叉點)；高濕條件下，即RH≥90%時，隨著RH升高，能見度急劇下降，出現圖1(a)第二個拐點(橫坐標90%對應的點，屬于兩種擬合曲線交叉點)。這也與曹軍驥等[31]的研究比較一致，即隨著相對濕度的升高，可溶性氣溶膠吸濕潮解造成散射效率顯著增強，能見度惡化，當相對濕度RH≥90%時，這種現象更為顯著。

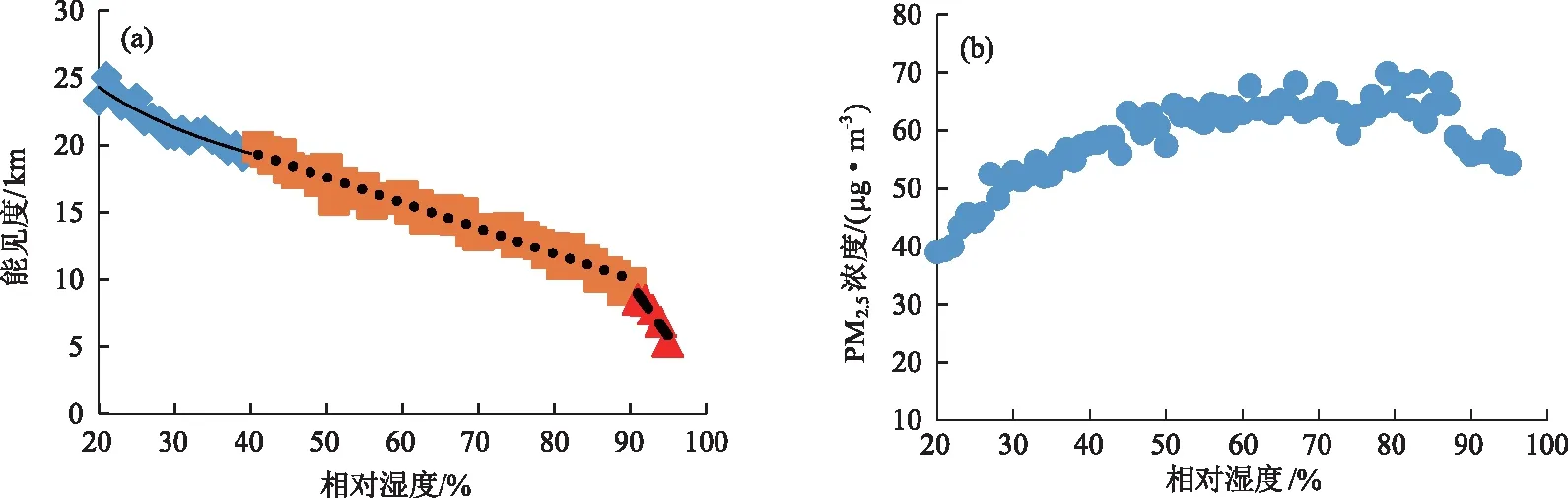
圖1 太原大氣平均能見度、PM2.5濃度與相對濕度的關系

由圖1(a)的散點圖，得出太原地區大氣能見度(V)與相對濕度(RH)的定量關系式如下：

(3)

當RH<40%時，太原大氣能見度與相對濕度成冪函數關系，如式(3)所示，二者相關系數達到0.93；當40%≤RH<90%時，太原大氣能見度與相對濕度呈線性關系，相關系數達到0.96，且在此條件下，相對濕度每增加1%，太原平均能見度降低0.188 km；當RH≥90%時，太原大氣能見度與相對濕度呈二次多項式關系，相關系數為0.97，且在此高濕條件下，隨著相對濕度增加，能見度急劇下降。

2.2 太原大氣能見度與PM2.5濃度的關系

依據2018年10月-2019年9月太原小店區逐時氣象數據及顆粒物濃度數據，分析PM2.5濃度對能見度的影響。為盡可能消除相對濕度對能見度的影響，本文將相對濕度分成五個區段進行分析[18]，并采用冪函數擬合PM2.5濃度與能見度的散點關系，如圖2所示。

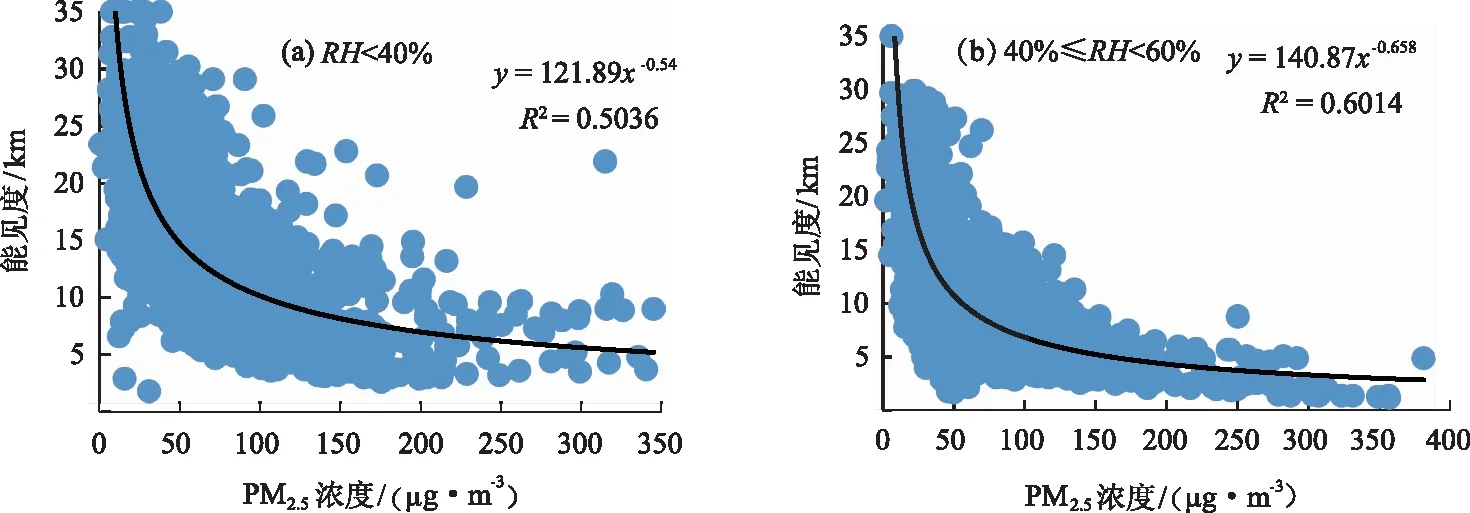
圖2 不同濕度區段下太原地區大氣能見度與PM2.5濃度的擬合關系

白永清等[18]得出PM2.5濃度與武漢地區大氣能見度的相關系數為0.73～0.84，而太原地區各濕度段二者相關系數指標為0.32～0.67(見表1)，特別當RH≥90%時，二者相關系數僅為0.32，模型擬合較差，但都通過了0.01的顯著性水平檢驗。此外，相對濕度在80%≤RH<90%區段下，武漢能見度與顆粒物相關性最強[18]，廣州在40%≤RH<60%區段下的相關性最強[32]，而太原在40%≤RH<60%區段下，決定系數為0.60，相關系數為0.67，該時段相關性最強，表現出的地域性差異，可能與太原三面環山北高南低特有的地形有關。

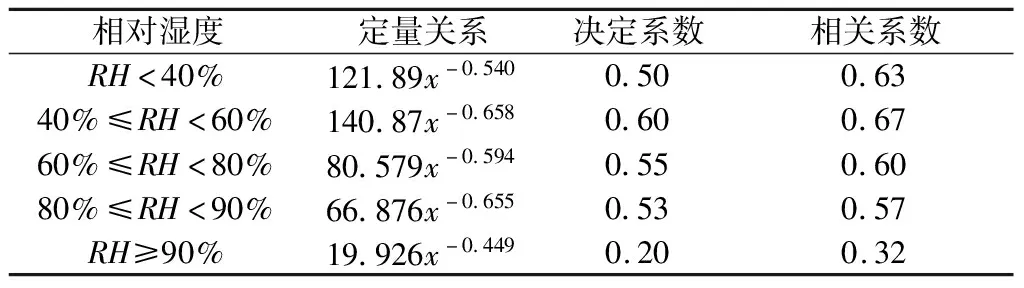
表1 不同濕度區段下太原地區大氣能見度與PM2.5濃度的擬合方程

2.3 能見度預報模型

2.3.1 非線性擬合構建預報模型

由以上分析可知，相對濕度與PM2.5濃度對大氣能見度影響顯著，現以其為因變量，將相對濕度分成五個區段，利用SPSS軟件對大氣能見度進行多元非線性擬合，結果如下：

V=a×RHb+c×ρ(PM2.5)d+e

(4)

式(4)中，V代表大氣能見度，RH代表相對濕度，ρ(PM2.5)代表PM2.5濃度，a-e為系數。從擬合結果看(見表2)，均方根誤差、平均絕對百分誤差分別在4.59～6.71 km、25.99%～63.56%。當RH<90%時，相關系數在0.70左右，當RH≥90%時，模型較差些，相關系數僅為0.40，但都通過了0.01的顯著性檢驗，說明該模型對大氣能見度具有一定的預報能力。

表2 不同濕度區段下大氣能見度與相對濕度及PM2.5濃度的非線性擬合系數

2.3.2 神經網絡構建能見度預報模型

將相對濕度和PM2.5濃度預報因子作為輸入端，能見度預報值作為輸出端，采用太原地區2018年10月-2019年9月逐時數據，分為兩段，前3/4長度為訓練期，后1/4作為預報期，構建神經網絡大氣能見度預報模型。

神經網絡模型在預報期內模擬與實況值的變化趨勢基本一致，特別是對低能見度樣本，模擬效果更佳(見圖3)。對神經網絡構建的大氣能見度預報模型進行檢驗，相關系數為0.82，均方根誤差為3.42 km，平均絕對百分誤差為26.15%。對比非線性擬合結果，相關系數為0.40～0.76，均方根誤差為4.59～6.71 km，平均絕對百分誤差為25.99%～63.56%，神經網絡預報模型更具有較高準確性。

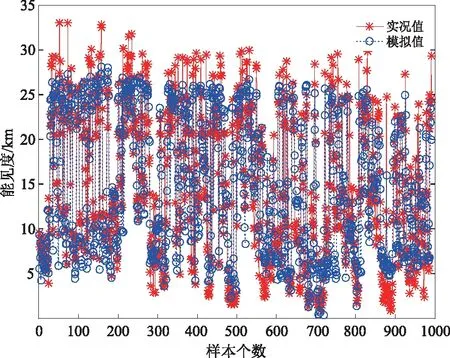
圖3 神經網絡模型預報期內能見度預報與實況對比

2.4 預報模型驗證

2020年1月，太原地區低能見度現象頻發，全月低能見度天氣現象占全月總比達70%，特別是在1月8-12日，太原地區出現連續5 d的低能見度，城區實行了交通管制。為此，利用太原市小店區2020年1月1-31日氣象小時數據對模型進行驗證。

圖4為兩種模型的預報效果。由圖4可以看出，兩種預報模型對能見度都有一定的預報能力。非線性模型的預報值偏高且較為分散，神經網絡預報值更向對角線集中。由兩個模型的預報結果(表3)可知，神經網絡預報模型預報值與實況值的相關系數提高到了0.91，均方根誤差僅為2.77 km，平均絕對百分誤差降到了24.88%。

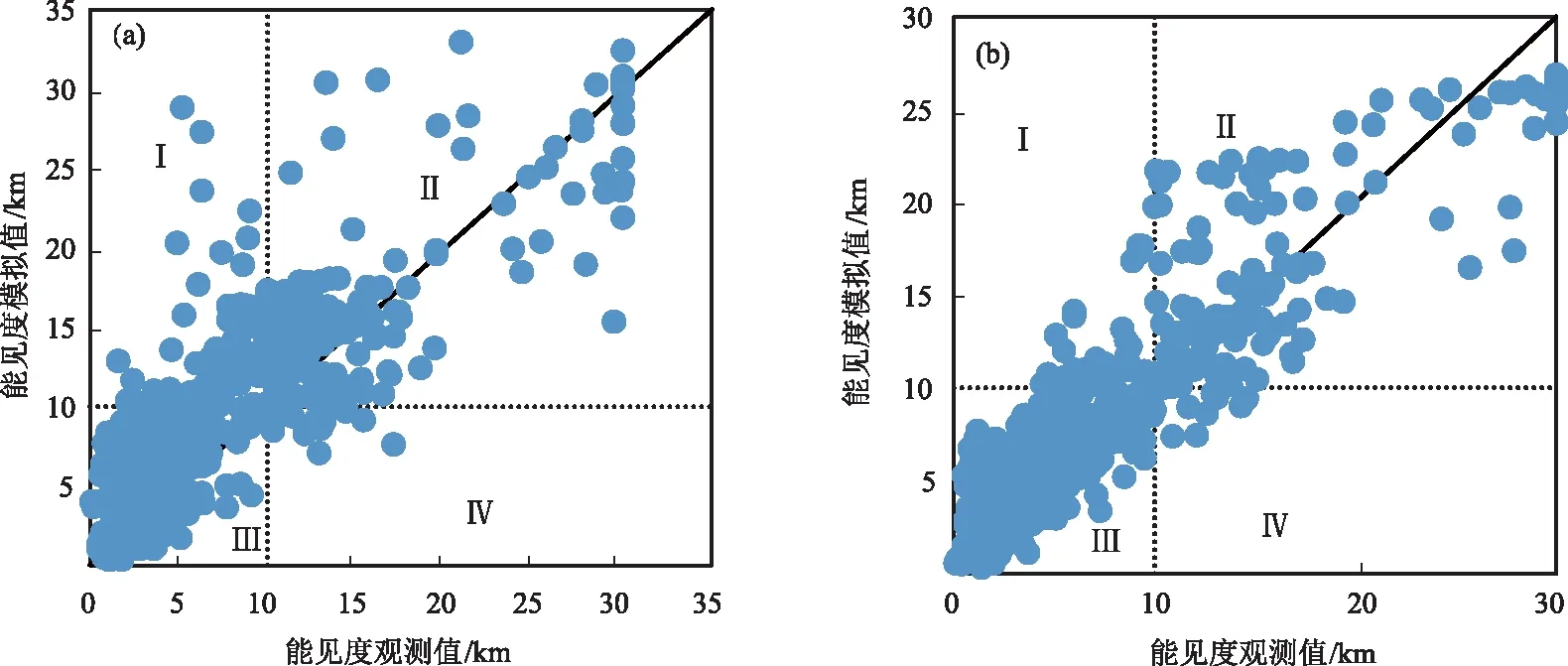
圖4 非線性預報模型(a)和預報模型(b)的預報效果

表3 兩種不同預報模型的檢驗參數

以低能見度閾值10 km為分界線[33]進行分級檢驗，將圖4中分成四個區域(圖中虛線部分)Ⅰ、Ⅱ、Ⅲ、Ⅳ，落在各自區域的點數分別為a、b、c、d，根據散落在各自區間的點數代入對應公式分別計算預報準確率、漏報率、空報率[28,34]，以此來評價其預報能力，統計結果見表4。由表4可知，兩種預報模型對大氣能見度都有一定的預報能力。非線性擬合的預報準確率高達84.53%，神經網絡的準確率提高到了93.78%；非線性擬合模型的漏報率較高，神經網絡模型的漏報率降至6.34%；兩種預報模型的空報率都較低，神經網絡模型的降至1.85%。兩種預報模型的誤差頻率分布都較好地服從正態分布(見圖5)，但神經網絡模型的誤差集中在2 km以內，落在該區域的頻率達74.72%，非線性擬合的誤差較為分散，主要集中在4 km以內，落在該區域的頻率為90.74%，在2 km以內的頻率僅為63.26%。

表4 兩種不同預報模型的分級檢驗

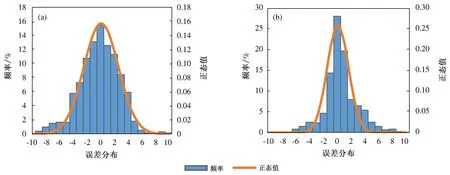
圖5 非線性預報模型(a)和神經網絡預報模型(b)誤差的頻率分布

綜上分析，兩種模型對大氣能見度都有一定的預報能力，但神經網絡模型預報能力更強。由于神經網絡模型比較抽象，非線性擬合模型參數比較固定，在實際應用中可以將兩者結合起來使用。

3 結論與討論

利用2018年10月-2019年9月太原小店區相對濕度、PM2.5濃度、能見度逐小時觀測數據，分析了能見度與相對濕度、PM2.5濃度的關系，利用非線性擬合及神經網絡方法，構建了關系模型，并進行了檢驗，得到以下結論：

(1)細顆粒物濃度與相對濕度對太原大氣能見度有明顯影響。當RH<40%時，能見度降低主要是由PM2.5濃度逐漸升高影響，能見度與相對濕度呈非線性關系；當40%≤RH<90%時，能見度與濕度呈線性關系，濕度每增加1%，太原大氣能見度平均降低0.188 km；當RH≥90%時，隨著相對濕度增加，能見度急劇下降。不同濕度條件下，太原大氣能見度與PM2.5濃度呈冪函數關系，相對濕度在40%≤RH<60%區段下相關性最強。

(2)不同相對濕度條件下非線性擬合的大氣能見度預報模型的相關系數為0.40～0.76，均通過了0.01的顯著性水平檢驗，均方根誤差為4.59～6.71 km，平均絕對百分誤差為25.99%～63.56%，擬合模型在RH<90%時，擬合效果最佳。神經網絡構建的大氣能見度預報模型預報性能良好，相關系數為0.82，均方根為3.42 km，平均絕對百分誤差為26.15%。

(3)利用太原小店區2020年1月小時數據對非線性擬合模型和神經網絡模型進行了驗證，結果表明，兩種模型對太原地區大氣能見度都有一定的預報能力，但神經網絡模型預報準確率達93.78%，漏報率和空報率都比非線性擬合模型的低，且誤差分布比較集中，集中在2 km以內的達74.72%，非線性擬合模型的誤差分布較分散，多集中在4 km以內，在2 km以內的誤差達63.26%。神經網絡模型較非線性模型預報結果更準確，但非線性模型更形象，實際業務中可以將兩者結合使用。

影響能見度的氣象因子較多，如風速、風向及高空氣象要素等對能見度也有影響，且文中資料數據僅為2018年10月-2019年9月的，觀測站點為小店觀測站，在后期研究中將進一步增加能見度氣象影響因子，延長時間序列及站點序列，以得到更準確的能見度模型。