基于彈性變分模態提取的時間相關單光子計數信號去噪*

汪書潮 蘇秀琴 朱文華 陳松懋張振揚 徐偉豪 王定杰

1) (中國科學院西安光學精密機械研究所, 中國科學院空間精密測量技術重點實驗室, 西安 710119)

2) (中國科學院大學, 北京 100049)

3) (青島海洋科學與技術試點國家實驗室, 青島 266237)

單光子激光雷達的回波信號具有極低的信噪比, 有效地消除噪聲和提取出回波信號特征是提升單光子激光雷達測距精度的關鍵, 變分模態分解算法需要使用者依據經驗確定分解本征模態函數數量, 不具有適用性和通用性.為此, 本文基于時間相關單光子計數信號特點, 提出了在變分模態分解中讓信號按照指定頻率進行聚類分解的變分約束條件, 并采用彈性網回歸重構不適定問題的求解模型, 提出了彈性變分模態提取算法.實驗結果表明, 在波段850 nm、平均發射功率為25 nW、背景噪聲平均功率為19.51 μW的條件下, 利用該方法, 得到了時間相關單光子計數信號重建精度的均方根誤差為1.414 ns.同時在不同的累積時間下, 能夠穩定且快速地提取出回波信號特征, 有效地提高了算法的去噪能力和特征提取的性能.

1 引 言

時間相關單光子計數技術目前是激光雷達領域中前沿的研究方向之一.該技術采用時間相關單光子計數器(time-correlated single photon counter,TCSPC), 對單光子探測器的輸出信號進行統計分析, 將激光雷達的探測能力提升到了單光子級, 進一步提升了激光雷達的探測范圍和測距精度.本技術在天地目標識別[1]、水下目標探測[2]、非視域成像[3]、遠距離激光三維成像[4]、生物學醫療[5]和大氣觀測[6]等眾多領域都有廣泛的應用前景.

近年來, 基于時間相關單光子計數技術的應用在各個領域逐步普及.Aurora等[2]實現了無背光環境下, 水下6.7個衰減長度的動態目標成像;David等[3]實現了對隱藏目標進行激光器到墻面的距離為1 m、分辨率為512 × 512的非視域成像, 累積時間長達50 min; Li等[4]實現了夜間對45 km外目標進行三維成像.這些應用都是在弱噪聲環境、長累積時間等理想條件下進行的.這是由于時間相關單光子計數技術易受噪聲干擾, 尤其是在白天強太陽背景光的情況下, TCSPC會受噪聲光子堆積效應的影響, 有效信號完全被噪聲淹沒.同時, 由于該技術采用的單光子探測器, 對回波信號的響應和器件本身的熱噪聲響應均服從泊松分布[7], 是典型的非平穩信號(時間序列), 由于非平穩信號穩定性差、隨機性強、易與其他信息混疊[8],從中提取出有效信號十分困難.此外單光子探測器需要對回波信號進行累積, 累積時間與信號信噪比呈正相關, 而總累積時間直接影響探測過程的實時性, 很難平衡探測時間和信噪比之間的關系.

為了從被噪聲污染的非平穩信號中提取有效信息, 可以采用圖像后處理的方法, 文獻[9]和文獻[10]利用相鄰像素之間的關系進行去噪, 但處理實時性差; 也可以采用信號分解的方法, 相關學者已經取得了諸多研究成果, 獲得較為廣泛應用的方法有小波變換(wavelet transform, WT)[11]、希爾伯特振動分解(Hilbert vibration decomposition,HVD)[12]、經驗模態分解(empirical mode decomposition, EMD)[13]和自適應噪聲總體集合經驗模 態 分 解(complete ensemble empirical mode decomposition method based on adaptive noise,CEEMDAN)[14]等.WT算法構建了可隨頻率改變的窗口函數, 可以方便地分離出目標信息, 但需要人為地針對信號特征選取小波基, 且分解結果包含無意義的諧波成分[15].HVD算法則采用的是希爾伯特變換和低通濾波的組合, 會產生端點效應[16].EMD算法在分解過程中用包絡線進行擬合, 會引起端點效應和模態混疊[17]; CEEMDAN算法作為EMD的改進, 減小了模態混疊, 但依然無法避免端點效應, 且計算復雜度大幅度增加[18].

鑒于上述方法存在的諸多問題, Dragomiretskiy等[19]提出了變分模態分解(variational mode decomposition, VMD)算法, 它是一種包含Wiener濾波和Hilbert變換的新型模態分解算法, 并將求解本征模態函數(intrinsic mode function, IMF)這一變分問題通過Parseval/Plancherel等距變換映射到頻域.因其具有完備的數學理論基礎, 對非平穩信號進行VMD分解時, 克服了EMD類經驗分解算法存在的端點效應和模態混疊問題, 從而對非平穩信號有著更強的適應性.然而, VMD無法提取特定頻率范圍內的信號, 當其分解模態數量參數M確定了之后, VMD算法會按頻率從低到高對信號進行分解, 而感興趣的信號往往和其他頻率的噪聲信號混疊在一起, 要想將目標頻段的信號分離出來, 只能手動調節分解模態數量, 不僅提升了計算復雜度, 也降低了算法的適用性[20].針對這些問題, 國內外學者開展了更加深入的研究.文獻[21]在VMD算法基礎上增加了新的迭代停止判定條件,具有較高的收斂速度; 文獻[22]提出采用神經網絡優化VMD算法參數; 在文獻[23]和文獻[24]中則結合不同類型的群優化算法, 基于信號的特征, 確定最優的模態分解的層數.這些改進方法僅考慮模態函數數量對分解效果的影響, 而忽略了底層不適定問題模型對迭代的影響, 從而導致分解效果不佳.

為了進一步提高非平穩信號的重建精度, 同時提升重建方法的通用性和適應性, 本文提出了一種新的非平穩信號的時頻分解方法, 稱為彈性變分模態提取(elastic variational mode extraction, EVME).此方法對以時間相關單光子計數信號為例的非平穩信號進行分析, 增加了信號按照在指定頻率進行聚類分解的變分約束條件, 并采用彈性網回歸重構了變分模態分解中基于吉洪諾夫(Tikhonov)正則化的不適定問題的求解模型, 從而改進算法結構,提升其性能.利用本文所提出的方法對噪聲條件下的時間相關單光子計數信號進行處理, 并與相關非平穩信號處理算法進行對比, 以驗證本方法的性能.

2 彈性變分模態提取方法

2.1 理論基礎

VMD算法通過迭代來搜索將實信號 f (t) 分解為若干個本征模態函數的組合, 其本質是將時域上的不適定問題用Tikhonov正則化轉換為適定問題, 再映射到頻域上, 構建成變分約束問題進行求解.求解出來的本征模態函數組在頻域上從低頻到高頻分離, 每一個本征模態函數都需要估計其中心頻率和帶寬, 且所有本征模態函數的估計帶寬之和最小.VMD算法對應的約束變分模型為:

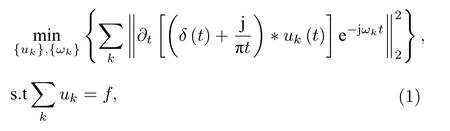
其中, { uk(t)}={u1(t),u2(t),···,uM(t)} 是分解后的M個本征模態函數,{ωk}={ω1,ω2,···,ωM}為對應的中心頻率, *為卷積運算, ∥·∥ 為 范數,δ(t)為單位沖激函數.

通過交替方向乘子法(alternating direction method of multipliers, ADMM)[19]將上述變分約束求極值問題轉變成凸優化問題, 寫出對應約束變分模型的增廣Lagrange方程:

其中, λ為Lagrange乘子, α 為懲罰因子, 〈 ,〉 代表兩個向量的點積.再利用對偶上升法求解出uk,ωk和 λ 在頻域內的迭代算式.

利用VMD算法將信號分解成M個本征模態函數的步驟如下.

2) u ?k(ω) 和 ωk分別由(3)式和(4)式迭代得出:

3) λ通過(5)式迭代更新確定,

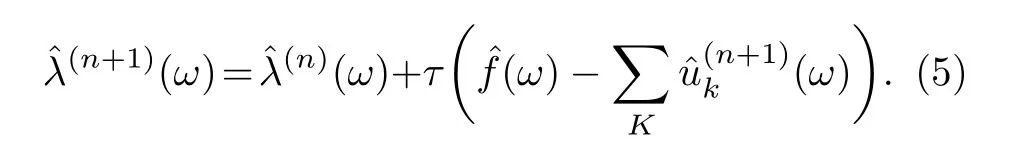
4) 重復運行步驟2)和步驟3)直到滿足迭代的停止條件

(3)式—(6)式中, 上標 ∧ 代表傅里葉變換, 右上角標(n)和(n+1)為迭代次數, 右下角標k表明對應第k個分解模態, τ 為更新參數, ε 為判別精度, 且有 ε >0.

5) 輸出M個本征模態函數 { uk}.

2.2 彈性變分模態提取原理

本文提出的彈性模態提取算法是時頻信號分解方法, 它相較于原始的變分模態分解算法, 增加了變分約束條件, 讓信號按照在指定頻率進行聚類分解, 通過得到模態中心頻率的近似值, 可以提取出一個中心頻率在預定模態附近的本征模態, 讓信號按照預設中心頻率進行聚類提取, 而無需人為地調節分解模態的個數.同時, 本文方法采用彈性網回歸重新構建不適定問題的求解模型, 從2-范數和1-范數結合的角度來對代價函數進行有偏分析,克服了基于Tikhonov正則化的VMD算法帶來的回歸結果失真問題, 讓信號分解更加精確.

彈性模態提取算法的推導過程如下.

首先構建本文提出的彈性模態提取算法的變分約束模型, 設輸入信號 f (t) 被分解為兩種信號:期望模式 ud(t) 和殘差信號 fr(t) , 如下所示:

本文提出的方法建立在以下基礎上.

1) 所期望的模態應該緊湊地圍繞其中心頻率.VMD算法通過Tikhonov正則化將病態問題轉化為適定問題, 再利用最小化準則來尋找最優解, 如(1)式中變分約束方程所示.并對其進行擴充, 修改為彈性網回歸, 則變分約束方程變為

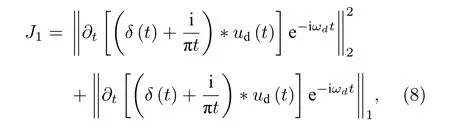
其中 ωd是第d個模態的中心頻率.

2) 殘余信號 fr(t) 與期望模態 ud(t) 的頻譜重疊應盡量小, 即在期望模態所在的頻帶內殘余信號的能量應盡量小.特別是 fr(t) 在 ωd處的能量應為零,以保證完全提取模態.

為了滿足這些約束條件, 首先通過合適的濾波器提取出屬于期望模態的 ud(t) 分量, 然后將濾波后的 fr(t) 的能量作為 fr(t) 和 ud(t) 譜重疊的指標.為此, 使用濾波器的頻率響應為

其中, β (t) 是所使用濾波器的脈沖響應.所以, 尋找期望模態的問題可以表示為一個(8)式和(10)式聯合約束的最小化問題:

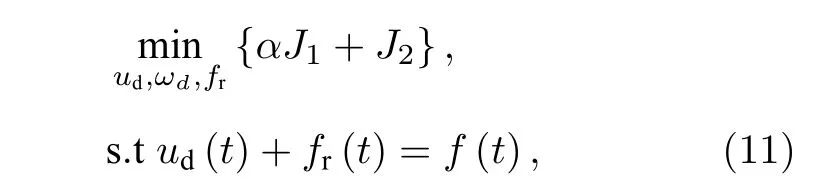
其中, α是平衡 J1和 J2的參數.

由(7)式—(11)式所推導出的變分約束模型,即是本文提出算法的理論模型.然后就可以按照2.1節中的ADMM迭代優化算法[19], 將上述變分約束求極值問題轉變成凸優化問題進行求解, 同時采用Parseval/Plancherel等距變換, 在頻域上寫出對應約束變分模型的增廣Lagrange方程:

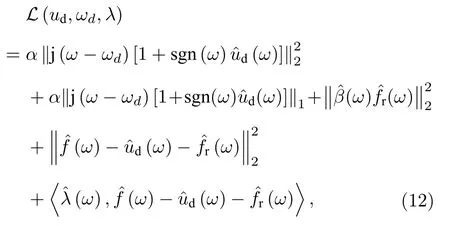
再按照文獻[19]中所提出的交替迭代方法, 該最小化問題可以通過一系列迭代優化來求解.即第(n + 1)次迭代所需模態函數可以表述為(13)式—(15)式.對(12)式求解以為變量時, (12)式的變分最小值問題, 解得:

同樣, 分別對(12)式求解關于 ωd和變分最小值問題, 可以得出:

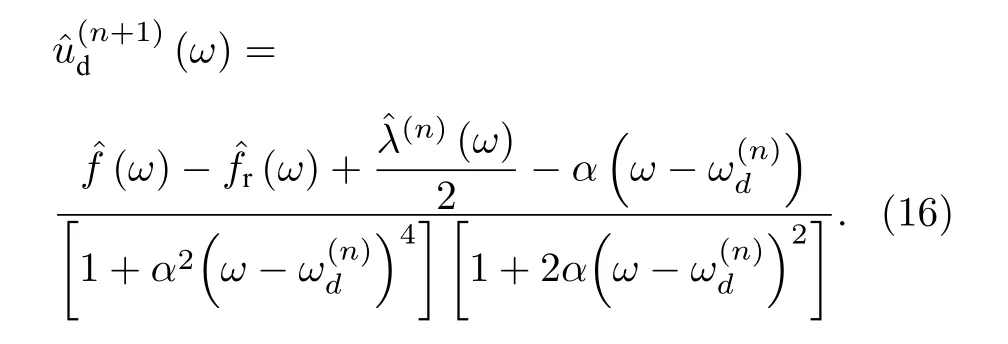
對(13)式進行相同的推導操作.在(13)式中,因為系數α取值很大, 分子處的第三項遠遠小于第一項.因此, 可以通過合理的近似對(13)式加以簡化, 忽略其分子中的第三個子項, ωd更新表達式可近似表示為

最后, 通過對偶上升法得到Lagrange乘子λ的迭代公式, 當濾波器中的系數 φ 取值與增廣Lagrange方程的懲罰因子α相等時, λ迭代公式得到最簡形式:

其中, η 是更新參數.綜上所述(16)式—(18)式即是本文提出算法的最終迭代公式.

至此, 彈性模態提取算法已經介紹完成, 算法流程如算法1所示.

算法1: EVME

repeat

n←n+1

更新 ωd:

對于所有 ω ≥0 進行對偶上升:

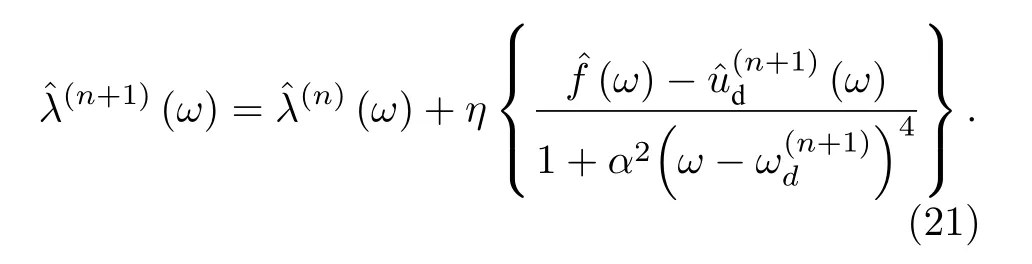
until 收斂:

3 實驗系統及測量結果

為了顯示本文所提出方法的準確性和有效性,搭建了時間相關單光子探測系統進行了實驗驗證.時間相關單光子探測系統工作原理如圖1所示, 信號發生器產生編碼脈沖信號驅動激光器, 同時產生計時信號輸入到TCSPC的計時通道2中作為計時參考.發射激光脈沖通過發射光路進行調節, 并經過掃描鏡照射到目標上.目標物體反射激光脈沖, 接收光路收集到回波信號, 通過光纖耦合輸入到單光子雪崩二極管(single photon avalanche photon diode, SPAD)中, 探測器將光信號轉換為數字信號輸入TCSPC的計時通道1中.最后對通道1和通道2的信號進行互相關計算, 可以計算出單個像素的距離.

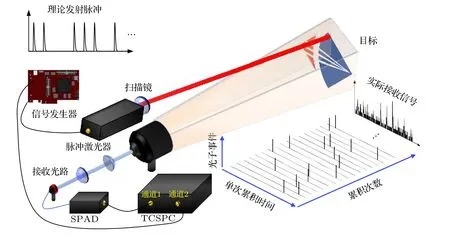
圖1 系統工作原理圖Fig.1.The principal components of the system.

實驗系統實物圖如圖2所示, 激光器型號為PicoQuant LDH-D-C-850, 波段為850 nm, 最大脈沖發射頻率為80 MHz, 平均功率為40 mW; TCSPC為PicoQuant PicoHarp 300, 最大時間分辨率為4 ps; 探測器是型號為EXCELITAS DTS_SPCMAQRH-16-FC的SPAD, 量子效率 > 40% @850 nm,暗計數率 < 20 cps; 采用型號為Xilinx KINTEX XC7 K325 T的現場可編程邏輯陣列(field programmable gate array, FPGA)作為信號發生器;二維掃描鏡型號為Thorlab GVS012; 帶通濾波片型號為Semrock FF01-850, 通過帶寬為 ± 10 nm.

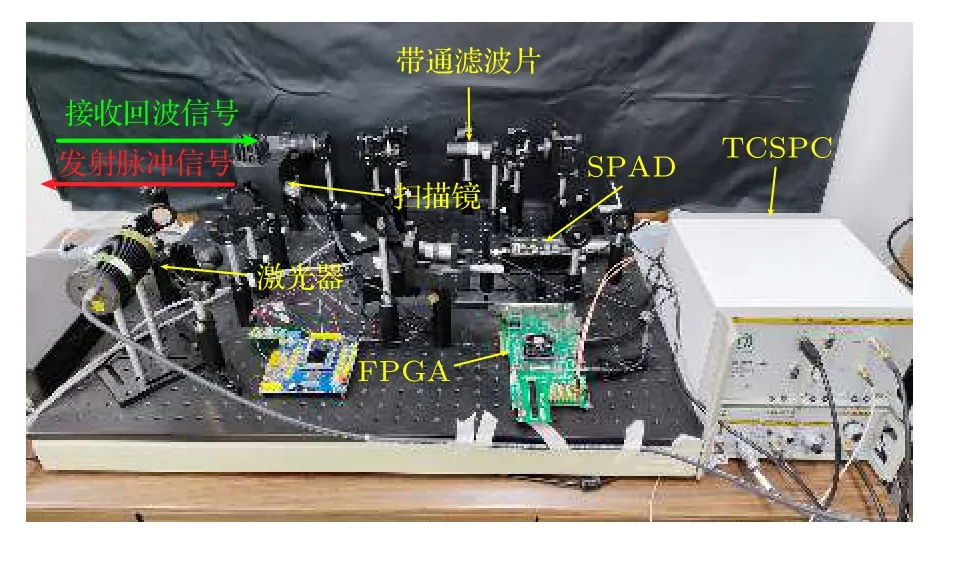
圖2 實驗系統實物圖Fig.2.Experimental system.

3.1 強噪聲條件下的信號去噪實驗

目標物體到接收光路物鏡的距離為7.3 m, 掃描鏡調整發射光束對準目標物體, 激光器實際輸出編碼脈沖頻率為1 MHz, 脈寬為500 ps, 平均發射功率為0.11 mW(由OPHIR PD300-3W-v1 & VEGA光功率計測量, 下同), 帶通濾波片用于濾掉除了850 nm以外的背景雜散光.為了模擬遠距離測試中的強衰減場景, 發射光路包含兩個型號為Thorlab NE30B-B的衰減片, 衰減倍數為4296.51倍,故系統平均發射功率為25.6 nW, 發射激光單個脈沖能量為25.6 fJ.而接收光路中SPAD探測器前放置了一個衰減倍數為380.99的衰減片, 型號為Thorlab NE40B-B, 可以通過激光雷達方程計算出此時目標物體到接收光路物鏡的等效距離約為3000 m.同時實驗在強噪聲場景進行, 接收光路物鏡處的850 nm波段背景噪聲平均功率實測為19.51 μW.所有數據是在基于Intel(R) Core(TM)i7-6700CPU和24GB 2133MHz DDR4的計算機平臺上測得的.

進行累積時長為5 s的探測, 截取部分TCSPC輸出探測信號段, 時間分辨率為16 ps, 截取的信號對應發射脈沖編碼為“1 1 0 0 1 1 1 0 1 0”, 如圖3(a)所示, 將其與經過不同算法處理后的信號進行對比.

圖3(a)理論發射信號由FPGA產生的實測輸出脈沖信號結合激光器出廠報告中給出的實測發射脈沖波形曲線計算生成.對比圖3(b)實際接收信號和圖3(a)理論發射信號, 可見本應有回波信號的地方, 由于系統發射平均發射功率為25.6 nW,此時接收光路物鏡處經過非協作目標物體漫反射的回波能量達到了10–18W量級, 遠遠小于實測850 nm波段背景噪聲平均功率19.51 μW, 這造成了大量的數據缺失, 無法重建出有效的信號波形圖, 導致信號失真.

圖3 時間相關單光子探測原始信號與6種方法對其重建的信號效果圖 (a)激光器理論發射光信號; (b)實際接收信號;(c) Hilbert包絡; (d) EMD; (e) CEEMDAN; (f) Haar小波軟閾值法; (g) VMD; (h)本文方法Fig.3.The curves of time-correlated single photon single-photon signal and its six reconstruction algorithms: (a) Original signal;(b) theoretical output signal; (c) Hilbert envelope; (d) EMD; (e) CEEMDAN; (f) Haar wavelet; (g) VMD; (h) proposed method.

對圖3(b)的實際接收信號進行Hilbert包絡重建, 結果如圖3(c)所示, 部分區域的噪聲能量密度和峰值已經超過了信號段的平均水平, 可見對實際接收信號采用基于峰值、半高全寬、包絡、能量密度、短時能量等常用信號特征提取手段無法直接提取出回波脈沖信號的準確位置信息.

圖3(d), (e)分別采用的EMD和CEEMDAN方法對圖3(b)信號進行處理, 均取分解后的本征模態函數1.將其與圖3(a)對比, 這兩種方法處理效果很差, 無法將信號與噪聲進行分離, 它們的信號特征相較于原始信號更差, 且隨著模態分解數量提升后, 模態混疊效果越嚴重.這是由于EMD和CEEMDAN方法都是利用信號自身統計特征, 在時域上對信號本身進行經驗分解.由于時間相關單光子計數技術所探測到的信號存在有效數據大量缺失、噪聲功率遠大于信號功率等問題, 造成信號自身的統計特征被破壞, 并不適用于這類以有效數據本身作為驅動的分解方法.

圖3(f)為采用Haar小波軟閾值(Haar wavlet,Haar WT)方法對原始信號進行重建的效果圖.將其與圖3(a)進行對比, 可見此方法僅在一定程度上提取出回波信號的位置, 但重建出的信號波形仍然受到泊松噪聲的影響, 重建出來的信號波形寬度不盡相同, 信號波形畸變程度大.

圖3(g)是基于VMD方法進行重建后取其本征模態函數1的效果圖, 模態分解數量為5.將其與圖3(a)進行對比, 可見此方法可以很好地提取出回波信號所在的位置, 但信號波形仍然存在明顯畸變, 信號波形的峰值隨機不固定.且模態分解數量需要多次實驗后確定.

圖3(h)為本文所提出的彈性變分模態提取方法的重建效果圖, 將其與圖3(a)進行對比.可以發現本方法不僅去除了泊松噪聲的影響, 在有效數據大量缺失的情況下依然可以提取出回波信號, 且每一個信號波形形狀基本相同, 畸變程度小, 信號峰值與圖3(a)中的理論峰值位置誤差在上述6種方法中最小.

為了進一步分析6種重建方法的重建效果, 采用均方根誤差(root mean square error, RMSE)、平均絕對值誤差(mean absolute error, MAE)和對稱平均絕對百分比誤差(symmetric mean absolute percentage error, SMAPE)這三種常用誤差評價指標來比較經這6種方法重建出來的信號和理論真值之間的誤差.這三種指標是信號處理領域廣泛使用的誤差評價指標, 用來衡量信號的重建質量, 例如在本領域文獻[14,15,25]中都有使用,因此本文采用這三種評價指標來量化上述6種重建方法的性能.計算公式見(23)式—(25)式.6種方法重建圖3(b)中的實際接收信號, 并以圖3(a)激光器理論發射光信號波形作為參考真值, 分別選取峰值、半高全寬、短時能量(計算公式為(26)式)三種信號特征作為信號位置判斷依據, 計算RMSE, MAE和SMAPE值, 結果見表1.

表1 6種方法重建信號性能分析Table 1.Performance comparison among proposed method and previously published methods.

均方根誤差計算公式為

平均絕對值誤差計算公式為

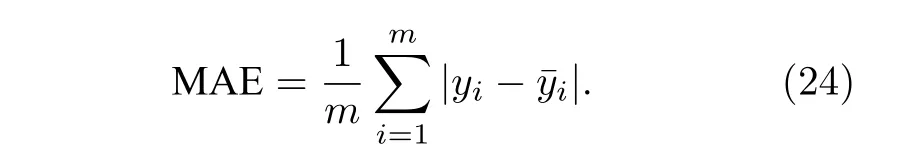
對稱平均絕對百分比誤差計算公式為

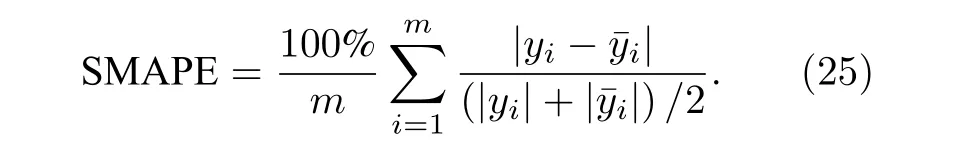
短時能量的計算公式為

其中, Ei代表第i個時間窗內的短時能量, s (·) 為輸入信號, w (·) 則為窗函數, l為窗函數的長度.窗函數一般取矩形窗, 公式如下:

由表1可見, 對于采用短時能量作為信號特征時, 在平均發射功率為25.6 nW、背景噪聲平均功率為19.51 μW的強噪聲條件下, 時間相關單光子計數信號重建精度的均方根誤差為1.414 ns, 對應到單個脈沖測距時, 其重建誤差為0.21 m; 而當采用脈沖偽隨機編碼方法時, 測距精度可提升至厘米級.與之相對的, 在文獻[1]中對天基非合作目標進行測距, 在激光脈沖重復頻率為200 Hz、功率為40 W、脈沖寬度為5.5 ns的條件下, 測距精度約為1.6 m.若采用本文去噪算法, 可以進一步提升測距精度.

3.2 不同累積時間下的信號實驗

為了進一步驗證本文提出方法的性能和普遍適應性, 在相同實驗環境下, 分別進行了不同累積時間下的實驗, 并采用上述6種方法對重建信號進行去噪, 進行比對.本實驗中, 調節發射光路衰減倍數為407.27倍, 故平均發射功率為270 nW, 單個脈沖發射能量的為270 fJ.接收光路物鏡處的850 nm波段背景噪聲平均功率為40.61 μW,SPAD探測器前放置了一個衰減倍數為380.99的衰減片, 型號為Thorlab NE40 B-B.采用3.1節中精度最高的短時能量信號特征作為信號位置判定依據, 采用RMSE作為衡量性能的指標.

由圖4可見, 本文提出的方法明顯優于其余5種方法, 其重建的時間相關單光子計數信號最為準確, 誤差最小, 其次為VMD, Haar WT, Hibert包絡, CEEMDAN, EMD.由于噪聲的功率遠大于有效信號的功率, 隨著累積時間的逐步增加, 噪聲信號的增量也會大于有效信號的增量.這6種算法達到一定累積時間后, 去噪效果均會達到極限, 其中Hibert包絡、CEEMDAN、EMD這三種方法即使達到了極限, 其隨機波動性依然很大.而采用本文方法進行重建, 隨著有效信號能量增強, 其重建信號誤差逐步減小至收斂, 隨機波動也逐步減小,當累積時間達到10 s時, 信號重建精度的RMSE誤差為0.408 ns.

圖4 6種方法在不同累積時間下去噪性能對比Fig.4.The line chart of the results comparison among proposed method and previously published methods.

表2給出了6種不同算法的計算耗時情況, 數據取自圖4中累積時長為10 s的實驗, 對應光子事件總數為17436個.

表2 本文方法耗時與其他方法的對比Table 2.Time consumption comparison among proposed method and previously published methods.

由表2可知, 本文提出的算法計算速度僅次于采用Hilbert包絡方法, 略優于Haar WT算法, 相較于VMD算法有了大幅度的提升, 這是由于本文方法在構建變分約束條件的時候, 僅僅在信號感興趣的中心頻率附近進行模態提取, 而不需要逐次迭代生成信號在所有頻段上的本征模態函數, 故而大幅度提升了計算速度.

4 結 論

本文分析了非平穩信號的特征, 深入研究了相關模態分解, 有針對性地在變分模態分解基礎上增加了相關約束條件, 從而能夠在指定中心頻率附近提取出有效信號, 并采用彈性網回歸來修改以Tikhonov正則化為基礎的不適定問題求解模型,提出了一種新的非平穩信號的時頻分解方法—彈性變分模態提取, 并給出其推導過程.經過理論分析與實測表明, 應用本文提出的方法對時間相關單光子計數信號進行去噪和特征提取, 在波段850 nm、系統平均發射功率為25 nW、背景噪聲平均功率為19.51 μW的條件下, 得到的重建信號與理論信號之間的均方根誤差為1.414 ns, 且不受模態混疊的影響.與現有VMD, EMD, CEEMDAN等特征提取方法相比, 本文提出的方法去噪性能更好, 特征提取精度更高, 運算速度更快; 能夠讓基于時間相關單光子計數技術的遠距離激光三維成像、非視域成像、水下目標探測等應用對復雜環境的適應性更強.