鋼材制造業中的鋼材切割下料問題

郭欣哲 王浩洋 劉崢 孫學峰 施金豆 李明壯

摘 要：在鋼材制造業中，針對鋼材切割下料的問題，提高原材料利用率是各個企業迫切需要解決的問題。本文通過對幾種版式不同的原材料進行切割，通過將其規整為1.5維問題，結合充分的線性約束，結合遺傳算法與蟻群算法的新式算法，建立數學模型，計算出最優的排樣方案，節省原材料，使其在理論價值和生活實際中具有重要作用，提高企業經濟效益。

關鍵詞：二維切割問題? 調度策略NP? 動態規劃? 線性約束? 新式啟發算法

中圖分類號：TG50? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼：A? ? ? ? ? ? ? ? ? 文章編號：1674-098X（2021）05（c）-0061-06

The problem of steel cutting in the steel manufacturing industry

GUO Xinzhe? WANG Haoyang? LIU Zheng? SUN Xuefeng? SHI Jindou? LI Mingzhuang

（Shenyang University of Aeronautics and Astronautics， Shenyang， Liaoning? Province， 110000? China）

Abstract： In the steel manufacturing industry， aiming at the problem of steel cutting and blanking， improving the utilization rate of raw materials is an urgent problem to be solved by various enterprises. In this paper， several raw materials with different formats are cut， which are regularized into 1.5-dimensional problems， combined with sufficient linear constraints， combined with the new algorithm of genetic algorithm and ant colony algorithm， a mathematical model is established to calculate the optimal layout scheme， save raw materials， make it play an important role in theoretical value and life practice， and improve the economic benefits of enterprises.

Key Words： Two-dimensional cutting problem; Scheduling strategy NP; Dynamic programming; Linear constraint; New heuristic algorithm

隨著社會生產力的不斷提高，生產規模不斷擴大，鋼材的原材料消耗量也隨之增加，但是由于鋼材價格的上漲，導致企業生產成本大幅上升，由此綜合利潤極劇下降，一些企業甚至出現虧損等情況。為了減輕企業壓力，當務之急是在鋼材切割下料生產環節有效提高鋼材利用率，節省鋼材，降低產品的生產成本。本文闡述的鋼結構產品排樣系統通過算法構建了一個排樣效率高、計算速度快和排樣效果好的方法，充分地提高了鋼材的利用率，減少余料剩余及廢料的數量，大大提高了企業的生產力與效益。

1? 問題分析

1.1 問題回顧

某鋼材生產制造商的鋼材切割流程。其中開卷上料環節將原材料鋼卷放在開卷機上，展開、放平送至右側操作區域剪切過程在剪切臺上完成，剪切臺上依次有切頭剪和圓盤剪。

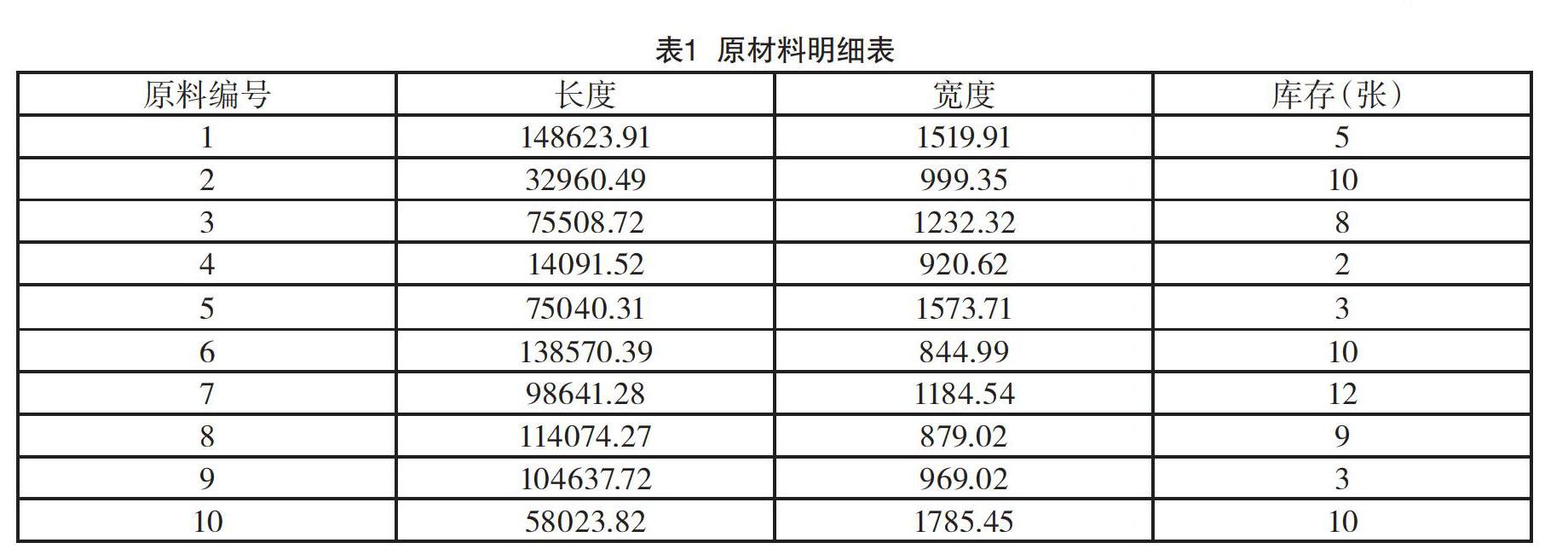
工廠未來一批訂單需求已給出，訂單需求數量必須恰好滿足（不允許超額供應）。根據工廠現有原料切割訂單，每種原料的使用數目不能超過其庫存，如表1、表2所示。

1.2 初步分析

本文研究的主要問題就是二維板材切割問題，其中夾雜著眾多約束。如表1所示，對于原料下料問題首先要確實采用那些合理的模式[1]。本題要求不允許超額供應，即為線性等式約束。其次根據題目要求的變量，將其數據化處理：排刀走刀限制、原料限制、余料限制等。可以將產品的長設為l，寬設為W，原料的長為L，寬為W，在研究面積的同時，把長度和寬度也作為兩個維度放入問題進行研究。但因為面積與長寬有乘積關系，所以可以近似看成2.5個維度。運用數學思想，找出每一個問題的所求函數關系，然后根據約束條件，分別添加到不同的問題中，主要運用遺傳算法，設置合理的參數進行模擬仿真下料，然后求解。

1.3 符號變量選取

符號變量如表3所示。

1.4 維切割模型的假設與建立

（1）假設切割過程無操作失誤導致原料浪費。

（2）假設無追加訂單。

（3）假設切割的鋼材全為合格品。

2? 數學模型

2.1 問題分析

一共有10種原料，在本問題中，考慮5種訂單。使用最少的原材料，將這些訂單合理排布在原料鋼材上，將問題數據化。

（1）目標函數：總原材料最少。

（2）適度函數：總的成材率最高。

（3）決策變量：使用的材料序號，不同訂單的序號，材料數目，訂單數目。

（4）約束條件：滿足板料的需求量（不能超額供應），材料庫存，排刀上限，余量標準。

2.2 蟻群算法和遺傳算法融合模型

遺傳算法是通過數學思維對達爾文生物進化論中的自然選擇和遺傳思想進行模擬的進化過程推演，是一種通過將自然進化的轉置到計算機上的過程搜索最優解的方法。該算法通過數學的方式，利用計算機模擬運算，將問題求解過程轉化為類似于生物進化中染色體基因交叉變異的過程。在求解復雜的組合優化問題時，與一些傳統的優化算法相比，通常可以快速獲得更好的優化結果。

遺傳算法的基本運算過程如下。

（1）重置：設置進化解析幾何電子計數器t=0，設置更大的進化解析幾何T，隨機生成M個個體作為原始種群P（0）。

（2）個體評論：計算組P（t）中每個個體的相關性。

（3）選擇計算：選擇算法應用于組。選擇的目的是將上升個體的基因立即遺傳給下一代或基于匹配交叉使新個體遺傳到下一代。選擇的實際操作是建立對群體中個體相關性的基本評估。

（4）交叉計算：交叉算法應用于種群。進化算法中的主導作用是交叉算法。

（5）變異運算：將變異算子作用于群體。即是對群體中的個體串的某些基因座上的基因值作變動。群體P（t）經過選擇、交叉、變異運算之后得到下一代群體P（t+1）。

（6）終止條件判斷：若t=T，則以進化過程中所得到的具有最大適應度個體作為最優解輸出，終止計算。

蟻群算法是一種用于尋找提升路徑的概率優化算法。這類優化算法具有普適計算、信息內容反饋調整和啟發式搜索的特點，它本質上是進化算法中的研究型全局蟻群算法。將粒子群算法應用于優化問題的理論基礎是：螞蟻的行走路徑用于表示待優化問題的可行解，所有螞蟻群的所有路徑構成了該室內空間。有待優化的問題。路徑較短的螞蟻會釋放大量的引誘劑。隨著時間的推移，在較短路徑上積累的引誘物濃度逐漸增加，選擇這條路徑的螞蟻數量也在增加。最后，所有螞蟻在反饋調整的作用下都會集中在最佳路徑上，此時的匹配就是待優化問題的最優解。

（1）采用正反饋機制，使得搜索過程不斷收斂，最終逼近最優解。

（2）每個個體可以通過釋放信息素來改變周圍的環境，且每個個體能夠感知周圍環境的實時變化，個體間通過環境進行間接的通訊[4]。

（3）啟發式算法擁有其獨特的概率搜索方式，很容易達到全局最優的情況。

遺傳算法雖然具有快速全局搜索能力，但是對于系統中的反饋信息卻沒有利用，往往導致無效的積冗迭代，求得的解往往不是最優解[2]，而蟻群算法是通過信息的積累收集和更新，來預測收斂最優路徑，但是算法開始階段信息匱乏，可使用信息較少，會導致算法速度變慢，前期準確性降低，誤差積累到后期會導致誤差較大[3]。通過將兩種算法融合，一方面克服了遺傳算法陷入局部最優解的情況，另一方面對照遺傳算法父代，減少蟻群算法的誤差，優勢互補，形成了一種時間效率準確性都比較好的啟發式算法[4]，并通過仿真模擬，進行計算二維切割問題。

2.3 MIN（原材料）數學模型

原材料消耗最少數學模型：

，

且為整數。

余料約束：

適額約束：

長度與寬度約束：

面積約束：

目標函數：

最優解存在，但干擾近似解也同樣很多。我們將數學模型代入Lingo，求得最優解如表4所示。

將得到的特解反向代入在MATLAB中構建的啟發式算法中，得到遺傳算法迭代圖和蟻群算法軌跡圖[5]。如下圖1、圖2所示。

由圖3可知，在遺傳算法100次迭代之后，目標函數優化曲線已經觸碰到最優值，但波動較大，在經過500次迭代之后，曲線的波動性減弱，漸漸平穩于最優解。在蟻群算法軌跡圖中，可以看出在經歷多次迭代之后，軌跡圖形成閉環，且路程最短，可以判定函數已經找到最優解。將從Lingo得出的答案代入啟發式算法函數，結果滿足約束條件，且全局最優。

2.4 二維矩件排樣模型

工廠加工要求使用圓盤剪前，需根據訂單切割方案進行排刀。假設排刀架上可以以任意間距排刀，但刀具數量是有限制的，一次排刀上限不能超過5刀。用同一排刀方案切割得到的訂單稱為一組訂單，切割不同組時需要工人重新排刀，稱為一次換刀。切割每卷原材料之間均需要換刀[6]。切頭剪為“一刀切”，即將整個鋼板橫向完全切斷。經過橫向切割后，當且僅當某些訂單還需要額外橫向一刀將其與廢料分開，則將這些訂單移至小機器再次切割[7]。同一組內相同訂單可以通過一刀同時變成成品。鋼材切割訂單有兩種，分別是板料訂單和卷料訂單，切完的板料訂單直接通過下料小車包裝入庫[8]。

運用遺傳算法，將在Lingo中求得的數據進行排樣，然后直接進行優化處理。遺傳算法設計如下。

（1）編碼：采用十進制整數編碼方式。

（2）適應度函數：將適應度函數定義為f? = Area / Area1，其中，Area是待排入矩形零件的面積總和，Area1是所得排樣圖高度輪廓線以下的矩形板材面積。

（3）初始種群：使用隨機函數來生成一定數量的十進制整數序列組成父輩群體，設定種群規模 M=50。

（4）交叉算子：采用單點交叉和雙點交叉設置交叉概率pc=1，單點交叉與雙點交叉各占一半。

（5）變異算子：采用位置變異和旋轉變異設置位置變異概率pm1=0.1和旋轉變異概率pm2=0.1。

（6）選擇算子：根據適應度函數值從大到小排列執行完交叉、變異操作的個體，選擇前M個個體組成下一代父輩群體。

（7）結束條件：設置迭代多少代，設置maxgen = 500。

針對矩形板材排樣問題，建立了整數規劃模型，利用Lingo，給出了多種限制的條件下的最優排樣方案。通過軟件計算，需要切割的訂單的總面積為s=2336.8，原材料面積S=2715.6m2。

目標函數為零件面積所占板材面積最大：

約束條件：

對于上述線性規劃，結合已求的原材料數量，利用Lingo軟件求解，得到了最優排樣方案，如表5所示。

2.5 切割方案

得到具體切割方案，如表6所示。

3? 結語

（1）通過利用數學工具和各種編程軟件，嚴格地對模型進行求解，具有科學性。

（2）本文針對矩形鋼材地優化排版切割問題，建立了在不同限制條件下地約束方程，得到了可以解題地各個優化模型，通俗易懂，且在保證使用最少原材料地基礎上，同時擁有較高地成材率，模型可以推廣到其他二維切割領域使用。

（3）同時對于可行解較多的模型計算，采用了不同的數學工具，大大減少計算時間，利用遺傳算法和蟻群算法的啟發式算法對計算過程和計算結果進行優化，得到了模型的最優解，使模型的可操作性提高。

（4）本文數學模型建立在原材料供應充足，并且完全切割的情況。但是在實際生產生活中，原材料供給不足，刀具損毀等多種情況發生，影響企業效益，那么在這種情況下如何改變參數和約束條件是今后研究的方向。

（5）本文研究并解決了一些特殊的切割問題，即1.5維切割問題。不僅把切割材料的長和寬作為思考方向，而且加入了面積因素。同時因為面積被材料的長和寬所限制，所以把面積以一個0.5維度放入問題進行考慮。針對其特殊性，采用蟻群和遺傳算法進行求解。計算結果表明，該新式混合算法對解決1.5維問題行之有效。其次對于可進一步減小切割損耗的切割路徑優化問題進行討論。通過對比切割路徑優化問題和旅行商問題，這雙方之間有很多共同之處，最終采用遺傳算法求解。最后為了進一步減少浪費，對排樣切割所剩下的廢料采取進一步的優化措施。經過一次切割之后，由于所剩廢料的數量和大小都不同，因此針對這些余料可建立二維切割矩形模型，解法同上。

參考文獻

[1] 熊慧，黃菊永.基于貪心啟發式算法的多目標二維切割問題[J].電子技術與軟件工程，2016（24）：154-155.

[2] 丁建立，陳增強，袁著祉.遺傳算法與螞蟻算法融合的馬爾可夫收斂性分析[J].自動化學報，2004，30（4）： 629-634.

[3] 李淑芳.數控切割下料誤差產生的原因及應對策略[J].自動化應用，2018（10）：155-156.

[4] 武小年，奚玉昂，張潤蓮.DEM中基于遺傳與蟻群的混合路徑規劃算法[J].計算機應用研究，2020，37（9）： 2694-2697.

[5] 李明.基于特征粒子算法的云資源調度策略研究[J].計算機與數字工程，2016，44（2）：307-310，342.

[6] 姚奕，鄭瀟，張文聰，等.重工鋼材智能切割管控系統軟件設計[J].電子技術與軟件工程，2021（8）：83-84.

[7] 張衡.基于二維平面裝箱模型的產品切割問題研究[J].運籌與模糊學，2019，9（4）：249-263.

[8] 何雙池，陳學松.二維矩形件排樣的切割式填充算法[J].數學的實踐與認識，2019，49（18）：132-139.