水下航行器極區內對準以及格網導航技術

迪玉茹，黃海，阮衛

(中國船舶集團有限公司 第七〇五研究所，陜西 西安 710077)

0 引言

極區是地球球體的兩端，臨近地理極的區域，是地理緯度最高的區域。隨著世界各大國間經濟互通、航運交往的頻繁，跨越極區的航路越來越受到重視，極區的軍事、經濟、自然資源等戰略意義及重要性越發凸顯。目前，各國在極區的科研活動都在加強。

極區內水下對準及導航技術的研究，可使水下航行器具備全球導航能力，為實現極區內經濟和軍事戰略提供理論支撐和技術儲備。因此有必要開展水下航行器在極區內的導航及對準技術研究與關鍵技術探索，深入研究適應極區環境的對準和導航策略。

水下航行器主要采用慣性導航。針對水下航行器慣性導航系統在極地的使用，存在的問題主要有以下幾點[1–6]：

1）航向角定義失效

在水下航行器導航計算中，通常采用的是地理坐標系實現在地球表面的導航。根據航向角定義，航行器縱軸水平面投影與北向的夾角為航向角，而在極地附近，原本是一條指向線的“北向”變成一個點，航向角失去定義。

2）經典慣性導航力學編排失效問題

在經典慣性導航力學編排中，存在對地球自轉角速率的跟蹤指令。在高緯度地區，天向指令將趨于無效。這與傳統的指北方位平臺慣導力學編排在高緯度地區存在計算溢出和方位陀螺施矩困難的問題是一致的。

3）航向角無法提取

在極地附近，當航行器穿過極地附近（例如經度由0°直線駛向180°，10°駛向190°等），航向角速度未發生變換，而航向角卻將發生180°跳變，慣導解算無法提取。

4）初始對準算法失效

與非極區相比，極區存在的經線收斂問題會導致常規的基于地理北向方向參考線的導航算法失效，與之相應的主慣導對子慣導系統的傳遞對準算法也將失效。必須通過分析其導航誤差模型，建立適應極區內傳遞對準的卡爾曼濾波算法。

5）定位計算失效

在極地附近，由于地理緯度接近±90°，當有定位計算要求時，經度解算中存在除緯度余弦的算法，定位計算提取誤差很大。

針對上述水下航行器極區導航存在的問題，本文提出一種利用格網坐標系直接獲得格網航向，進而優化慣導系統導航性能的方法，研究格網慣性導航算法編排方案，以滿足水下航行器在極區航行時的導航需要。同時，對格網慣性導航的誤差進行建模，并據此設計格網導航系統的“速度匹配”傳遞對準算法，利用卡爾曼濾波器，實現對子慣導誤差的估計和校正。

1 極區格網慣性導航編排

1.1 格網坐標系

格網導航坐標系G與地理坐標系e和地球坐標系e間的相互關系如圖1 所示。以載體所在地P點處平行于格林威治子午面的平面作為格網平面，載體所在地的水平面作為切平面，格網平面與切平面的交線定義為格網北向，格網天向同地理天向重合，格網東向在切平面內且與格網北向垂直構成右手直角坐標系，即為格網坐標系。格網北向同真北方向的夾角為 σ，三軸單位向量集記為 (eGE,eGN,eGU)。

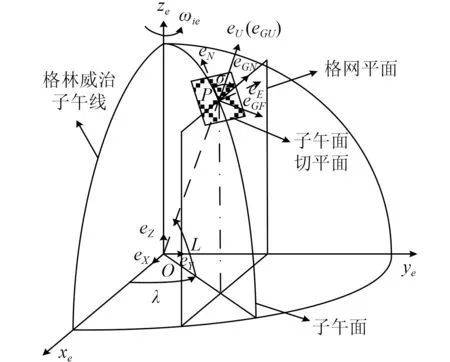
圖1 格網坐標系Fig.1 Grid coordinate system

根據格網坐標系定義，地理和格網坐標系間的轉換關系為：

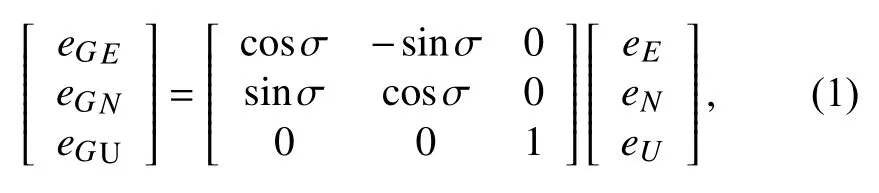
即由地理坐標系到格網坐標系的方向余弦矩陣為：

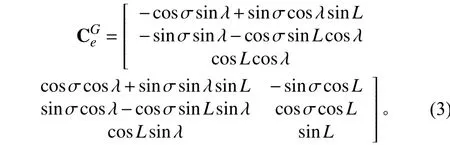
由此可得：

將sinσ，cosσ代入式（3）得：

1.2 格網導航力學編排

格網導航坐標系內的慣導力學編排同游移方位慣導系統有許多相同的地方，在計算指令角速度的時候略有不同。選取格網坐標系G為導航坐標系，則有：

1）姿態更新微分方程

其中：

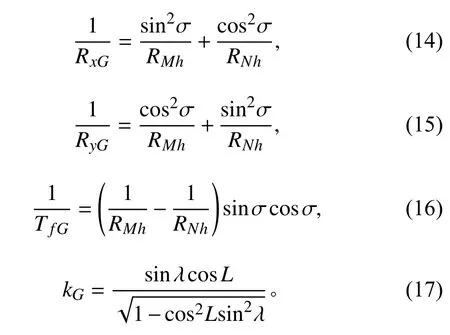
2）速度微分方程

參照文獻[1–5]比力方程，可類推出格網導航坐標系下的比力方程：

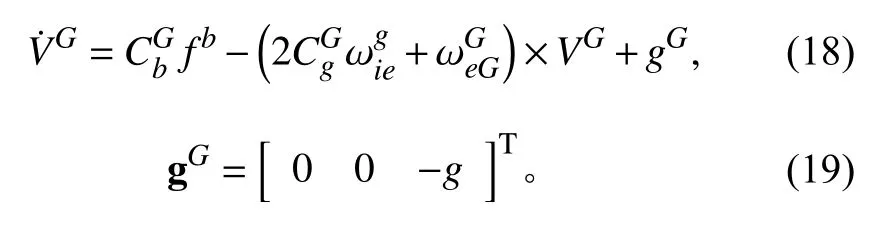
3）位置微分方程

指北方位慣導力學編排和游移方位慣導力學編排的位置求解都是通過位置方向余弦矩陣微分方程的數值積分獲得經緯高定位信息，而在高緯度地區采用經緯高的定位策略不再適用，此處采用ECEF 坐標表示航行器的實時位置R(x,y,z)：

由地球坐標和直角坐標間關系可得：

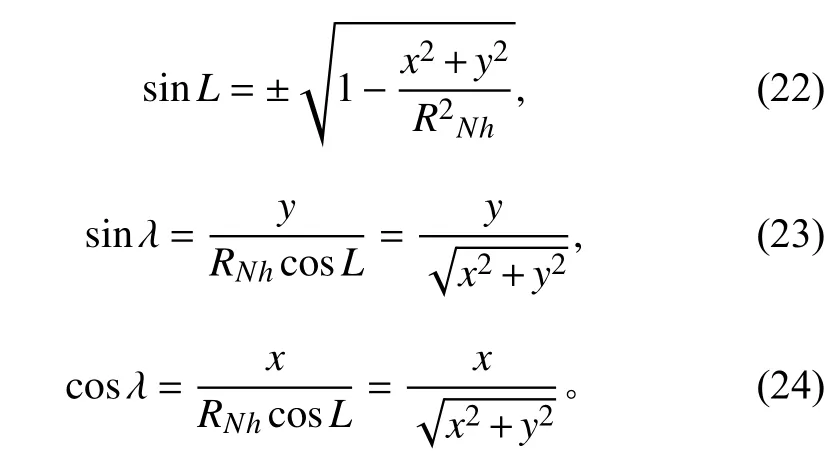
式（22）中當L為北半球時L取正號，南半球時L取負號。

2 極區格網速度匹配對準算法

2.1 格網慣性導航誤差建模

1.2 節是完整的格網導航力學編排形式，是在地球為橢球模型的基礎上推導的。為簡化分析，在推導格網導航誤差方程的過程中假設地球是圓球模型。考察完整格網導航力學編排方程可知式（13）是與地球模型相關的，在圓球模型下位置速率可用如下簡化式計算：

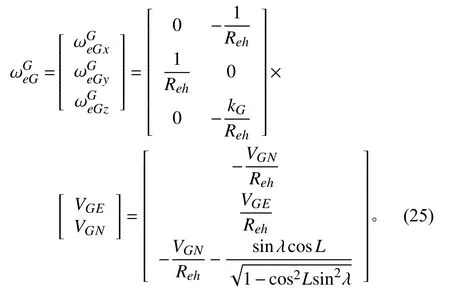
相應的由式（20）計算的直角坐標位置R(x,y,z)計算經緯高時也可作簡化處理。

則格網慣性導航的速度誤差方程：

姿態誤差方程：

位置誤差方程：

另外將陀螺漂移 εb、加速度計偏置 ?b視為隨機常值和隨機白噪聲的和：

其中：

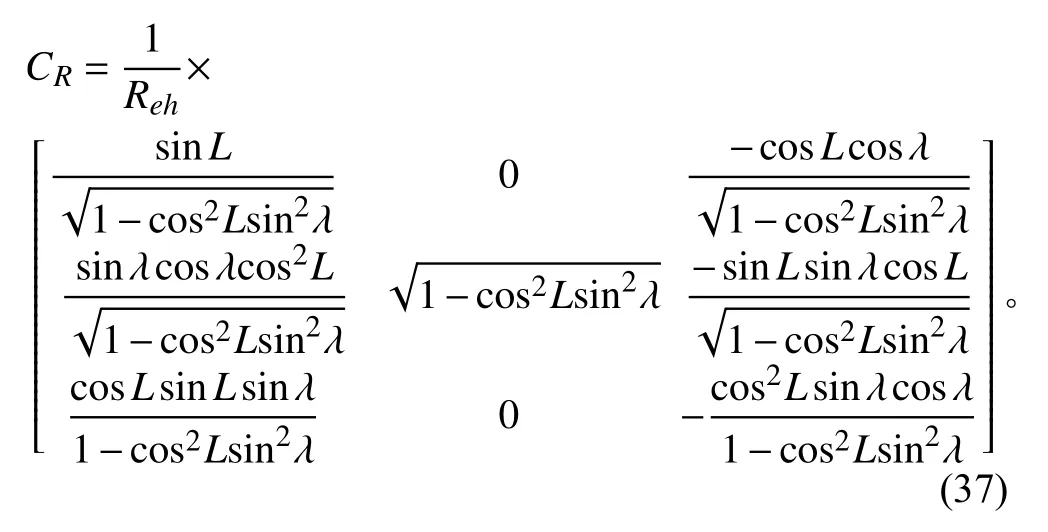
2.2 格網導航“速度匹配”傳遞對準算法

取子慣導姿態誤差 φG、速度誤差δVG、ECEF 位置誤差 δRe、陀螺漂移 εb和加速度計零偏 ?b為狀態變量，即

選取主慣導速度輸出與子慣導速度之差作為量測量，即

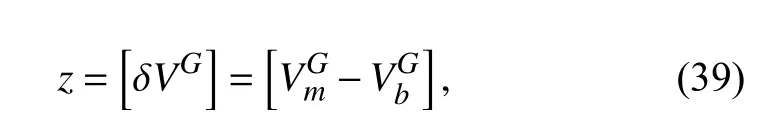
則量測方程為：

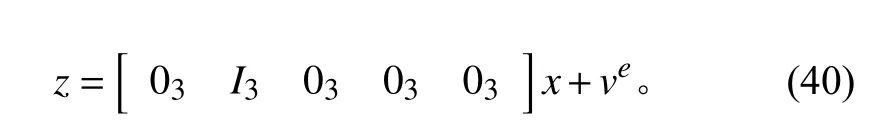
式（33）組成了“速度匹配”傳遞對準算法的卡爾曼濾波模型。

3 仿真分析

3.1 格網導航有效性驗證

為了驗證極區格網導航算法的有效性，仿真生成一條沿著某條固定的經線穿越極點然后駛出極區的軌跡。

仿真過程具體仿真參數設置如下：

1）軌跡起始點[89.7°N 108°E 300 m]；

2）航行速度和時間為沿著108°E 經線以50 m/s 速度向極點航行，穿越極點后沿著72°W 駛離極點，共航行1 000 s；

3）慣性器件誤差為陀螺隨機常值漂移0.01°/h ；加速度計隨機常值偏置40 ug。

整個航行過程航行器無航向機動，航行軌跡在地球上如圖2 所示，整個軌跡過程的位置真值如圖3 所示。

圖2 極區導航仿真軌跡Fig.2 Simulation track for polar navigation

圖3 極區導航仿真軌跡真實經緯高Fig.3 Real longitude and latitude of simulation track for polar navigation

東北天坐標系編排下姿態角誤差、速度誤差和位置誤差如圖4～圖6 所示。

圖4 東北天坐標系下姿態角誤差Fig.4 Attitude errors of ENU coordinate system

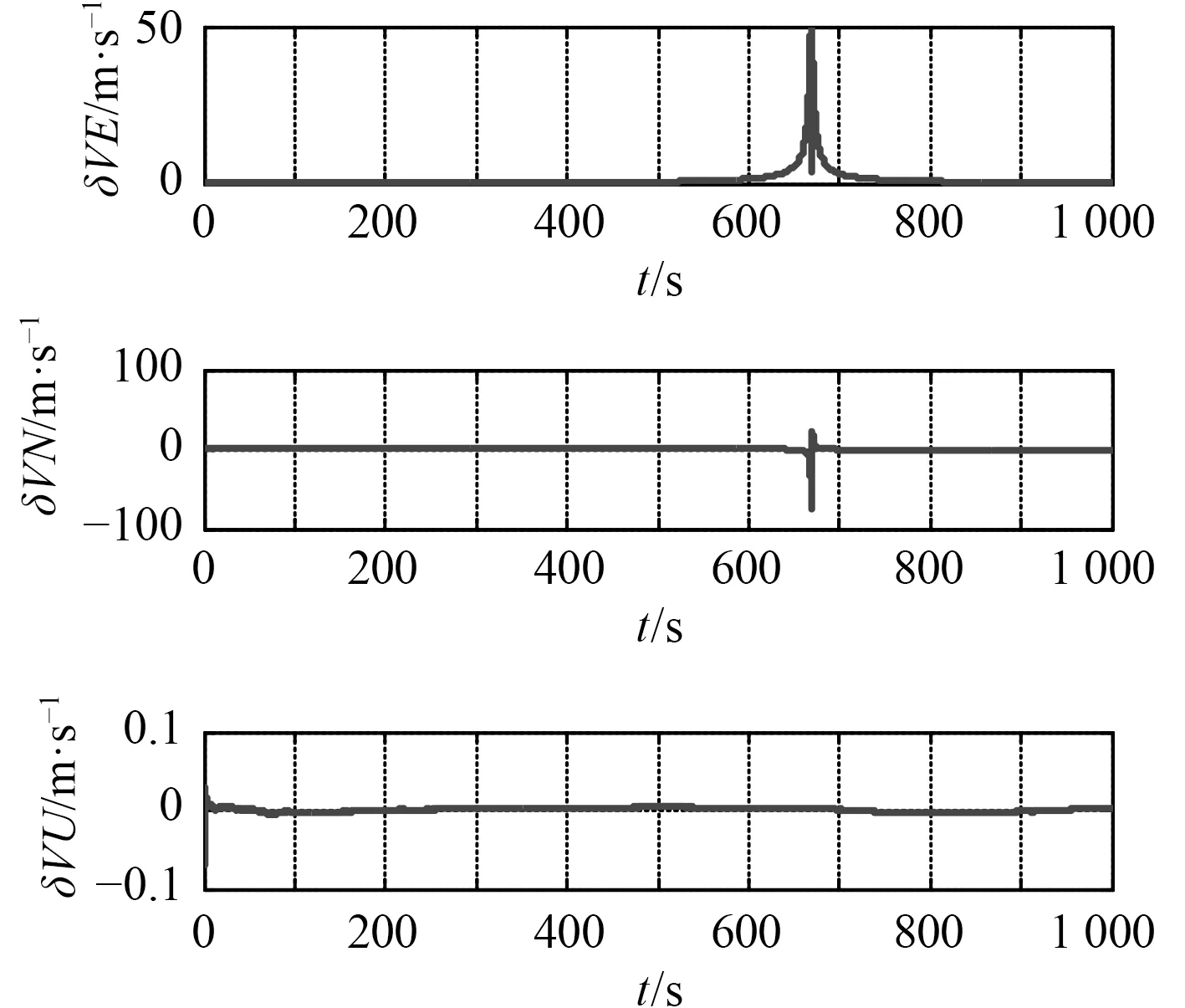
圖5 東北天坐標系下速度誤差Fig.5 Velocity errors of ENU coordinate system

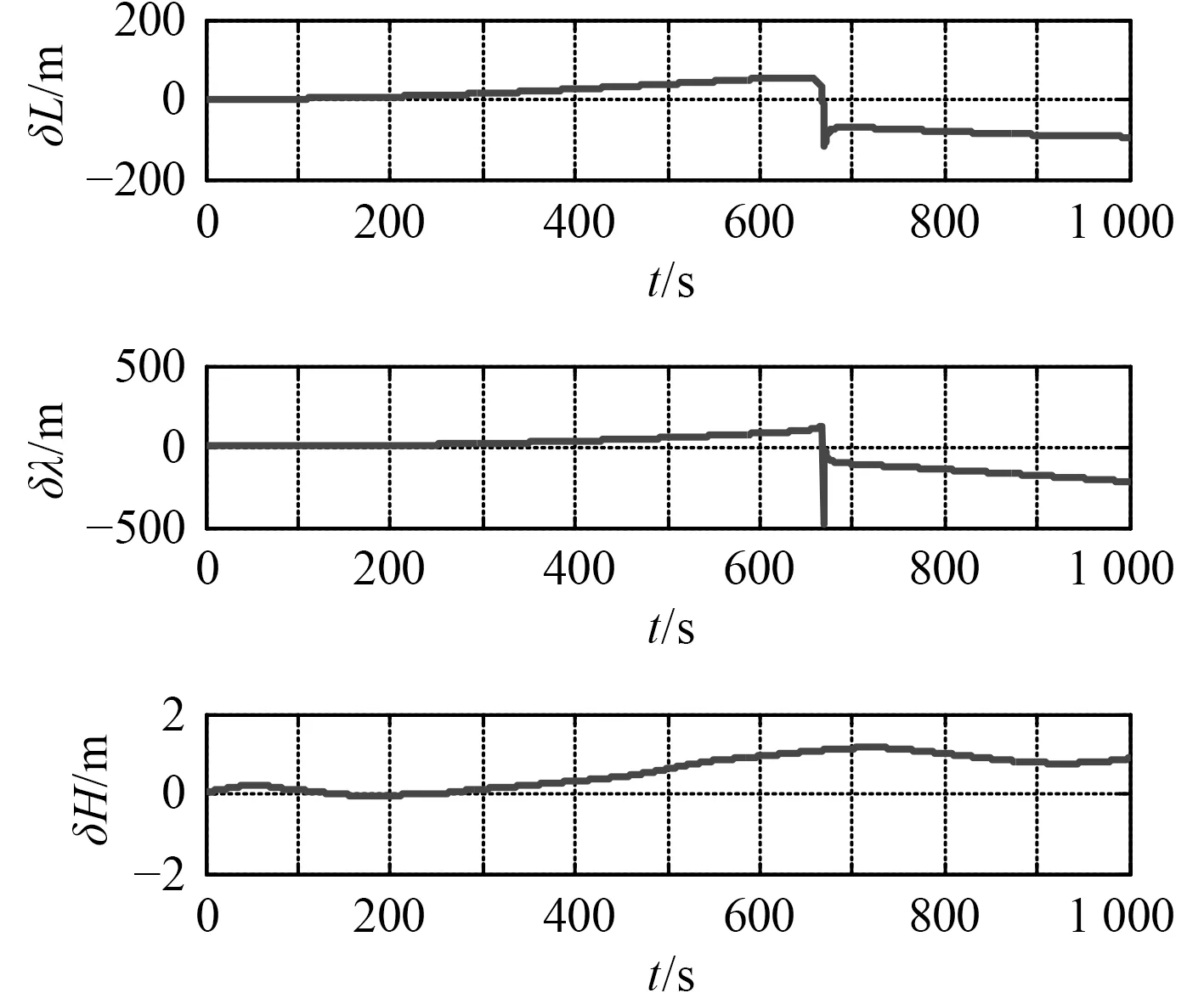
圖6 經緯高位置誤差Fig.6 The errors of longitude and latitude

格網導航解算下姿態角誤差、速度誤差和位置誤差如圖7～圖9 所示。

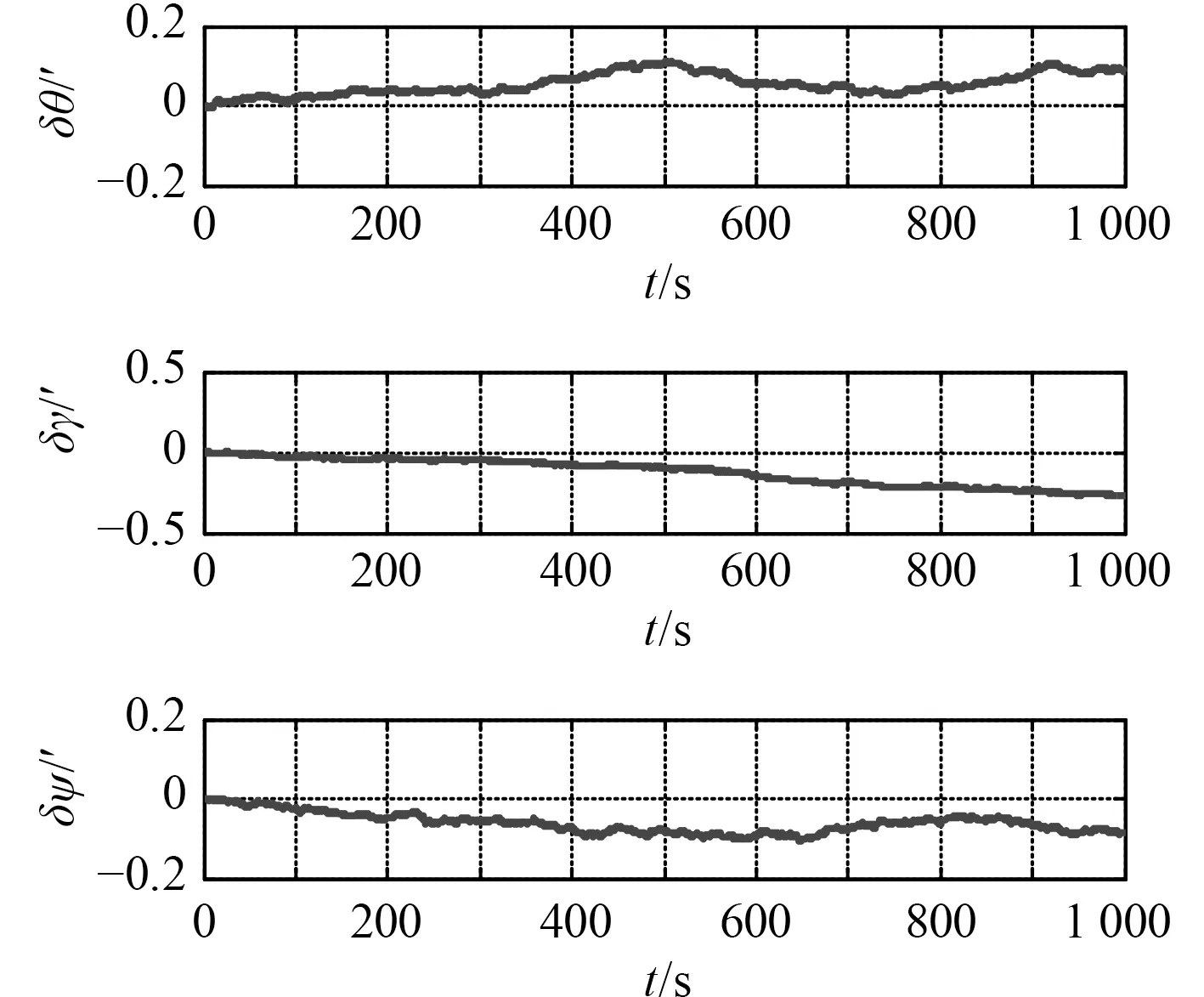
圖7 格網坐標系下姿態角誤差Fig.7 Attitude errors of grid coordinate system

圖8 格網坐標系下速度誤差Fig.8 Velocity error of grid coordinate system

圖9 ECEF 坐標系下位置誤差Fig.9 The error of position in ECEF coordinates

由圖7～圖9 可以看出，格網導航在15 min 內由慣性器件誤差引起的水平姿態角誤差小于0.5′，方位失準角誤差小于0.2′，水平速度誤差小于0.5 m/s，圖8所示水平位置誤差小于200 m。

圖4～圖6 中，傳統慣導解算方法下姿態角誤差、速度誤差以及經緯度誤差在極點附近存在跳變。因此，在極區不適合采用經緯度作為定位輸出參數，而應輸出地心地固坐標下位置參數。

3.2 “速度匹配”傳遞對準算法有效性驗證

對上述提出的“速度匹配”傳遞對準算法進行仿真驗證，仿真參數設置及仿真軌跡如下：

1）慣性器件誤差設置

陀螺儀：常值漂移0.01o/h，隨機游走系數為刻度系數誤差30 pp√m；加速度計：常值零偏5×10?5g，隨機游走系數刻度系數誤差40 ppm。

2）慣導初始誤差

3）導航解算周期為0.01 s，仿真時間100 s。

4）卡爾曼濾波器參數

狀態估計初值設置為0，初始方差陣取為真實均方誤差陣的5 倍，卡爾曼濾波周期取為0.01 s，速度量測噪聲0.1 m/s。

設置2 種航行軌跡：勻速直航、加速直航。航行器以30 m/s的初始速度勻速航行，如表1 所示。

表1 航行軌跡設置Tab.1 Setting of torpedo track

分別在2 種軌跡下進行仿真，失準角估計誤差如圖10 和圖11 所示。

由圖10 和圖11 可得，采用“速度匹配”傳遞對準算法，速度誤差與慣導水平失準角直接相關，因此該對準方法水平失準角的收斂速度相對較快，當航行器勻速直航時，水平失準角在10 s內即可收斂到1.5′以內，而方位失準角無估計效果。當航行器加速直航時30 s 內方位對準精度在4′以內，驗證了加速對方位失準角的激勵作用。

圖10 勻速直航下失準角估計誤差Fig.10 The estimate error of misalignment angle in direct navigation and uniform speed

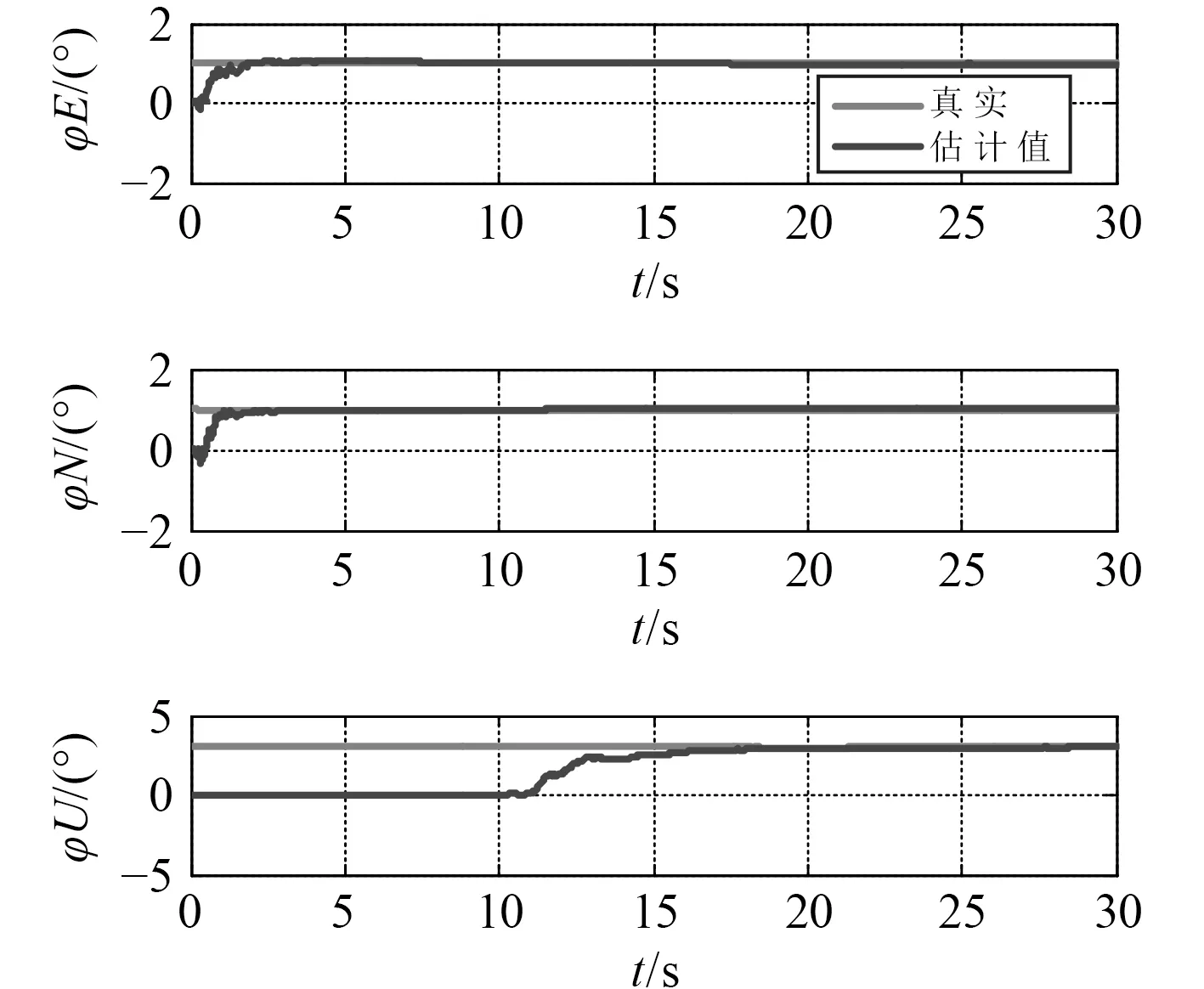
圖11 加速直航下失準角估計誤差Fig.11 The estimate error of misalignment angle in direct navigation and acceleration

4 結語

本文針對水下航行器慣導系統在極區因地理經線快速收斂導致無法精確定位定向的問題，提出一種利用格網坐標系直接獲得格網航向，進而優化慣導系統導航性能的方法，研究了格網慣性導航算法編排方案，以滿足水下航行器在極區航行時的導航需要。仿真結果表明，在格網慣性導航下，采用高精度慣性器件，15 min 內水平姿態角誤差小于0.5′，方位姿態角誤差小于0.2′，水平速度誤差小于0.5m/s，ECEF 坐標系下的位置誤差全程小于200 m。

針對水下航行器在極區內的對準問題，對格網慣性導航的誤差進行建模，并據此設計了格網慣導系統的“速度匹配”傳遞對準算法，利用卡爾曼濾波器，實現對子慣導誤差的估計和校正。仿真結果表明，采用該傳遞對準算法，水平失準角在10 s 內即可收斂到1.5′以內，同時，加速機動對方位失準角有激勵作用，30 s 內方位對準精度在4′以內。