快速路入口匝道控制策略綜述

葛靜 張麗巖 馬健

摘? 要：隨著城市規模的逐步擴大，機動車保有量和交通需求都有了明顯增長，各種交通問題逐漸涌現出來。在眾多問題中，日益嚴重的交通擁堵是各城市發展共同面臨的社會問題，其中快速路的堵塞尤為嚴重。因此，如何通過實施合理的控制措施來緩解快速路交通擁堵，成為當前研究的重點，在眾多的快速路交通控制策略中，匝道控制相關的研究較多，取得的效果也較好。本研究重點介紹了快速路入口匝道控制，根據對交通信息反應的區別可將入口匝道控制策略分為靜態控制和動態感應控制;根據控制區域的范圍將其分為單點控制和協調控制。最后在總結現有匝道控制策略的基礎上，對未來的快速路匝道控制策略的研究方向進行了展望。

關鍵詞：快速路;入口匝道;控制策略

中圖分類號：F570? ? 文獻標識碼：A

Abstract： With the gradual expansion of the scale of the city， the number of motor vehicles and traffic demand have increased significantly. All kinds of traffic problems emerge gradually. Among many problems， increasingly serious traffic congestion is a common social problem in the development of cities， especially the expressway congestion. Therefore， how to alleviate the traffic congestion of expressway by reasonable control measures has become the focus of the current research. Among the many expressway traffic control strategies， there are more researches on ramp control and better results. This study focuses on the on ramp control of expressway， which can be divided into static control and dynamic induction control according to the different responses to traffic information; according to the scope of control area， it can be divided into single point control and coordinated control. Finally， on the basis of summarizing the existing ramp control strategies， it looks forward to the future research direction of expressway ramp control strategies.

Key words： expressway; on ramp; control strategy

0? 引? 言

作為城市道路交通網絡的骨干，快速路因其特點吸引交通流量日益增加，這極大地緩解了交通運輸的壓力，提高了城市的服務水平。然而由于缺乏合理的控制和有效的引導，快速路的安全和擁堵問題日益嚴峻，具體表現為高峰時期堵塞嚴重、車流運行速度緩慢、尾氣排放加大等。這些問題導致快速路通行能力下降，安全風險增加，逐漸失去其優勢，因此快速路交通主動控制是當前交通管理部門的研究重點。根據以往的經驗，匝道控制是當前應用最為廣泛可靠的方法，匝道控制的范圍包括入口匝道和出口匝道，本研究將重點分析入口匝道的控制策略。

1? 入口匝道控制策略分類

1.1? 匝道關閉

匝道關閉就是通過采用人工護欄或放置交通禁行標志等方式，將部分入口匝道在某些特殊情況下進行暫時或永久性關閉。采用匝道關閉可有效解決因匝道問題帶來的道路交通壓力，增加快速路匝道合流區通行能力，緩解主線擁擠。但采用此方法大大增加了關聯道路的交通流量以及車輛總行程時間，易引起出行者的異議，因此匝道關閉一般只在以下等特殊情況下采用：

（1）極端天氣情況下易發生交通事故，此時可關閉入口匝道;

（2）當快速路發生事故等意外而造成路段瓶頸時，為防止交通狀況進一步惡化可關閉入口匝道;

（3）當快速路系統已達飽和，再增加車輛易引起大面積堵塞，且附近有良好的繞道行駛路線時，可暫時關閉入口匝道。

1.2? 入口匝道控制

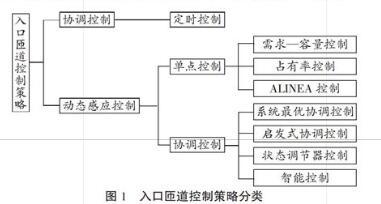
半個多世紀以來，國內外的學者始終致力于匝道控制算法的研究，提出了各種新的匝道控制策略，根據對交通信息反應的區別可分為靜態控制和動態感應控制;根據控制區域的范圍可分為單點控制和協調控制。匝道靜態控制以

Wattleworth提出的定時控制為主，因此本文將入口匝道控制策略分為：定時控制、單點感應控制和協調感應控制，其分類具體情況如圖1所示。

2? 快速路入口匝道控制算法

2.1? 定時控制

定時控制即假設某一時段的交通流運行狀況以及控制周期和相位是近乎固定的，根據歷史數據提前確定匝道控制率，常用方法是通過匝道信號燈進行匝道車輛的控制。該算法以匝道匯入主線的流量最大為目標，以快速路實際通行能力為約束，即匝道調節率r是由上游交通需求q、下游通行能力q和匝道期望匯入主線交通量q的關系來決定。當q≥q+q時，不會發生擁堵，因此不需要控制;當qq時，無法通過匝道控制消除擁堵，可暫時關閉入口匝道，并盡量降低上游交通需求。

這種控制方法模型計算比較簡單，但是只適用于交通流變化不大的路段以及10～30min的控制周期，一般可在交通流量有明顯增加時使用。當交通流波動較大時，其控制效果十分有限，無法對實時交通變化和突發性擁擠做出相應處理，很難放到具體工程應用中。針對定時控制存在的不足，國內外學者從改進其目標函數或模型等多個角度對其進行了優化。Papageorgiou在充分考慮快速路入口匝道流量的變化以及其對下游影響的基礎上，提出了快速路動態交通模型控制算法，可在較長的快速路實施控制，同時他還提出了分時段線性規劃（Linear Programming ， LP）控制方法。楊曉光則探究了快速路通行能力、車流運行速度以及出、入口匝道車流的排隊約束，對傳統LP控制算法進行優化，提出了動態LP控制算法[1]。

2.2? 匝道單點控制

匝道單點控制的目的是改善該匝道的交通狀況，常用方法有需求—容量控制（The Demand-Capacity Strategy）、占有率控制（The Occupancy Strategy）和ALINEA控制。

2.2.1? 需求—容量控制

1975年，Masher提出了需求—容量控制[2]，該方法中匝道調節率的確定也是通過比較q和q的關系得到的，目的是保證主線下游交通量在快速路通行能力范圍內并最大化其利用率，算法具體描述如下：

rk=? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（1）

式中：rk為第k個控制時段的匝道調節率;r為最小調節率;qk-1為第k-1個控制時段主線上游交通量（veh/h）;Ok-1為第k-1個控制時段主線下游占有率;O為臨界占有率。

2.2.2? 占有率控制

以需求—容量控制的研究為基礎，Masher又提出了占有率控制，他利用檢測器實時獲取主線上游和下游的占有率，并通過經驗公式估計下游流量來確定rk。當下游通行能力為負時，采取最小調節率，否則需通過公式估算，即：

rk=? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（2）

式中：v為自由流速度（km/h）;g為調節參數，取決于檢測器及車輛長度。

上述兩種方法都屬于開環控制，對外部干擾敏感度較高，但由于缺乏反饋機制，系統的穩定性相對較差。

2.2.3? ALINEA控制

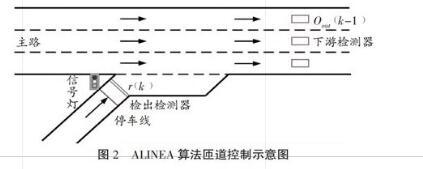
為了解決開環控制算法存在的問題，Papageorgiou等（1991）提出了一種局部交通反饋控制算法——ALINEA（Asservissement line'aire d'entre'e autoroutie're）[3]。與前兩種控制方法不同的是，ALINEA是閉環反饋控制，它以經典自動控制理論作為算法基礎，采用該算法時具體檢測器布設示意圖如圖2所示，其具體控制過程為：在快速路匝道下游約40m處安裝檢測器以檢測下游實時占有率，通過比較實時占有率與預先設定的下游期望占有率來確定匝道調節率，匝道車流的匯入通過信號燈控制，從而保證主線下游的車輛運行處于理想狀態。同時該方法還考慮了上一控制周期的調節率，可以避免本周期的匝道調節率出現較大的波動，保證車流的平穩運行。

ALINEA算法的基本模型為：

rk=rk-1+K-Ok-1? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（3）

式中：K調節參數;為主線下游期望占有率。

上式在經典自動控制理論中被稱為I型（積分）調節器，可以看出當交通流在相鄰時段變化不大時，如匝道上游交通量q為常數或變化很小，此時該調節器會自動調整使下游占有率O=，這一特性可有效避免匝道上游交通量的任何變化以及其他有可能的干擾。一般取值等于或接近O，而O需通過下游流量—占有率q—o基本原理圖來設立，如圖3所示。ALINEA控制策略自被提出后，已在歐洲多個地區通過實地檢驗證明了其控制效果的可靠性，尤其是在提高車流平均速度、降低路網行程時間以及穩定交通流方面。需求—容量控制和占有率控制是在臨界狀態時才對匝道進行控制，而ALINEA對于-Ok的細微差別處理更加順暢，可以最大限度保證下游的運行容量，使交通流更加穩定，避免堵塞。

ALINEA在實際應用中還存在一些缺陷，如：經典ALINEA控制沒有考慮匝道排隊溢出問題，易使入口匝道及關聯交叉口出現排隊過長的現象;控制范圍僅為單個匝道，缺乏對多匝道協調控制的探討，難以實現系統最優。因此不少學者對其基本模型進行了優化，Zhang等對基本ALINEA模型進行了擴展，可避免匝道交通量超過其通行能力[4]。Papageorgiou和Smaragdis提出了FL-ALINEA、UP-ALINEA和X-ALINEA/Q等擴展算法[5]，可提高模型在各種場景下的性能。FL-ALINEA采用來自匝道下游檢測器的主線流量數據，當下游檢測器失效時，UP-ALINEA使用來自上游檢測器的占用率值。X-ALINEA/Q則通過限制匝道調節率，針對性解決了快速路達到最大通行能力時匝道排隊的問題。Papageorgiou提出的PI-ALINEA算法可有效緩解匝道下游的交通瓶頸[6]，Smaragdis等引入自適應控制，通過估計器獲取匝道下游實時期望占有率，提出了AD-ALINEA，該方法解決了由于天氣或交通組成而可能改變恒定期望占有率值的問題，適用于交通流狀態變化較大、臨界占有率不穩定的路段。鄭飛等探索了ALINEA算法的參數設定，通過對實際道路展開匝道動態控制并分析采集的數據，構建了匝道排隊分段約束模型，并設立控制閾值表，仿真表明該方法可平滑匝道流量脈沖，提高匝道下游車流平均速度，緩解交通擁擠[7]。

2.3? 匝道協調控制

匝道單點控制僅僅提高了單個匝道層面的運行效率，難以實現系統最優，而匝道協調控制考慮上下游若干匝道的調節，充分利用每個匝道的空間容量，改善快速路系統。這樣不僅可減輕某一處匝道的排隊壓力，還能緩解主線交通擁堵，從而彌補匝道單點控制的不足，達到系統最優。常用的匝道協調控制方法包括以下四種：

2.3.1? 系統最優協調控制（Systematic optimal control）

早在1965年，Wattleworth和Berry教授就已展開將匝道控制問題轉化為一個線性規劃問題的研究。系統最優協調控制一般以路網行程時間最小、通行流量最大等為目標函數，主線、匝道通行能力及主線限速等為約束條件，根據實時檢測的交通流狀態信息，求解交通流控制模型得到路網最優的交通狀態和匝道調節率。該方法有明確的控制模型及目標函數，理論上可以實現系統最優，但其算法求解困難，可能會出現無最優解的問題，且對交通狀態預測的要求高，因此當交通需求預測的準確度較低時，難以達到預期控制效果。同時該方法對交通異常狀態的反應很差，缺少反饋機制;一般默認通過設立約束條件使主線保持良好運行狀態，很難建立主線在擁堵或事故狀態下的交通模型。目前對于系統最優協調控制的大部分研究還處于理論探索階段，在實際應用中控制效果一般，但隨著智能技術的不斷進步，其研究前景依然非常廣闊。

2.3.2? 啟發式協調控制（Heuristic control）

啟發式協調控制不需要具體的目標函數，也不需要求實時最優解，具有一定的反饋機制，可操作性高。該方法包括合作（Cooperative）控制和競爭（Competitive）控制，合作控制中具有代表性的算法有Linked-ramp、Helper算法等，Helper算法由Lipp等提出，于1981年首次部署在科羅拉多州丹佛地區的某高速公路上，該方法將高速公路分為六組，每組包括1～7個入口匝道，并定義了六個可選匝道調節率，當某個入口匝道出現排隊時，系統將通過協調控制將該匝道的交通量有序分配至上游匝道，直至擁堵緩解結束協調控制。

競爭控制主要包括Bottleneck算法和Swarm算法等，Bottleneck算法最早是由華盛頓州交通部Jacobson等開發，首先確定每個匝道的調節率，然后當主線出現瓶頸即該處占有率超過閾值時，激活控制算法，協調控制區域內所有關聯匝道的調節率，將計算的調節率減少總量按比例分配至每個匝道，最后比較每個匝道的兩個調節率，取其中較小者作為其調節率，該方法實時性好，執行效率高，對匝道單點控制策略的魯棒性要求高。Swarm算法由Paesani等提出，該算法可分為兩層：協調控制（SWARM1）和局部控制（SWARM2），SWARM1是利用檢測器檢測實時的交通數據，然后通過線性回歸及卡爾曼濾波進行交通流預測，根據期望密度計算上游控制區域內每個匝道的調節率[8]，SWARM2中匝道調節率是根據快速路和匝道檢測到的交通流車頭時距來計算的，該算法已被應用于洛杉磯的多個洲際高速公路，控制效果較好。

2.3.3? 狀態調節器控制（State regulator control）

狀態調節器控制中最典型的算法是METALINE，屬于ALINEA的一個擴展算法[9]，其基本模型為：

rk=rk-1-Kok-ok-1-KOk-? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?（4）

式中：ok為第k個控制時段主線重要路段占有率;Ok為第k個控制時段主線下游占有率;K、K為反饋增益矩陣。

METALINE與ALINEA算法相似，其控制思路和算法求解比較簡單，并且比ALINEA更具系統性，對交通流狀態的變化更為敏感，在實際中獲得了廣泛應用。但其缺點也很明顯，如多匝道算法標定比較復雜;城市快速路入口匝道密度較大，在經常性擁堵的情況下，該算法就失去了優勢;當快速路交通狀態發生強烈變化如因事故等引起嚴重擁堵時，系統難以達到理想狀態，此時的控制效果很差。

2.3.4? 智能控制方法（Intelligent control）

由于傳統控制方法難以應對日益復雜的交通系統，因此許多學者開始利用智能控制算法，常用的有模糊控制、遺傳算法以及神經網絡等。Pappis等在進行單個交叉口控制時最先采用了模糊控制，并通過仿真證明該方法可有效降低系統車流的平均延誤。20世紀80年代，Chen提出利用模糊控制對單入口匝道進行控制，隨后Taylor等通過實驗證明該方法可有效預防高速公路交通擁擠，并且比傳統的匝道控制效果更好。陳德望結合了模糊控制和神經網絡，通過仿真證明了該智能控制方法適用于任何交通模式，并可在有效保持主線交通流處于理想密度的同時，盡可能減少入口匝道排隊[10]。喬良等采用深度Q網絡構建強化學習模型來解決無人駕駛汽車匝道匯入問題，主要從車間通信和單車控制的角度討論了單點匝道的匯入控制，缺乏對匝道區域內車輛的協調和對交通流的引導[11]。羅孝羚則是提出了一種網聯環境下的匝道車流匯入軌跡優化算法，通過仿真實驗證明所提出的模型可以使車輛總延誤減少59.7%，實現車輛以較高的速度通過匝道交通區域[12]。目前智能環境下的匝道控制研究重點在于匝道車輛的匯入控制微觀研究，缺少對快速路匝道區域內車輛的協調控制，且由于當前主流的交通仿真軟件難以實現智能環境下控制框架的構建，一般需通過二次開發實現個性化研究需求，增加了研究者的研究成本。

3? 結束語與展望

本文圍繞快速路入口匝道這一場景，介紹了目前常用的入口匝道控制算法，定時控制是最簡單的控制策略，在交通流變化較小時十分有效，但難以處理交通流狀況發生突變的情況。匝道單點控制提高了單個匝道的運行效率，但是該方法并未考慮交通流干擾，可能會影響相鄰匝道的通行效率，因而無法達到系統最優。匝道協調控制是在單點控制的基礎上，協調控制上下游若干個匝道，實現整個快速路主線的暢通。隨著車路協同和智能網聯技術的興起與發展，當前的研究熱點是將各種智能控制算法與匝道控制相結合，可有效提高匝道控制的效果和可靠性，未來可在這些方面作進一步研究。

參考文獻：

[1] 楊曉光. 考慮進出口匝道排隊約束的城市快速道路交通系統動態控制方法[J]. 長安大學學報（自然科學版），1999（2）：20-26.

[2]? Masher D P， Ross D W， Wong P J， et al. GUIDELINES FOR DESIGN AND OPERATION OF RAMP CONTROL SYSTEMS[R]. Stanford Research Institute， 1975.

[3]? Papageorgiou M， Hadj-Salem H， Blosseville J M. ALINEA： A local feedback control law for on-ramp metering[J]. Transportation Research Record Journal of the Transportation Research Board， 1991，1320：58-64.

[4]? Zhang M， Nie X， Jin W， et al. Evaluation of On-ramp Control Algorithms[D]. California： University of California， 2001.

[5]? Smaragdis E， Papageorgiou M， Kosmatopoulos E. A flow-maximizing adaptive local ramp metering strategy[J]. Transportation Research Part B Methodological， 2004，38（3）：251-270.

[6]? Wang Y， Papageorgiou M， Gaffney J， et al. Local ramp metering in the presence of random-location bottlenecks downstream of a metered on-ramp[C] // International IEEE Conference on Intelligent Transportation Systems， 2010.

[7] 鄭飛，杜豫川，孫立軍. 基于ALINEA算法快速路入口匝道單點動態控制[J]. 同濟大學學報（自然科學版），2009，37（6）：766

-771.

[8] 陸海亭，張寧，錢振東. 高速道路入口匝道控制方法及應用探索[J]. 公路，2008（8）：180-186.

[9] 康平允，干宏程，袁鵬程. 快速路入口匝道控制方法探究[J]. 物流工程與管理，2016，38（3）：201-203.

[10] 陳德望，王飛躍，陳龍. 基于模糊神經網絡的城市高速公路入口匝道控制算法[J]. 交通運輸工程學報，2003，3（2）：100-105.

[11] 喬良，鮑泓，玄祖興，等. 基于強化學習的無人駕駛匝道匯入模型[J]. 計算機工程，2018，44（7）：20-24，31.

[12] 羅孝羚，蔣陽升. 智能網聯車環境下高速匝道匯入車流軌跡優化模型[J]. 交通運輸系統工程與信息，2019，19（4）：94-100.