具有有理矩母函數跳分布的跳擴散模型下的動態基金保護定價
魏思媛,董迎輝
(蘇州科技大學 數學科學學院,江蘇 蘇州215009)
由Gerber和Shiu[1]、Gerber和Pafumi[2]提出來的動態基金保護(Dynamic fund protectio,DFP)通過保險公司注入資金的方式為投資人在經濟下行時期提供資金保護,以確保在合同期內投資人的基金價格始終高于某一預定的保護水平。近些年來,由于經濟衰退,保險公司的償付能力受到了投資人和監管機構的質疑,對這些提供保障水平的保險產品的定價問題的研究受到了廣泛的關注。
Jin等[3]和Fan等[4]研究了基金價格服從馬氏機制轉換的幾何布朗運動假設下的DFP的估值問題。劉孔潔等[5]給出了超指數跳擴散模型下動態保護基金的定價。Dong[6]在隨機利率模型下提出了一個與債券價格有關的隨機保護水平。許超和董迎輝[7]放松了文獻[5]中的常數保護水平的假設,提出了用一個跳擴散模型來刻畫障礙水平,在超指數跳擴散模型和隨機障礙下,研究了動態基金保護的定價問題。盡管超指數分布可以用來逼近許多分布,包括Gamma分布、Weibull分布和Pareto分布,然而,由于超指數分布是由指數分布密度的線性組合所決定的概率分布,其權重均不能取負值,所以Cai和Kou[8]指出,超指數分布只能用來解決一些具有絕對單調性質的分布。眾所周知,在一般的跳擴散模型下人們很難解決定價問題[9-10]。具有有理矩母函數的分布是一類比超指數分布更為廣泛的分布,它們可以用來近似任意的分布,并且在具有有理矩母函數跳分布的跳擴散模型下,仍能得到動態基金保護的定價公式。Dong和Wang[11]在具有有理矩母函數跳分布的跳擴散模型下得到了參與分紅壽險合同的定價,然而動態基金保護的產品比參與分紅壽險要復雜的多,其定價問題也更為復雜。筆者將在具有有理矩母函數跳分布的跳擴散模型和隨機障礙下研究動態基金保護的定價問題。
論文結構安排如下:第一部分介紹動態基金保護和定價模型;第二部分在具有有理矩母函數跳分布的跳擴散模型和隨機障礙下給出DPF價格的拉普拉斯變換的顯示解;第三部分對全文進行總結。
1 模型
設{Ω,ζ,{ζt}0≤t≤T,Q}為帶濾子的完備概率空間,其中{ζt}0≤t≤T為滿足通常條件的濾子,T<∞。假設所有隨機變量和隨機過程均定義在該概率空間上且關于ζT可測,Q為風險中性鞅測度。
令{N(t),t≥0}表示時間[0,t]內引起基金價格發生跳躍的事件的來到過程,假設{N(t),t≥0}是強度為λ的泊松過程。假設基金價格服從如下的跳擴散過程
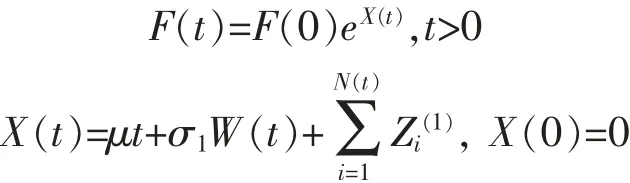
其中F(0)>0是初始基金價格,σ1>0是擴散系數,{W(t),t≥0}是一個Q測度下的標準布朗運動是獨立同分布的隨機變量序列,其密度具有有理的矩母函數
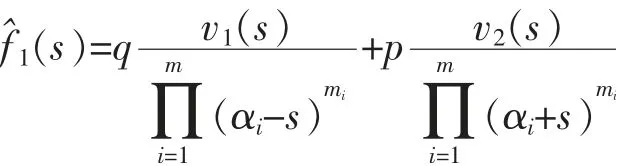
其中0<p,q<1,p+q=1,mi,m∈N+,并且是兩個至多M-1次的多項式函是無風險利率數,并且滿足
利用部分分式分解,由矩母函數f^1(s)可得到{Zi(1),i≥1}的共同密度為
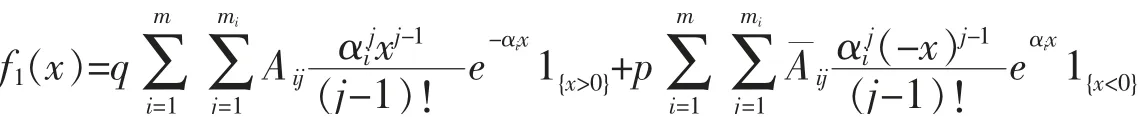
其中
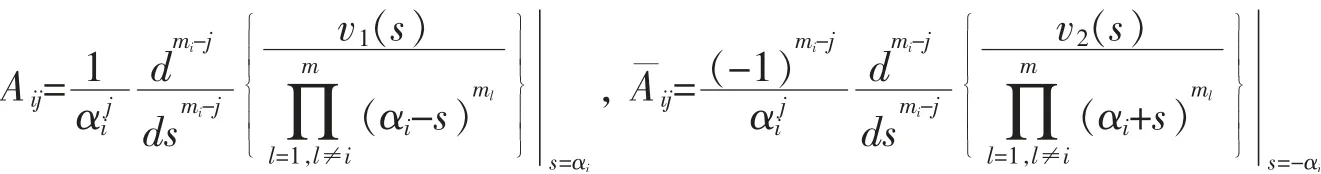
假設保護水平服從雙指數跳擴散過程
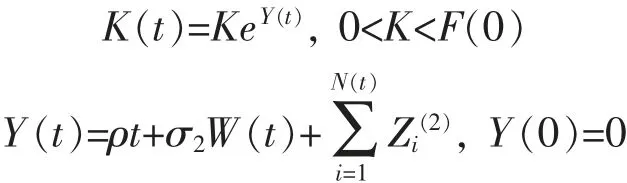
其中σ2>0為常數是獨立同分布的隨機變量序列,其密度函數為
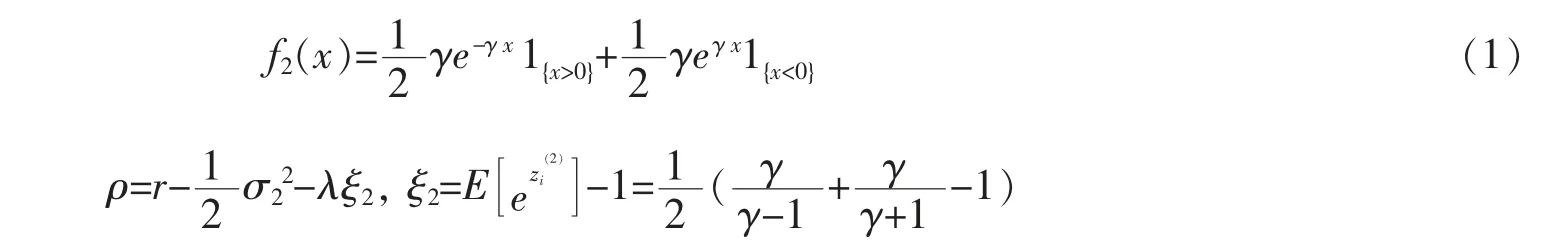
注1若假設隨機障礙也服從一個與資產價格過程相關的具有有理矩母函數跳分布的跳擴散過程,也可以用同樣的理論方法來解決動態基金保護的定價問題,然而這只會導致計算上復雜而不會帶來任何理論上的創新。因此,為簡便起見,文中僅考慮引起資產價格和障礙水平發生跳躍的事件來到過程服從相同的泊松過程,且障礙水平的跳分布服從雙指數分布。
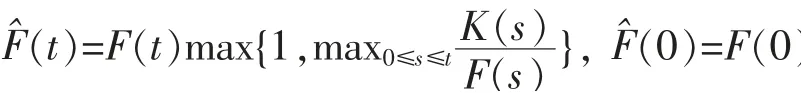
令
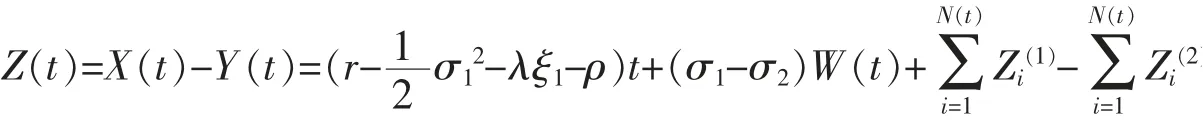
定義最小值過程為

令y<0為一給定常數,定義首中時為
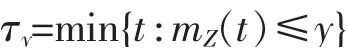
顯然,
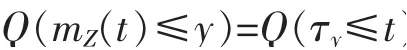
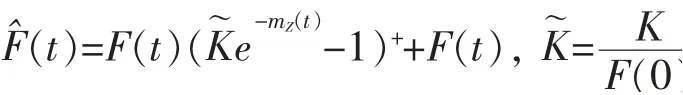
2 動態基金保護的估值
令DF(F(0),T)為具有到期日為T的動態基金保護合同所提供的動態基金保護在0時刻的價格,則根據資產定價的基本定理,有
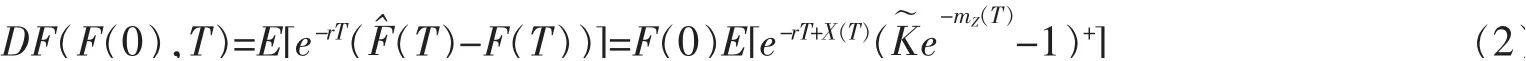
為了計算(2)式的表達式,利用Radon-Nikodym導數,定義一個新的測度Q~
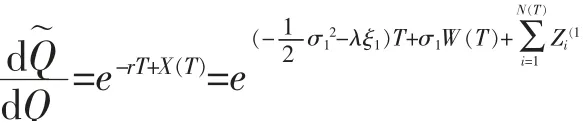
由Girsanov定理,可以得到如下結論。
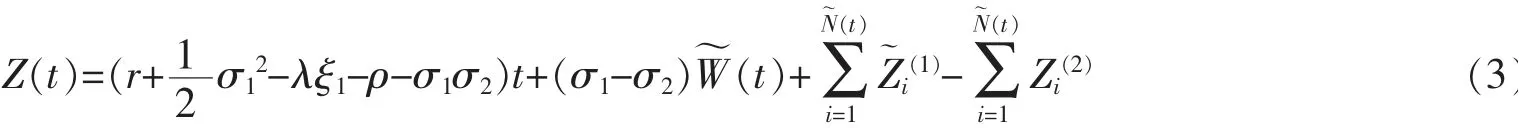
其中
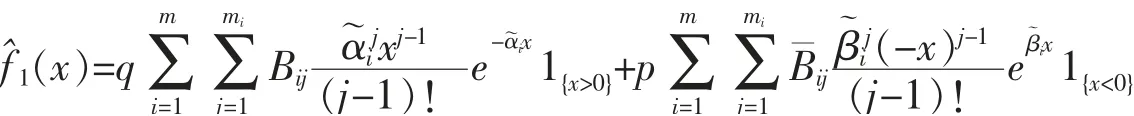
證明 利用跳擴散過程的Girsanov定理即得結論。
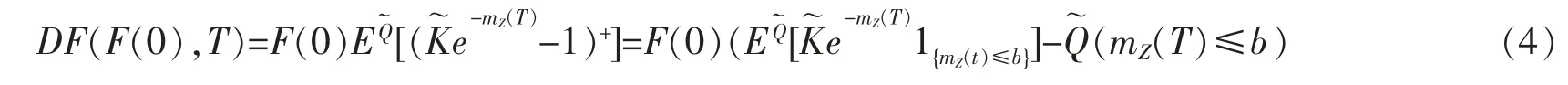
以下的結論對推導動態基金保護價格的表達公式起著非常重要的作用。
引理2令
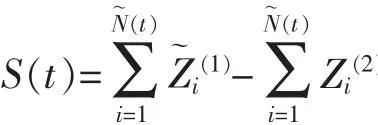
則S(t)是一個參數為λ~的復合泊松過程,其密度函數為
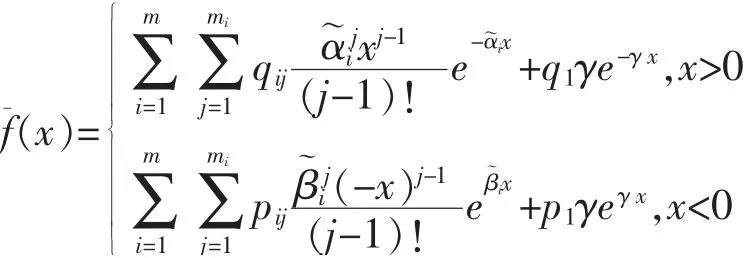
其中
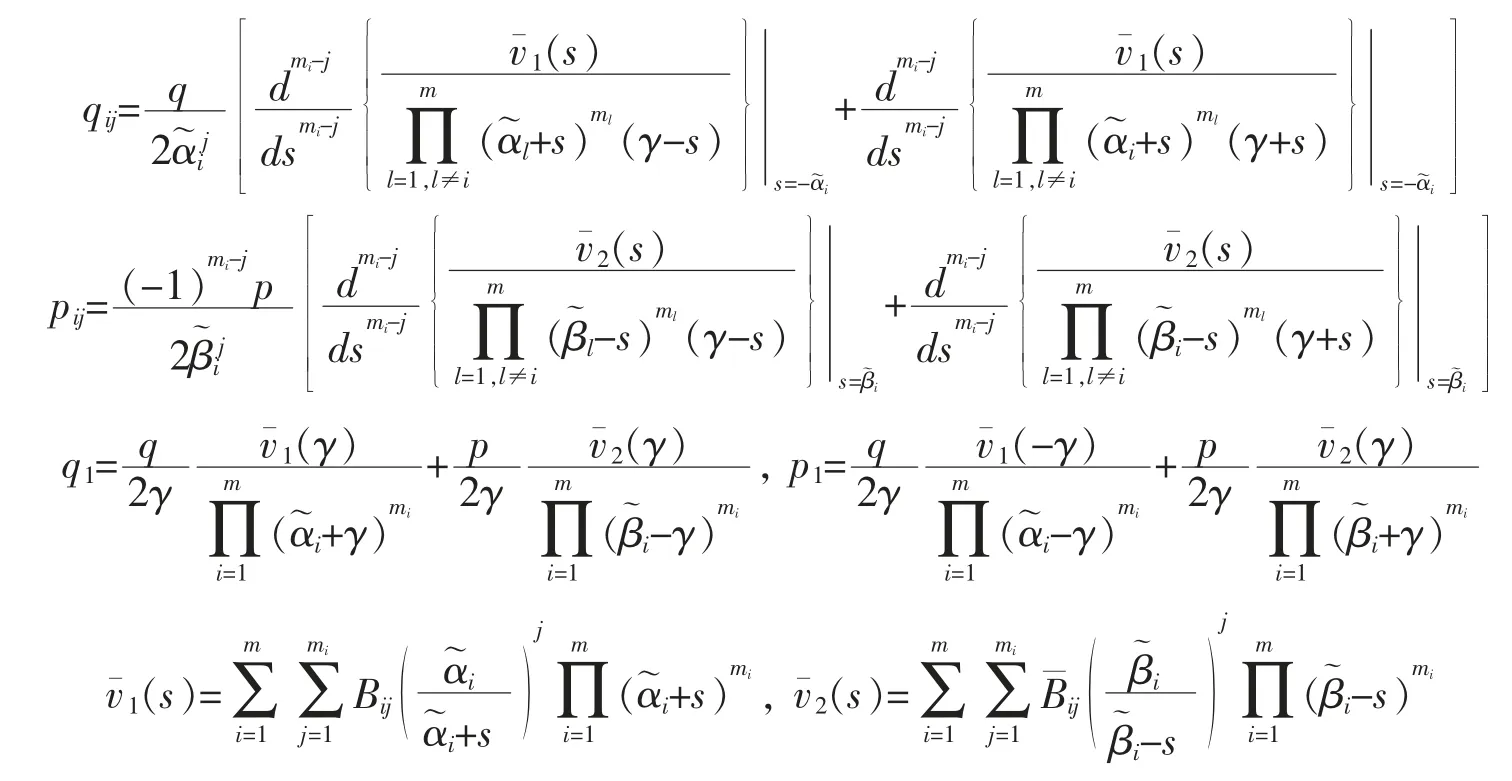
證明
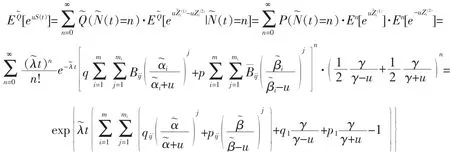
于是,由矩母函數和分布的一一對應,結論得證。
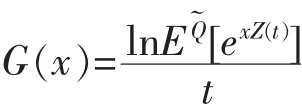
其中復數x滿足E[exZ(1)]<∞。由Levy-Khinchine公式得
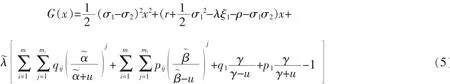
引理3令Z為公式(3)中給出的具有有理矩母函數跳分布的跳擴散過程。對任意的δ>0,y>0,τy的拉普拉斯變換為
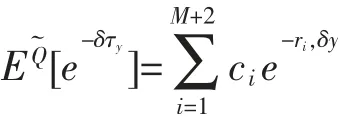
其中r1,δ>r2,δ>…>rM+2,δ是下面方程(6)的M+2互不相同的負根

系數c1,c2,…,cM+2滿足下列方程組
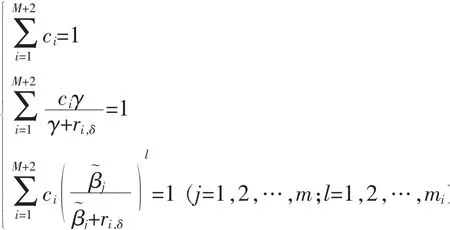
證明 參見文獻[11]中的式(3.29)。
引理4對任意的T>0,有
證明 證明過程類似文獻[7]中的引理2.6。令
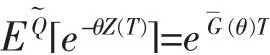
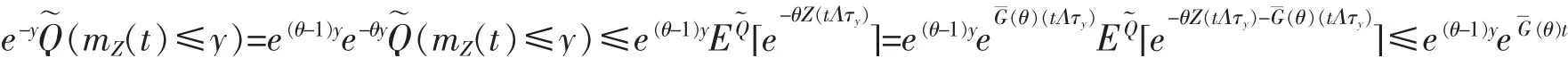
當y→-∞時,可見引理結果成立。
由引理3和引理4,可以推導出DF(F(0),T)的拉普拉斯變換。
定理1對任意的δ>0,DF(F(0),T)的拉普拉斯變換為
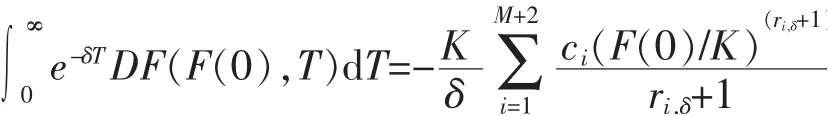
證明 由公式(4)可得

由引理4可以得到DP0(F(0),T)的拉普拉斯變換為
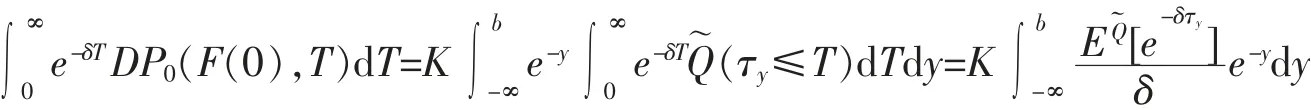
3 結語
筆者用一個具有有理矩母函數跳分布的跳擴散模型來刻畫資產價格過程,該過程能夠用來近似任意的跳擴散過程,并且在該模型下,可以得到首中時的拉普拉斯變換。進一步,筆者給出了具有有理矩母函數跳分布的跳擴散模型下動態基金保護價格的拉普拉斯變換。

