基于GIS的徐州市養老機構空間可達性研究

李保杰，紀亞洲，趙炫炫，邱文平

（江蘇師范大學 地理測繪與城鄉規劃學院，江蘇 徐州221116）

隨著我國人口老齡化的持續加劇，養老成為社會日益關注的重要問題[1]。預計到2020年，我國60歲以上老年人口將增加至2.55億人左右，占總人口比重將升至17.8%左右，老年撫養比將提高到28%左右[2-3]。近年來，我國政府雖然實施了一系列的措施來完善養老服務體系，如：推進社區養老、加強養老機構的建設等，但仍無法滿足日益增長的老齡化人口的需要。其中機構養老作為一種重要的輔助養老方式存在城區養老機構供不應求、郊區養老機構無人問津、公辦養老院嚴重不足、民辦養老院費用昂貴等一系列的問題[4-6]。因此，養老機構的空間配置布局是否科學，直接影響到政府公共服務的公平性、高效性，關系到公眾享有公共服務的質量和數量，甚至影響到“基本公共服務均等化”的目標能否實現[2]。空間可達性作為公共服務設施優化配置的重要依據而受到國內外學者的普遍關注[7-8]。

空間可達性是指從空間中任意一點到達目的地的難易程度，反映了人們到達目的地過程所克服的空間阻力大小，常用距離、時間和費用等指標來衡量。國內學者利用最短距離（時間）模型[9]、等時線模型[10]、Huff模型[11]、比例模型[12]、空間句法模型[13]、兩步移動搜索法[14]、改進潛能模型[15]等，對旅游景點[16]、醫療機構[17]、應急避難場所[18]、城市綠地[19]、基礎教育資源[20]、畜禽養殖業[21]等設施的可達性進行分析。國內外學者利用不同的可達性模型對區域公共服務設施的空間可達性進行分析，忽略了公共服務設施的服務能力等因子，其次居民點到達公共服務設施的影響因素也考慮的較少。因此，該研究以徐州市為例，在對潛能模型進行改進的基礎上對養老機構的空間可達性進行分析，以期為區域養老機構的優化布局提供技術支撐，同時為其他地區的同類研究提供借鑒。

1 研究區概況

徐州市地處江蘇省西北部，位于華北平原東南部，大部分為平原，中部和東部存在少數丘崗，屬于暖溫帶季風氣候區。截至2018年初，徐州市60周歲以上老年人口188.36萬人，占戶籍總人口的18.12%，其中80歲以上老年人口有31萬人。當地政府高度重視老齡事業的發展，加快養老機構建設步伐來應對日益嚴峻的人口老齡化問題，建成各級養老機構。該研究中養老機構的供給對象為徐州市區78所養老機構，養老需求對象為徐州市31個街道辦事處內的居民點內的老年人口。

2 數據與研究方法

2.1 數據來源與處理

徐州市養老機構數據主要來源于《徐州市主城區養老服務設施布局規劃》中的養老機構現狀分布圖（如圖1所示），以徐州市民政局、老齡網等公布的數據為參照，共采集78所養老機構數據，包括占地面積、建筑面積、床位數、護理床數和服務人員等數據；路網數據主要以徐州市2018年交通地圖為基礎，采集國道、省道、縣道、一般道路等圖層（居民出行一般不選擇高速公路和鐵路作為入院出行的方式）；人口數據主要以徐州市第六次人口普查數據為基礎，參考徐州市統計年鑒和《徐州市主城區養老服務設施布局規劃》中的相關數據；行政區劃數據采用2017年公布的行政區劃調整后的數據為基礎進行采集。利用ArcGIS10.3軟件平臺，將上述數據統一到西安80坐標系（中央經線117°），分層矢量化后保存至地理數據庫中。

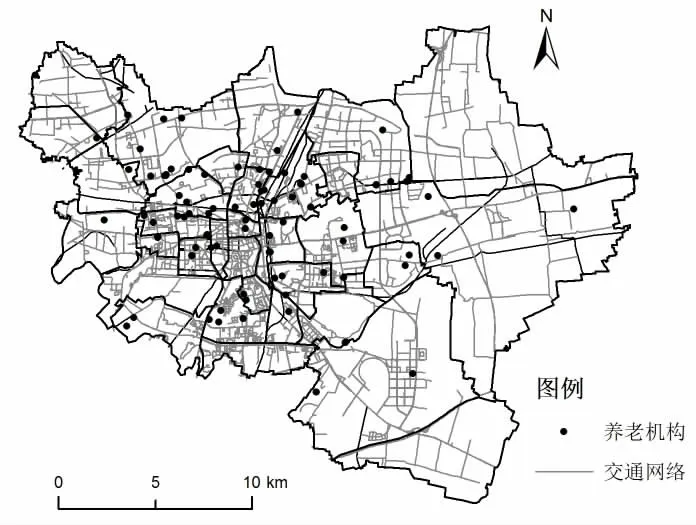
圖1 徐州市養老機構空間分布圖

2.2 研究方法

2.2.1 潛能模型

潛能模型是地理學等領域借鑒物理學中萬有引力定律用來研究社會、經濟等空間相互作用的經典模型。該模型以牛頓重力模型為基礎，但社會現象較復雜，用原始的引力模型表達現實狀況具有一定的偏差。因此，法國數學家拉格朗日在該模型的基礎上提出萬有引力潛能模型的概念。自此，該模型被廣泛用于人文地理和區域經濟等方面的研究，最終演化成為用于研究空間相互作用的潛能模型，表達式為

式中，Ai為研究區所有物體對點i產生的潛能的累加，對于養老機構而言，Ai為在考慮出行阻抗和設施的服務能力的情況下，研究區內某居民點i到養老機構的可達性，即為研究區內各養老機構對居民點i的引力值的累加；Mj為養老機構的服務能力，即表示點j的活動規模；Aij為當出行的摩擦系數為β時，物體j對i產生的潛能；Dijβ為當出行系數為β時點i到點j的出行阻抗（消耗的時間或路程）。由上式可知：出行阻抗Dijβ越小，Ai越大，則表明可達性越好。出行系數β的取值對可達性的精度產生影響，其取值與服務人群的特征和設施的服務類型相關。

2.2.2 潛能模型的改進

傳統的潛能模型僅考慮了設施的服務能力和老人入院的出行阻抗，忽略了老年人口規模等因素對入院的影響。譬如相同服務能力的兩個養老院，由于地處人口密度不同的區域，而根據傳統的潛能模型計算出養老機構的可達性是相等的，但實際情況是有區別的，主要是由于老年人口形成了對養老機構的競爭。為此，約瑟夫等在一般潛能模型的基礎上增加了人口規模因子Vj，即當Pk表示居民點k的老年人口數時，改進的潛能模型的表達式為

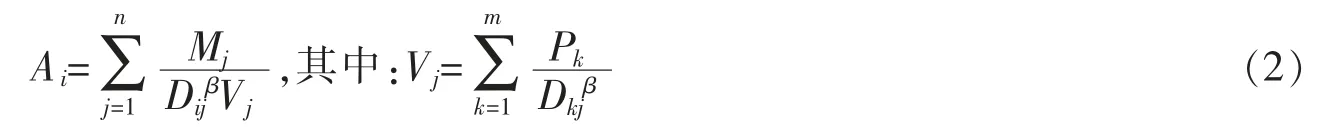
式中，Pk為居民點k的老年人口數；m為居民點的數量；Vj為引入的影響因子-老年人口規模。該模型僅從各養老機構附近的老年人口分布著手，表達了某一居民點老年人口到同一養老機構時對養老資源的競爭，以及對可達性的影響。影響養老機構服務能力包括養老機構建筑面積、床位數、護理床數、入住老人和服務人員等數據。老年人口入院時的阻抗也是影響養老機構可達性的重要因素。因此，該研究在上述模型的基礎上，參照了湯鵬飛[15]等的研究成果優化了養老機構服務能力因子（養老機構規模、硬件條件、人員結構和老人數量），構建養老機構服務能力指標體系，以此為基礎對研究區養老機構的服務能力進行測算，利用層次分析法和專家咨詢法確定各影響因子的權重。引入了基于養老機構服務能力與老年人口極限出行時間的影響因子Tij。改進后潛能模型的計算公式為

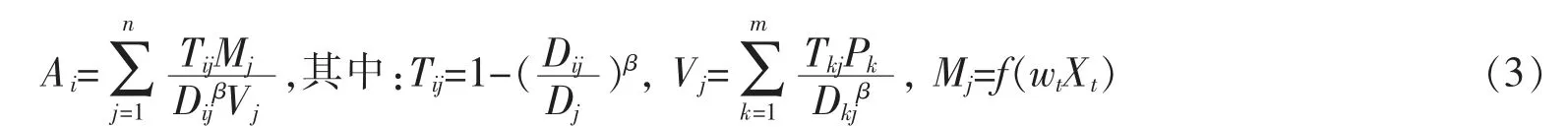
式中，Ai為居民點i的養老機構可達性；Tij為入院影響因子；Dij為居民點i到養老機構j的時間成本；Dj為該居民點j入院的極限出行時間；Mj為養老機構j的服務能力；Xt為影響該養老機構服務能力的第t個因子；Wt為第t個評價因子對應的權重；Vj為該居民點老年人口生數量；Tkj為養老機構j對居民點k的入院行為的影響；m為居民點數量，n為養老機構數量。

2.2.3 摩擦系數的選取

摩擦系數β比較理想的確定方法是以目前各養老機構的實際使用情況為基礎，結合不同距離下的居民點到該養老機構入院的人數進行回歸分析獲取。作為出行摩擦系數受到區域、時間、出行方式等綜合影響，Peeters等研究發現出行摩擦系數的取值范圍在0.9～2.2之間，為探討徐州市養老機構空間可達性分析時β的最佳取值，該研究依次將β值設定為0.9、1.0、1.1、…、2.2。對比分析不同β的取值情況下，研究區養老機構空間可達性的最大值、最小值和標準差的變化，以分析養老機構的可達性對不同的β值的敏感性程度，然后結合實地驗證，獲取最佳的摩擦系數β，研究發現當β為1.8時，各居民點的出行時間比較符合實際情況，故選取β=1.8對徐州市養老機構的空間可達性進行分析。

3 結果與分析

3.1 居民點尺度養老機構空間可達性

利用改進的潛能模型，將摩擦系數β設定為1.8，結合各養老機構的服務能力，計算各居民點的可達性，最后借助克呂金插值和指數模型對養老機構可達性進行空間插值。為了對插值結果進行驗證，利用平均絕對誤差、均方根誤差和平均相對誤差對空間插值結果進行驗證。結果表明，平均絕對誤差、均方根誤差和平均相對誤差的值均小于0.1，最后通過交叉驗證法發現精度滿足應用分析要求。得到徐州市養老機構可達性的空間分異圖（如圖2所示）。由圖可知，徐州市養老機構可達性空間分異特征如下：

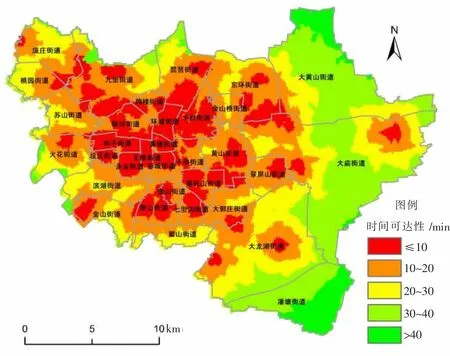
圖2 徐州市養老機構時間可達性分布圖

（1）為了直觀地表達研究區養老機構的時間可達性，該研究采用狄更斯自然斷點分類方法，將區域養老機構的時間可達性分為5個等級，最好時間可達性區域（時間可達性＜10 min）、較好時間可達性區域（10≤時間可達性＜20 min）、一般時間可達性區域（20≤時間可達性＜30 min）、較差時間可達性區域（30≤時間可達性＜40 min）、最差時間可達性區域（時間可達性≥40 min）。研究區居民點養老機構的可達性整體較好，50.02%的居民點能夠在20 min內到達相應的養老機構，其中：18.64%的居民點能夠在10 min內到達相應的養老機構；31.38%的居民點在10～20 min內到達相應的養老機構；24.17%的居民點在20～30 min內到達相應的養老機構；20.93%的居民點在30～40 min內到達相應的養老機構；到達相應的養老機構時間大于40 min的居民點的占比約4.48%。

（2）研究區養老機構時間可達性空間分異較明顯。老城區居民點養老機構時間可達性最高，分布在鼓樓區、云龍區和泉山區的交界處，上述區域為早期的建成區，人口密集，老年人口數量較多，且上述區域養老機構的服務能力較高，使得上述區域的居民點養老機構時間可達性最高；可達性較高的區域則呈環狀分布在最高可達性的外圍，如老城區的大部分區域；居民點時間可達性較差的區域主要分布在研究區東部的大廟街道、大黃山街道和潘塘街道，由于上述區域大都為經濟開發區，工礦廠房較多，居民點及其相關服務設施尚不完善，使得上述區域的時間可達性較差。

3.2 街道尺度養老機構空間可達性

以各街道內部居民點養老機構的可達性為基礎，計算各街道內養老機構可達性的平均值為各街道養老機構可達性，在ArcGIS環境下利用手動分類法，將各街道養老機構可達性分為5級（同上），得到徐州市各街道養老機構可達性分布圖（如圖3所示），由圖3可知：

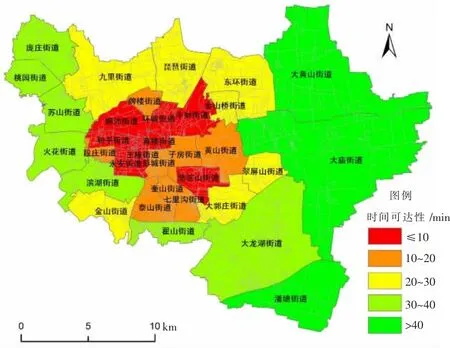
圖3 徐州市各街道可達性分級圖

（1）研究區各街道時間可達性整體較好，約69.69%街道的居民區能在30 min內到達相應的養老機構，其中：時間可達性最好的街道有8個，占比為24.24%，主要包括：和平街道、永安街道、王陵街道等；時間可達性較好的街道有8個，占比為24.24%，主要包括：段莊街道、牌樓街道、彭城街道等；時間可達性一般的街道有7個，占比為21.21%；時間可達性較差的街道有10個，占比為30.01%；時間可達性最差的街道有3個，占比為9.09%，包括大黃山街道、大廟街道、潘塘街道。

（2）從各街道養老機構可達性的空間分布來看，各街道養老機構可達性存在明顯的圈層結構。研究區可達性最好的區域主要集中在老城區和平街道、永安街道和王陵街道等且呈片狀區域集中分布；時間可達性較好的區域主要分布在最好時間可達性區域東南部的外圍，如：彭城街道、子房街道和黃山街道等；時間可達性一般的區域主要分布在西北與東南軸線的北部，如九里街道、琵琶街道和東環街道等；可達性較差的區域主要分布在西北與東南軸線的南部，如：龐莊街道、桃園街道、蘇山街道等；時間可達性最差的區域主要分布在研究區東部，如大黃山街道、大廟街道、潘塘街道，上述街道大都為近年來開發的區域，相關的養老設施尚不完備，同時受到區域邊際效應的影響，從而導致上述區域養老機構可達性較差。

4 結語

養老機構的空間分布格局是由居民點空間分布、交通網絡、老年人的分布和政策等因素綜合作用的結果，而養老機構的床位數、規模和區位等因素是導致區域養老機構配置不合理的重要因素。因此，該研究在傳統潛能模型的基礎上，引入養老機構服務能力和老年人極限出行時間等因子對其進行改進，借助該模型對研究區養老機構的可達性從居民點尺度、街道尺度進行分析。形成如下結論：

（1）在傳統潛能模型的基礎上，對養老機構的服務能力進行優化，結合老年人口極限出行時間對該模型進行改進；在分析不同的摩擦系數對養老機構可達性影響的基礎上，獲得最佳的摩擦系數1.8；通過對各居民點可達性數據進行半變異函數計算，確定了空間可達性空間插值的最優模型為指數模型。最后借對插值結果進行驗證，結果表明插值精度滿足應用分析要求。

（2）研究區養老機構的可達性整體較好，其中50.02%的居民點能夠在20 min內到達相應的養老機構；24.17%的居民點在20～30 min內到達相應的養老機構；25.41%的居民點到達相應的養老機構時間大于30 min。老城區養老機構空間可達性最高，隨著與老城區的距離逐漸增大，可達性較高的區域則呈環狀分布在高可達性區域的外圍；可達性最差的區域主要集中在研究外圍。

（3）該研究在進行養老機構的空間可達性研究時，僅考慮了養老機構區位、規模和等級、交通網絡的分布、居民點的位置和老年人口的分布等因素，忽略了老年人口的入院意愿、經濟能力等主觀因素；其次，該研究僅選擇徐州市養老機構的可達性進行分析，沒有將徐州的養老機構可達性水平與其他城市進行比較，無法確定其整體水平，這將是筆者今后進一步研究的方向。