基于三角模糊數截集的基坑支護結構穩定性分析

廖 瑛，孫 李

（蘇州科技大學 土木工程學院，江蘇 蘇州215011）

基坑工程是一項風險大、難度高的基礎性工程。為了保證基坑工程的穩定性并將周圍土體的變形控制在一定范圍內，必須對基坑的坑壁進行相應的支護和加固，因此，對基坑支護結構的穩定性研究是一項重要的巖土工程課題。

目前，基坑支護結構穩定性的設計中，主要采用定值的安全系數法，將抗力效應與荷載效應的比值，即安全系數作為衡量結構安全程度的標準[1]。由于這種方法將土體力學參數作為確定性參數處理，忽略了粘聚力、內摩擦角及重度等參數的隨機性與模糊性特點，故而雖然計算簡便但缺陷也不可避免。筆者擬首先根據α截集法[2]的三角模糊數模型將土體力學參數離散為區間數，再根據結構可靠度理論[3]建立懸臂式基坑支護結構可能的失穩模式的極限狀態方程，最后采用JC法[4]計算結構的可靠指標，以定量地度量結構的可靠性。

1 基坑支護結構穩定可靠性分析的功能函數

1.1 抗傾覆穩定可靠性分析功能函數

根據結構可靠度理論，懸臂式基坑支護結構的抗傾覆穩定性驗算計算簡圖如圖1所示，其功能函數可表示為

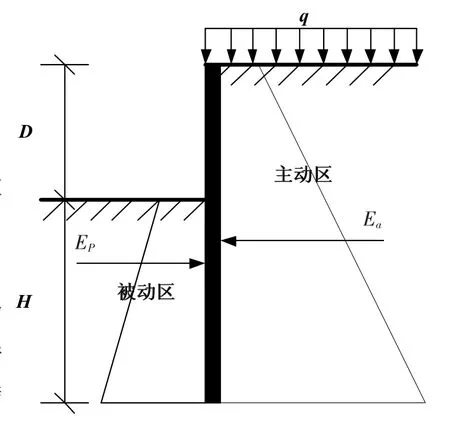
圖1 土壓力分布圖

式中，MR是抗傾覆力矩（kN·m）；MS是傾覆力矩（kN·m）。前者為墻前的被動土壓力Ep對轉動點的轉動力矩，后者為墻后的主動土壓力Ea對轉動點的轉動力矩。對于不同的支護結構，轉動點也有所不同。例如：懸臂式基坑支護結構，轉動點位于墻角處；單（多）點支撐，轉動點位于底部支撐處；重力式基坑支護結構和土釘墻結構，墻體自重對轉動點產生的抗傾覆力矩還應該被考慮在內[5]。

1.2 抗滑移穩定可靠性分析功能函數

按照結構可靠度理論，懸臂式基坑支護結構抗滑移穩定性分析計算簡圖亦如圖1所示，其功能函數可表示為

式中，Ep為被動土壓力（kN）；Ea為主動土壓力（kN）。

1.3 抗整體失穩可靠性分析功能函數

基坑整體穩定性分析實際上是對帶支護結構的垂直土坡的分析。采用簡化的瑞典條分法進行穩定可靠性分析，懸臂式基坑支護結構的抗整體失穩計算簡圖如圖2所示，其功能函數可表示為

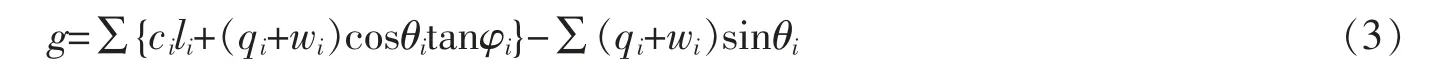
圖中及式中，ci為第i土條滑弧面處土的粘聚力（kPa）；φi為第i土條滑弧面處土的內摩擦角（°）；bi為第i土條的寬度（m）；li為第i土條的滑弧長度；θi為第i土條滑弧面中點處法線與豎直方向的夾角（°）；wi為第i土條的自重（kN）；qi為第i土條上的超載（kPa）。

整體穩定性計算中，重要的是如何找到最危險滑弧面。根據大量工程的實驗和研究，可以采用“三點定圓”的方法對最危險滑弧面進行搜索[6]。以樁頂為原點建立笛卡爾坐標系并將其劃分為①、②、③、④4個區域，則最危險滑弧通過樁底端，并且其對應的圓心在②區域（如圖2所示）。如此即可對該區域利用MATLAB編程計算進行全域搜索，尋找最危險的滑弧面和圓心。

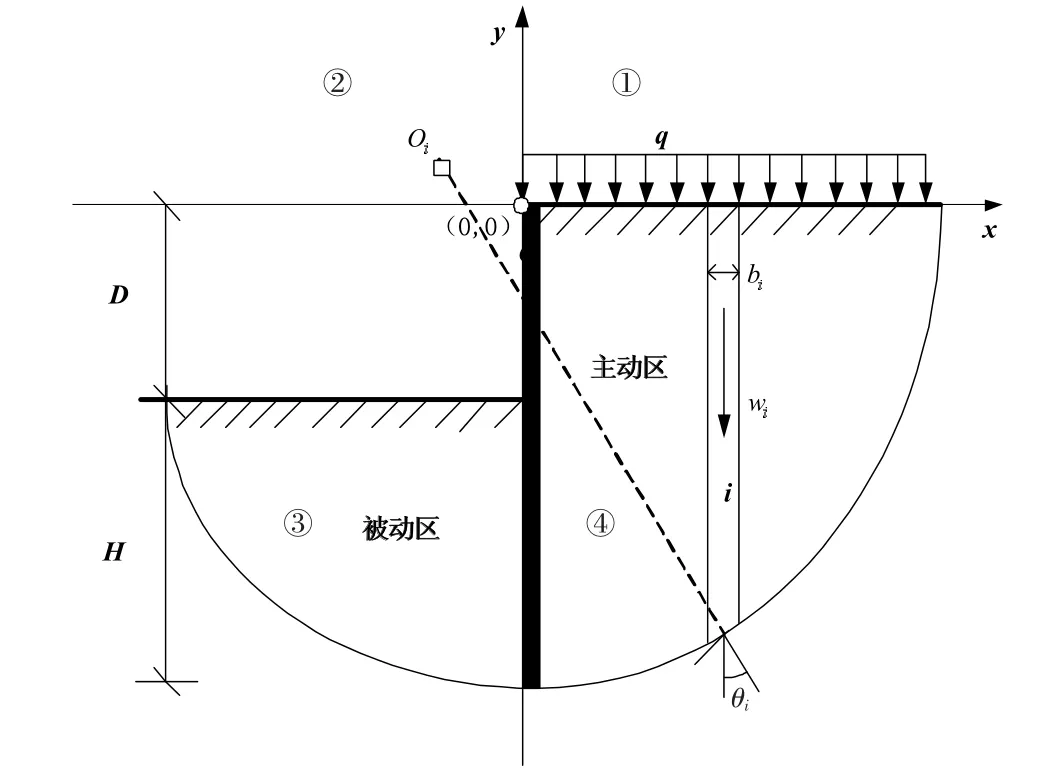
圖2 抗整體失穩危險滑弧面的搜索

2 基于α截集法的土體模糊參數

2.1 三角模糊數的確定[7]

巖土力學參數如抗剪強度參數c與φ、抗壓強度σc和抗拉強度σt等參數都具有模糊性和隨機性特點，其不確定性特點會對計算結果產生極大的影響。在此采用三角模糊數來表示參數的可能性分布。定義若為一個三角模糊數，如圖3所示，其隸屬函數可表示為

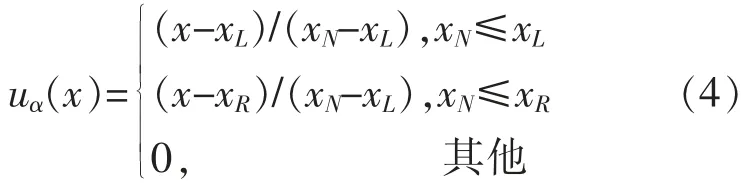
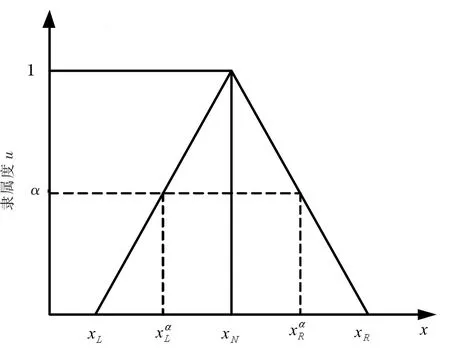
圖3 三角模糊數的隸屬函數

依據三角模糊數的定義，統計分析地下巖土力學參數的實測數據，可以把該三角模糊數的上限定義為xR，下限定義為xL，中值則為xN，當三角模糊數為對稱時中值即為參數的均值。對于基坑支護結構的穩定性問題，隸屬度表示的是模糊區間對于“穩定”這一模糊概念的隸屬程度（0≤u≤1），比如u=1表明模糊區間退化為確定的一點，即不考慮問題的模糊性；而u=0則表明界定穩定的模糊區間最大。

2.2 三角模糊數的截集水平

為能充分體現工程統計數據對計算結果的影響狀況以及不同截集水平下結構的可靠性，根據模糊數截集水平定義[8]，設A∈F（U），α∈[0，1]，記

2.3 土體模糊參數的確定

設基坑支護結構土體模糊參數的均值符合對稱三角形模糊數[xL，xN，xR]模型，如圖3所示，取某一個α截集水平（0≤α≤1），將其離散得到區間數為圖3 中，xN為模糊參數的均值，分別為α截集上的模糊數的左右兩端值，α=0時的即為xL，xR。對于對稱三角模糊數[9]，在α截集上有如下關系式成立

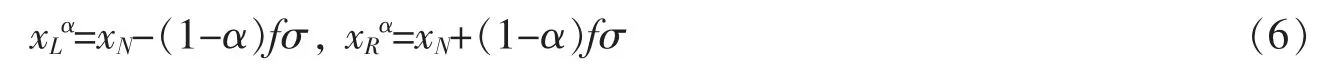
式中，σ為參數的標準差，反映參數隨機性特點。f為模糊程度系數，其取值大小反映參數的模糊性特點，根據相關專家的經驗和結論，常取值f∈[0.5，1.5]。

3 可靠指標的計算方法

可以采用JC法計算懸臂式基坑支護結構三種失穩模式的可靠指標，其具體計算流程為：

（1）建立基坑支護結構穩定可靠分析的功能函數g（x1，x2，…，xn），對全部的變量xi，選取設計驗算點的初值xi*，一般取xi*為變量xi的均值μxi，并對非正態變量進行當量正態化轉化。

（2）計算各隨機變量的靈敏度系數αi

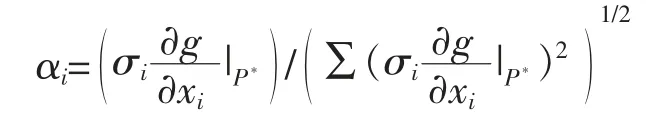
（3）利用公式計算可靠指標β

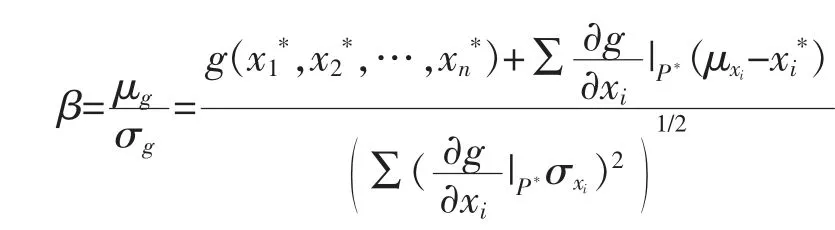
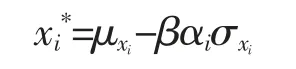
（5）重復（2）~（4）的計算步驟，直至前后兩次計算的β差值在容許誤差范圍內，且滿足g（x1，x2，…，xn）=0，則迭代計算過程終止，最后一次算得的β即為支護結構的穩定可靠指標。

4 實例及結論

某擬建基坑工程項目，地處新開發區。基于地面周邊環境狀況，換算成地面均布超載為q=15 kPa。基坑的支護結構采用懸臂式排樁支護，基坑開挖深度6.5 m、嵌固深度8.5 m，樁身穿越土層情況如圖4所示，相關土層參數實測見表1。

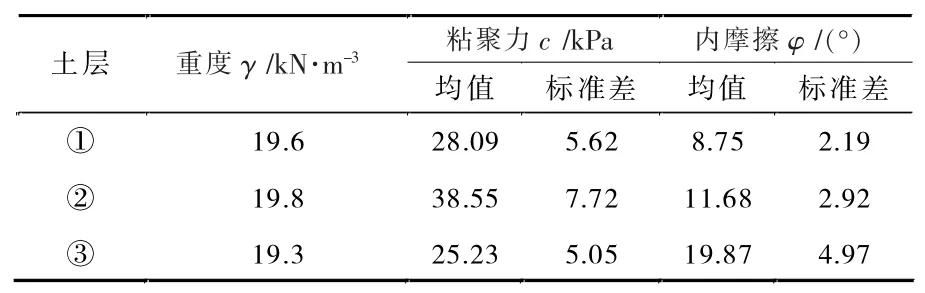
表1 相關土層參數實測表

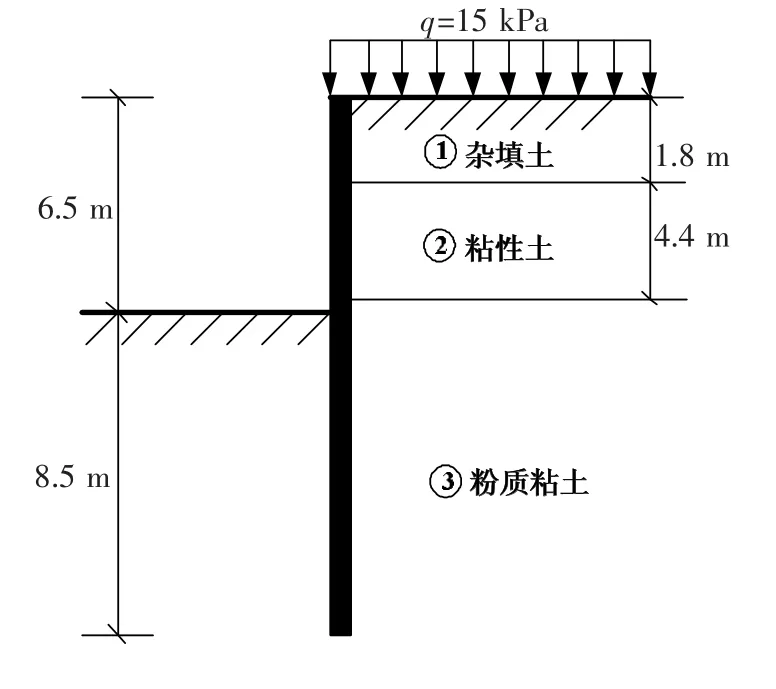
圖4 樁身穿越土層示意圖

為計算簡便，文中分別對主動區和被動區土層參數按土層厚度進行加權平均處理，且僅將摩擦角和粘聚力作為隨機變量處理，相關隨機變量的計算參數見表2。

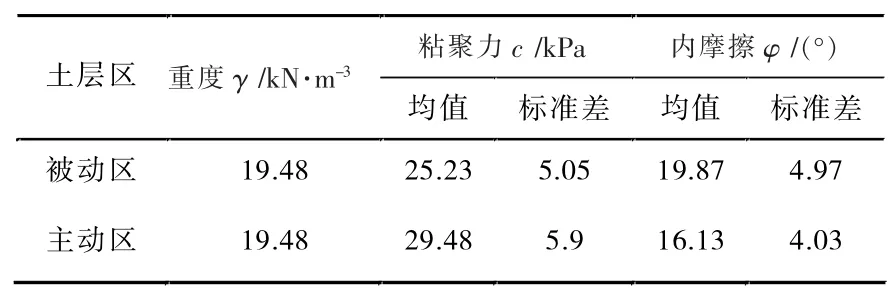
表2 按土層厚度加權平均處理的隨機變量計算參數

根據以上計算參數，采用MATLAB編程對該懸臂式基坑工程實例進行抗傾覆、抗滑移和抗整體失穩的穩定可靠度分析，得出相關計算結果如圖5和圖6所示。

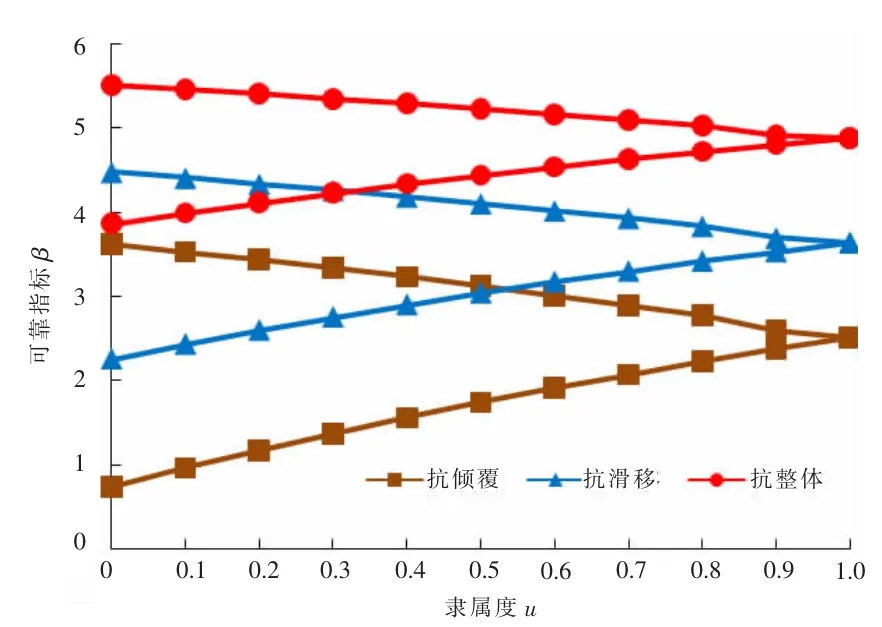
圖5 隸屬度u-可靠指標β關系曲線（取f=1）

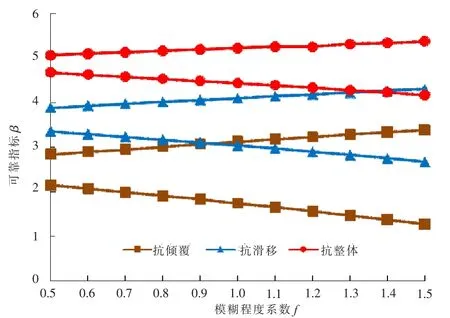
圖6 模糊程度系數f-可靠指標β關系曲線（取u=0.5）

由圖5知，當模糊程度系數取為中值f=1（0.5≤f≤1.5）時，懸臂式基坑支護結構三種穩定性分析模式的模糊隨機可靠指標都不是一個定值，而是分布在一定的三角形區域內，這是因為表示土體物理力學指標的模糊隨機變量在α截集上也表現為三角形分布；并且隨著隸屬度的增大，可靠指標分布的閉區間跨度逐漸減小。當隸屬度等于0時，傾覆穩定可靠指標閉區間跨度最大，滑移穩定可靠指標閉區間跨度居中，整體穩定可靠指標閉區間跨度最小。當隸屬度等于1時，模糊隨機可靠度問題轉化為隨機可靠度問題，閉區間的中點即為隨機可靠指標。此時傾覆可靠指標最小為2.511，相應的失效概率為0.79%；滑移可靠指標居中為3.632，相應的失效概率為0.014 011%；整體穩定性可靠指標最大為4.878，相應的失效概率為0.000 053 508%。由于基坑支護結構是臨時性工程，故可以0.1%～1%作為基坑支護結構失穩的概率標準[10]，以上隸屬度等于1的計算結果表明該基坑支護結構三種可能的失穩模式的失效概率均未超過失穩概率標準的上限1%，故該基坑不會發生失穩破壞。此外，鑒于此時的抗傾覆可靠指標最小，所以可以判定傾覆失穩模式是該基坑支護工程的控制性失穩模式，有必要對其做進一步的研究。

由圖6可知，當取隸屬度為中值u=0.5（0≤u≤1）時，三種基坑失穩模式的模糊隨機可靠指標分布的閉區間跨度都隨模糊程度系數的增大而增大，這是因為模糊程度系數的增大會導致問題模糊性因素的影響加大，從而使得模糊可靠指標上下限之間的區間變大。當取f為區間[0.5，1.5]上的某一定值時，傾覆穩定可靠指標分布的閉區間跨度均最大，滑移穩定可靠指標分布的閉區間跨度均居中，而整體穩定可靠指標分布的閉區間跨度均最小。這說明模糊程度系數對該基坑工程實例中傾覆失穩模式的影響最大。結合圖5的結論，即傾覆失穩模式是該懸臂式基坑支護結構的控制性失穩模式，接下來針對該失穩模式做進一步的分析。

以下分析中對該基坑支護結構的傾覆失穩模式，分析了f=0.5、1.0、1.5時隸屬度u-可靠指標β的關系曲線，如圖7所示。

由圖7可知，模糊程度系數可以極大地影響該基坑工程抗傾覆可靠指標β的閉區間跨度，以隸屬度u=0為例，當f=0.5時，β的取值區間為[1.739，3.121]；當f=1.0時，β的取值區間增大為[0.736，3.615]；當f=1.5時，β的取值區間進一步增大為[0.100，4.023]。隨著隸屬度的增大，三個模糊程度系數對應的可靠指標取值區間均逐漸減小，直至隸屬度u增大為1時，三者對應的可靠指標合三為一，此時的可靠指標均等于2.511，說明模糊隨機可靠度問題已經退化為隨機可靠度問題。

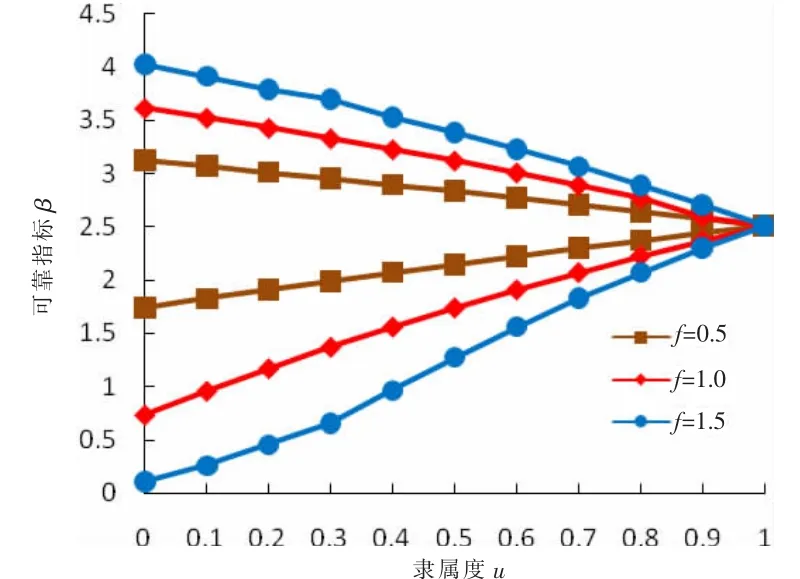
圖7 傾覆失穩模式中不同模糊程度系數下隸屬度u-可靠指標β關系曲線

根據隨機變量均值、標準差、變異系數三者之間的關系，由表2可計算得到主動區、被動區粘聚力的變異系數δc均為0.2、內摩擦角的變異系數δφ均為0.25。為研究參數變異性對傾覆可靠指標的影響，以下將變異系數取為原值，即δc=0.2、δφ=0.25的0.5、1、1.5倍，計算了隸屬度u-可靠指標β的關系曲線，如圖8所示。

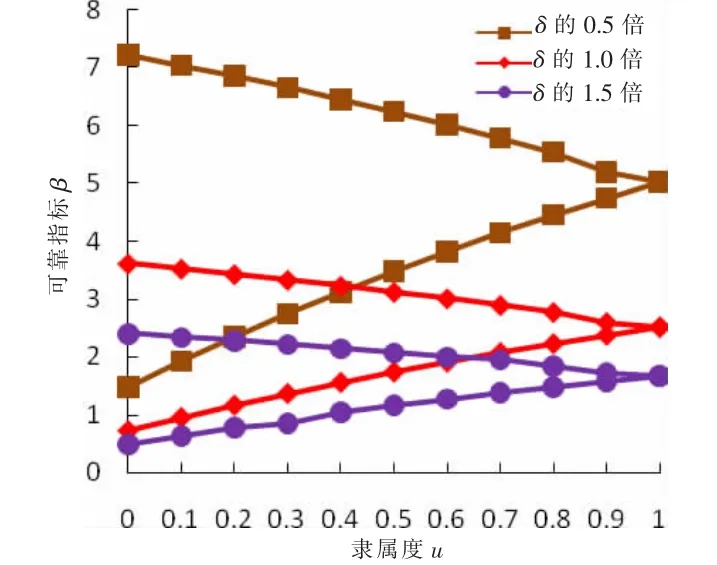
圖8 傾覆失穩模式中不同變異系數下隸屬度u-可靠指標β關系曲線（取f=1）

由圖8知，變異系數可以極大地影響基坑工程抗傾覆可靠指標β的閉區間跨度，這種影響在隸屬度u=0時體現得尤為明顯，此時當變異系數取為原值即δc=0.2、δφ=0.25時，β的取值區間為[0.736，3.615]；當變異系數取為原值的0.5倍時，β的取值區間迅速增大為[1.471，7.231]；當變異系數取為原值的1.5倍時，β的取值區間減小為[0.490，2.410]。隨著隸屬度的增大，三組變異系數對應的可靠指標取值區間均逐漸減小，直至隸屬度u增大為1，即模糊隨機問題退化為隨機問題時，隨著隨機變量變異系數由原值的0.5倍增大到1倍直至增大到1.5倍，抗傾覆可靠指標由5.022迅速減小到2.511，再進一步減小為1.674。這說明隨機變量的變異系數對于隨機可靠度問題的計算至關重要，有必要通過大量的實測數據來統計確定隨機變量的變異系數。

5 結語

基于α截集以及結構可靠度相關理論，將模糊隨機可靠度問題轉化為隨機可靠度問題，并構建功能函數，利用MATLAB軟件編制程序計算了一個懸臂式基坑支護結構的可靠指標，通過對計算結果的分析得到了如下結論：

（1）土體力學參數采用三角模糊數計算模型，相應得到的抗傾覆、抗滑移、抗整體失穩可靠指標均隨隸屬度的變化分布在一定的三角形區域內。

（2）在不考慮地下水等因素的影響下，參數模糊性和隨機性對計算結果的影響為：隨著參數隸屬度的增大，可靠指標分布的閉區間跨度減小；隨著模糊程度系數的增大，可靠指標分布的閉區間跨度增大；參數變異系數的增大會導致可靠度指標迅速減小。

（3）計算與分析成果是基于一個懸臂式基坑工程實例得到的，鑒于巖土工程問題的復雜性，巖土力學參數的變異性與模糊性等不確定性特點不具有可復制性，故相關規律性的探討還有待進一步的理論研究與實踐檢驗。