基于繼發性免疫失敗的麻疹模型及其動力學行為

王 晗, 李輝來, 李文軒

(吉林大學 數學學院, 長春 130012)

麻疹病毒傳染性極強, 是一種常見的帶有潛伏期的呼吸道疾病[1], 而且并非所有接種麻疹疫苗的個體均可獲得特異性免疫力[2]. 個體接種麻疹疫苗后未能發生血清轉化的情況稱為原發性免疫失敗[3-4], 繼發性免疫失敗是指個體接種麻疹疫苗后產生特異性抗體, 但抗體水平含量會隨接種時間的增加而降低, 從而失去保護作用[5-8], 原發性免疫失敗和繼發性免疫失敗都屬于疫苗免疫失敗現象. 目前, 已有研究表明存在繼發性免疫失敗的案例[9-17], 在繼發性免疫失敗后感染麻疹病毒的患者具有一定的傳染性, 并表現出較輕的臨床癥狀[18]. 基于此, 本文建立一類基于接種疫苗引發的繼發性免疫失敗的麻疹模型, 并分析該模型的動力學行為. 本文討論的模型可用于刻畫麻疹病毒在不同免疫狀態群體中的傳播過程, 考察接種疫苗后產生特異性抗體但抗體水平低于保護閾值的群體對病毒傳播的影響, 并給出合理的抗疫措施, 對麻疹疫情防控有一定的作用.

1 模型構建

假設每個個體均可通過接種麻疹疫苗獲得免疫力, 即接種疫苗一定會發生免疫反應： 個體可能發生疫苗免疫失敗, 也可能獲得永久免疫力. 在該假設條件下, 將總人口分為6個倉室, 其中M(t)表示在t時刻未達到初免年齡的嬰兒數量,S(t)表示在t時刻達到初免年齡且未接種過疫苗的易感者數量,V(t)表示在t時刻達到初免年齡且可能發生疫苗免疫失敗的個體數量, 倉室V中個體體內平均抗體水平高于倉室S中個體體內平均抗體水平含量,E(t)表示在t時刻處于潛伏期的患者人數,I(t)表示在t時刻具有傳染性的患者人數,R(t)表示在t時刻移出的人數(包括因接種疫苗獲得永久免疫力的人群, 因患病獲得永久免疫力的人群, 患病后隔離的人群等).因此在t時刻, 總人口數量為

N(t)=M(t)+S(t)+V(t)+E(t)+I(t)+R(t).

本文假設Λ表示倉室M的常數輸入率, 隨著年齡增長, 倉室M中個體達到初免年齡的比例為θ1, 其中達到初免年齡個體不接種疫苗的比例為a1, 達到初免年齡個體接種疫苗并發生繼發性免疫失敗的比例為a2, 疫苗接種者獲得永久免疫力的比例為1-a1-a2; 倉室V中個體通過再次接種疫苗進入倉室R中的比例為θ2;β1,β2,β3分別為倉室M,S,V中的個體與具有傳染性的感染者I的傳染系數; 倉室E中的感染者從潛伏期進入傳染期的轉移率為σ; 倉室I中具有傳染性的感染者移出率為γ;ξ1,ξ2,ξ3,ξ4,ξ5,ξ6分別表示各倉室的死亡率, 易知ξi(i=1,2,…,6)是正常數.

基于傳染病的傳播過程和上述假設條件, 本文構建如下常微分方程系統:

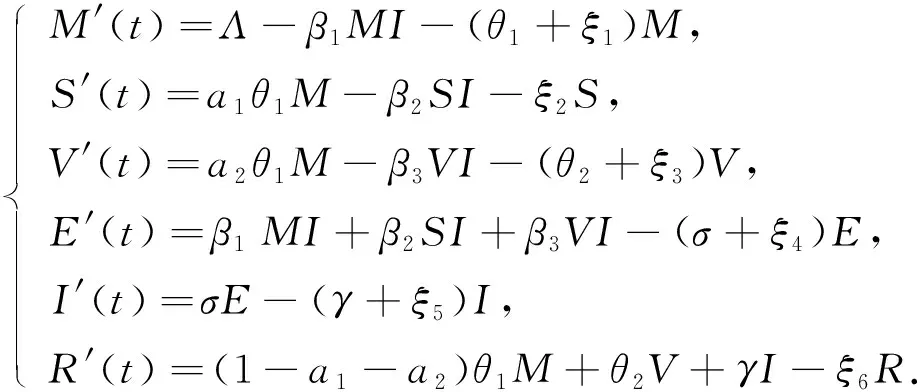
(1)

模型(1)的麻疹病毒傳播過程如圖1所示.

圖1 模型(1)的麻疹病毒傳播過程Fig.1 Transmission process of measles virus in model (1)

由圖1和系統(1)可知, 移出人群R未參與麻疹病毒的傳播過程, 所以可考慮如下常微分方程組:

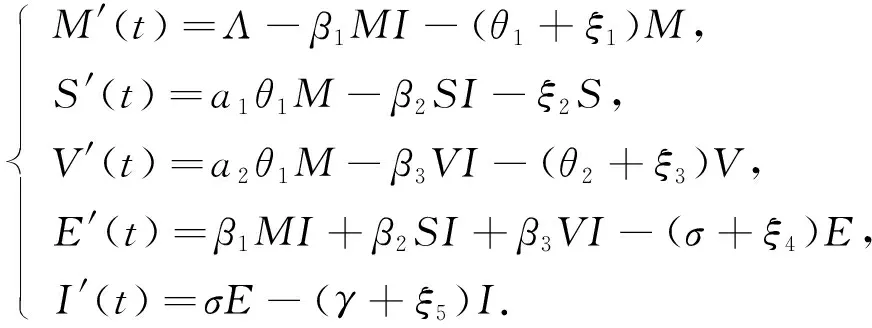
(2)

由M′≤Λ-(θ1+ξ1)M, 易得

假設ξ*=min{ξ1,ξ2,ξ3,ξ4,ξ5}, 將系統(2)各方程相加可得

經簡單計算得

因此, 系統(2)的ω極限集為如下有界區域:

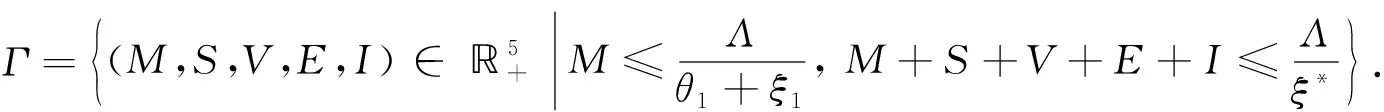
(3)

易知, 集合Γ關于系統(2)是正不變的.

2 平衡點

系統(2)在可行域Γ中有無病平衡點P0=(M0,S0,V0,0,0), 且P0滿足如下方程組:

本次調查發現，在影響求職的因素中，81%的學生認為實踐經驗最重要，56%的認為家庭社會關系最重要，其他分別為較好的心理素質、各級各項獲獎、等級證書，學習成績由第一位下降為第六位。建議學校對畢業生進行求職培訓，讓學生了解用人單位的選聘要求，學會成功推銷自己。

因此可得無病平衡點為

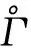
(4)

從而可得傳染病平衡點為

3 基本再生數

基本再生數R0是在傳染病建模中最重要的參數, 其描述一個具傳染性的患者在平均感染期內將病毒傳染給易感者的平均人數.如果R0<1, 則傳染病會滅亡; 如果R0>1, 則傳染病仍會發生.

根據文獻[19]可得

系統(2)的基本再生數R0定義為下一代矩陣FU-1的譜半徑, 記為R0=ρ(FU-1), 其中ρ(M)表示矩陣M的譜半徑.經簡單計算可得

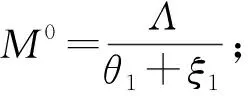
4 全局穩定性

下面證明R0是系統(2)的一個閾值參數: 當R0≤1 時, 無病平衡點P0是全局漸近穩定的, 麻疹疫情最終會消亡; 當R0>1時, 無病平衡點P0是不穩定的, 傳染病平衡點P*是全局漸近穩定的, 且麻疹會持續存在.

4.1 無病平衡點的全局穩定性

定理11) 如果R0≤1, 則無病平衡點P0是系統(2)中唯一的平衡點, 并在Γ中全局漸近穩定;

證明： 1) 考慮如下Lyapunov函數:

L(E,I)=σE+(σ+d)I,

則L沿系統(2)解軌線的全導數為

4.2 傳染病平衡點的全局穩定性

證明： 考慮如下Lyapunov函數:

因為

φ(r)=r-r*-r*lnr+r*lnr*≥0,

當且僅當r=r*時,φ(r)=0, 所以Q(M,S,V,E,I)是正定的, 于是Q沿方程(2)解軌線的全導數為

將式(6)代入式(4), 整理可得

已知函數Φ(s)=1-s+lns在定義域上為非負函數, 則當且僅當M=M*,S=S*,V=V*,E=E*,I=I*時,因此集合中唯一的緊不變子集是單點集{P*}.根據LaSalle不變性原理[16]知, 當R0>1時,P*在中是全局漸近穩定的.證畢.

綜上所述, 可得如下結論： 當基本再生數R0≤1時, 無病平衡點是全局漸近穩定的, 即疾病將會消亡, 表明疫苗接種可有效控制傳染病的傳播, 進而徹底消滅疾病； 當基本再生數R0>1時, 傳染病平衡點是全局漸近穩定的， 表明個體抗體水平會隨著接種疫苗時間的增加而下降， 發生繼發性免疫失敗現象， 這種情況可導致傳染病持續地流行.