單位球上含梯度項(xiàng)的橢圓邊值問(wèn)題徑向解的存在性與唯一性
唐 穎, 李永祥
(西北師范大學(xué) 數(shù)學(xué)與統(tǒng)計(jì)學(xué)院, 蘭州 730070)
0 引 言
非線性項(xiàng)中含梯度項(xiàng)的一般橢圓邊值問(wèn)題描述了等離子體物理學(xué)、 氣體動(dòng)力學(xué)及固體物理學(xué)中的許多現(xiàn)象, 研究其解的存在性與唯一性有一定的理論意義. 本文討論單位球上含梯度項(xiàng)的橢圓邊值問(wèn)題(BVP):

(1)
徑向解的存在性與唯一性, 其中:Ω={x∈N: |x|<1},+=[0,+∞),N≥2;f:I××+→為非線性連續(xù)函數(shù),I=[0,1].
對(duì)非線性項(xiàng)中不含梯度項(xiàng)的特殊情形, 即簡(jiǎn)單橢圓邊值問(wèn)題:
其徑向解的存在性已有較深入的研究[1-4].對(duì)非線性項(xiàng)含梯度項(xiàng)的情形, 當(dāng)Ω為環(huán)形區(qū)域或球外部區(qū)域時(shí), 文獻(xiàn)[5-7]討論了其正徑向解的存在性, 其中文獻(xiàn)[5-6]在非線性函數(shù)f(r,ξ,η)非負(fù), 且允許f關(guān)于ξ,η超線性或次線性增長(zhǎng)的條件下, 利用不動(dòng)點(diǎn)指數(shù)理論獲得了BVP(1)正徑向解的存在性結(jié)果.但對(duì)于球域該結(jié)果并不成立.事實(shí)上, 文獻(xiàn)[5]給出了一個(gè)典型的例子:
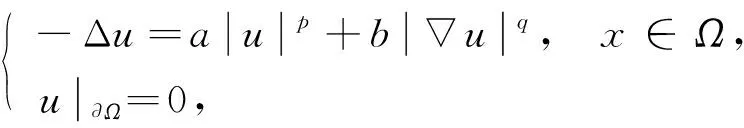
(2)
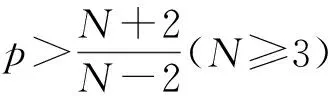
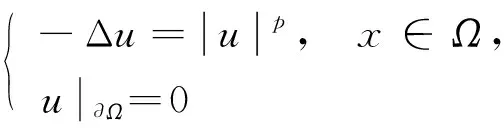
(3)
沒(méi)有正徑向解.此時(shí), BVP(3)為BVP(2)中a=1,b=0的特例.因此, BVP(2)在球域上無(wú)正徑向解.研究球域上橢圓邊值問(wèn)題徑向解的存在性比環(huán)域及球外部區(qū)域上的橢圓邊值問(wèn)題徑向解的存在性更復(fù)雜.目前, 關(guān)于球域上BVP(1)徑向解的存在性結(jié)果研究報(bào)道較少.文獻(xiàn)[8]用上下解方法研究了單位球上BVP(1)正徑向解的存在性, 在非線性項(xiàng)f滿足適當(dāng)?shù)牟坏仁綏l件下, 獲得了BVP(1)正徑向解的存在性結(jié)果, 該不等式條件允許f(r,ξ,η)關(guān)于ξ和η負(fù)向超線性增長(zhǎng).本文研究單位球上橢圓BVP(1)徑向解的存在性與唯一性, 在允許f(r,ξ,η)關(guān)于ξ和η超線性增長(zhǎng)的條件下, 用Schauder不動(dòng)點(diǎn)定理給出BVP(1)徑向解及正徑向解的存在性結(jié)果, 并通過(guò)進(jìn)一步加強(qiáng)條件討論該問(wèn)題徑向解的唯一性.
1 預(yù)備知識(shí)
對(duì)橢圓邊值問(wèn)題(1)的徑向?qū)ΨQ(chēng)解u=u(|x|), 令r=|x|, 則其可轉(zhuǎn)化為區(qū)間I上的常微分邊值問(wèn)題(BVP):
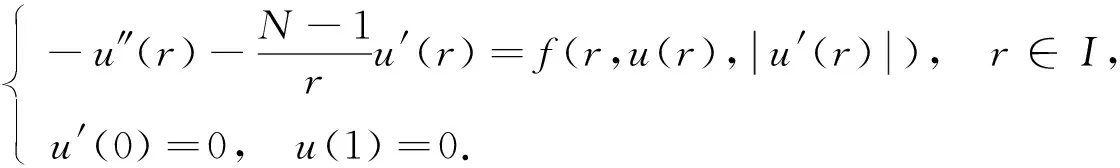
(4)
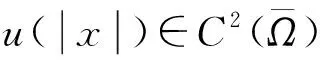
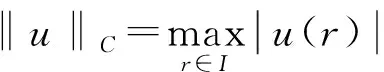
構(gòu)成的Banach空間.
為討論BVP(4), 先考慮相應(yīng)的二階線性邊值問(wèn)題(LBVP):
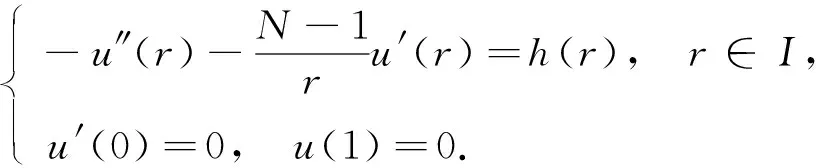
(5)
引理1[8]對(duì)?h∈C(I), LBVP(5)有唯一解u∶=Sh∈C2(I), 解算子S:C(I)→C1(I)為線性全連續(xù)算子, 且

(6)
由式(6), 易得

(7)
引理2對(duì)?h∈C+(I), 線性邊值問(wèn)題(5)的解u=Sh滿足u≥0,u′≤0.
證明: 將方程(5)兩邊同乘rN-1, 得
-(rN-1u′(r))′=rN-1h(r),r∈I.
(8)
對(duì)方程(8)兩邊積分, 再應(yīng)用方程(5)的邊界條件, 得
因此u(r)≥0,u′(r)≤0,r∈I.證畢.
記
其中R1,R2為正常數(shù), 則ΩR1,ΩR2為C1(I)中的凸閉集.
2 主要結(jié)果
假設(shè)條件:

|f(r,ξ,η)|≤R1, (r,ξ,η)∈I××+.
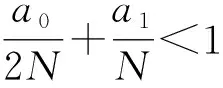
|f(r,ξ2,η2)-f(r,ξ1,η1)|≤a0|ξ2-ξ1|+a1|η2-η1|.
定理1設(shè)f:I××+→連續(xù).若f滿足條件(H1), 則BVP(1)至少有一個(gè)徑向解.
證明: 對(duì)?u∈ΩR1, 令
F(u)(r)∶=f(r,u(r),|u′(r)|),r∈I,
則F:ΩR1→C(I)連續(xù), 且將有界集映為有界集.定義映射A=S°F, 由引理1知,S:C(I)→ΩR1為線性全連續(xù)算子.因此, 算子A:ΩR1→ΩR1為線性全連續(xù)算子.由S的定義, BVP(4)的解等價(jià)于算子A的不動(dòng)點(diǎn).
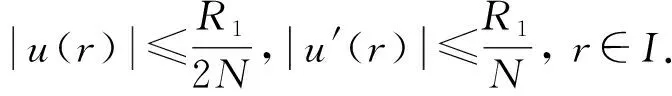
即A(ΩR1)?ΩR1.由Schauder不動(dòng)點(diǎn)定理知,A在ΩR1中有不動(dòng)點(diǎn).該不動(dòng)點(diǎn)為BVP(4)的解, 因此, BVP(1)有徑向解.證畢.
定理2設(shè)f:I××+→連續(xù).若f滿足條件(H2), 則BVP(1)有唯一徑向解.
證明: 先證存在性, (H2)?(H1).
令
(r,ξ2,η2)=(r,ξ,η), (r,ξ1,η1)=(r,0,0),
由條件(H2), 有

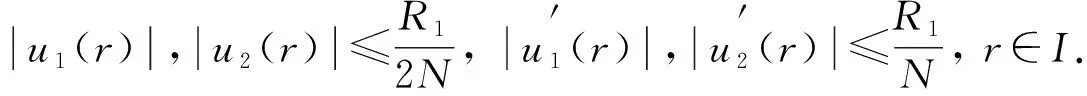
對(duì)式(9)兩端取‖·‖C, 得
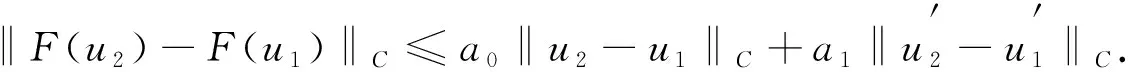
(10)
令u=u2-u1, 故
u=u2-u1=A(u2)-A(u1)=S(F(u2)-F(u1))=Sh.
由S的定義,u為h=F(u2)-F(u1)∈C(I)相應(yīng)LBVP(5)的解.因此, 由式(6)及式(10), 得
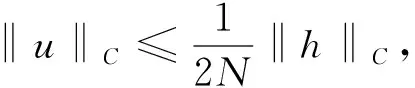
(11)

(12)

(13)
將式(11)乘a0, 由式(13), 得
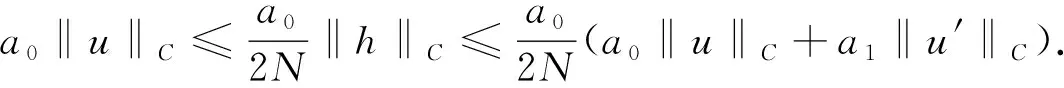
(14)
將式(12)乘a1, 由式(13), 得
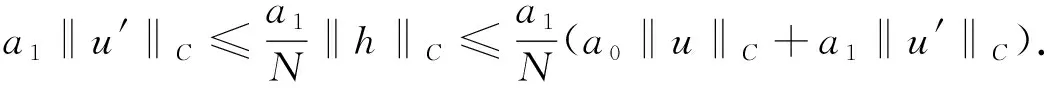
(15)
由式(13)~(15), 有
所以
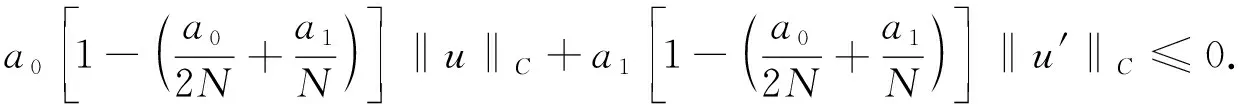
(16)
在定理1和定理2中, 非線性項(xiàng)f(r,ξ,η)關(guān)于ξ,η可超線性增長(zhǎng).當(dāng)f(r,ξ,η)關(guān)于ξ,η均一次增長(zhǎng)時(shí), 有:
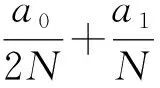
|f(r,ξ,η)|≤a0|ξ|+a1η+C, ?(r,ξ,η)∈I××+.
定理3設(shè)f:I××+→連續(xù).若f滿足條件(H3), 則BVP(1)至少有一個(gè)徑向解.


由引理2, LBVP(5)的解算子S為正算子.假設(shè)非線性項(xiàng)f非負(fù), 下面給出BVP(1)正徑向解的相關(guān)結(jié)果.

定理4設(shè)f:I×+×+→+連續(xù).若f滿足條件(H4), 則BVP(1)至少有一個(gè)正徑向解.
證明: 對(duì)?u∈ΩR2, 令
F(u)(r)∶=f(r,u(r),|u′(r)|),r∈I,
則F:ΩR2→C+(I)連續(xù), 且將有界集映為有界集.定義映射A=S°F, 由引理1知,S:C+(I)→ΩR2為線性全連續(xù)算子, 因此, 算子A:ΩR2→ΩR2為線性全連續(xù)算子.再由S的定義知, BVP(4)的解等價(jià)于算子A的不動(dòng)點(diǎn).
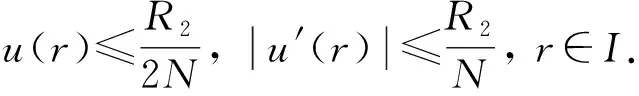
即A(ΩR2)?ΩR2.由Schauder不動(dòng)點(diǎn)定理知,A在ΩR2中有不動(dòng)點(diǎn).該不動(dòng)點(diǎn)為BVP(4)的正解, 因此, BVP(1)有正徑向解.證畢.
在定理4中, 非線性項(xiàng)f(r,ξ,η)關(guān)于ξ,η也可超線性增長(zhǎng).當(dāng)f(r,ξ,η)關(guān)于ξ,η均一次增長(zhǎng)時(shí), 有:
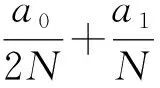
f(r,ξ,η)≤a0ξ+a1η+C, ?(r,ξ,η)∈I×+×+.
定理5設(shè)f:I×+×+→+連續(xù).若f滿足條件(H5), 則BVP(1)至少有一個(gè)正徑向解.
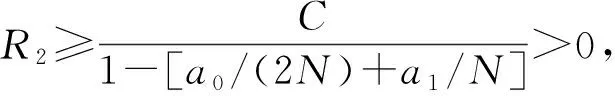
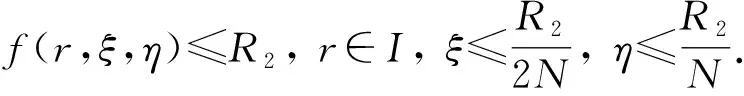
例1設(shè)N≥2, 考慮單位球Ω={x∈N: |x|<1}上含梯度項(xiàng)的橢圓邊值問(wèn)題:
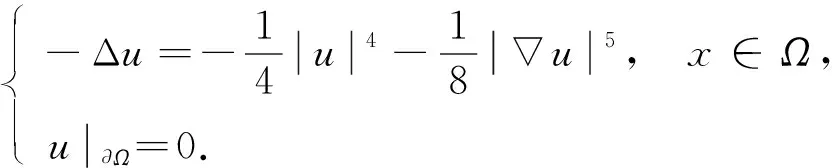
(17)
對(duì)應(yīng)于BVP(1), 相應(yīng)的非線性項(xiàng)為
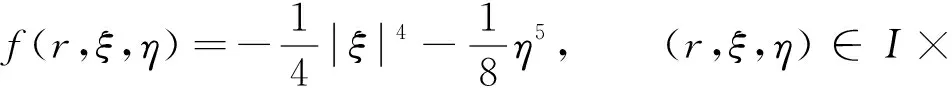
(18)
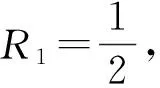
即?R1>0, 使得f(r,ξ,η)滿足條件(H1).因此由定理1知, BVP(17)有徑向解.
例2設(shè)N≥2, 考慮單位球Ω={x∈N: |x|<1}上含梯度項(xiàng)的橢圓邊值問(wèn)題:
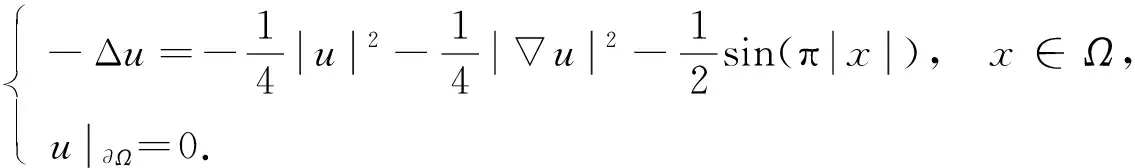
(19)
對(duì)應(yīng)于BVP(1), 相應(yīng)的非線性項(xiàng)為
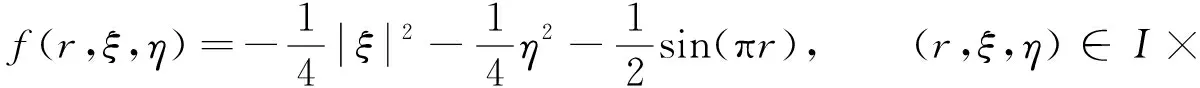
(20)
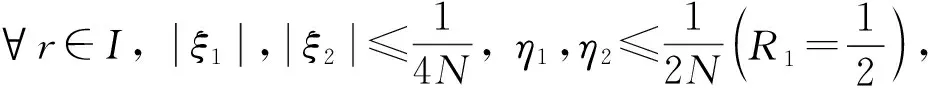
由式(20), 有
因此由式(21), 有
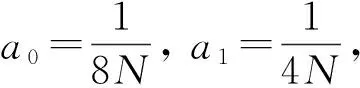
 吉林大學(xué)學(xué)報(bào)(理學(xué)版)2021年5期
吉林大學(xué)學(xué)報(bào)(理學(xué)版)2021年5期
- 吉林大學(xué)學(xué)報(bào)(理學(xué)版)的其它文章
- 《吉林大學(xué)學(xué)報(bào)(理學(xué)版)》征稿簡(jiǎn)則
- 前驅(qū)粉體低溫?zé)Y(jié)溫度與壓強(qiáng)對(duì)SDC電解質(zhì)電學(xué)性能的影響
- 基于光纖干涉原理的轉(zhuǎn)機(jī)監(jiān)測(cè)振動(dòng)傳感器設(shè)計(jì)
- 時(shí)間尺度上約束Hamilton系統(tǒng)的Noether對(duì)稱(chēng)性和守恒量
- 二維函數(shù)光子晶體中的類(lèi)Dirac點(diǎn)及帶隙結(jié)構(gòu)
- 基于卷積神經(jīng)網(wǎng)絡(luò)的超聲造影圖像去噪方法
