一類植物-草食動物擴散系統的動力學分析
麻曉琦, 趙治濤
(黑龍江大學 數學科學學院, 哈爾濱 150080)
0 引 言
捕食模型在構建生物群落、 促進物種進化以及保護生物多樣性等方面具有重要作用, 目前已得到廣泛關注[1-5]. 經典的捕食者-食餌模型中, 食餌多以Logistic形式增長, 但自然界中的一些食餌并不符合上述規律, 如植物經常表現出抗食草性, 植物的根部不容易被捕食, 或者種子不能被消化等. 于是, 一些研究者提出了食餌具有抗食草性的捕食模型[6-13], 即食餌增長時, 總有一部分不能被捕食者捕食, 該部分仍能繼續生長成完整植株. 這種防御機制更符合實際.
植物與草食動物之間的相互作用是生態學、 進化生物學和資源管理等領域的研究熱點. Feng等[6]認為植物可通過補償性再生長恢復被草食動物損失的生物量, 進而提出利用可食用和可被草食動物獲取的生物量進行建模, 分析植物-草食動物群落的種群變化; Agrawal[7]研究了植物具有防御性時對環境的適應能力及其未來的進化趨勢, 進而影響系統的生物多樣性; Nalam等[8]指出因為植物地下生物量(種子, 根部)可很快地再生成完整植株, 因此根作為合成防御化合物的主體, 發揮著抗草食動物的作用; Mortensen等[9]指出了Logistic模型的不足, 并提出將再生模型和Logistic模型相結合, 考慮植物種間競爭因素對種群的影響.
本文考慮如下一類再生模型和Logistic模型相結合的植物-草食動物擴散系統的動力學性質:

(1)
其中N表示植物在地表上的生物量,P表示草食動物的生物量,R表示植物在地表下的生物量或根部,r表示植物的內稟增長率,a表示草食動物的捕食率,K表示環境最大容量,c表示草食動物的營養轉換效率,d表示草食動物的死亡率,d1,d2分別表示植物和草食動物的擴散系數,n為邊界?Ω上的單位外法向量,α和β為正常數. 首先, 討論系統(1)解的長時間性質, 包括解的全局存在性、 耗散性和持續性; 其次, 分析系統(1)常值穩態解的存在性、 局部漸近穩定性和全局漸近穩定性, 并給出系統(1)圖靈不穩定的判別準則; 最后, 通過數值模擬驗證所得結果的有效性.
1 解的長時間性質
下面討論系統(1)解的長時間性質, 包括解的全局存在性、 耗散性和持續生存.
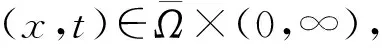
證明: 首先, 注意到系統(1)在區域{N≥0,P≥0}上是一個混擬單調系統.令
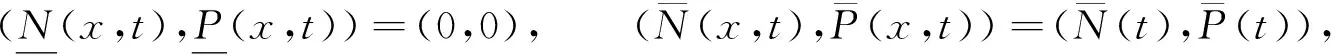
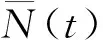
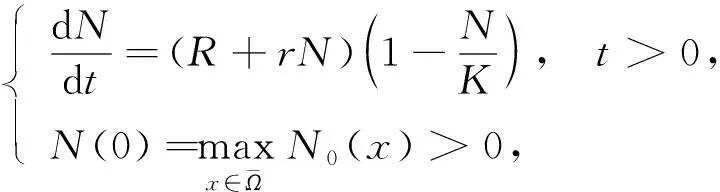
(2)
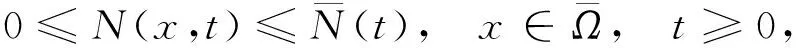
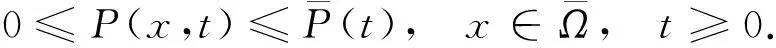
定理2設(N(x,t),P(x,t))是系統(1)的任意解, 則有
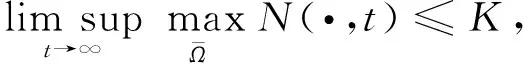
(3)
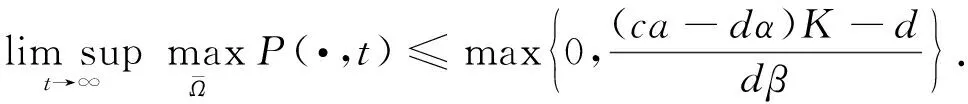
(4)
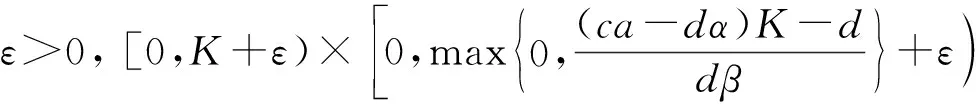
證明: 因為N(x,t)滿足
設z(t)是下列初值問題
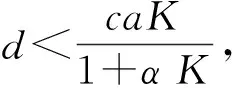
再由ε的任意性可得
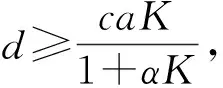
同理, 可得
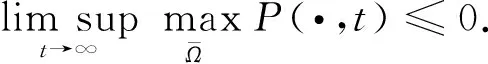
因此式(4)成立.證畢.
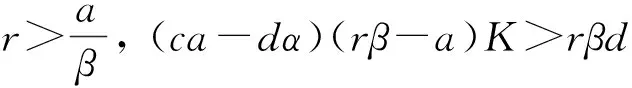
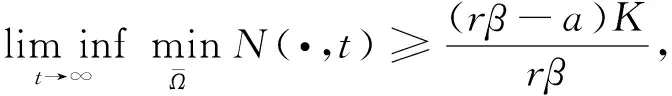
(5)
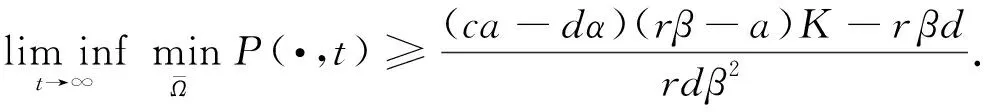
(6)
即系統(1)是持續生存的.
證明: 由系統(1)的第一個方程, 有
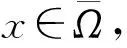
設w(t)是初值問題
的唯一正解.因為(ca-dα)(rβ-a)K>rβd, 所以存在充分小的ε>0, 使得
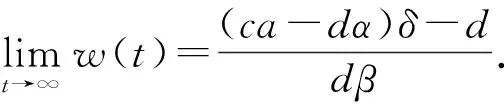
2 常值穩態解的存在性與穩定性
系統(1)的常值穩態解有E1=(K,0)和E2=(N*,P*), 其中(N*,P*)滿足
經簡單計算可得
令
易得

因此當d<(ca-dα)N*時, 系統(1)有唯一的正常值穩態解.
設算子-Δ在Ω上具有齊次Neumann邊界條件的特征值為
μi∈Λ?{μi: 0=μ0<μ1<…<μi<…,i∈}.
設S(μi)是特征值μi對應的特征子空間,m(μi)是特征值μi的重數, {φij|1≤j≤m(μi)}是S(μi)的一組標準正交基.記
則
其中(φ,ψ)∈X, 且
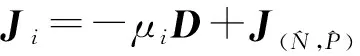
λ2-Tiλ+Di=0,i∈
的解, 其中
Ti=-μi(d1+d2)+a11+a22,
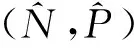
首先, 考慮常值穩態解E1=(K,0)的穩定性.
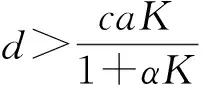
證明: 通過簡單計算可得
于是, 系統(1)在E1處線性化系統對應的特征方程為
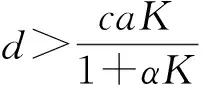
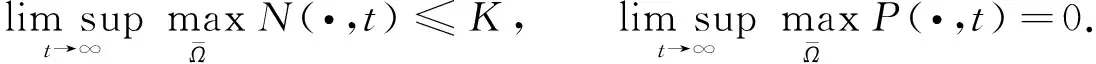
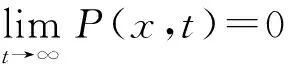
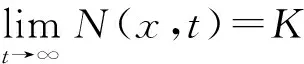
其次, 討論常值穩態解E2=(N*,P*)的穩定性.
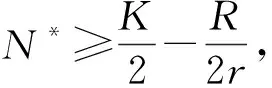
證明: 由d<(ca-dα)N*可知E2存在.經簡單計算有
其中
于是, 系統(1)在E2處線性化系統對應的特征方程為
λ2-Tiλ+Di=0,i∈,
其中
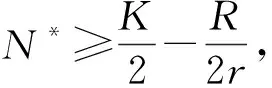
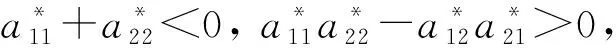

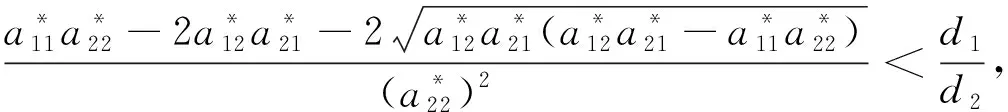
(7)
則E2是局部漸近穩定的.
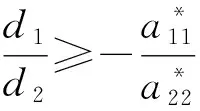
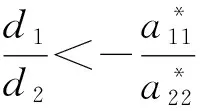
成立, 則有
表明對任意的i∈, 均有Di>0.又因為
于是當式(7)成立時, 對任意的i∈, 均有Di>0.因此E2是局部漸近穩定的.證畢.
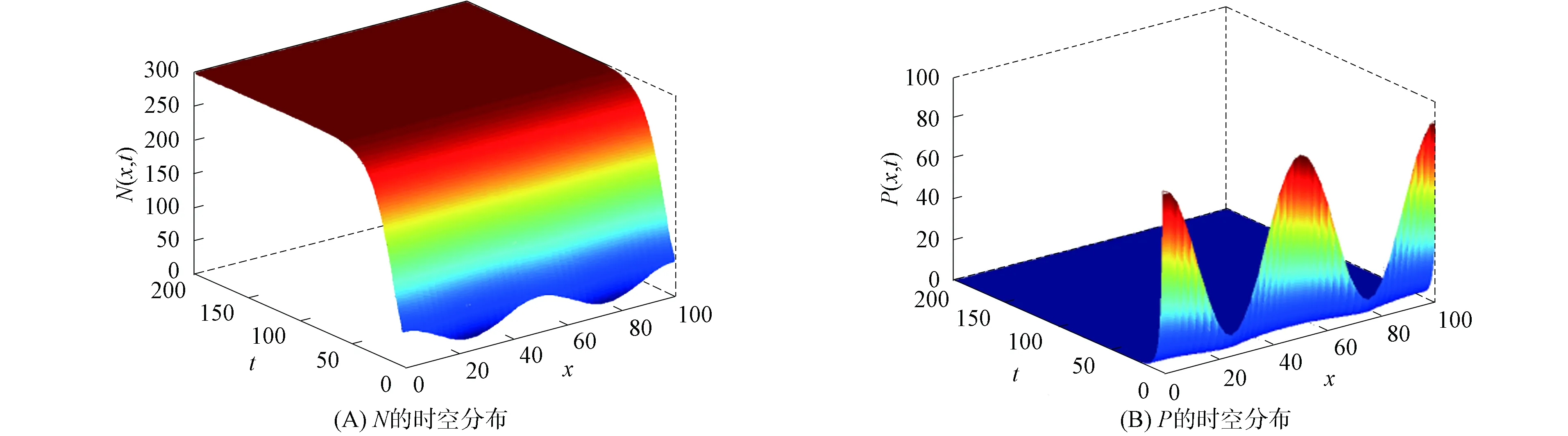
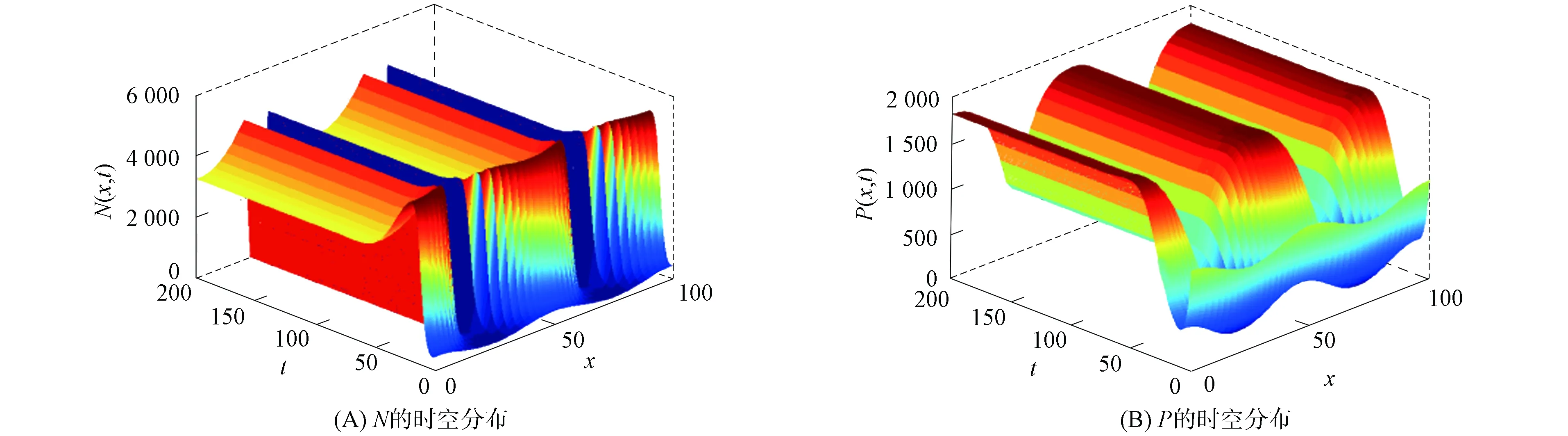
定理7設d<(ca-dα)N*, 如果(caαK-dα2K-rcβ)N* 證明: 定義Lyapunov函數為 沿系統(1)的解(N(x,t),P(x,t))計算其導數, 可得 其中 注意到(P-P*)2的系數小于0, (N-N*)2的系數滿足 最后, 考慮系統(1)在常值穩態解(N*,P*)處的圖靈不穩定性[14].圖靈不穩定性也稱為擴散驅動不穩定性, 是指在無擴散作用時系統穩定, 但在擴散作用下當滿足某些條件時系統不穩定, 從而導致非均勻的空間分布. (8) 成立, 則方程 有兩個正根: 3) 對固定的d2>0, 存在d*>0, 使得當0 證明: 1)和2)顯然成立. 3) 對固定的d2>0, 有 下面利用MATLAB進行數值模擬, 以驗證本文所得常值穩態解的相關結果.固定R=10,K=300,r=0.06,a=0.033,c=0.8,α=0.06,β=0.4,d1=1,d2=1.取d=0.5, 則 于是定理4的條件成立.圖1為邊界穩態解E1的分布.由圖1可見, 常值穩態解E1=(300,0)是全局漸近穩定的, 表明定理4成立.取d=0.4, 則 (ca-dα)N*=0.695 7, (caαK-dα2K-rcβ)N*=6.957 1,dαK=7.200 0, 于是定理7的條件成立.圖2為正常值穩態解E2的分布.由圖2可見, 常值穩態解E2=(289.879 5,1.848 2)是全局漸近穩定的, 即定理7成立. 圖1 邊界穩態解E1Fig.1 Boundary steady state solution E1 取R=2,K=6 000,r=0.6,a=0.033,c=0.8,α=0.05,β=0.03,d1=0.01,d2=10, 則 于是定理8的條件成立.圖3為正非常值穩態解的分布.同理由圖3可見, 定理8成立. 圖3 正非常值穩態解Fig.3 Positive nonconstant steady state solution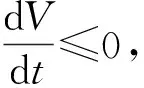
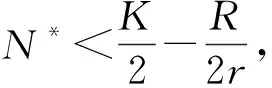

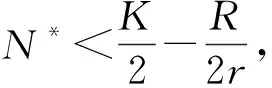
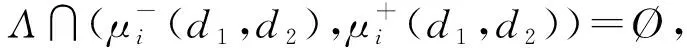
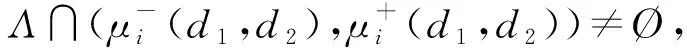
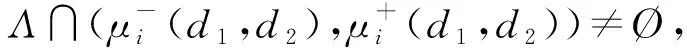
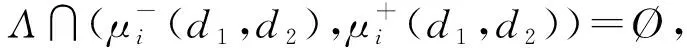
3 數值模擬