帶有加性噪聲的阻尼吊橋方程隨機吸引子的存在性

馬文君, 孫亮亮

(1. 蘭州工商學院 經濟學院, 蘭州 730101; 2. 西北師范大學 數學與統計學院, 蘭州 730070)

0 引 言

自Lazer等[1]提出并研究了如下吊橋方程的大振幅周期振蕩問題

以來, 關于吊橋方程解的存在性和行波解性質的研究已有很多結果[2-4]. 近年來, 隨著自然界中隨機干擾或不確定因素對確定性系統的影響, 關于隨機動力系統的研究也得到廣泛關注[5-9], 例如, Crauel等[7]對非線性擴散方程、 Navier-Stokes方程、 非線性波方程等證明了其隨機吸引子的存在性. 但在實際應用中, 吊橋系統不可避免地受隨機噪聲的影響. 本文考慮如下帶有加性噪聲的吊橋方程：

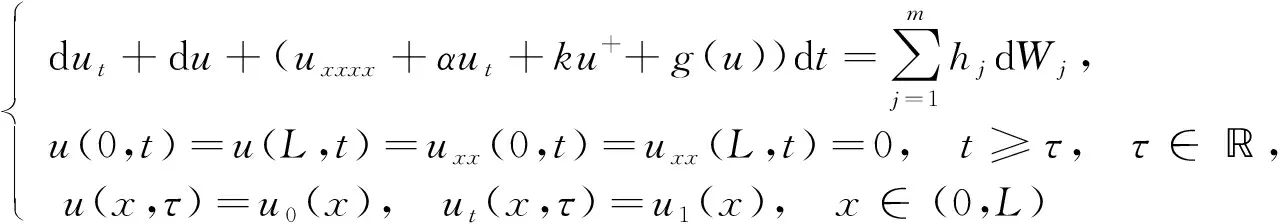
(1)

隨機吸引子的存在性, 其中: (x,t)∈(0,L)×[τ,+∞);u=u(x,t)表示橋面在豎直方向的振動,u+為其正部, 即

k>0表示彈性系數,ku+是橋面在垂直方向振動時由Hooke定律得到的恢復力.根據Hooke定律, 當吊橋被拉長時, 橋梁將受到大小與位移成正比的恢復力作用;α是黏性阻尼系數; 對任意的s∈, 非線性函數g∈C2(,)滿足下列假設:

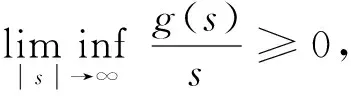
(2)

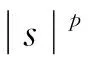
(3)

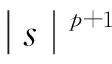
(4)

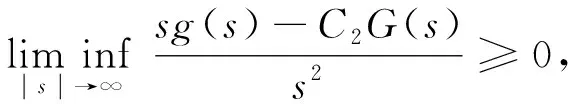
(5)

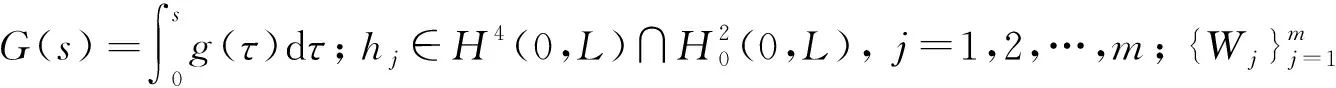
Θ={ω=(ω1,ω2,…,ωm)∈C(,m):ω(0)=0}

被賦予緊的開拓撲, P是相應的Wiener測度, F是Θ上的Borelσ-代數.記W(t,ω)∶=ω(t), 且定義

θtω(·)=ω(·+t)-ω(t),t∈,ω∈Θ.

文獻[10]研究了帶有加性噪聲的隨機強阻尼Plate方程隨機吸引子的存在性; 文獻[11]討論了帶白噪聲的可拉伸吊橋方程隨機吸引子的存在性; 文獻[12]研究了帶線性記憶和弱阻尼的問題(1)拉回吸引子的存在性. 但對帶有加性噪聲的隨機吊橋方程(1)解的漸近行為研究目前尚未見文獻報道. 由于當系統受到加性噪聲干擾時, 狀態空間的有界子集不再保持不變， 為建立系統的漸近緊性帶來困難. 因此, 研究帶有加性噪聲的隨機吊橋方程(1)隨機吸引子的存在性有一定的理論意義. 本文討論帶有加性噪聲的阻尼吊橋方程(1)解的漸近行為, 用算子分解技巧, 通過對方程的解進行先驗估計, 給出隨機動力系統的一致漸近緊性, 從而證明方程(1)隨機吸引子的存在性.

1 預備知識

設(X,‖·‖X)是一個具有Borelσ-代數B(X)的可分的Hilbert空間, D是X上所有調和隨機集的集合, (Θ,F,P,(θt)t∈)是一個度量動力系統.

定義1[5]設(Θ,F,P,(θt)t∈)是一個度量動力系統, 對于映射φ:+×Ω×X→X, 若其為(B(+)×F×B(X),B(X))-可測的, 且對所有的s,t∈+,x∈X和ω∈Θ均滿足下列條件:

1)φ(0,ω)x=x;

2)φ(s,θtω)°φ(t,ω)x=φ(s+t,ω)x.

則稱φ為隨機動力系統(RDS).進一步, 如果對于t≥0,ω∈Θ,φ關于x是連續的, 則稱φ為連續隨機動力系統.

定義2[5]如果隨機集A∶={A(ω)}ω∈Θ∈X滿足下列條件, 則稱A為隨機動力系統φ的D-隨機吸引子:

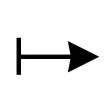
2) A是φ-不變的, 即對所有的T≥0及a.e.ω∈Θ,φ(t,ω,A(ω))=A(θtω);

3) A吸引所有調和隨機集B∈D, 即對所有的a.e.ω∈Θ, 有

其中dist(·,·)表示X中兩個子集之間的Hausdorff半距離.

命題1[5]設φ是X中關于(Θ,F,P,(θt)t∈)的連續隨機動力系統, 若存在一個隨機緊集K(ω), 使得對任意非隨機有界集{B(ω)}ω∈Θ, 有

則φ存在一個D-隨機吸引子A={A(ω)}ω∈Θ, 其中

2 解的存在唯一性

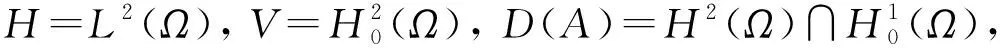
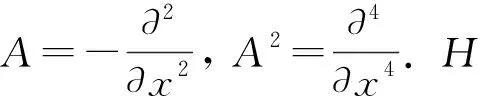
顯然有V?H=H*?V*, 其中H*,V*分別是H,V的對偶空間.

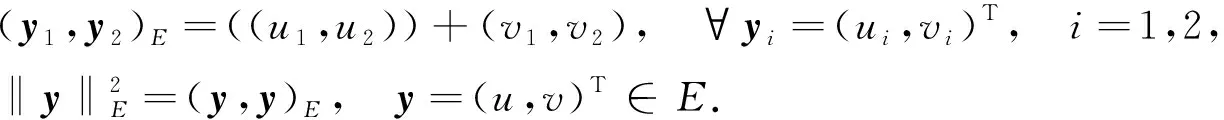
(6)

此外,Lp(Ω)范數記為‖·‖p.由Poincaré不等式, 得

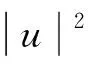
其中λ1是一個正常數.

為將問題(1)轉化為帶有隨機參數的確定性系統, 并證明其可生成一個隨機動力系統.下面考慮Ornstein-Uhlenbeck方程

dzj+zjdt=dWj(t),j={1,2,…,m}

(7)

和Ornstein-Uhlenbeck過程

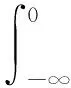
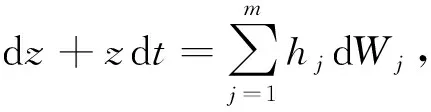
(8)

則

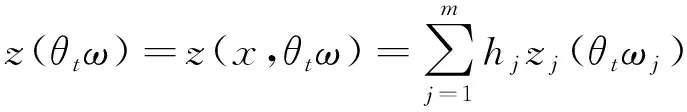
(9)

是式(8)的一個解.

‖z(θtω)‖≤eε|t|r(ω), e-ε|t|r(ω)≤r(θtω)≤eε|t|r(ω),

‖A(l)z(θtω)‖≤eε|t|r(l)(ω), e-ε|t|r(l)(ω)≤r(l)(θtω)≤eε|t|r(l)(ω),

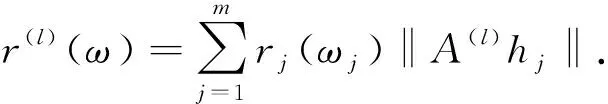
將方程(1)轉化為

(10)

設

可得方程(10)的矩陣形式：

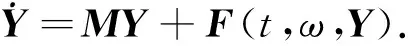
(11)

設φ1=u,φ2=v-z(θtω), 方程(10)可轉化為如下等價系統：

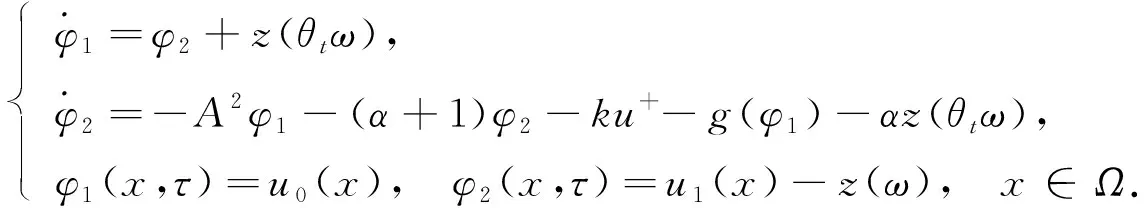
(12)

設φ=(φ1,φ2)T, 可得

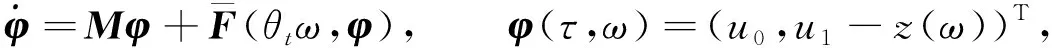
(13)

其中

由文獻[15]可知, -M是E上的C0-半群e-Mt的無窮小生成元, 且函數F(·,ω):E→E關于φ局部Lipschitz連續.所以, 由文獻[15]中發展方程解的局部存在唯一性經典半群理論, 可得隨機偏微分方程(13)有唯一解, 例如, 對a.s.φ(τ,ω)∈E, 有

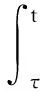
對a.e.ω∈Θ,T>0, 下列結論成立:

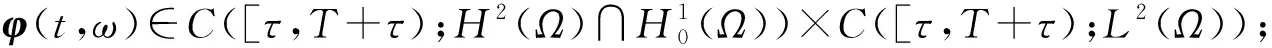
(ii)φ(t,φ(τ,ω))關于t和φ(τ,ω)連續;

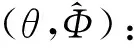
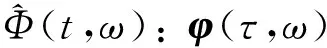
(14)

因此, 通過變換

(15)

也可生成一個與方程(10)相應的隨機動力系統.

3 隨機吸引子的存在性

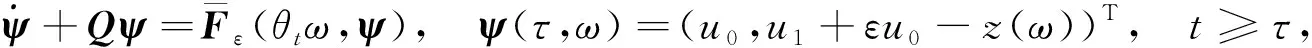
(16)

其中

定義映射

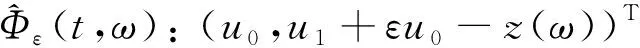
則

(17)

設υ(t)=(υ1,υ2)T=(u(t),v(t)+εu(t))T是系統(13)的解, 則式(13)可化為

υt+Qυ=G(θtω,υ),υ(-τ,ω)=(u0,u1+εu0)T,t≥τ,

(18)

其中

下面證明算子Q在E中的正定性.

引理2對任意的υ=(υ1,υ2)T∈E, 有

證明: 因為Qυ=(ευ1-υ2,(A2-ε(α-ε+1))υ1+(α-ε+1)υ2)T, 由Poincaré不等式可得

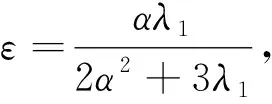
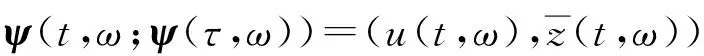
‖ψ(-1,ω;ψ(τ,ω))‖E≤r0(ω),τ≤T(B).

(19)

且對τ≤t≤0,

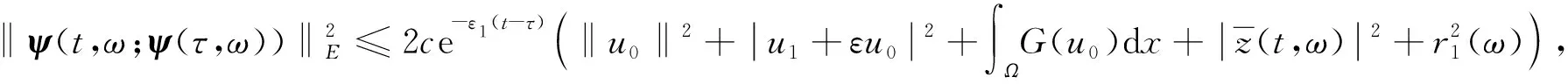
(20)

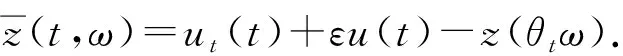
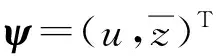
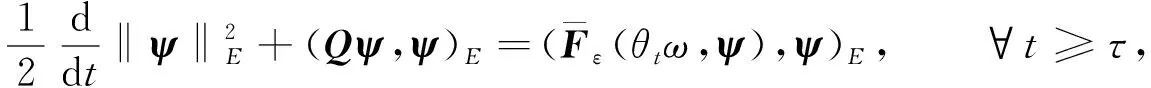
(21)

其中

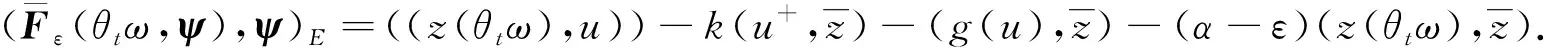
(22)

由Cauchy-Schwarz不等式和Young不等式, 有

(23)

(24)

(25)

結合式(3)～(5), 可得

故?M1>0, 使得

(27)

由式(26),(27), 得

由式(21),(23)～(25),(28)和引理2, 得

利用引理1, 有

其中

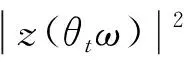
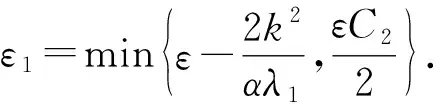
由引理1, 有

其中

令

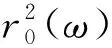
證畢.

為得到正則性估計, 本文利用文獻[8,16-17]中的方法, 將系統(1)的解u(t)分解成u=y1+y2, 分別滿足下列方程:

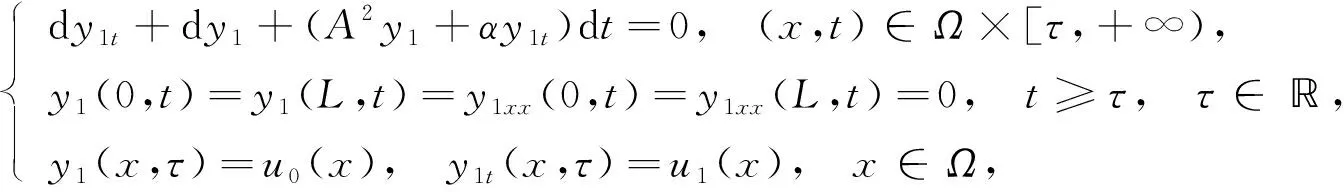
(30)

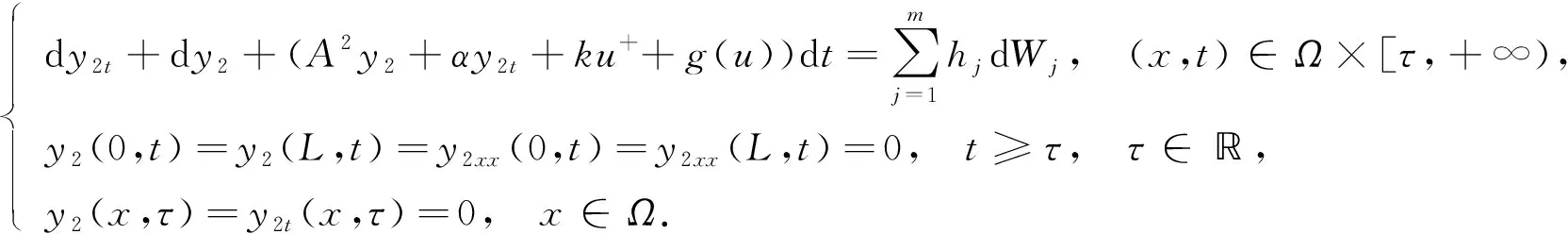
(31)

下面對方程(30)和方程(31)的解進行先驗估計.

引理4設B是E上的非空有界子集, 若條件(2)～(5)成立, 則對任意的(u0,u1+εu0)T∈B, 有

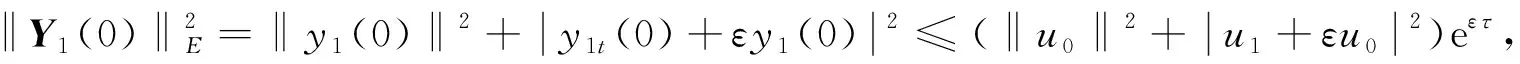
(32)

并存在一個隨機半徑r2(ω)>0, 使得對P-a.s.ω∈Θ, 有

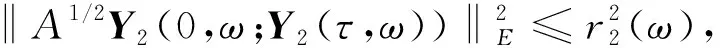
(33)

其中Y1=(y1,y1t+εy1)T和Y2=(y2,y2t+εy2-z(θtω))T分別滿足方程(30)和方程(31).

證明： 用初值為(u0,u1+εu0)T的y1t+εy1與方程(30)在L2(Ω)上做內積.由引理2可得式(32).下面證明式(33), 從而可得解(y2,y2t)更高的正則性.設Y2=(y2,y2t+εy2-z(θtω))T, 方程(31)可轉化為

Y2t+QY2=H(Y2,ω),Y2(τ)=(0,-z(ω))T,t≥τ,

(34)

其中

用AY2與方程(34)在E上做內積, 得

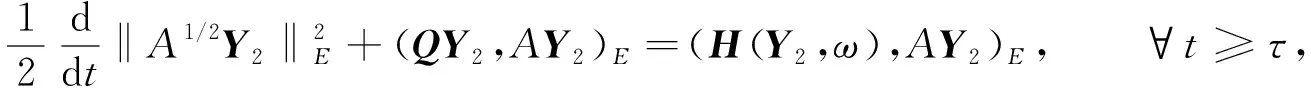
(35)

其中

由引理2可知,

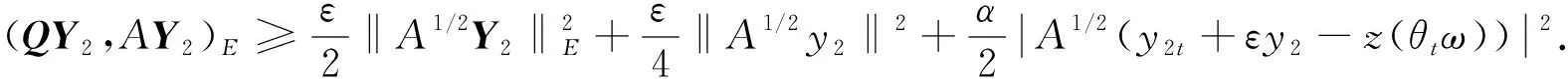
(37)

下面對式(35)右邊的各項進行如下估計:

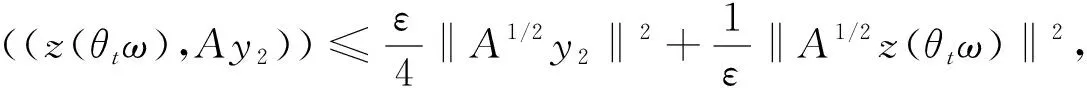
(38)

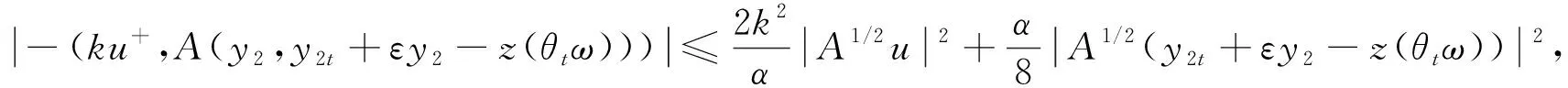
(39)

由式(3),(20)及Sobolev嵌入定理知,g′(u)在L∞上一致有界, 即存在常數M2>0, 使得

|g′(u)|L∞≤M2.

(41)

由Young不等式和式(41), 得

其中Cs>0是一個嵌入常數.

結合式(35)～(42),(20), 對所有的τ≤T(B), 均有

由Gronwall引理和引理1可得

令

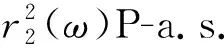
證畢.

從而有

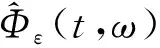
dist(Φε(t,θ-tω)B,B1/2(ω))→0, P-a.s.

因此, 由式(15)所確定的隨機動力系統Φε(t,ω)有一致漸近緊的吸引集B1/2(ω)∈E, 即隨機動力系統Φε(t,ω)在E中一致漸近緊.

定理1假設式(2)～(5)成立, 則式(15)所確定的隨機動力系統Φε(t,ω)有一個非空緊的D-隨機吸引子A.

證明: 結合引理3、 引理4及命題1可知結論成立.