序約束下單向分類方差分析模型的Bayes變量選擇

史海芳, 李 聰, 姬永剛

(1. 中國民航大學 理學院, 天津 300300; 2. 吉林大學 數學學院, 長春 130012)

在劑量反應實驗中, 時間可作為解釋變量, 人們可能在收集數據前就已獲得了潛在參數滿足序約束的先驗信息. 將這些先驗信息應用到統計推斷中可以提供更有效的估計, 特別是在具有低信噪比的小樣本情形下. 文獻[1-2]對序約束統計方法進行了全面闡述.

目前, 利用Bayes方法解決約束條件下的統計推斷問題已取得許多成果. 文獻[3]借助Savage-Dickey密度比方法[4]討論了序約束下單向分類方差分析(ANOVA)模型的假設檢驗問題, 利用該方法可近似計算各潛在的假設Bayes因子, 并選擇后驗概率最大的假設作為最優假設； 文獻[5]將該方法推廣到其有不等式約束條件的廣義線性模型中, 但Savage-Dickey密度比方法需要在每次Markov鏈Monte Carlo(MCMC)迭代中都近似計算標準正態分布的密度和分布函數值, 計算時間較長； 文獻[6-7]通過引進指標變量, 并假設指標變量與參數相互獨立, 分別將文獻[8]中的方法應用到單向分類和雙向分類方差分析模型中, 考慮了序約束下的變量選擇問題, 其優點是沒有過多的調節參數, 但文獻[9]指出若參數先驗分布的假設太模糊, 則可能會導致Markov鏈收斂較慢; 文獻[10-11]提出了另一種常用的Bayes變量選擇方法SSVS(stochastic search variable selection)方法, 目前SSVS已被擴展到很多模型和應用中, 例如遺傳數據分析[12]、 向量自回歸模型[13]和分組約束模型[14]等. 該方法的缺點是需要進行調節的參數較多. 為解決上述問題, 文獻[15]提出了一種改進的SSVS方法----NMIG(normal mixture of interse Gamma distributions)方法, 并將其應用到基因分析中. 本文將這兩種SSVS方法推廣到單向分類方差分析模型中， 并考慮序約束下的變量選擇問題. 基于MCMC方法引入指標變量, 計算潛在模型的后驗概率.

1 再參數化ANOVA模型中的變量選擇

令

yij=μi+εij,j=1,2,…,ni,i=1,2,…,k

(1)

表示一個單向ANOVA混合模型, 其中yij表示第j個個體第i次治療的反映變量,μi表示第i次治療的平均效應,εij表示誤差項且εij～N(0,σ2).實際應用中一般有如下幾種序約束：

(i) 簡單半序約束μ1≤…≤μk;

(ii) 簡單樹序約束μ1≥μi,i=2,…,k-1;

(iii) 傘序約束μ1≤…≤μg≥μg+1≥…≥μk, 其中g已知.

對于簡單半序約束μ1≤…≤μk, 如果令δm-1=μm-μm-1(2≤m≤k), 則第二個均值μ2可表示為μ1+δ1, 第三個均值可表示為μ1+δ1+δ2,…, 第m個均值(2≤m≤k)可表示為μ1+δ1+…+δm-1,μm的簡單序約束可等價地表示為δm的非負約束δm≥0,m=1,2,…,k-1.如果令δ=(δ1,δ2,…,δk-1), 則滿足簡單半序約束的模型(1)可表示為

y=1nμ1+xδ+ε,δ1≥0, …,δk-1≥0,

(2)

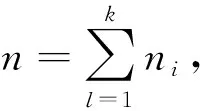
這里1m和0m分別表示元素皆為1和0的m×1維列向量.若均值滿足簡單樹序約束或傘序約束, 則本文也可定義相應的設計矩陣x及再參數化向量參數θ.這些不等式約束可參見文獻[3,5].盡管本文給出的方法適用于任何可表示為模型(2)的參數約束, 但為方便, 本文主要考慮簡單半序約束.

為能同時進行變量選擇和參數估計, 本文考慮兩種Bayes變量選擇方法： SSVS方法[10-11]和NMIG方法[15]. 本文將SSVS方法擴展到帶有序約束條件的單向ANOVA模型中.引入指示變量γi, 并假設γi和δi滿足下列先驗分布:

δi|γi,φi～TN(0,c(γi)φi,0,+∞),

(3)

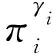
(4)

其中:

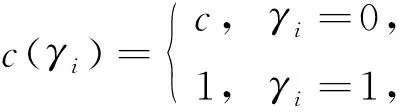
(5)

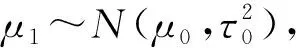
π(σ2)∝1,

文獻[16]將該先驗分布應用于無約束線性模型的變量選擇問題中.

上述先驗和超先驗分布對于其各自參數和超參數均為共軛的, 因此利用Gibbs抽樣方法易得參數的后驗分布.下面分別給出這兩種方法所有參數的滿條件分布.

1.1 SSVS方法

1)σ2的條件后驗分布.由于

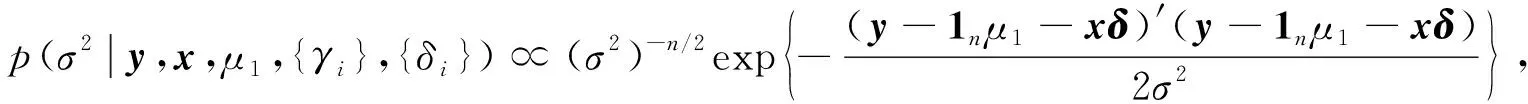
(6)

因此

σ2|y,x,μ1,{γl},{δl}～IGamma(n/2-1,(y-1nμ1-xθ)′(y-1nμ1-xθ)/2).

2)μ1的滿條件后驗分布.由于

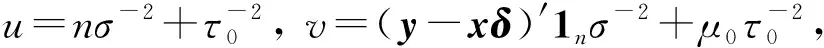
3)γi的滿條件后驗分布.令γ-i=(γ1,…,γi-1,γi+1,…,γq), 可證明γi的滿條件分布服從如下Bernoulli分布:

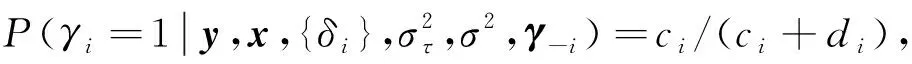
(7)

其中

ci=f(y|{δi},σ2,γi=1,γ-i)f(δi|γi=1,γ-i)f(γi=1,γ-i),

di=f(y|{δi},σ2,γi=0,γ-i)f(δi|γi=0,γ-i)f(γi=0,γ-i).

4)πi的滿條件后驗分布.由πi和γi的先驗可計算πi的后驗分布為

πi|y,x,{βi},σ2,{γi},μ1～Beta(a1+γi,b1-γi+1).

5)δp的滿條件后驗分布.由于

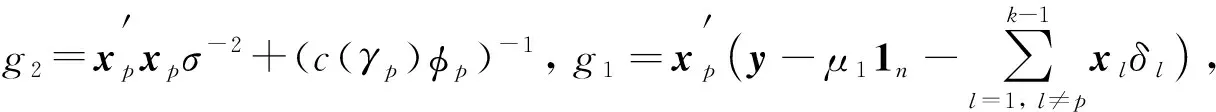
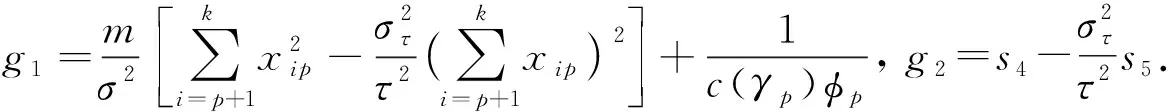
1.2 NMIG方法

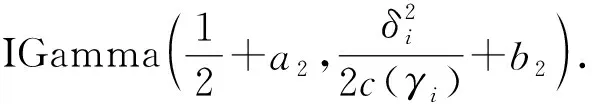
2 數值模擬

下面用數值模擬驗證本文方法的有效性, 并與文獻[3]和文獻[6]提出的方法進行對比, 將這兩種對比方法分別簡記為Oh方法[3]和Otava方法[6]. 假設k=4, 且均值滿足簡單半序約束, 則有下列8個備選模型：

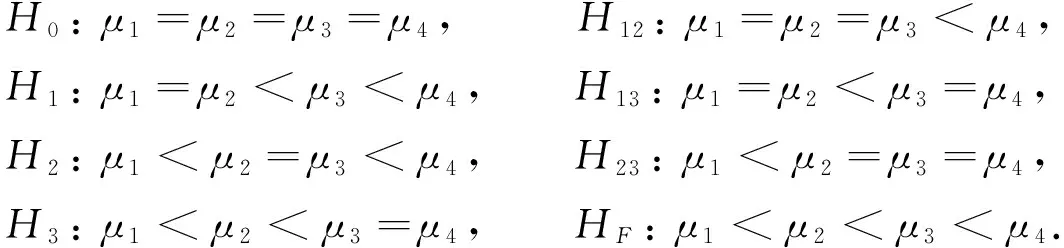
(8)

根據文獻[3], 假設誤差項服從獨立的標準正態分布, 考慮以下3種模擬:

模擬1:μ=(0,0,0,0)′; 模擬2:μ=(0,0,0,1)′; 模擬3:μ=(1,2,3,4)′.

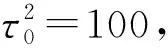
設樣本個數n=10,30,100, 每次產生10 000個Gibbs樣本, 為保證收斂, 丟棄前面的3 000個抽樣值.每種固定效應和樣本個數的取值都重復500次.表1～表3列出了所有模型的平均后驗概率.其中標*處對應真實模型的后驗概率.

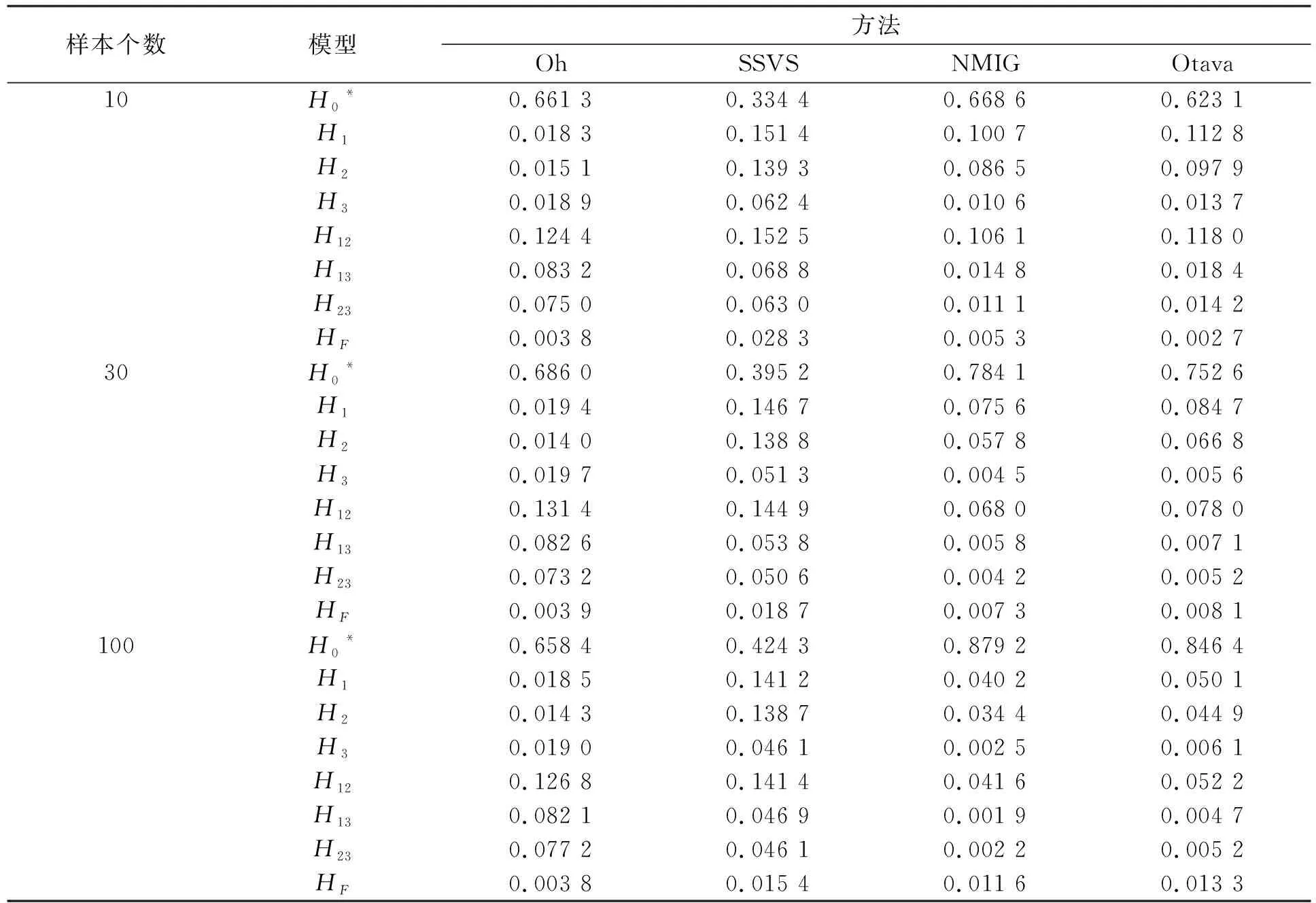
表1 模擬1中不同方法所得模型的平均后驗概率

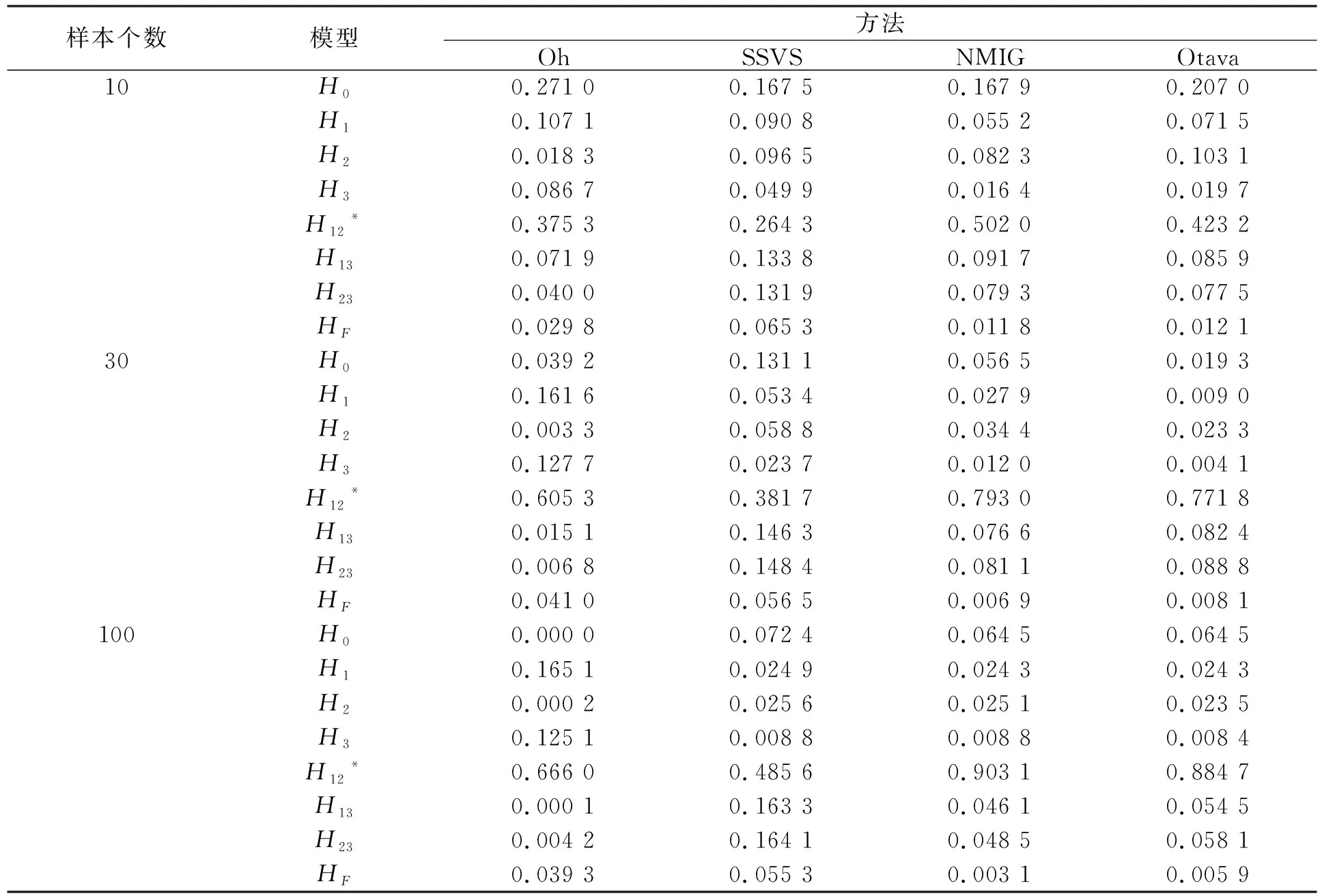
表2 模擬2中不同方法所得模型的平均后驗概率

表3 模擬3中不同方法所得模型的平均后驗概率

由表1～表3可見, 4種方法給出的真實模型后驗概率均為最大. 一般地, NMIG和Otava比其他兩種方法更傾向于提供真實模型更高的平均后驗概率. 為評價這些方法在識別正確模型方面的效果, 類似傳統假設檢驗的優勢, 本文計算了每種方法選擇正確模型的頻率P, 結果列于表4～表6. 由表4～表6可見, 在模擬3中Oh方法效果更好, 但在模擬1和模擬2中另外3種方法的正確模型識別率更高. 數值模擬結果表明, 在多數情形下, NMIG方法比SSVS方法效果更好, 這可能是因為在假設參數φi服從Gamma分布的條件下調節參數比固定其為常數更好.

表4 模擬1中不同方法選擇正確模型的頻率

表6 模擬3中不同方法選擇正確模型的頻率

3 實例分析

下面用本文方法分析一組由文獻[3]分析的實際數據. 實驗人員在18個月內測量了20名男孩在8歲、 8.5歲、 9歲、 9.5 歲時的支骨高度(ramus bone heights). 令μ1,μ2,μ3，μ4分別表示4次觀測的平均支骨高度. 根據先驗信息, Oh方法假設平均支骨高度滿足簡單半序約束μ1≤μ2≤μ3≤μ4, 并利用Savage-Dickey密度比方法進行了分析. 本文利用SSVS方法和NMIG方法對該數據進行分析, 并與Oh方法和Otava方法進行比較.考慮式(8)模型H0～HF, 假設先驗的超參數取值與數值模擬相同, 并產生40 000個Gibbs樣本, 將前20 000個樣本作為初始值. 表7列出了所有模型的后驗概率. 由表7可見, NMIG方法和Otava方法選擇了相同的最大后驗模型, 同時4種方法均認為8.5歲時的平均支骨高度與9歲時的平均支骨高度有差異.表8和表9分別列出了參數δi(i=1,2,3)的后驗均值和可信區間.由表8和表9可見, Otava方法給出的后驗均值更大, 而SSVS方法給出了長度更短的Bayes可信區間, 表明SSVS方法在該數據集中表現較好. 圖1和圖2分別為SSVS方法和NMIG方法中參數δi(i=1,2,3)的后驗密度估計.由圖1和圖2可見, 兩種方法都很好地將參數δi(i=1,2,3)控制在非負區間上.

綜上所述, 本文討論了序約束下單向分類方差分析模型中的變量選擇問題, 提出了兩種基于SSVS方法序約束下的Bayes變量選擇方法, 并利用數值模擬和實例分析驗證了本文方法的有效性. 本文提出的后驗抽樣方法較簡單, 且易操作.

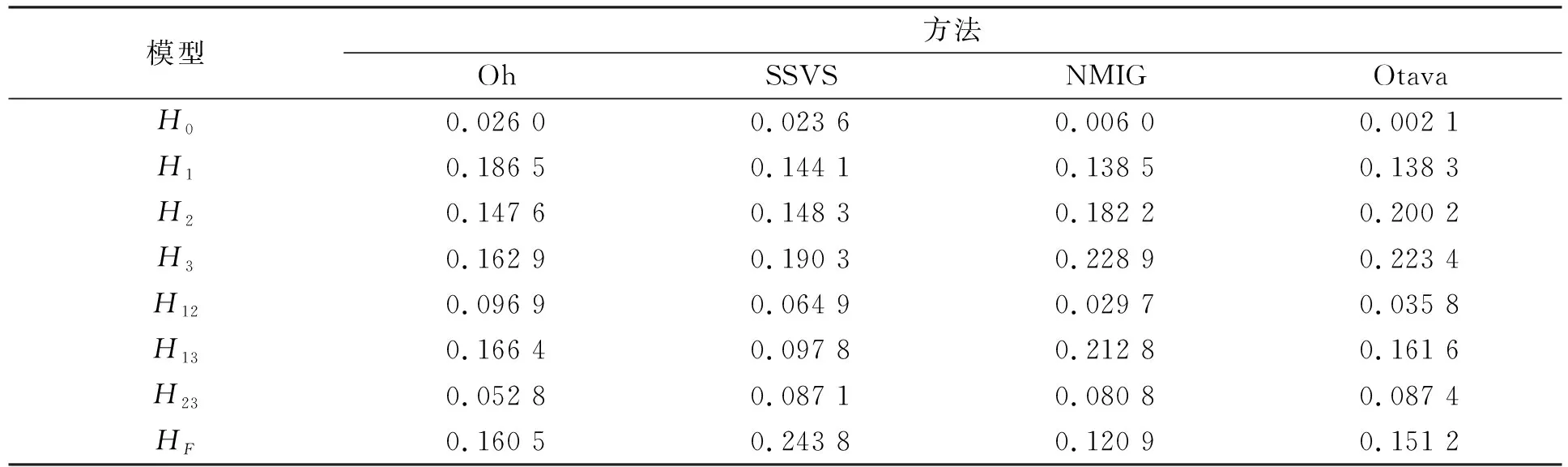
表7 支骨高度數據中模型的后驗概率

表8 支骨高度數據中參數的后驗均值

表9 支骨高度數據中參數的95%可信區間

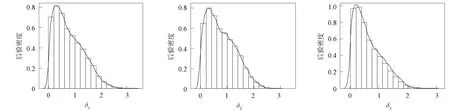
圖1 SSVS方法參數δ1,δ2,δ3的后驗密度估計Fig.1 A posteriori density estimation of parameters δ1,δ2,δ3 in SSVS method

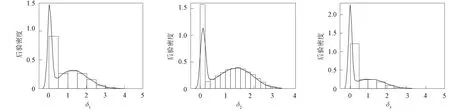
圖2 NMIG方法參數δ1,δ2,δ3的后驗密度估計Fig.2 A posteriori density estimation of parameters δ1,δ2,δ3 in NMIG method