一類多元Hermite型插值的離散化問題

姜 雪, 崔 凱

(1. 沈陽師范大學 數學與系統科學學院, 沈陽 110034; 2. 吉林大學 符號計算與知識工程教育部重點實驗室, 長春 130012)

多項式插值問題在圖像處理、 電子通信、 控制論和海洋氣象學等領域應用廣泛. 一元多項式插值理論包括插值函數的構造、 誤差分析、 最佳逼近性質等， 目前已有較完善的結果[1]. 但多元多項式插值問題的研究還不完善, 其中一個重要原因是多元插值節點的結構較復雜, 每個節點上對應的插值條件也有多種形態[2-6]. 一元Lagrange插值是最簡單的一類多項式插值, 其插值條件僅包含節點的函數值; 一元Hermite插值問題是指插值條件不僅包含節點處的函數值, 還包含節點處的連續階偏導數. 在多元情形下, 仍有Lagrange插值的概念, 但Hermite插值的定義卻不一致.

一元Hermite插值問題可視為Lagrange插值問題的極限形式. Shekhtman[7]證明了該結論在二元情形下也成立, 但對于三元及三元以上的情形, 總存在不能被離散的Hermite型插值問題. 類似于一元情形, 當多元Hermite型插值問題的插值條件僅由單項偏導條件構成時, 利用差分代替偏導數, 可將其離散為Lagrange插值問題的極限[8]. 目前, 關于Hermite型插值離散化問題的研究已有許多成果[9-14]. Hermite型插值離散化問題的實質是插值條件的離散. 本文將Hermite型插值問題轉化為Lagrange插值問題的極限, 從而將復雜的問題簡單化, 為構造復雜的多元插值問題的插值空間及給出誤差公式提供一種新思路.

1 預備知識

spanF{δz°q(D):z∈Z,q∈Qz}

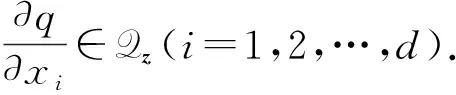
針對多元Hermite型插值問題, 如果每個節點對應的微分不變子空間誘導的微分算子均可以離散, 則該Hermite型插值問題可離散為Lagrange插值問題的極限.因此, 離散化問題可以逐點考慮.利用線性變換, 總可以假設插值節點z=0.對于任意給定單點的Hermite型插值問題, 設插值條件空間為

δ0°Q0(D)∶={δ0°q(D):q∈Q0}.

此外, 設有節點

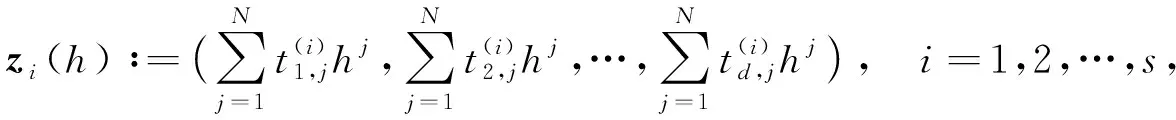
(1)

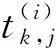
則zi(h)構成上述Hermite插值問題的離散節點.

對任意光滑的函數f,f(z(h))在0點的Taylor展開為

(2)

其中

pi為將式(2)視為h的多項式時hi的系數.對任意的正整數m, 令

基于上述記號, 文獻[12]給出了如下離散逼近算法.

輸入: 節點z=0, Qz=span{1,q1,q2,…,qs}, 其中deg(q1)≤deg(q2)≤…≤deg(qs);

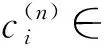
成立或“失敗”.

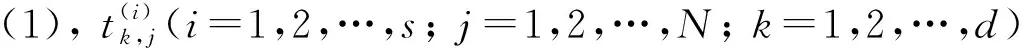
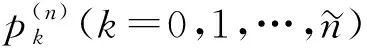
步驟3) 令

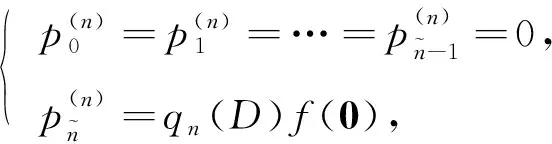
(3)

將式(3)確定的等式加入到S中, 置n∶=n+1;

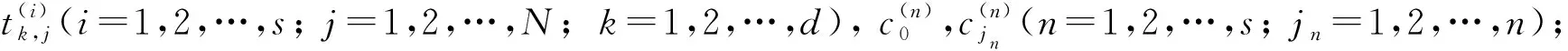
步驟5) 求解系統S, 若有解則選取S的一個特解, 并輸出離散節點及系數, 否則返回“失敗”, 算法終止.

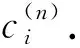
2 主要結果

由Q微分不變的性質可知, 1∈Q, 因此可假設Q基底中多項式不含常數項.對任意給定的二階微分不變子空間

其中上角標表示多項式的次數.不失一般性, 利用變量替換并約掉常數項, 則任意微分不變子空間Q中的一次多項式均可表示為

(4)

其中x∶=(x1,x2,…,xd).基于上述記號, 文獻[11]給出了二階微分不變子空間基底中二次多項式的形式:

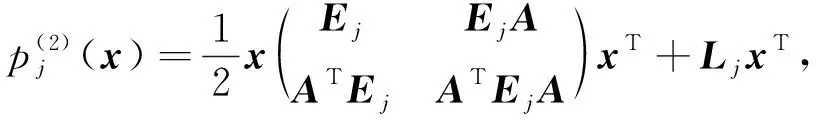
(5)

其中Ej為m1×m1對稱矩陣,

為一個行向量.

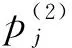
設節點z0(h)=0, 根據上述離散逼近算法可設空間Q對應下列離散節點:

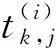
zi(h)=(ti,1h,ti,2h,…,ti,dh)=(ti,1,ti,2,…,ti,d)h,i=1,2,…,m+1.

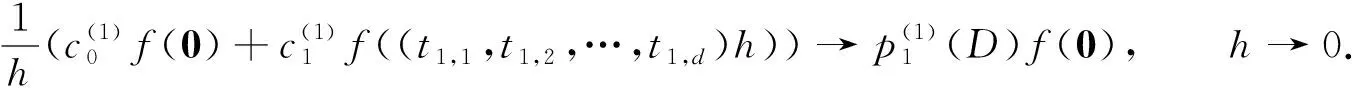
(6)

設

ek=(0,…,0,1,0,…,0)T∈Fm,k=1,2,…,m,

其中1位于第k個位置.記

ti=(ti,1,ti,2,…,ti,d),tih=(ti,1h,ti,2h,…,ti,dh),i=1,2,…,m+1,

則由式(2)可得

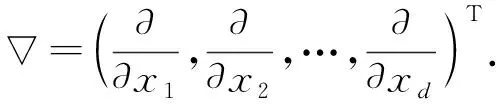
其等價于

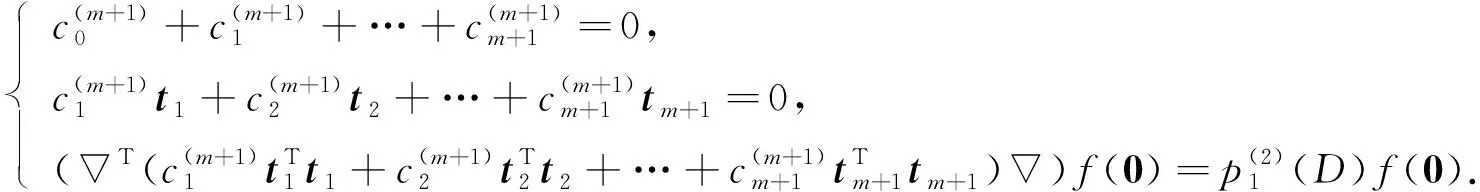
(7)

下面給出本文的主要結果.

定理2對任意給定的二階微分不變子空間

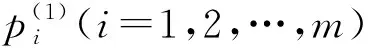
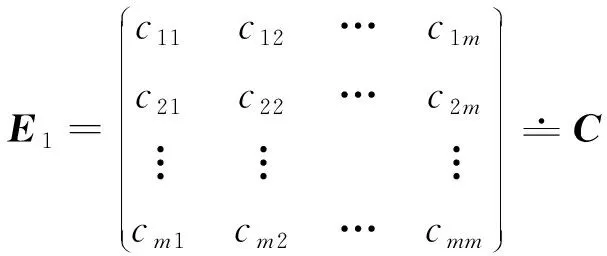
(8)

證明: 由上述分析可知, 在離散逼近算法思想下, 空間δ0°Q(D)可被離散的充分必要條件是下列方程組有解:

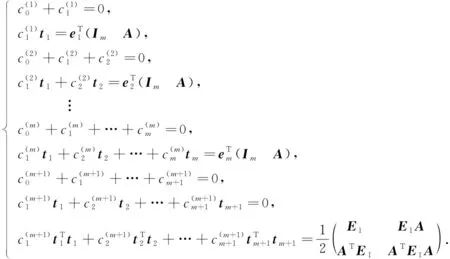
(9)

方程組(9)中最后一個等式成立是由定理1及

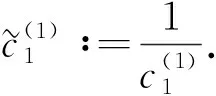
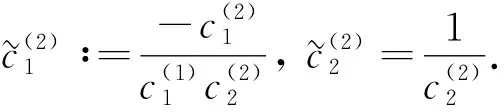
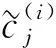
因此方程組(9)最后一個等式的左端為

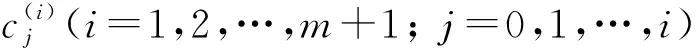
令其與式(9)右端相等可知結論成立.證畢.

推論1設有插值條件形如spanF{δz°q(D):q∈Qz}的Hermite型插值問題, 且Qz具有定理2所述形式, 若方程(8)有解, 則該Hermite型插值問題可寫成Lagrange插值的極限形式.

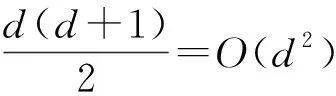
注2若所考慮插值問題對應的Qz基底中包含多個二次多項式, 則只需在方程組(9)中添加相應的等式再求解即可.

3 應用實例

定理2利用離散逼近算法的思想, 結合微分不變子空間的結構給出了二階微分不變子空間對應的Hermite型插值問題可以離散的充要條件. 文獻[11]由于事先確定了一階離散節點, 得到的只是該問題的充分條件. 考慮文獻[11]中的例3, 文獻[11]給出的方法無法計算出其離散節點, 但利用本文定理2可以計算得到其離散節點.

假設有Hermite型插值問題, 插值條件構成的空間為

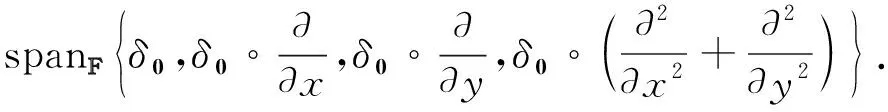
(10)

按本文理論,

Q=spanF{1,x,y,x2+y2},

根據定理2, 節點z0(h)=(0,0),zi(h)=(ti,1h,ti,2h)=(ti,1,ti,2)h(i=1,2,3)構成空間δ0°Q(D)一組離散節點的充要條件是下列關于參數ti=(ti,1,ti,2)(i=1,2,3)及組合系數的方程組有解:

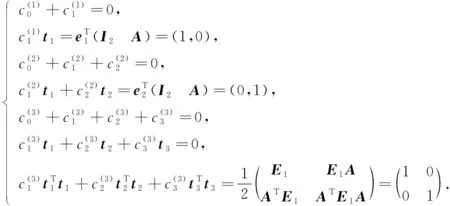
(11)

在MAPLE上求解方程組(11)并取其一組解, 可得離散節點:

z0(h)=(0,0),z1(h)=(h,0),z2(h)=(2h,2h),z3(h)=(2h,-5h),

即節點(0,0),(h,0),(2h,2h),(2h,-5h)上的Lagrange插值問題當h→0時收斂到插值條件形如式(10)的Hermite型插值問題.