阻尼結(jié)構(gòu)重頻特征靈敏度計(jì)算的擴(kuò)展Nelson方法

隋廣宇 , 李正光, 吳柏生

(1. 吉林大學(xué) 數(shù)學(xué)學(xué)院, 長春 130012; 2. 廣東工業(yè)大學(xué) 機(jī)電工程學(xué)院, 廣州 510006)

0 引 言

在航空、 航天、 機(jī)械、 建筑等許多工程領(lǐng)域, 結(jié)構(gòu)的固有頻率和模態(tài)振型關(guān)于設(shè)計(jì)變量或系統(tǒng)參數(shù)的導(dǎo)數(shù)信息, 即結(jié)構(gòu)特征靈敏度分析, 是CAE(computer aided engineering)分析的重要組成部分, 常用于求解結(jié)構(gòu)優(yōu)化設(shè)計(jì)、 模型修改、 系統(tǒng)控制和損傷探測等工程問題[1]. 目前, 已有多種計(jì)算特征靈敏度的分析方法, 如有限差分法、 模態(tài)法、 代數(shù)法、 迭代法和Nelson類方法等[2-3].

相對于無阻尼結(jié)構(gòu), 阻尼結(jié)構(gòu)更復(fù)雜且更能真實(shí)模擬現(xiàn)實(shí)結(jié)構(gòu), 其特征靈敏度分析也更有實(shí)際意義. 阻尼結(jié)構(gòu)的模態(tài)振型和頻率滿足二次特征值問題：

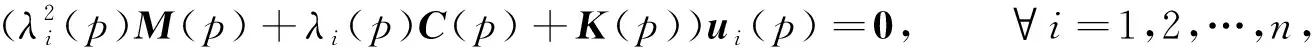
(1)

其中p為設(shè)計(jì)變量,M(p),K(p),C(p)是p的實(shí)對稱矩陣函數(shù), 分別為質(zhì)量矩陣、 剛度矩陣和阻尼矩陣,n為系統(tǒng)自由度個(gè)數(shù),ui為模態(tài)振型,λi為特征值.由于阻尼C(p)的存在, 因此特征值和模態(tài)振型是復(fù)數(shù)形式的.ω=Im(λi)/(2π)為阻尼圓頻率.對問題(1)進(jìn)行靈敏度分析, 主要有兩種策略： 第一種策略是引入狀態(tài)空間, 將原二次特征問題線性化, 轉(zhuǎn)換為狀態(tài)空間的一般廣義特征值問題, 然后利用廣義特征值靈敏度分析方法進(jìn)行求解[4], 但由于引入了狀態(tài)空間, 使問題的求解規(guī)模變?yōu)?n, 增大了問題的求解復(fù)雜度; 第二種策略是直接在n維空間進(jìn)行求解.Adhikari[5-6]分別根據(jù)狀態(tài)空間中的模態(tài)振型與頻率關(guān)系和無阻尼模態(tài)的性質(zhì)給出了n維空間上計(jì)算特征靈敏度的模態(tài)展開法; Li等[7]通過對模態(tài)法應(yīng)用Neumann級數(shù)展開技術(shù)減小了模態(tài)截?cái)嗟挠绊懀?Lee等[8]和Choi等[9]通過擴(kuò)展無阻尼結(jié)構(gòu)特征靈敏度分析中的代數(shù)方法, 利用加邊形式構(gòu)造出了模態(tài)靈敏度求解方程； Xie[10]提出了一種同時(shí)迭代方法求解阻尼結(jié)構(gòu)特征靈敏度. 上述方法都是針對孤立阻尼頻率的情形, 對于重頻情形, Wang等[11-12]擴(kuò)展了單頻情形下的特解求解方法, 給出了加邊形式及其改進(jìn)的特解求解方程, 但由于加邊的存在改變了原有矩陣的稀疏性, 增加了存儲和計(jì)算困難; Li等[13]采用組合正則條件的方法給出一種特解求解方法, 但特解方程的建立同樣采取了加邊形式.

Nelson方法[14]最初是針對標(biāo)準(zhǔn)特征值問題的孤立特征值靈敏度分析提出的, 其優(yōu)點(diǎn)是求解僅需所關(guān)心的頻率和模態(tài)振型信息, 不需要對矩陣行列進(jìn)行重排, 保持了原有矩陣的稀疏性. Cardani等[15]和Friswell等[16]擴(kuò)展了Nelson方法用于求解阻尼結(jié)構(gòu)的特征靈敏度分析, 但只適用于單頻問題； Ojalvo[17]和Dailey[18]發(fā)展了Nelson方法求解對稱廣義重特征值的特征靈敏度分析問題； Guedria等[19]發(fā)展了Nelson方法用于求解特征二階導(dǎo)數(shù)問題； Wu等[20]改進(jìn)了Nelson方法, 給出了一種構(gòu)造特解求解方程的方法, 用于求解重頻特征靈敏度問題, 但其只適用于無阻尼系統(tǒng).

針對阻尼結(jié)構(gòu)重頻復(fù)模態(tài)靈敏度計(jì)算問題, 本文提出一種新的擴(kuò)展Nelson方法. 通過構(gòu)造新的靈敏度特解控制方程, 并證明其系數(shù)矩陣的非奇異性, 擴(kuò)展了Nelson方法, 使其可以求解計(jì)算結(jié)構(gòu)重頻復(fù)模態(tài)靈敏度問題. 本文方法僅需利用重頻頻率對應(yīng)的模態(tài)振型, 無需擴(kuò)大方程求解規(guī)模和矩陣重排. 數(shù)值實(shí)例顯示了該方法的有效性.

1 擴(kuò)展Nelson方法

假設(shè)阻尼振動系統(tǒng)(1)在設(shè)計(jì)點(diǎn)p0存在m重頻率, 不妨令λi+1(p0)=λi+2(p0)=…=λi+m(p0)=λ,u1(p0),u2(p0),…,um(p0)是對應(yīng)的線性無關(guān)模態(tài)振型.相應(yīng)的二次特征值問題可以寫成矩陣形式：

M(p)U(p)Λ2(p)+C(p)U(p)Λ(p)+K(p)U(p)=0,

(2)

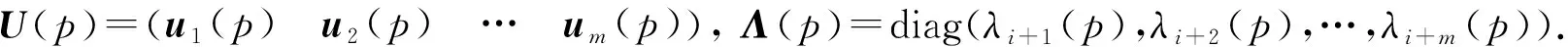
為保證特征向量的唯一性, 通常用下列正則條件：

UT(p)(2λ(p)M(p)+C(p))U(p)=Im,

(3)

其中Im是m階單位矩陣.顯然u1(p0),u2(p0),…,um(p0)的任意線性組合也是其特征向量, 并且一般情況下u1(p0),u2(p0),…,um(p0)不一定是可導(dǎo)的特征向量.記在p0處λi+1(p0)=λi+2(p0)=…=λi+m(p0)=λ的相應(yīng)可導(dǎo)特征向量為Z, 則有Z=UΓ, 其中Γ為m×m階正交矩陣.對可導(dǎo)的二次特征值問題：

M(p)Z(p)Λ2(p)+C(p)Z(p)Λ(p)+K(p)Z(p)=0,

(4)

關(guān)于設(shè)計(jì)變量p在p0點(diǎn)求導(dǎo)得

FZ′=G,

(5)

這里

F=λ2M+λC+K,G=-(2λM+C)ZΛ′-(λ2M′+λC′+K′)Z.

為書寫方便, 省略上述式中各矩陣函數(shù)p的表示, 有( )′表示p0處的導(dǎo)數(shù).對式(5)兩邊左乘UT并利用正則條件(3), 可得

EΓ=ΓΛ′,

(6)

其中E=-UT(λ2M′+λC′+K′)U.式(6)為m×m階標(biāo)準(zhǔn)特征值問題, 求解可得Γ和Λ′, 繼而得到可導(dǎo)特征向量Z.這里假設(shè)Λ′的各元素互異, 當(dāng)Λ′有重根時(shí), 需要考慮高階導(dǎo)數(shù)信息.

方程(5)是一個(gè)秩為n-m的奇異方程, 不能直接求解得到Z′, 本文擴(kuò)展Nelson方法, 將方程的解即特征向量導(dǎo)數(shù)表示為通解加特解形式, 即

Z′=V+Zc,

(7)

這里V是特解.特解V也滿足方程(5), 下面求該特解.將式(4)寫成如下形式：

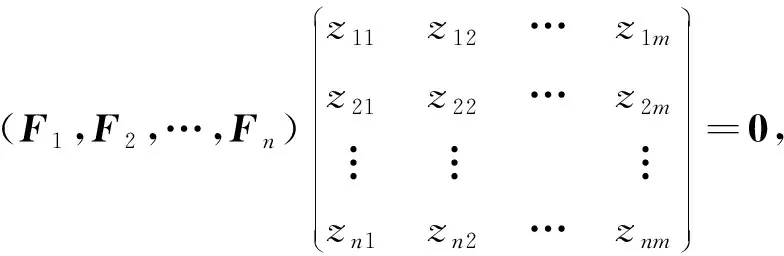
(8)

其中Fj(j=1,2,…,n)表示矩陣F的第j列.因?yàn)榫仃嘑的秩是n-m, 特征向量矩陣Z的秩是m, 所以可從Z中選擇m行得到一個(gè)m階的子塊Zm,m, 并使該子塊的行列式非零.不失一般性, 假設(shè)Z的前m行滿足上述條件, 即

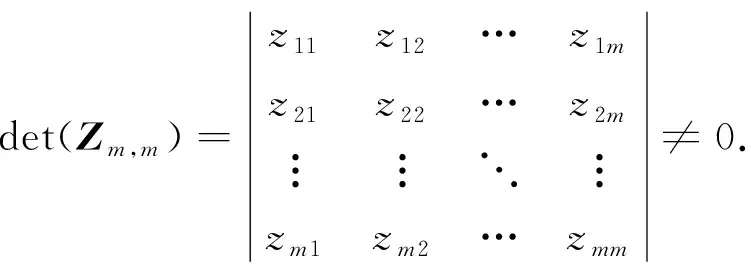
(9)

則式(8)可寫成下列形式：

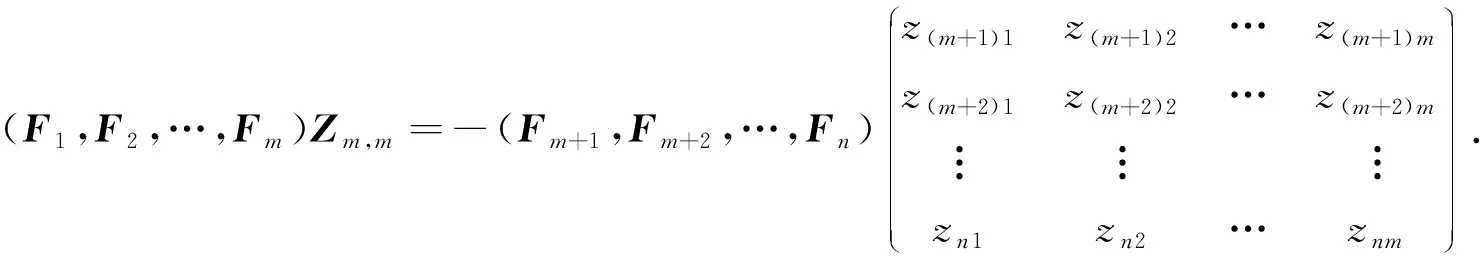
(10)

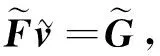
(11)

將ZT左乘方程(5)兩端得到ZTG=0, 進(jìn)而有

ZT(FV-G)=0.

(12)

將式(12)寫成分塊形式:

(13)

展開式(13)有

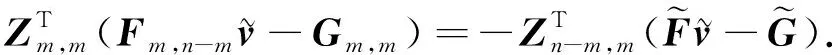
(14)

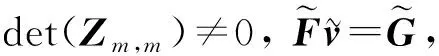
(15)

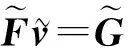
在實(shí)際計(jì)算特解V時(shí), 不需要將矩陣F刪去某些行列及重排, 只需根據(jù)Z選出一些行列, 將這些行列的非對角線元素設(shè)為零, 對角線元素不變即可, 這樣可以獲得較好的條件數(shù).相應(yīng)地, 將G的對應(yīng)行元素設(shè)為零即可.

對方程(5)關(guān)于設(shè)計(jì)變量p求導(dǎo), 有

將式(16)兩邊同時(shí)左乘ZT可得

將Z′=V+Zc代入式(17), 由規(guī)范化條件ZT(2λM+C)Z=Im得

對比式(18)兩邊, 當(dāng)i≠j時(shí), 有

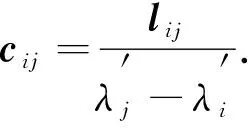
(19)

當(dāng)i=j時(shí), 對規(guī)范化條件ZT(2λM+C)Z=Im求導(dǎo), 代入Z′=V+Zc并應(yīng)用ZT(2λM+C)Z=Im, 得矩陣c的對角元為

cii=-0.5[ZT(2λM′+C′)Z-ZT(2λM+C)V-VT(2λM+C)Z]-ZTMZΛ′.

(20)

從而得到了系數(shù)矩陣c的所有元素, 將特解V與通解系數(shù)矩陣c代入式(7)即可得模態(tài)靈敏度Z′.

擴(kuò)展的Nelson方法求解阻尼結(jié)構(gòu)特征靈敏度分析步驟如下：

1) 求解方程(6), 由已知的特征模態(tài)計(jì)算可導(dǎo)的特征模態(tài)和特征值導(dǎo)數(shù)；

2) 從可導(dǎo)的特征向量矩陣Z中選擇一個(gè)m階的非奇異矩陣, 記錄所選擇的行數(shù)lj(j=1,2,…,m);

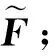
6) 利用式(19),(20)得到矩陣c；

7) 利用式(7)得到模態(tài)振型靈敏度Z′.

2 數(shù)值實(shí)驗(yàn)

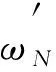
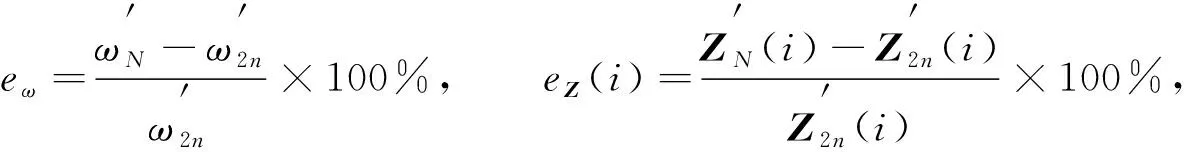
其中Z(i)表示向量Z的第i個(gè)分量.采用模態(tài)置信準(zhǔn)則[21]

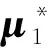
例1考慮如圖1所示帶有黏性阻尼的質(zhì)量彈簧系統(tǒng), 其中k=1 000 N/m,m=1 kg,c=10 N·s/m,k1=1 000 N/m. 系統(tǒng)的質(zhì)量矩陣M、 剛度矩陣K和阻尼矩陣C分別為

將剛度k作為設(shè)計(jì)參數(shù)p, 在p0=1 000 N/m點(diǎn)系統(tǒng)矩陣的導(dǎo)數(shù)分別為

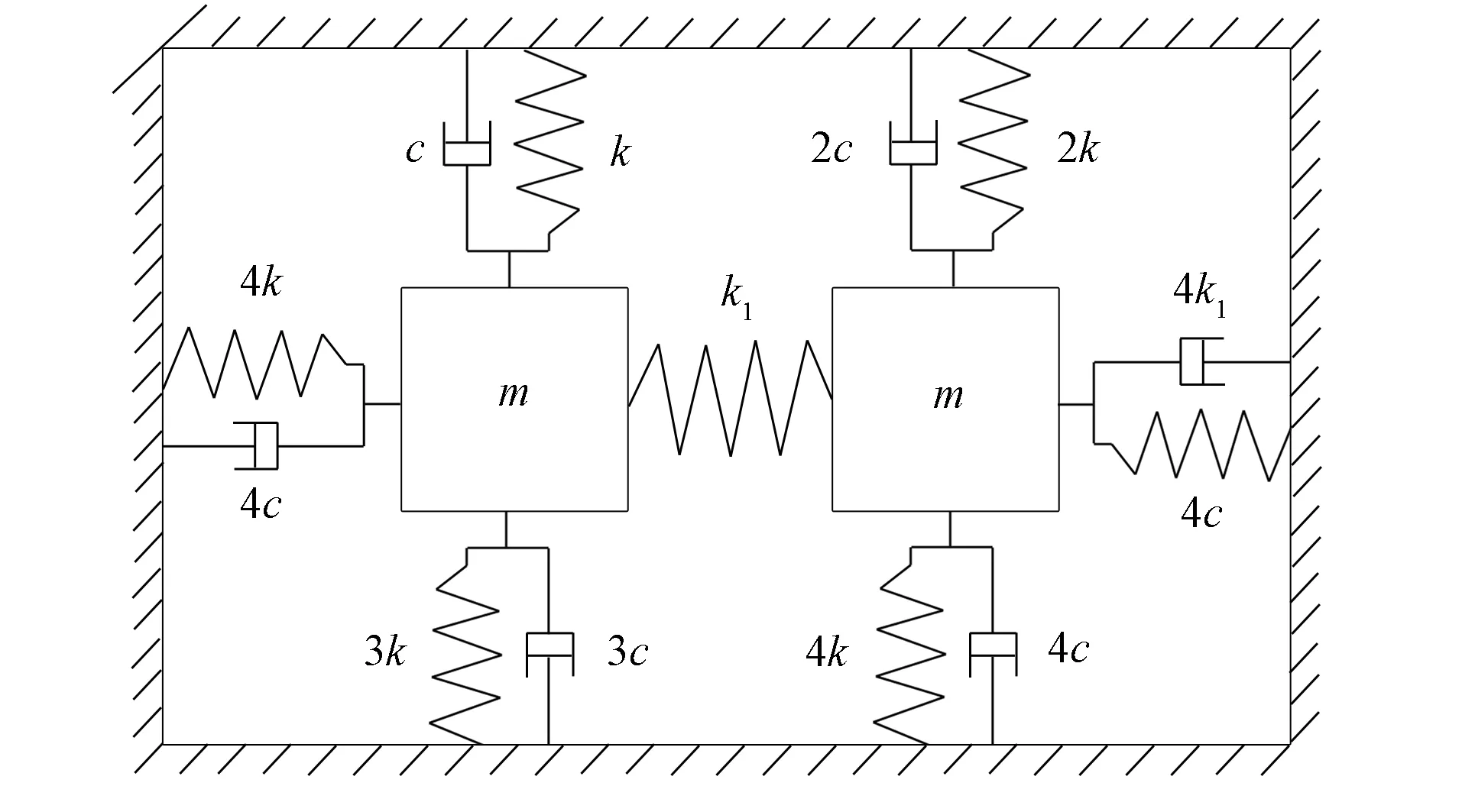
圖1 質(zhì)量彈簧阻尼系統(tǒng)Fig.1 Mass spring damped system

該系統(tǒng)有一個(gè)復(fù)重特征值

λ=-20.000 0+60.000 0i,

對應(yīng)的系統(tǒng)阻尼圓頻率ω=9.549 3 rad/s. 使用本文方法和2n空間線性化方法得到的頻率靈敏度列于表1, 兩個(gè)可導(dǎo)的模態(tài)及模態(tài)靈敏度分別列于表2和表3. 由表1～表3可見, 本文方法求解得到的頻率靈敏度誤差在計(jì)算機(jī)精度下達(dá)到0, 而模態(tài)振型靈敏度的各分量誤差也達(dá)10-13量級. 本文方法計(jì)算得到兩個(gè)可導(dǎo)模態(tài)振型的靈敏度與2n空間線性化方法得到的模態(tài)振型靈敏度MAC值均為1.0. 結(jié)果表明, 本文方法計(jì)算精度較高.

表1 質(zhì)量彈簧阻尼系統(tǒng)頻率靈敏度比較

表2 質(zhì)量彈簧阻尼系統(tǒng)可導(dǎo)模態(tài)振型1及其靈敏度比較

表3 質(zhì)量彈簧阻尼系統(tǒng)可導(dǎo)模態(tài)振型2及其靈敏度比較

例2考慮如圖2所示的由相同微結(jié)構(gòu)組成的一個(gè)平面桁架系統(tǒng), 該系統(tǒng)每個(gè)局部結(jié)構(gòu)均可視為由彈簧阻尼結(jié)構(gòu)組成, 其材料特性為： 材料密度ρ=7.8×103kg/m3, 彈性模量E=2.1×1011Pa, 阻尼系數(shù)c=100 N·s/m, 桿的截面積為A=0.1 m2.

考慮如圖3所示深色部分桿件的截面積為設(shè)計(jì)變量, 考慮其在A0=0.1 m2的圓頻率及模態(tài)振型靈敏度. 該結(jié)構(gòu)有一個(gè)重特征值λ=-2.258 1×10-4+3.672 5×102i, 對應(yīng)的圓頻率為58.449 9 rad/s. 使用本文方法和線性化策略計(jì)算圓頻率及圖2所示黑點(diǎn)處x方向自由度模態(tài)分量靈敏度, 結(jié)果列于表4～表6.由表4～表6可見, 本文方法求解得到的頻率靈敏度誤差在計(jì)算機(jī)精度下達(dá)10-8, 而特征模態(tài)振型靈敏度分量的誤差達(dá)10-6量級.本文方法計(jì)算得到兩個(gè)可導(dǎo)模態(tài)振型的靈敏度與2n空間線性化方法得到的模態(tài)振型靈敏度MAC值均為1.0. 結(jié)果表明, 本文方法計(jì)算精度較高. 本文方法的計(jì)算時(shí)間是0.015 2 s, 2n空間線性化方法的計(jì)算時(shí)間是0.0757 s, 本文方法的計(jì)算效率約為線性化方法的5倍.

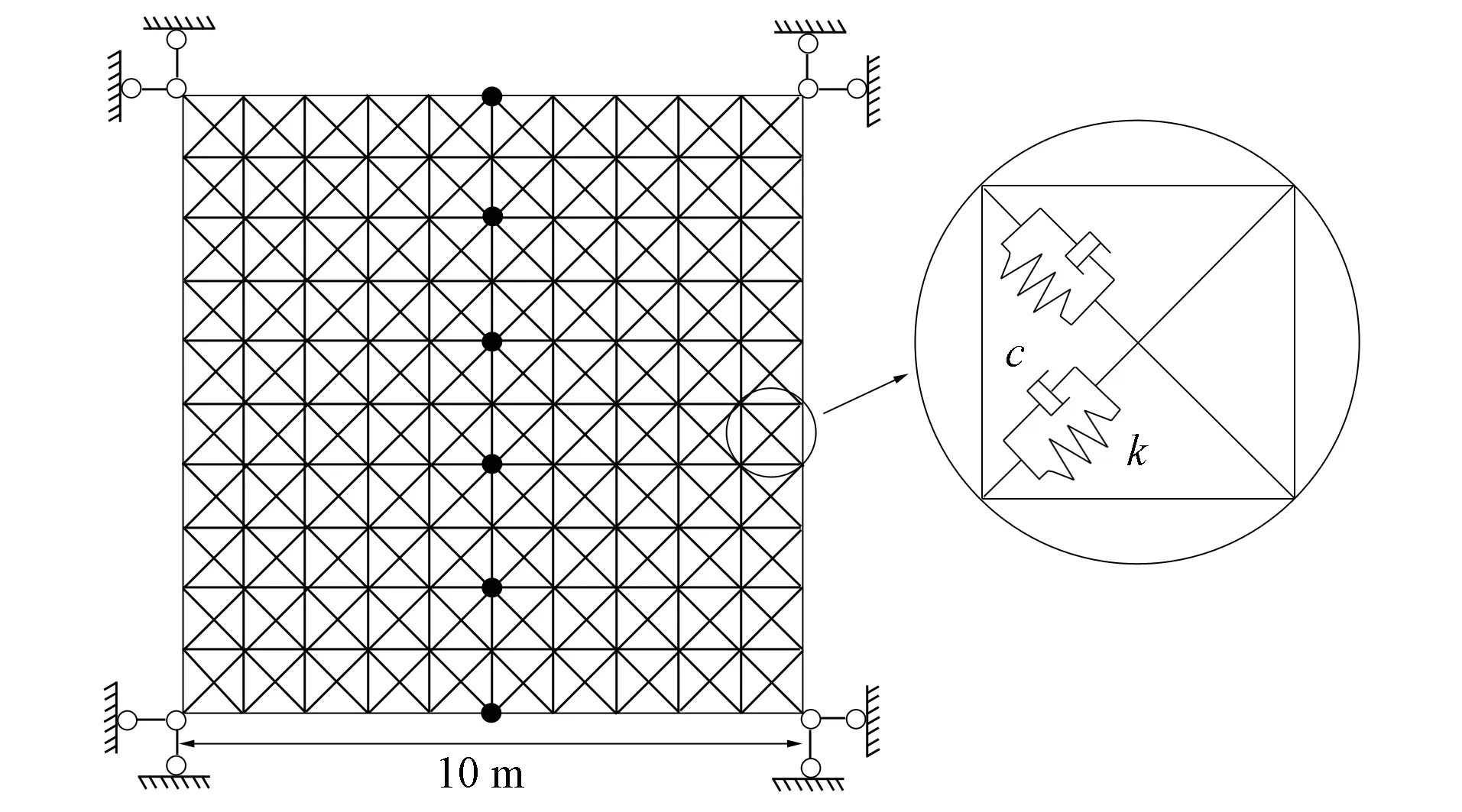
圖2 平面桁架結(jié)構(gòu)Fig.2 Plane truss structure

圖3 桁架結(jié)構(gòu)設(shè)計(jì)變量Fig.3 Design variables of truss structure

表4 平面桁架系統(tǒng)頻率靈敏度比較

表5 平面桁架系統(tǒng)可導(dǎo)模態(tài)振型1及其靈敏度比較

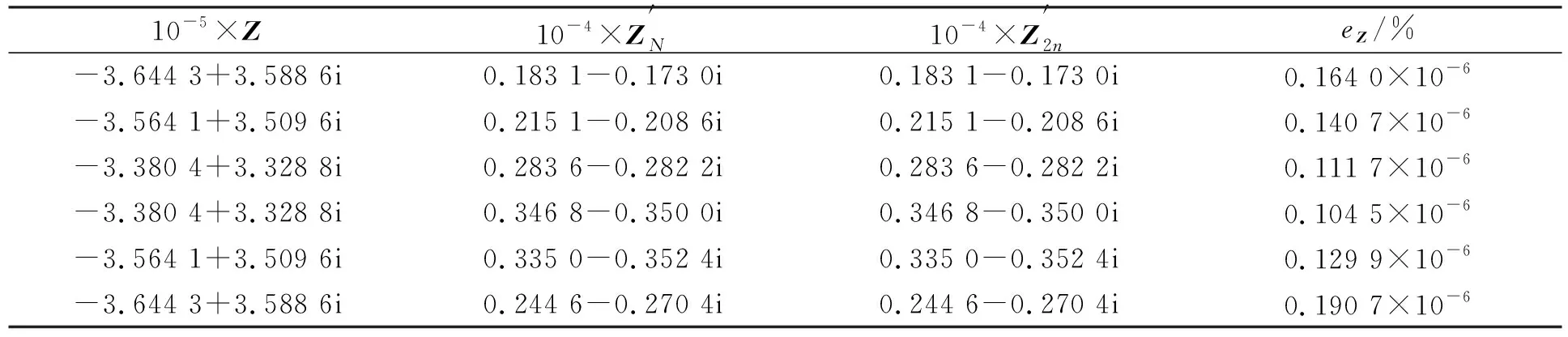
表6 平面桁架系統(tǒng)可導(dǎo)模態(tài)振型2及其靈敏度比較

綜上所述, 針對阻尼結(jié)構(gòu)重頻復(fù)模態(tài)靈敏度計(jì)算問題, 本文提出了一種新的擴(kuò)展Nelson方法, 通過構(gòu)造新的靈敏度特解控制方程, 并證明其系數(shù)矩陣的非奇異性, 使其可以計(jì)算結(jié)構(gòu)重頻復(fù)模態(tài)振型靈敏度. 本文方法僅需利用重頻頻率對應(yīng)的模態(tài)振型, 無需擴(kuò)大方程求解規(guī)模和矩陣重排, 數(shù)值實(shí)例驗(yàn)證了本文方法的有效性.