Hilbert型級數(shù)不等式的研究進展及應用

洪 勇, 陳 強

(1. 廣州華商學院 應用數(shù)學系, 廣州 511300； 2. 廣東第二師范學院 計算機科學系, 廣州 510303)

0 引 言

Hilbert型級數(shù)不等式是研究級數(shù)算子有界性及算子范數(shù)的重要工具, 自1908年Hilbert級數(shù)不等式誕生以來, 隨著獨立參數(shù)的引入和權函數(shù)研究方法的創(chuàng)立, 目前已形成了較完善的理論體系. 1908年, 文獻[1]給出了著名的Hilbert不等式：

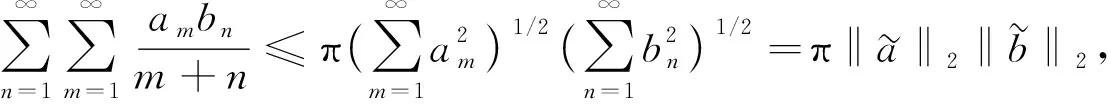
(1)

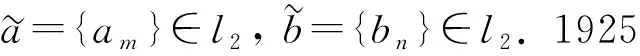
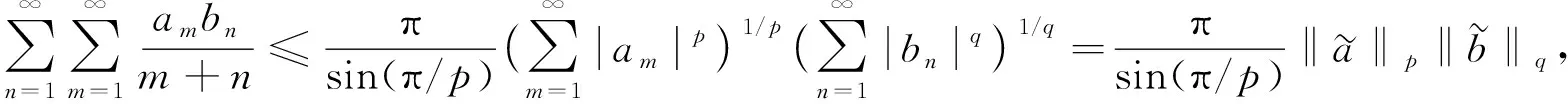
(2)

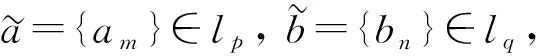
若將序列空間lp推廣為更廣泛的加權序列空間：

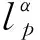
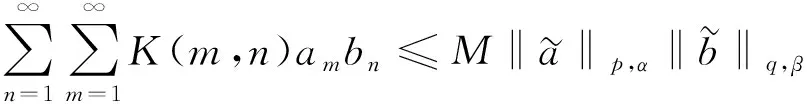
(3)

為Hilbert型級數(shù)不等式.若定義級數(shù)算子T：

則可證明式(3)等價于算子T的不等式：

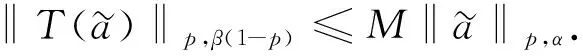
(4)

關于Hilbert型不等式理論和應用的研究目前已取得了豐富成果[3-25]. 文獻[3]對齊次核的Hilbert型積分不等式的研究進展進行了綜述； 文獻[4]對Hilbert型積分不等式從齊次核到非齊次核的發(fā)展進行了回顧. 事實上, Hilbert型級數(shù)不等式是伴隨積分不等式的發(fā)展而發(fā)展的, 它們有許多共性, 也有一些較大差異, 在一定程度上級數(shù)不等式的討論更具挑戰(zhàn)性. 本文對Hilbert型級數(shù)不等式的研究進展與現(xiàn)狀進行分析綜述， 并給出部分最新研究結果.

1 Hilbert型級數(shù)不等式的研究特點

類似于Hilbert型積分不等式, Hilbert型級數(shù)不等式的研究方法仍主要是權函數(shù)方法： 引入兩個搭配參數(shù)a,b, 根據(jù)級數(shù)形式的H?lder不等式可得

引入權函數(shù)：

此時需要對ω1(b,p,m)和ω2(a,q,n)進行處理, 通常需要將其化為積分后再利用實分析的各種技巧進行估算, 要求K(m,t)t-bp和K(t,n)t-aq關于t在(0,+∞)上單調遞減, 若不滿足該遞減條件, 則要用Euler-Marclaurin求和公式對ω1(b,p,m)和ω2(a,q,n)進行分析處理, 因而討論通常變得很困難.若能得到

則可得

從而得到了Hilbert型級數(shù)不等式.然后再討論式(5)的常數(shù)因子是否為最佳的.

從上述過程可見, 用權函數(shù)方法研究Hilbert型級數(shù)不等式, 其特點之一就是要求K(m,t)t-bp和K(t,n)t-aq在(0,+∞)上單調遞減.否則, 要得到具有最佳常數(shù)因子的不等式難度很大.一般地, 任意選取的搭配參數(shù)a,b, 并不能使利用權函數(shù)方法得到的Hilbert型級數(shù)不等式具有最佳的常數(shù)因子, 從而不能得到相應級數(shù)算子的范數(shù), 因此搭配參數(shù)a,b的選取技巧性較高.

2 針對特定核選取特定最佳搭配參數(shù)

引入與共軛指數(shù)(p,q)相獨立的參數(shù), 是Hilbert型不等式研究的重要轉折點, 這一階段的研究特點是： 針對某個含有獨立參數(shù)的具體核, 技巧性地引入適當?shù)拇钆鋮?shù)a,b, 得到具有最佳常數(shù)因子的Hilbert型不等式.

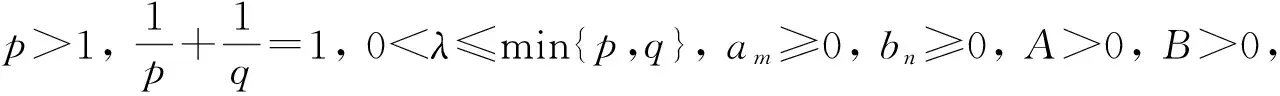
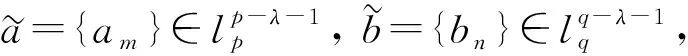
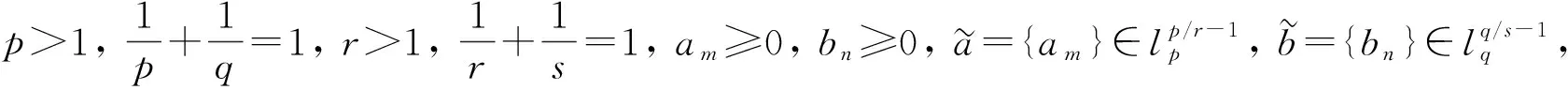
其中常數(shù)因子(r2+s2)是最佳的.

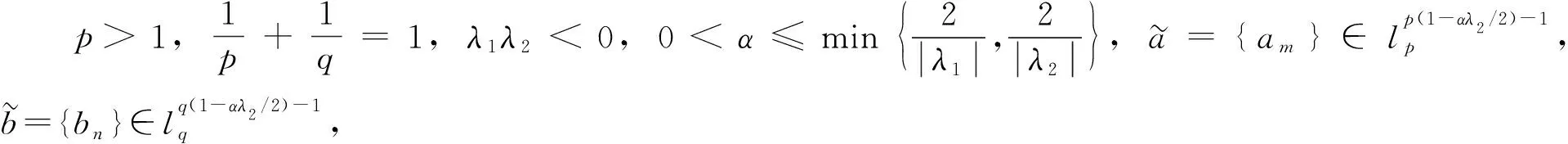
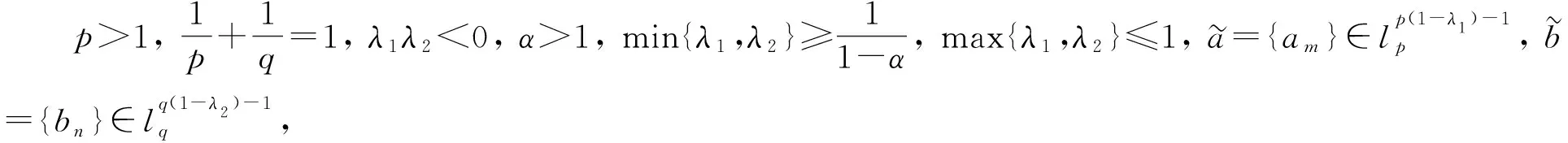
由定理3和定理4可見, 對于同樣的核, 可以選取不同的搭配參數(shù)得到不同的具有最佳常數(shù)因子的Hilbert型不等式.

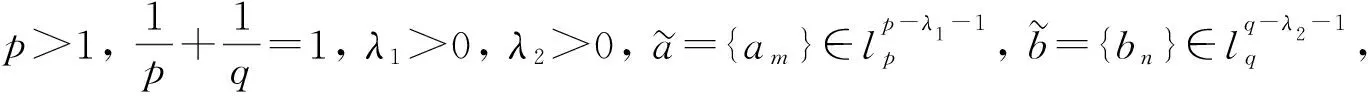
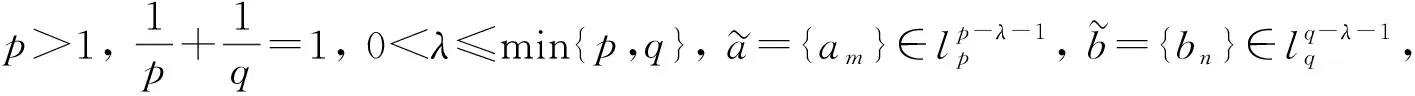
上述具有最佳常數(shù)因子的Hilbert型級數(shù)不等式, 都是基于選取適當?shù)拇钆鋮?shù)a,b后利用權函數(shù)方法得到的.

3 最佳搭配參數(shù)的規(guī)律

要利用權函數(shù)方法獲得最佳Hilbert型不等式, 最核心的問題是要選取最佳的搭配參數(shù)a,b, 因此討論最佳搭配參數(shù)的內在規(guī)律具有重要的理論意義.通過對文獻[6-9]成果的分析研究, 文獻[10]針對擬齊次核的情形, 討論了最佳搭配參數(shù)的充分條件, 但未能證明該條件是否是必要的.文獻[11]針對齊次核的Hilbert型不等式, 得到了完善的結果.

都收斂, 則下列結論成立：

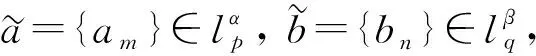
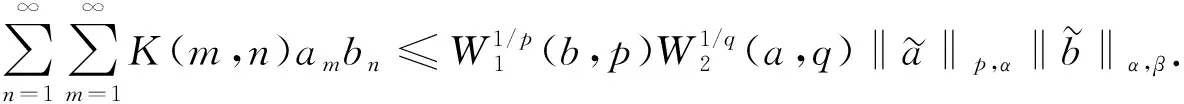
(6)

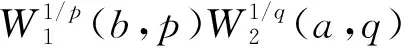
根據(jù)定理7, 可以選取各種滿足bp+aq=λ+2的搭配參數(shù), 利用權函數(shù)方法即可得到很多具有齊次核的最佳Hilbert型級數(shù)不等式.本文通過進一步探討擬齊次核的情形, 可得下列結果.

Gλ(1,tλ2)t-bp,Gλ(tλ1,1)t-aq,Gλ(1,tλ2)t-bp+λ2c/q和Gλ(tλ1,1)t-aq+λ1c/p都在(0,+∞)上遞減, 且

收斂, 則下列結論成立：

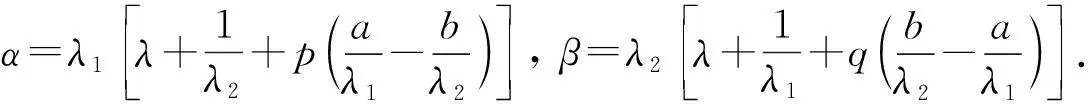
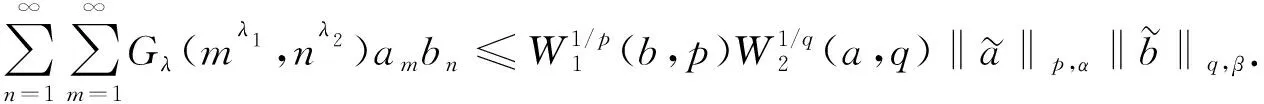
(7)

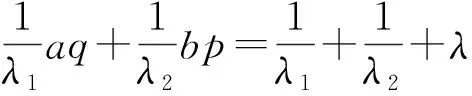
其中W0=|λ2|W1(b,p)=|λ1|W2(a,q).

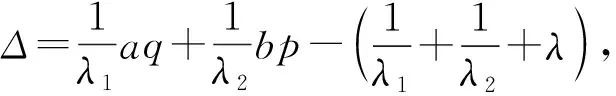
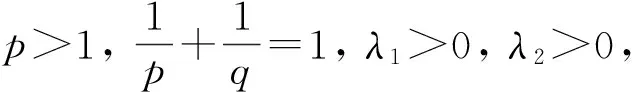
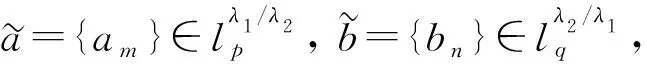
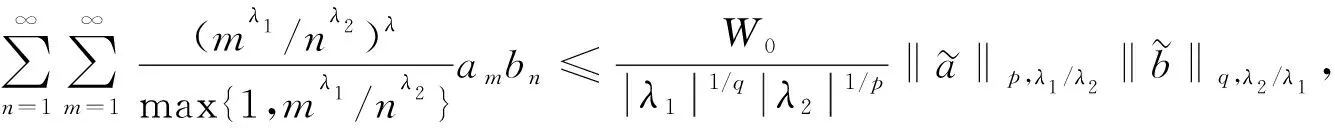
(8)

其中

試判斷不等式的常數(shù)因子是否最佳.

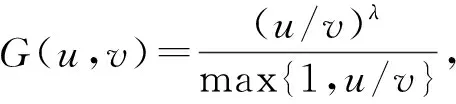
且

故a,b是最佳搭配參數(shù).根據(jù)已知條件, 易知G(1,tλ2)t-bp和G(tλ1,1)t-aq都在(0,+∞)上遞減.因此由定理8知, 式(8)的常數(shù)因子是最佳的.

目前, 關于Hilbert型級數(shù)不等式最佳搭配參數(shù)等價條件的研究已取得了許多成果[12-14].

4 Hilbert型級數(shù)不等式的構建條件

設核Kλ1,λ2,…,λk(m,n)含有參數(shù)λ1,λ2,…,λk, 則Hilbert型不等式

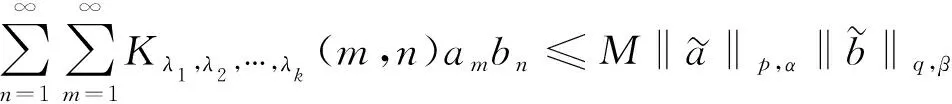
(9)

中含有參數(shù)λ1,λ2,…,λk,p,q,α,β.這些參數(shù)在什么條件下存在常數(shù)M使式(9)成立以及當式(9)成立時, 如何得到其最佳常數(shù)因子, 上述問題是Hilbert型級數(shù)不等式的終極理論問題. 該階段的研究對于最終完善Hilbert型不等式理論意義重大.

文獻[15]首先對Hilbert型不等式的構造進行探討, 開啟了Hilbert型不等式研究的新階段.之后， 我們相繼得到了如下結果.

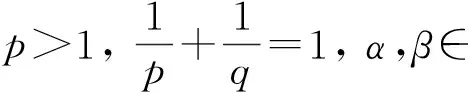
則下列結論成立：

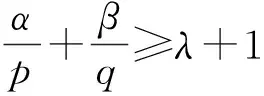
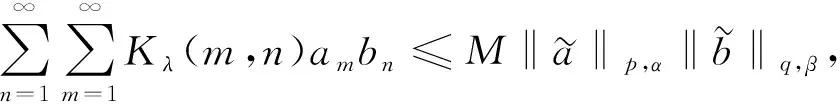
(10)

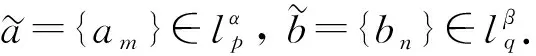
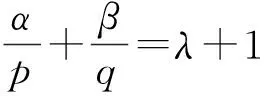
infM=W1(β,q)=W2(α,p).

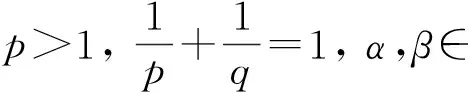
Gλ(1,tλ2)t-(β+1)/q,Gλ(tλ1,1)t-(α+1)/p和Gλ(tλ1,1)t-(α+1)/p+c均在(0,+∞)上遞減, 且

則下列結論成立：

1) 當且僅當c≥0時, 存在常數(shù)M>0, 使得

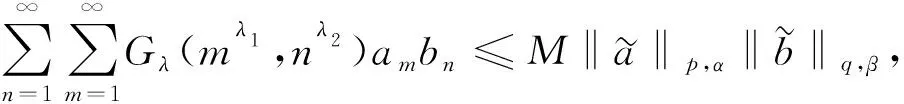
(11)

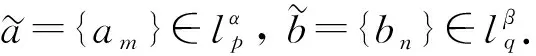
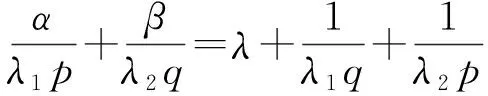
其中W0=|λ1|W2(α,p)=|λ2|W1(β,q).

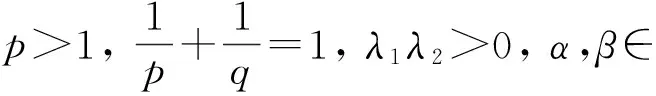
收斂, 則下列結論成立：

1) 當λ1c≥0, 且K(1,t)t-(β+1)/q和K(t,1)t-(α+1-λ1pc)/p均在(0,+∞)上遞減時, 有

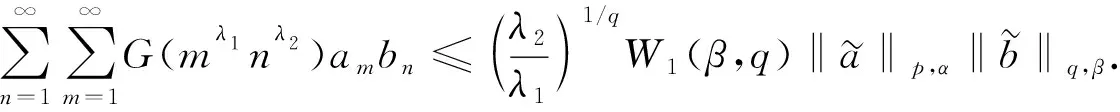
(12)

2) 當λ1c≤0, 且K(1,t)t-(β+1+λ2qc)/q和K(t,1)t-(α+1)/p均在(0,+∞)上遞減時, 有

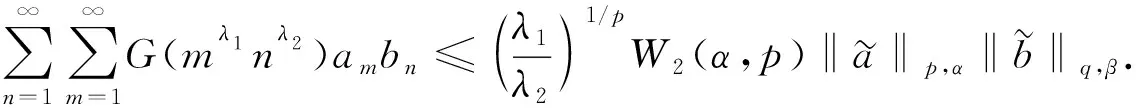
(13)

這里需要指出的是, 式(12)與式(13)的常數(shù)因子并不能確定是否是最佳值, 其最佳常數(shù)因子是什么仍需進一步研究.

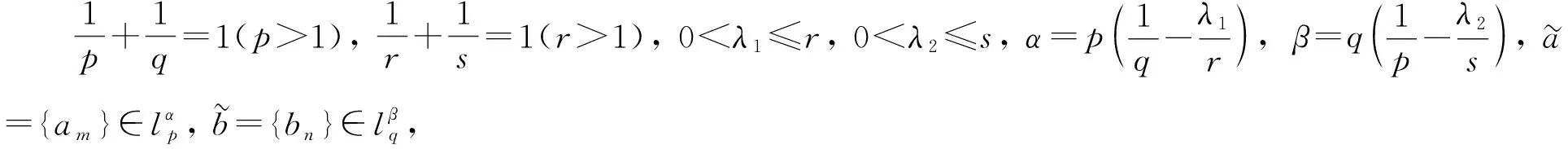
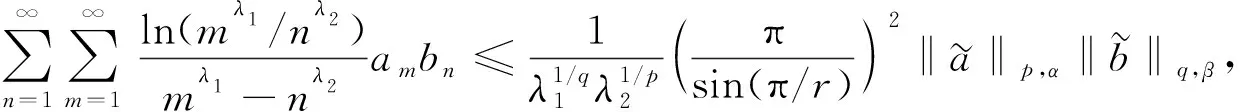
(14)

其中常數(shù)因子是最佳的.

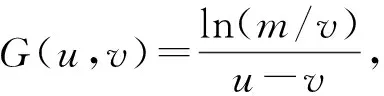
不難驗證

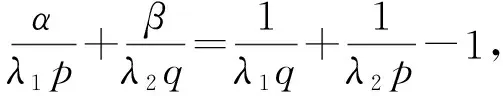
根據(jù)定理10, 式(14)成立, 且其常數(shù)因子是最佳的.

關于Hilbert型不等式構建的其他結果可參見文獻[16-18].

5 重級數(shù)Hilbert型不等式的研究進展

文獻[19]首次對高維Hilbert型不等式進行了探討, 之后涌現(xiàn)了大量高維情形的研究成果, 這些成果有積分型、 級數(shù)型和半離散型, 本文只考慮級數(shù)型Hilbert不等式. 目前, 許多低維Hilbert型級數(shù)不等式的結果都被推廣到了n重級數(shù)的情形, 我們得到了下列結果.

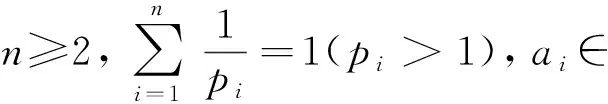
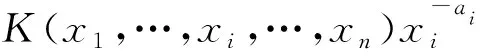
均收斂, 則下列結論成立：

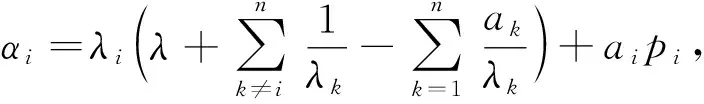
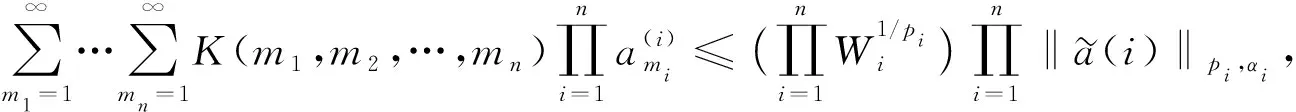
(15)

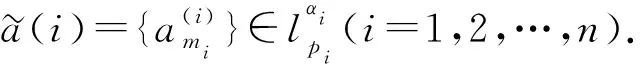
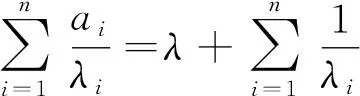
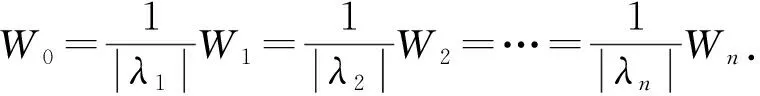
均收斂, 則下列結論成立：

1) 當且僅當c≥0時, 存在常數(shù)M>0, 使得

(16)

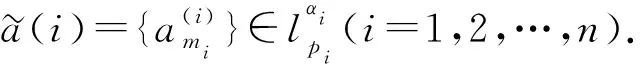
2) 當c=0時, 式(16)的最佳常數(shù)因子為

6 Hilbert型級數(shù)不等式在算子理論中的應用

Hilbert型級數(shù)不等式的重要應用之一, 就是將其用于討論具有相同核的級數(shù)算子的有界性與算子范數(shù). 由于式(3)與式(4)等價, 因而根據(jù)定理10和定理11, 可得下列結果.

定理14在定理10的條件下, 定義級數(shù)算子T為

則下列結論成立：

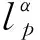
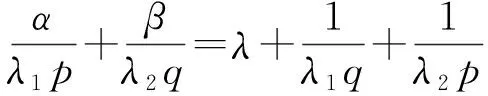
其中W0=|λ1|W2(α,p)=|λ2|W1(β,q).

定理15在定理11的條件下, 定義級數(shù)算子T為

則下列結論成立：

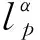
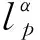
例3試討論級數(shù)算子T：

是否是l2中的有界算子.

解： 記

則G(x3y2)≥0.由于λ1=3,λ2=2,α=β=0,p=q=2, 故

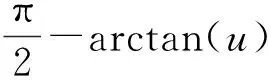
均在(0,+∞)上遞減.又因為

故根據(jù)定理15知,T是l2中的有界算子.