兼具高自由度低互耦的間距約束稀疏陣列設計

岳世杰, 胡國平, 師俊朋, 周 豪, 占成宏

(1.空軍工程大學防空反導學院，西安，710051；2.國防科技大學電子對抗學院，合肥，230000)

陣列信號處理因其優異的波束控制和空間分辨能力而在通信、雷達、聲吶、導航等領域得到廣泛應用[1-5]。由于存在測向模糊，傳統陣列信號處理主要關注陣元間距小于λ/2的均勻線陣(uniform linear array，ULA)，N個陣元的均勻線陣理論上最多可估計N-1個信源[6]，隨著信源數的增多，通常需要增加陣元數來滿足測向需求，這就會相應增加硬件成本和計算復雜度。此外，傳統均勻線陣由于陣元間距較小，陣元間存在較大的互耦，嚴重影響信源估計精度[7]。

稀疏陣列通過向量化協方差矩陣形成差聯合陣列進而擴展孔徑[8]，這為提高自由度、減小陣元間互耦提供了新的思路。早在1968年Moffet就提出了最小冗余陣[9](minimum-redundancy array，MRA)，雖然MRA能夠提供最大連續差聯合陣列，但由于這種陣型結構不存在閉式表達式，隨著陣元數增多，需要大量計算來確定陣元位置，限制了MRA的應用。近年來提出的嵌套陣[10]和互質陣[11]因具有較大的孔徑以及自由度的閉式解而引起學者的廣泛研究。嵌套陣利用N個陣元得到O(N2)個虛擬自由度[10]，極大提高了測量精度和可估計信源數。互質陣陣元間互耦小，但是其差聯合陣列形成的虛擬陣元不連續，因此得到的自由度往往不能充分利用。

在嵌套陣和互質陣的基礎上學者們提出了改進陣列以進一步擴大孔徑，減少互耦。文獻[12]提出了陣元間距壓縮互質陣(co-prime array with compressed inter-element spacing, CACIS)和子陣級聯互質陣(co-prime array with displaced subarrays, CADiS)，CACIS壓縮互質陣中一段子陣的陣元間距，雖然能夠得到更大的連續虛擬陣列，但是CACIS中的最小間距元素間仍存在較大互耦，為克服互耦進而提出了CADiS，將一個子陣移到另一段陣列中，雖能減少互耦，但是其連續虛擬陣元要小于CACIS。文獻[13]提出了將傳統互質陣中一段均勻線陣的陣元數提升一倍的改進型互質陣，進一步提升了差聯合陣列的自由度。文獻[14]提出了改進嵌套陣(improved nested array)將傳統嵌套陣的密集陣元的第1個陣元放到稀疏陣元之后，提升了嵌套陣的自由度，但是陣元間有著嚴重的互耦。文獻[15]提出了二階超級嵌套陣(second-order super nested arrays)，將嵌套陣的密集分布陣元放置在間距較大的陣元之間，在確保自由度的同時，減少了互耦。文獻[16]在此基礎上提出了Q階超級嵌套陣(qth-order super nested arrays)進一步減少了陣元間的互耦。文獻[17]將傳統嵌套陣密集子陣分為4個部分，將其放置到均勻線陣的兩側，提出了增強嵌套陣，根據陣元分集的方式不同，提出了ANAI-1、ANAI-2、ANAII-1和ANAII-2。ANAI-1和ANAI-2雖能提升陣元自由度，但是無法顯著降低陣元間互耦。

針對無法同時優化虛擬陣元孔徑和陣元間互耦的問題，本文提出了一種間距約束稀疏陣列(inter-element spacing restriction array，ISRA)，該陣列基于約束陣元間距設計進而得到陣元位置，形成了4段以一定間隔首尾相連的均勻線陣。ISRA有自由度閉式表達式，且同時做到了自由度與互耦的同步優化，與相同陣元數的互質陣、嵌套陣、二階超級嵌套陣等稀疏陣列相比，使用該陣列進行DOA估計效果更好，最后通過計算仿真驗證了使用ISRA估計的有效性。

1 稀疏陣列回波信號模型

設有K個窄帶遠場不相干信號入射到由N個陣元構成的非均勻線陣，陣元位置分布在nid，其中ni∈Z，且S={ni,i=1,2,…,N}，d=λ/2，其中λ為信號波長。設K個信源入射角度為θ={θk,k=1,2,…,K}，則陣列回波信號模型為：

x(t)=As(t)+N(t)

(1)

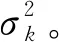
由x(t)可計算回波協方差矩陣為：

(2)

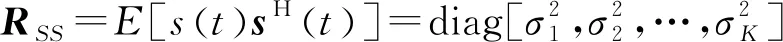
對回波信號協方差矩陣RXX向量化可得：

(3)

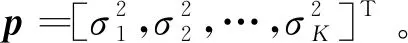
由A*°A得到稀疏陣列虛擬陣元位置是實際陣元位置的差聯合陣列[18]。

2 間距約束稀疏陣列結構設計

二階超級嵌套陣是在嵌套陣的基礎上將密布的子陣分解為六段盡可能稀疏的子陣，進而減少陣元間的互耦。ISRA設計借鑒二階超級嵌套陣的設計思想，將陣列分為4段盡可能稀疏的子陣，并加入間距約束的思想，即除必須的一對陣元間距為d外，約束其他所有的陣元間距至少為2d并盡可能增大間距大于2d的陣元的數量。

如圖1所示，給出ISRA結構，基于給定陣元數S，限制物理陣元之間的間距，進而確定物理陣元的位置。總陣元數為S=N1+N2+1，N1≥4且N1為偶數，N2∈Z+。該陣列由X1,X2,X3,X4這4段均勻線陣拼接而成。為減少陣元間互耦，則至少需要陣元間距為2d，因此約束兩段均勻線陣的間距為2d，即陣元間距為2d，陣元數目為N1/2-1的均勻線陣構成的第一部分X1和陣元間距為2d，陣元數為N1/2-2的均勻線陣構成的第2部分X2；為進一步擴展陣列孔徑，約束一段間距較大的均勻線陣，即由陣元間距為N1d，陣元數為N2的均勻線陣組成第3部分X3，N2≥1；為形成密布虛擬陣元，則至少需要有一段陣元間距為d，因此約束第四部分由陣元間距為d的2個陣元構成。約束X1,X2,X3,X4這4段均勻線陣之間的間距大于2d并通過調試得到這4段均勻線陣之間的間距分別為3d,N1d,(N1-3)d。通過約束各段均勻線陣陣元間距以及各段線陣之間的間距組成的ISRA能夠形成連續的密布虛擬陣。

圖1 ISRA陣元結構配置

令A表示為相鄰陣元間距的集合，即A中第k個元素為第k個物理陣元和第k+1個物理陣元之間的間距。式(10)給出了陣元間距設置。假設參考陣元位于坐標軸0處，由相鄰陣元間距確定陣元位置S。

(4)

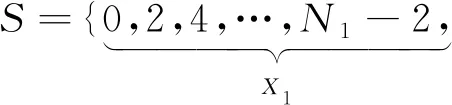
(5)

ISRA陣元位置是由N1，N2共同決定的，且總陣元數S=N1+N2+1，當給出S、N1、N2任意2個變量的值都能唯一確定集合A的值，進而確定陣元位置S。

3 間距約束稀疏陣列自由度

定理：ISRA的差聯合陣列是密布均勻線性陣列，且該陣列的自由度為：

(6)

證明：

令X+={0,1,2,…,(N2+3)N1-6,(N2+3)N1-5}，為集合X中大于等于0的部分，令D+為差聯合陣列D中大于等于0的部分，D代表ISRA陣元位置S的差聯合陣列。則只需要證明ISRA的差聯合陣列D=X。由權重函數[15]知X、D中元素關于0對稱分布，則只需要證明D+=X+。

將差聯合陣列的正向部分X+分為4個子集，分別為φ1={0,1,2,…,N1-1}、

φ2={N1,N1+1,N1+2,…,N1(N2+1)-2}、

φ3={N1(N2+1)-1,N1(N2+1),…,N1(N2+2)-5}

φ4={N1(N2+2)-4,N1(N2+2)-3,…N1(N2+3)-5}

定義集合和數字加減運算：

A±c={a±c|?a∈A}

(7)

定義集合和集合的運算：

diff(A,B)={a-b|?a∈A,?b∈B,a>b}

(8)

設：

(9)

情形1：證明φ1?D+

顯然{0,1}?D+

(10)

因為{N1-2,X1,N1+1}?S，則：

P1=

diff(N1-2,X1)={0,2,4,…,N1-2}?D+

(11)

P2=

diff(N1+1,X1)={3,5,7,…,N1+1}?D+

(12)

P1∪P2=

{0,2,3,4,…,N1-2,N1-1,N1+1}?D+

(13)

由式(10)～(13)得：φ1?D+。

情形2：證明φ2?D+

由{X1,X2,X3,2N1-3,(3+N2)N1-5}?S，

X3∪{2N1-3}={(2N1-3)+qN1|0≤q≤N2,q∈Z+}?D+，

P3=diff(X3∪{2N1-3},X1)=

diff(2N1-3,X1)+qN1=

{N1-1,N1+1,N1+3,…,2N1-3}+qN1?

{N1-1,N1+1,N1+3,…,2N1-3}+mN1

(14)

P4=diff(X3∪{2N1-3},X2)=

{0,2,4,…,N1-4}+qN1?

{N1,N1+2,N1+4,…,2N1-4}+mN1

(15)

P5=diff((3+N2)N1-5,{2N1-3}∪X3)=

diff((1+N2)N1-2,qN1)=

{N1-2,2N1-2,3N1-2,…,(1+N2)N1-2}?

{2N1-2}+mN1

(16)

其中：

0≤q≤N2,q∈Z+；0≤m≤N2-1,m∈Z+。

得P3?D+，P4?D+，P5?D+，P3∪P4∪P5?D+

又φ2?P3∪P4∪P5，則φ2?D+

同理可得φ3?D+,φ4=?D+。

綜上可得：

X+=φ1∪φ2∪φ3∪φ4?D+

(17)

且max (D+)=max (S)-min (S)=(N2+3)N1-5，min (D+)=0。則：

D+?{0,1,2,…,(N2+3)N1-5}=X+

(18)

由式(17)、(18)得D+=X+。

證畢。

由定理知，ISRA的自由度是由N1和N2共同決定的，下面引理給出如何確定N1和N2的值才能獲得最大的自由度。

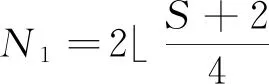
證明：

由定理知ISRA虛擬陣列滿足X，且X中元素遍歷所有在min (X)和max (X)之間的整數，則虛擬陣列自由度為DOF=max (X)-min (X)+1

設N1=2k，k∈Z+

DOF=2(N1(N2+3)-5)+1=

-8k2+4(S+2)k-9

(31)

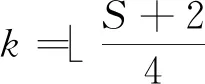
表1給出了在已知陣元總數S的情況下ISRA的差聯合陣列自由度。由表可以看出ISRA利用4r個陣元可以實現O(8r2)數量級的虛擬陣列自由度。

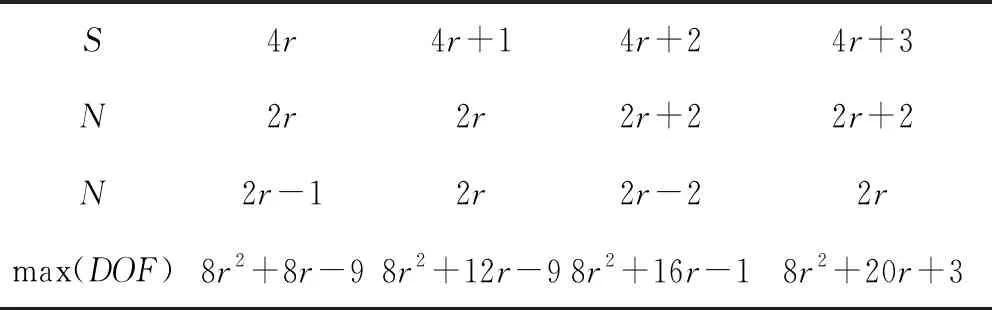
表1 ISRA配置

4 仿真實驗

本節將通過仿真驗證ISRA在減少互耦以及提高DOA估計精度方面的優勢。仿真實驗的計算機平臺為Intel(R)Core(TM)i7-9750H CPU @ 2.60 GHz 2.59 GHz, RAM 8.00 GB，軟件為Matlab(R2020a)。首先對比各稀疏陣列權重以及互耦率[15]，隨后對比無互耦條件下DOA估計的均方值誤差，最后分析陣元間存在耦合條件下不同陣列DOA估計的均方值誤差。對于稀疏陣列，采用MUSIC算法[21]進行DOA估計。假設所有信源的功率相當且信源數一定，為了定量評價DOA估計結果，將歸一化DOA估計均方根誤差(共進行500次蒙特卡羅仿真實驗)定義為：

(20)

4.1 權重及互耦矩陣

比較不同稀疏陣列與ISRA在陣列設計上的性能，表2給出了在不同陣元數情況下五種稀疏陣列的權重及互耦率。在表2給出的10陣元、15陣元、20陣元的情況下，嵌套陣和增強嵌套陣的權重ω(1)較大，而互質陣、二階超級嵌套陣和ISRA保持著較低的ω(1)，且ISRA的權重ω(1)始終保持最低，為1，這反映了ISRA在這5種陣列中始終保持著較低數量的密布陣元。互質陣、二階超級嵌套陣以及ISRA都保持著較低的互耦率，而嵌套陣和增強嵌套陣由于密布陣元較多而有著較高的互耦率。二階超級嵌套陣和相同陣元數的嵌套陣擁有相同的虛擬孔徑，但其互耦率要低于嵌套陣，這其中一部分原因是二階超級嵌套陣在嵌套陣的基礎上將密布子陣放置到稀疏的位置。ISRA的互耦率低于二階超級嵌套陣，一方面是因為相同陣元數的ISRA自由度要大于二階超級嵌套陣，另一方面ISRA通過間距約束使得權重ω(1)=1，減少了密布陣元的數量。

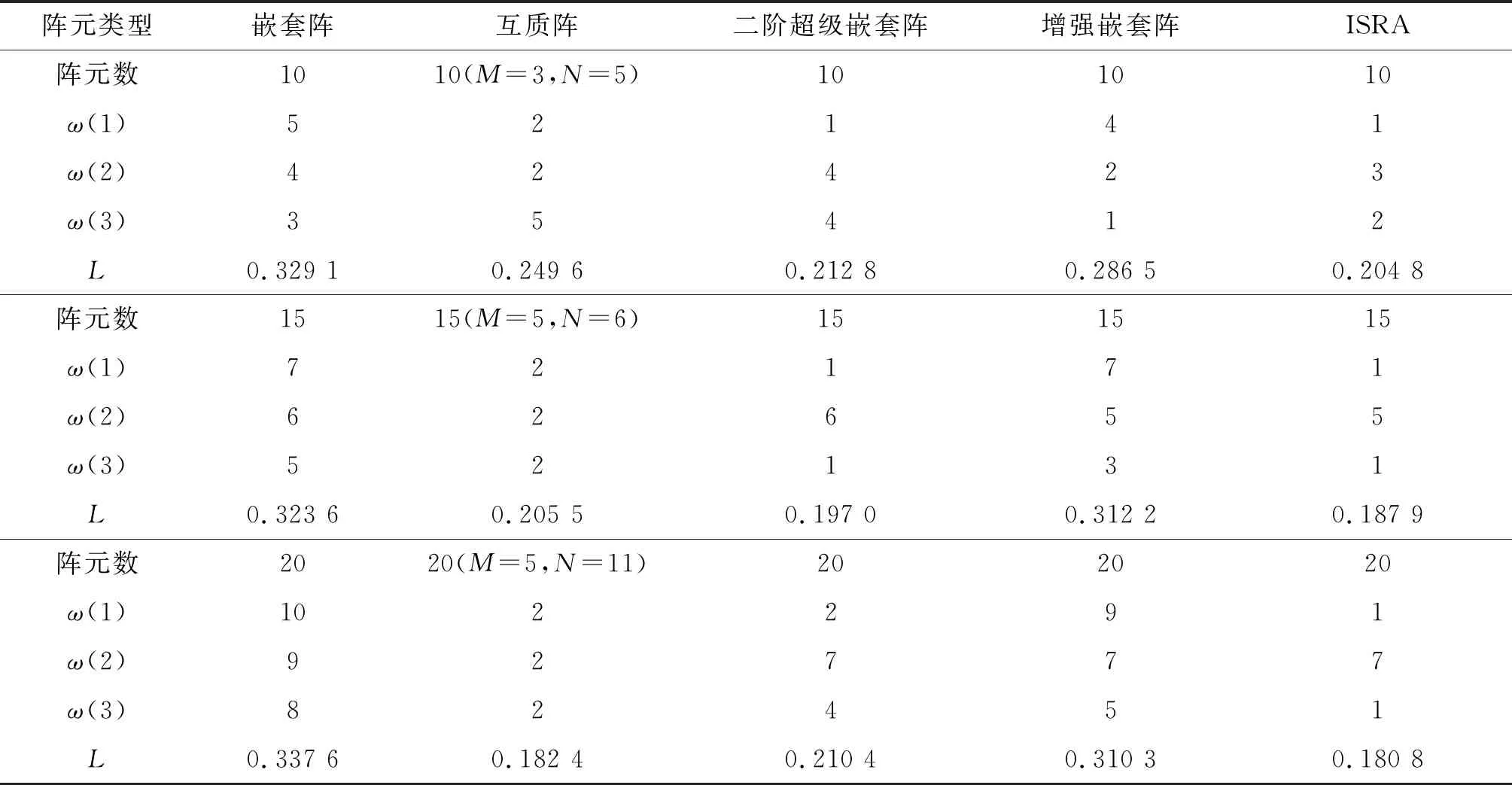
表2 5種稀疏陣列權重及互耦率對比

4.2 不考慮陣元耦合DOA估計

本節比較在無互耦的情況下，最小冗余陣、嵌套陣、互質陣、二階超級嵌套陣、增強嵌套陣以及ISRA的DOA估計性能。設定陣元數為14，最小冗余陣陣元位置設定為[20]：

SMRA=

{0, 1, 2, 8, 15, 16, 26, 36, 46, 56, 59, 63, 65, 68}

(33)

對于嵌套陣以及二階超級嵌套陣，設定N1=N2=7，互質陣按照文獻[13]設定為M=4,N=7。

4.2.1 MUSIC空間譜

圖2給出了不同稀疏陣列的MUSIC算法的空間譜，設共有50個信源均勻分布在[-80°,80°]，第k個信源的角度為：θk=-80°+160°(k-1)/49，其中1≤k≤50。設定信噪比為0 dB,快拍數為1 000。可以看出由于互質陣列的差聯合陣列密布的陣元數目較少，不能有效分辨出50個信源。其余陣列均能有效分辨出50個信源，且可觀察到最小冗余陣、增強嵌套陣以及ISRA的譜峰明顯高于嵌套陣以及二階超級嵌套的譜峰，這反映了最小冗余陣、增強嵌套陣以及ISRA在孔徑上的優勢使得角度估計的精度更高。

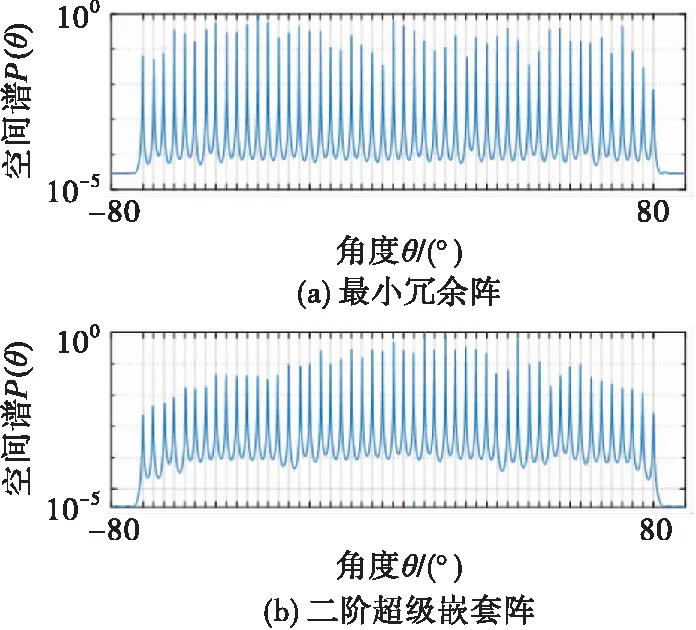
圖2 不同陣列無互耦空間譜估計譜峰圖

4.2.2 均方根誤差

假設3個信源分布在-5°、0°、5°的位置。圖3給出了均方根誤差隨信噪比增大的變化曲線，設定快拍數為1 000，信噪比從-30 dB以5 dB的步長增加到30 dB。從橫坐標來看：信噪比小于-20 dB時所有陣列的均方根誤差均較大，隨著信噪比的增大均方根誤差減小且最小冗余陣減小的速度最大，當信噪比大于10 dB時均方根誤差趨于穩定。從縱坐標來看，當均方根誤差趨于穩定時最小冗余陣均方根誤差最小，互質陣的均方根誤差最大，這是因為最小冗余陣有最大數目的連續虛擬陣元，而互質陣連續的虛擬陣元數目最小。ISRA和增強嵌套陣的估計效果略好于嵌套陣和二階超級嵌套陣。

圖3 歸一化均方根誤差隨信噪比變化曲線

圖4給出了均方根誤差隨快拍數的變化曲線，設定信噪比為0 dB，快拍數從10以300為步長增加到3 010。從橫坐標來看，當快拍數小于310時所有陣列的均方根誤差較大。隨著快拍數的增大，均方根誤差減小，在快拍數小于310時均方根誤差減小的趨勢最大，之后均方根誤差減小的趨勢減緩。從縱坐標來看，均方根誤差趨于穩定后，最小冗余陣有著最小均方根誤差，互質陣的均方根誤差最大。ISRA和增強嵌套陣均方根誤差相差較小，且略大于嵌套陣和二階超級嵌套陣，這是由于ISRA和增強嵌套陣擁有相同大小的連續虛擬陣元，且ISRA和增強嵌套陣的虛擬陣元數目大于嵌套陣和二階嵌套陣的虛擬陣元的數目。

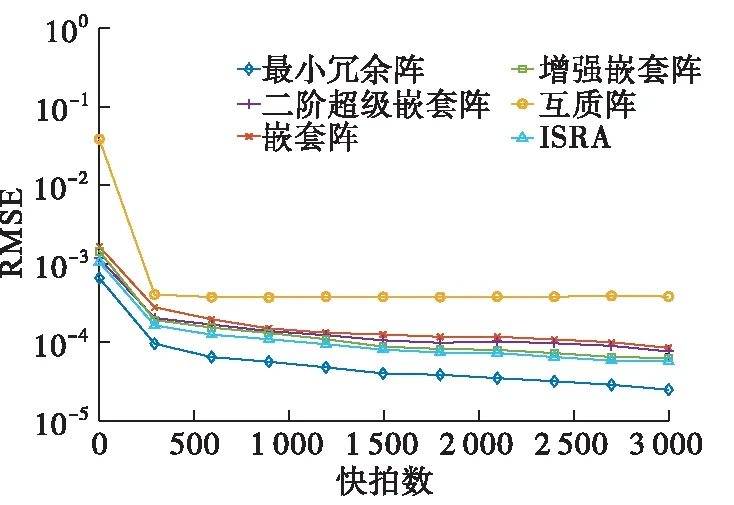
圖4 歸一化均方根誤差隨快拍數變化曲線

4.3 考慮陣元耦合DOA估計

本節考慮互耦對信源角度估計的影響，對比最小冗余陣、嵌套陣、互質陣、二階超級嵌套陣、增強嵌套陣、ISRA的DOA估計性能。設定陣元數為14，陣元位置分布同4.2節。

4.3.1 MUSIC空間譜

設共有30個信源θk=-80°+160°(k-1)/29，其中1≤k≤30，信噪比為0 dB，快拍數為1 000，圖5給出了有互耦影響下不同陣列譜峰圖。可以看出所有陣列的空間譜的譜峰由于互耦影響都出現不同程度的削弱，但是ISRA仍能有效檢測到30個信源；最小冗余陣、嵌套陣以及增強嵌套陣由于互耦在一個角度區間內出現多個譜峰；其余陣列則缺失譜峰或者譜峰偏離真實信源角度過遠。

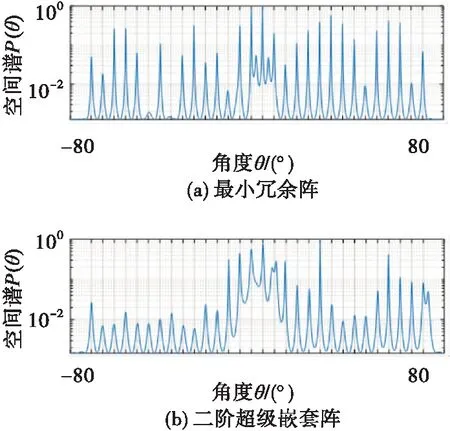
圖5 不同陣列互耦影響下空間譜估計譜峰圖

4.3.2 均方根誤差

假設3個信源分布在-5°、0°、5°的位置。設定快拍數為1 000，信噪比從-30 dB以5 dB的步長增加到30 dB。圖6給出了歸一化均方根誤差隨信噪比變化曲線。從橫坐標來看，當信噪比小于-20 dB時，陣列的均方根誤差較大，隨著信噪比的增大均方根誤差減小，并在大于0 dB之后趨于穩定。均方根誤差隨信噪比減緩的速度在小于-20 dB時最大。從縱坐標來看，當均方根誤差趨于穩定后嵌套陣的均方根誤差最大，這是密集子陣互耦帶來的影響。ISRA均方根誤差最小，與最小冗余陣相比，雖然ISRA的自由度要小于最小冗余陣，但是ISRA受互耦影響更小，這就使得ISRA的估計效果要好于最小冗余陣。

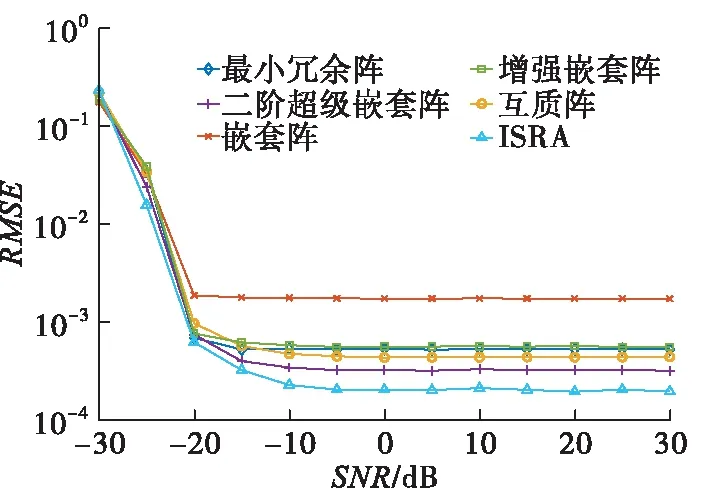
圖6 歸一化均方根誤差隨信噪比變化曲線

圖7給出了均方根誤差隨快拍數的變化曲線，設定信噪比為0 dB，快拍數從10以300為步長增加到3 010。從橫坐標來看，在快拍數較小時，陣列的均方根誤差較大，隨著快拍數的增大均方根誤差趨于穩定。從縱坐標來看，均方根誤差趨于穩定后，ISRA的均方根誤差最小，嵌套陣的均方根誤差最大。其余陣列的均方根誤差由小到大依次是二階超級嵌套陣、互質陣、最小冗余陣和增強嵌套陣。可得最小冗余陣和增強嵌套陣雖然有著大的連續虛擬陣元數目，但是互耦的影響使得他們的估計效果仍不理想。

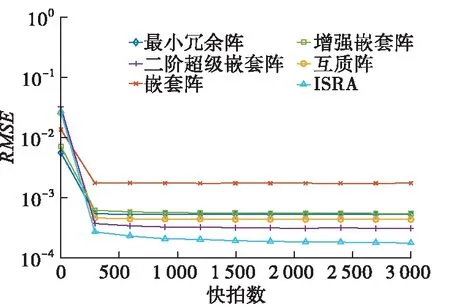
圖7 歸一化均方根誤差隨快拍數變化

5 結語

本文設計了一種兼具高自由度與低互耦率的間距約束稀疏陣列，該陣列給定陣元數量后即可唯一確定陣元分布位置以及差聯合陣列的自由度。理論分析表明，該陣列的差聯合陣列是無孔陣列，與嵌套陣、超級嵌套陣相比擁有更大的自由度；與互質陣、最小冗余陣和增強嵌套陣相比擁有更小的互耦。最后通過仿真驗證了該新型陣列在測向方面的優越性。