無K3子圖的圖中1-因子計數
楊 利 民,年 四 洪
(1.大理大學 數學與計算機學院,云南 大理 671003;2.大連理工大學 數學科學學院,遼寧 大連 116024)
0 引 言
1-因子或完美匹配在量子化學、晶體物理學和計算機領域中有重要應用.1-因子或完美匹配是覆蓋圖的所有頂點的不交邊的集合.Tutte在1947年給出1-因子或完美匹配存在的一個充分必要條件[1].這個結果是圖論中的奠基性的定理,在圖論歷史上有重要意義,然而如何判斷1-因子或完美匹配的存在,仍是一個十分困難的問題.相比之下,計算1-因子的個數是更困難的.S(n)-因子計數理論包括S(n)-因子的表示公式和分支分析方法.通過利用已建立的S(n)-因子計數理論和組合數學方法,可以解決無K3子圖的圖中1-因子計數.
1 定義和引理
定義1令S(n)={Ki:1≤i≤n},n≥1,并且Ki是有i個頂點的完全圖,如果M是圖G的一個子圖,且M的任意分支都同構于S(n)={Ki:1≤i≤n}的某一元素,那么M叫作圖G的一個S(n)-子圖,如果M是圖G的一個生成子圖,那么M叫作圖G的一個S(n)-因子.
恰有k個分支的S(n)-因子的個數記為N(G,k).
S(n)-因子計數的表示公式如下.
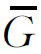
圖論中分支分析方法公式如下:
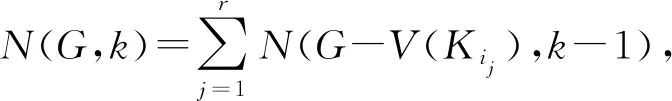
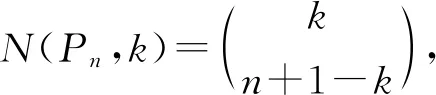
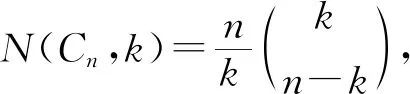
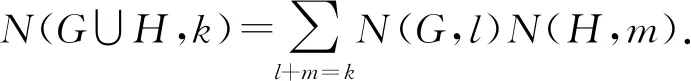
2 主要結果
用f(G)記圖G中1-因子的個數.
定理1如果圖G是無K3子圖或三角形的任意圖,那么f(G)=N(G,n/2).
證明因為圖G是無K3子圖或三角形的任意圖,所以它就沒有K4,K5,…,Kn子圖,從而S(n)-因子的元素只能是K1或K2,即每一個元素是頂點或邊.N(G,n/2)是恰有n/2個分支的S(n)-因子的個數,N(G,n/2)的每一分支都是K2,即邊,而1-因子是覆蓋圖G的不交邊的集合,所以有公式f(G)=N(G,n/2).
□
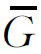
其中S(p,n/2)是第二類Stirling數.
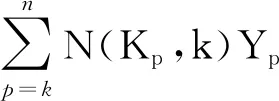
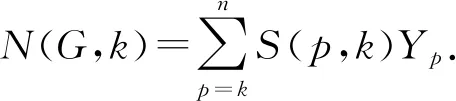
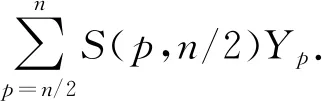
因為圖G是無K3子圖或三角形,根據定理1,得到f(G)=N(G,n/2),所以無K3子圖的圖G中1-因子的計數公式為
□
例1假設圖G是一個完全2-部圖Kn,n,那么
其中s(n,k)是第一類Stirling數,S(p,k)是第二類Stirling數.
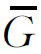
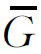
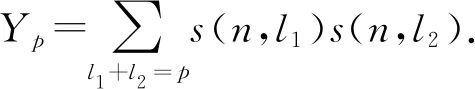
通過定理2,得到完全2-部圖Kn,n的1-因子的計數公式
□
推論1對于兩類Stirling數有組合恒等式:
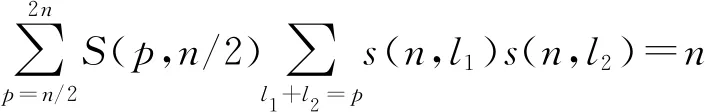
證明通過組合計數得到在完全2-部圖Kn,n中1-因子的個數f(G)=n!.
根據例1,完全2-部圖Kn,n的1-因子的計數公式
所以對于兩類Stirling數有組合恒等式:
□
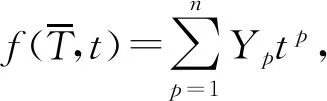
證明如果T是一棵樹,那么T是無K3子圖或三角形.通過定理2,得到樹的1-因子的計數公式為
□
推論2對于兩類Stirling數有組合恒等式:
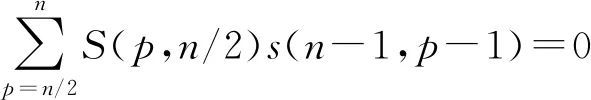
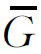
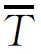
其中Yp=s(n-1,p-1),根據例2,得到
另一方面,在K1,n-1中1-因子的個數f(K1,n-1)=0.
綜上所述,對于兩類Stirling數有組合恒等式:
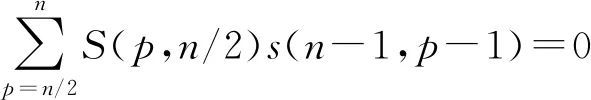
□
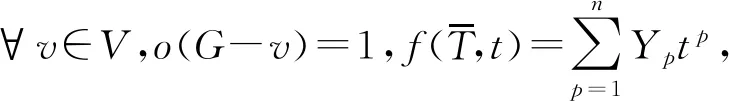
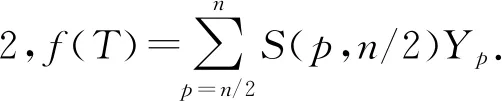
因為圖G是一棵樹,且對?v∈V,o(G-v)=1,于是在圖G中存在1-因子[1],得到f(G)≥1.

□
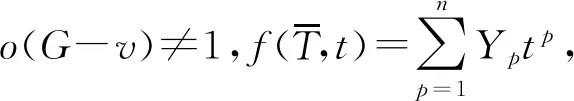
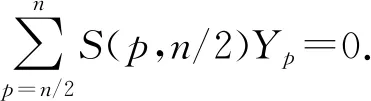
□
以下闡述圖的分支分析方法計算無K3子圖的1-因子的計數.
定理3如果圖G是有n個頂點的圖,且為無K3子圖,P是圖G的一個固定頂點,通過頂點P的所有完全圖是Ki1,Ki2,…,Kir,那么圖G中的1-因子的計數公式為
其中G-V(Kij)是刪掉頂點V(Kij)和與V(Kij)相關聯的邊所得到的圖.
證明因為圖G是無K3子圖,根據定理1,
f(G)=N(G,n/2)
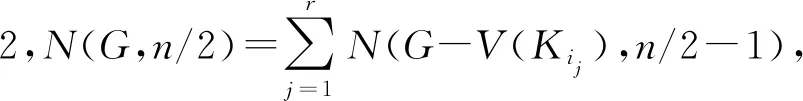
□
定理4假設圖G是無K3子圖,1-因子存在的充分必要條件是N(G,n/2)≥1.
證明略.
復雜性:計算N(G,n/2).
定理5假設圖G是無K3子圖,1-因子不存在的充分必要條件是N(G,n/2)=0.
證明略.
例3假設圖1被構造如下,其中Cn是n個頂點的圈,且n是偶數,圈Cn的個數是q,那么f(G)=2q.
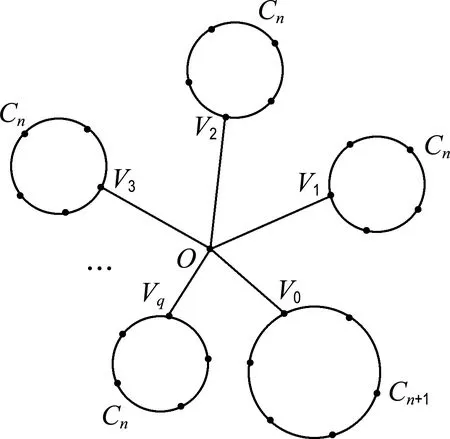
圖1 毽子圖Fig.1 Shuttlecock picture
證明利用分支分析方法,對固定頂點O進行分析,通過頂點O的所有完全圖是O,OV0,OV1,…,OVq,即K1和(q+1)K2.圖1無K3子圖.
情況1O作為K1,刪掉頂點O,于是有q個圈Cn和一個圈Cn+1,它們兩兩不相交,
N(G-V(K1),k-1)=N(Cn+1∪Cn∪…∪Cn,k-1)
情況2過O點的完全圖為OV0,刪掉OV0,于是有q個圈Cn和一個路Pn-1,它們兩兩不相交,
N(G-V(K1),k-1)=N(Pn-1∪Cn∪…∪Cn,k-1)
情況3過O點的完全圖為OV1,OV2,…,OVq,刪掉OV1,OV2,…,OVq,因為OV1,OV2,…,OVq是對稱的,于是
N(G-V(OV1),k-1)=
N(G-V(OV2),k-1)=…=
N(G-V(OVq),k-1)=
N(Cn+1∪Pn-2∪Cn∪…∪Cn,k-1),
N(G-V(OV1),k-1)+N(G-V(OV2),k-1)+
…+N(G-V(OVq),k-1)=
qN(Cn+1∪Pn-2∪Cn∪…∪Cn,k-1)
利用引理2和5,有
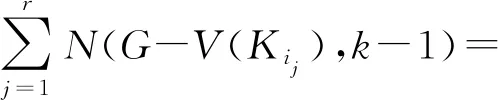
N(G-V(K1),k-1)+
N(G-V(OV0),k-1)+
N(G-V(OV1),k-1)+
N(G-V(OV2),k-1)+…+
N(G-V(OVq),k-1)=
N(Cn+1∪Cn∪…∪Cn,k-1)+
N(Pn-1∪Cn∪…∪Cn,k-1)+
qN(Cn+1∪Pn-2∪Cn∪…∪Cn,k-1)=
N(Cn,l3)…N(Cn,lq+1))
圖1中頂點的個數是(q+1)n+2.根據定理3、引理3和引理4[5-6],
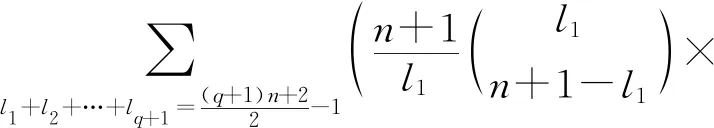
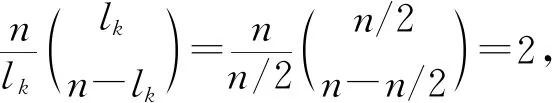
f(G)=0+2q+q×0=2q.
圖1中存在1-因子,且為2q個.
□
例4假設圖2被構造如下,其中Pn是長度為n且有n+1個頂點,Pn的個數是q,那么f(G)=0.
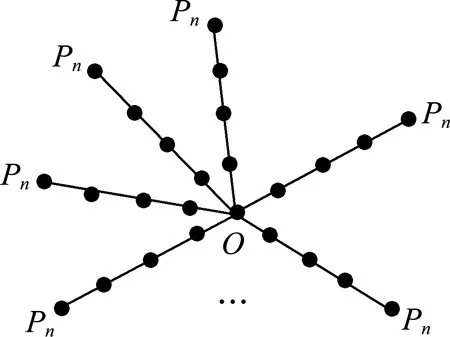
圖2 棒圖Fig.2 Bar graph
證明類比于例3,利用圖的分支分析方法,對固定點O進行分析.通過頂點O的所有完全圖是K1和q個K2.圖2無K3子圖.
情況1O作為K1,為一個完全分支,刪掉K1,有q個路Pn-1,并且兩兩不相交,于是
N(G-V(K1),k-1)=N(Pn-1∪Pn-1∪…∪
Pn-1,k-1)
情況2O含于K2,作為一個完全分支,刪掉K2,有一個路Pn-2和q-1個路Pn-1,因為q個完全圖K2是對稱的,于是
qN(G-V(K2),k-1)=qN(Pn-2∪Pn-1∪…∪
Pn-1,k-1)
綜上所述,根據引理2和5,得到
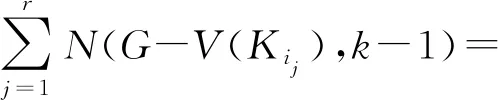
N(G-V(K1),k-1)+
qN(G-V(K2),k-1)=
N(Pn-1∪Pn-1∪…∪Pn-1,k-1)+
qN(Pn-2∪Pn-1∪…∪Pn-1,k-1)=
N(Pn-1,lq)+
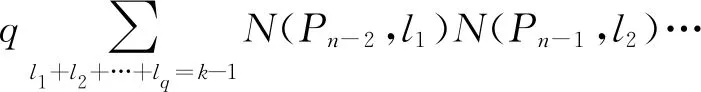
圖2中頂點的個數是qn+1,由于圖2無K3子圖,根據定理3和引理3,有
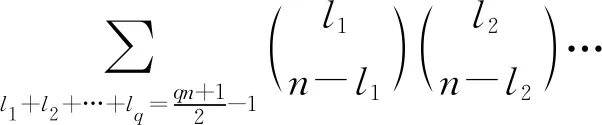
當q或n是偶數時,qn+1是奇數,在圖2中,f(G)=0.
當q和n都是奇數時,qn+1是偶數,在圖2中,f(G)=0+q×0=0[7].
在圖2中,對任意q和n,不存在1-因子.
□
注構造這兩類圖,1-因子可能無限或為零.
定理6對任意自然數N,存在連通圖使得它的1-因子個數大于自然數N.
證明構造一個圖,如例3的圖1,根據例3的結果,該圖的1-因子個數f(G)=2q.
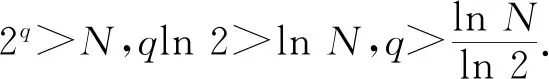

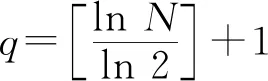
□
3 結 語
1-因子或完美匹配的計數是十分困難和有價值的問題.本文利用S(n)-因子計數理論和組合數學方法研究了無K3子圖的圖中的1-因子計數,取得了一定的進展,對于組合學和圖論具有一定參考價值.

