基于區間算法的直流輸電系統元件可靠性參數求解模型

李凌飛，侯婷，李巖，姬煜軻，黃瑩，辛清明，傅闖，李歡

(直流輸電技術國家重點實驗室(南方電網科學研究院)，廣州 510663)

0 引言

高壓直流 (high voltage direct current transmission, HVDC) 輸電系統可靠性是指HVDC系統在一定時期內可靠輸送電能的能力。HVDC系統傳輸容量很大，一旦發生故障會造成巨大損失，因此，準確量化HVDC系統的可靠性有很大的實際意義。

在直流輸電工程規劃時，一般需要計算規劃方案的可靠性，以評估方案是否達到預定的可靠性要求，進而選擇擴建或加固措施。通常可靠性評估根據拓撲結構、元件可靠性參數(故障率和修復時間)等來估算系統可靠性指標[1-3]。但是，元件可靠性參數通常從歷史故障統計數據中獲得，因此，這些數據往往會受到多種不確定性的影響[4]，目前主要表現在以下3個方面[5]：1) 電力系統中涉及海量統計數據，難免存在無效記錄或數據缺失；2) 元件可靠性參數隨著設備老化會發生變化，若數據更新不及時，會導致可靠性參數不準確；3) 部分場合下人工手動錄入可靠性參數，但人員素質參差不齊，導致可靠性參數不準確。

對于HVDC系統來說，元件可靠性參數的選取直接影響HVDC系統可靠性評估的準確性，甚至影響規劃的直流輸電系統的可靠安全運行[6-7]。另外，對于電網公司而言，錯誤的可靠性評估結果也可能會誤導直流輸電設備的招標[8]。因此，獲得準確的元件可靠性參數是進行可靠性評估的關鍵問題。

目前，國內外學者根據可靠性指標對元件參數的求取和校正已經做了一些研究。

針對大電力系統，文獻[9]運用元件可靠性參數和可靠性指標之間的多重共線性關系，采用偏最小二乘回歸求取原始可靠性參數，但沒有建立可靠性參數和指標之間的數學表達式。文獻[10]針對發電系統，運用多元非線性回歸模型，建立了元件可靠性參數和可靠性指標的關系，但沒有建立可靠性參數和指標之間的函數關系。文獻[11]推導了發輸電系統可靠性指標與可靠性參數之間的數學表達式，可以直觀看到可靠性參數隨可靠性指標的變化情況。文獻[12]建立了電力系統可靠性評估逆問題的解析模型，并將其表示為非線性代數方程組，提出了一種基于區間二分消去法的Krawczyk算子改進算法，克服了在求解過程中選擇合適初始區間的困難。

針對配電網，文獻[13]提出了輻射狀配電系統的逆可靠性評估問題，從已知的系統可靠性指標中尋找未知元件的參數。為此，提出并求解了一個非線性方程組。文獻[14]提出可靠性指標的不確定性評估通常是通過故障率和修復時間中不確定性的傳播來進行的，利用基于故障模式后果分析法的配電網可靠性評估模型，建立可靠性參數與可靠性指標映射關系的可靠性參數求解校正模型。

隨著技術水平的提高，HVDC系統的可靠性指標統計相對準確，通常在系統運行參數、電氣參數及結構等確定后，可以認為元件可靠性參數和系統可靠性指標間具有一一對應的關系[5]。采用可靠性指標求取元件的可靠性參數是一條有效的途徑。然而，鮮有文獻報道通過HVDC系統的可靠性指標求取元件參數的研究。文獻[15]基于可靠性指標隨可靠性參數單調遞增的規律，建立了可靠性最優分解的非線性模型，運用二分法求解了可靠性最優分解問題，然而，該文獻在求解中為簡化計算，設定各元件可靠性按照同一比例變化，這顯然不符合實際。文獻[16]在可靠性最優分解的基礎上，以投資成本最小為目標，從可靠性指標出發，求解可行的元件可用率，從而確定設備選型，達到投資成本最小的目標。文獻[17]建立了元件對直流輸電系統可靠性的最優分解模型，采用二分法求解，并開發出了直流輸電系統可靠性評估平臺。

由上述文獻可以看出，關于HVDC系統由可靠性指標求取元件可靠性參數的一般性研究相對較少。而且，根據HVDC系統可靠性指標求取元件可靠性參數的已有文獻所采取方法的精度有待提高：前述文獻有關大電力系統和配電網等的元件可靠性參數求取的研究中，采取的算法主要分為經典數學規劃算法和智能優化算法兩類。數學規劃算法包括內點法、信賴域反射法等，該類方法非常依賴于良好的初始解，否則只能收斂于局部最優；然而，元件可靠性參數可能的取值范圍較寬，難以給出良好的初值解；智能優化算法的精度難以滿足要求，且面臨陷入局部最優的難題。因此，針對HVDC系統，本文利用全概率公式建立了可靠性指標關于待求元件的解析表達式，基于此提出了由可靠性指標求取元件可靠性參數的解析求解模型，采用基于初始區間二分排除和Krawczyk-Hansen算子的求解算法，在一個較大的可靠性參數初始取值區間內，該方法可以得到所有元件可靠性參數的精確區間解。本文所提出的模型實現了可靠性指標關于元件可靠性參數的解析表達，采用的求解算法避免了前述提到的優化算法陷入局部最優的缺點。最后，本文采用雙12脈動接線HVDC系統進行了算例分析，證明了本文所提模型和算法可以準確求取元件可靠性參數。

1 高壓直流輸電系統可靠性評估模型

1.1 高壓直流輸電系統子系統劃分

HVDC系統中包含海量數目的元件，若直接對所有元件抽樣，會使得可靠性評估具有極大的挑戰性[18]。因此，為降低計算復雜性，本文根據HVDC系統的特點，采用分而治之的方案，將HVDC系統劃分為多個子系統。

本文以圖1所示的雙12脈動接線HVDC系統單線圖為例進行建模分析。該系統由換流變壓器子系統、交流濾波器子系統、直流輸電線路子系統、閥組子系統、直流場子系統組成。下面分別建立各子系統的可靠性評估模型。本文首先假設不考慮換流變壓器備用和平波電抗器備用的影響。

1.2 高壓直流輸電系統子系統可靠性模型

1.2.1 換流變壓器子系統

圖1中，a模塊代表換流變壓器子系統。由a模塊可知：

圖1 雙12脈動接線高壓直流輸電系統子系統劃分示意圖Fig.1 Sketch diagram for subsystem division of HVDC transmission system with double twelve pulse arrangement

1)換流變壓器子系統在每一極上均有12臺換流變壓器，其中Y/Y、Y/△接線各6臺；

2)每個換流閥與不同接線的換流變相連，其中Y/Y、Y/△接線各3臺；

因此，典型元件組停運為單個12脈動換流閥對應的6臺換流變停運[8]，不能直接將換流變壓器子系統等效為多狀態元件進行可靠性評估，本文采用簡化等值方法解決這一問題，考慮到可能計及變壓器備用的影響，本文分別將每個換流閥對應的3臺Y/Y與3臺Y/△接線的換流變壓器等效為1個元件。

由a模塊可知，每個換流閥對應的3臺Y/Y與3臺Y/△接線的換流變壓器之間為串聯結構，根據串聯結構的故障率和修復率等值公式，可得到等值元件故障率和等值修復率，分別如式(1)—(2)所示。

(1)

(2)

式中：n為元件個數，此處取6；c為換流變接線方式，Y/Y型或Y/△型；λi_c和μi_c分別為第i個Y/Y或Y/△型接線換流變壓器的故障率和修復率；λt_c和μt_c分別為一個換流閥對應的換流變壓器的等值故障率和修復率。

1.2.2 交流濾波器子系統

圖1中，b模塊代表交流濾波器子系統，交流濾波器子系統結構如圖2所示。由圖2可知：交流濾波器子系統元件較多，主要包括主母線、小母線、斷路器和交流濾波器；結構相對復雜，但交流濾波是串聯關系，因此，可以根據式(1)、式(2)等效為主母線、小母線、交流濾波器3類元件。但是，實際工程中，往往會投入不同類型和型號的交流濾波器，因此，需要確定交流濾波器子系統的容量狀態，本文采用容量狀態表，介紹如下。

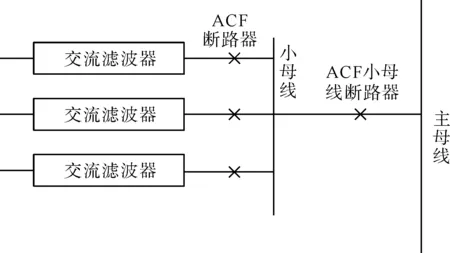
圖2 交流濾波器子系統結構圖Fig.2 Structure diagram of AC filter subsystem

假設有4類交流濾波器，分別用F1、F2、F3、F4表示；各類別數量記為N1、N2、N3、N4。則本文定義投運等效值表示為：Seq=(N1×1 000+N2×100+N3×10+N4×1)，投運等效值和容量狀態一一對應，各種投運情形下的容量狀態都可以通過投運等效值來確定。如F1型交流濾波器故障后，系統等效投運值Seq1=Seq-1 000，再根據投運等值表即可確定系統容量狀態。

1.2.3 直流輸電線路子系統

圖1中，c模塊代表直流輸電線路子系統，其中元件主要為高壓直流輸電線路，因此可直接等效為兩狀態元件。

1.2.4 閥組子系統

圖1中，d模塊代表閥組子系統，它包括同一極的2個12脈動換流閥組，其中每一個12脈動閥組由2個6脈動閥串聯。因此，根據式(1)—(2)可以將每個12脈動閥組等效為兩狀態元件。兩個12脈動閥組間為可靠性上的并聯關系，即任一閥組故障只會導致相應極失去50%的容量。

1.2.5 直流場子系統

圖1中，e模塊代表直流場子系統，其中主要元件為直流濾波器和平波電抗器，2個元件任一個故障均會導致該極停運，因此二者為串聯關系，可以根據式(1)—(2)等效為一個兩狀態元件。

1.3 高壓直流輸電系統可靠性指標

HVDC系統可靠性指標主要包括能量不可用率REU、能量可用率REA、系統期望傳輸容量PEC、單級計劃停運次數FMPOT、單級強迫停運次數FMFOT、雙極計劃停運次數FBPOT等指標。本文主要選用REU、FMFOT和FBPOT指標進行分析，定義如下。

1)能量不可用率

(3)

(4)

TEOT(i)=Ti(1-停運期間可用容量÷PS)

(5)

式中：TS為系統時間尺度；TTEOT為TS內總等值停運時間；TEOT(i)為一年中第i次等值停運時間；N為總停運次數；PS為系統額定容量。

2)單極強迫停運次數

FMFOT指標定義為TS時間內HVDC發生單極強迫停運的次數。

3)雙極強迫停運次數

FBFOT指標定義為TS時間內HVDC發生雙極強迫停運的次數。

1.4 可靠性評估方法

傳統的可靠性評估方法主要分為模擬法和解析法[19]。解析法主要是根據元件參數枚舉狀態求解可靠性指標，置信度高，但不適用于復雜系統；模擬法采用隨機抽樣模擬系統狀態計算復雜適用于大規模系統，其主要方法為蒙特卡羅法。本文采用系統狀態轉移抽樣法。

系統狀態轉移抽樣法是對整個系統的狀態轉移進行抽樣的一種序貫蒙特卡羅方法，重點是確定系統當前狀態的持續時間以及系統的下一狀態及持續時間。通過大量抽樣，最后即可計算得到系統可靠性指標。具體步驟如下。

1)假定元件狀態持續時間服從指數分布，并且初始時刻元件全正常。

2)根據式(6)計算系統狀態持續時間Tk；

(6)

式中：m為當前狀態向外轉移情況總數；U為[0,1]間的隨機數；λi為元件i的狀態轉移率。

3)根據式(7)計算元件j的狀態轉移概率Pj，并根據式(8)得到元件累積轉移概率Pi。

(7)

(8)

4)根據式(8)進行元件狀態轉移定位，如果狀態轉移指標Ch=1，則元件發生狀態轉移，否則，元件狀態保持不變；

Ch=find(Pi>rand(1))

(9)

5)得到一定數量的系統狀態后，計算系統狀態SState。

6)根據式(3)—(5)更新可靠性指標，并統計單極和雙極強迫停運次數。

7)計算方差系數n，如式所示。若n小于一個常數(本文取0.002)，則停止迭代計算，輸出相應的可靠性指標，否則，重復步驟2)—4)，生成新的系統狀態。

(10)

式中T為時間尺度。

2 高壓直流輸電系統元件參數求解解析模型

2.1 元件可靠性參數求解分類

針對根據元件可靠性指標求解元件可靠性參數問題，可能存在以下3種情況：1)已知系統可靠性指標數量大于待求元件可靠性參數數量。2)已知系統可靠性指標數量等于待求元件可靠性參數數量。3)已知系統可靠性指標數量小于待求元件可靠性參數數量。本文僅介紹系統可靠性指標與待求元件可靠性參數數量相同的情況，該情況下方程有唯一解。

假設本文已知的HVDC系統可靠性指標為能量不可用率REU、單極強迫停運次數FMFOT和雙極強迫停運次數FBFOT，待求的HVDC系統元件可靠性參數為元件的故障率和修復率。

2.2 考慮待求元件可靠性參數的可靠性指標解析模型

本文假設能量不可用率REU和單極強迫停運次數FMFOT、雙極強迫停運次數FBFOT已知，元件1的故障率λ1和修復率μ1均未知，元件2的故障率λ2未知，元件3的修復率μ3未知，以此來推導元件可靠性參數求解模型。參數未知的元件個數為3，則這些元件狀態的組合一共有23=8種情況，本文用X表示元件1、2、3的未知參數向量[λ1,μ1,λ2,μ3]，則REU、FMFOT、FBFOT具體推導過程如式(11)—(16)所示。

1)能量不可用率REU的解析模型推導如下。

式中：Ai、Ui(i=1,2,3)分別為穩態可用度和穩態不可用度，Ai=μi/(λi+μi)，Ui=λi/(λi+μi)；

(12)

2)單極強迫停運次數FMFOT的解析模型推導如下。

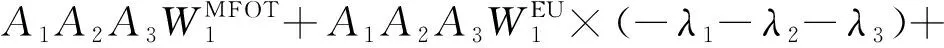
(13)

其中，WiMFOT可表示為：

(14)

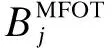
雙極強迫停運次數FBFOT的解析模型推導如下。

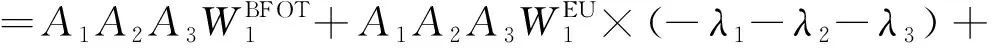
(15)

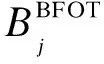
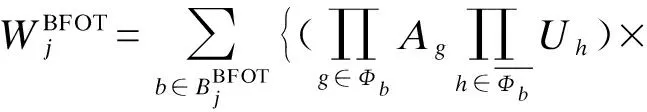
(16)

(17)

式(17)可簡化為式(18)。

F(X)=0

(18)

下面重點解決如何求解非線性方程組式(18)，進而得到HVDC系統元件可靠性參數區間。

3 基于二分排除和Krawczyk-Hansen算子的區間算法的高壓直流輸電系統元件可靠性參數求解模型

針對式(17)或式(18)對應的非線性方程組進行求解，常用點迭代法，雖然該方法計算簡單，但不能直接判斷解的唯一性，除此之外，選取合適的初始值也是運用該方法的關鍵[21]。因此，為解決上述問題，本文提出采用基于初始區間二分排除和Krawczyk-Hansen算子的區間算法求解高壓直流輸電系統元件可靠性參數。

3.1 區間數與區間運算

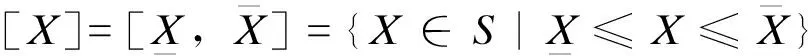
(19)

區間的四則運算定義為：

(20)

(21)

[X]×[Y]=[minS, maxS]

(22)

(23)

(24)

關于區間的其他運算可以參見文獻[20]。

3.2 基于區間二分排除和Krawczyk-Hansen算子的非線性方程組求解的區間迭代法

Krawczyk-Moore算子是在區間Newton法的基礎上發展起來的[21]，算法迭代公式如下。

K(y,X)=y-Yf(y)+[I-YF′(X)](X-y)

(25)

y=m(X)

(26)

Y=[m(F′(X))]-1

(27)

Hansen在迭代中改進Krawczyk-Moore算子，得到Krawczyk-Hansen算子：

H(y,X)=y-Yf(y)+L(X)(H′-y)+
U(X)(X-y)，y∈X

(28)

H′=H(y,X)∩X

(29)

(30)

m(X)=(m(X1),m(X2),…，m(Xn))T

(31)

式中：X為區間向量；m(X)為區間向量X的中點；I為n階單位矩陣；Y為n階非奇異矩陣；L(X)和U(X)分別為區間矩陣[I-YF′(X)]的下三角矩陣和上三角矩陣。

當所研究的區間過大時，Krawczyk-Hansen算子往往無法有效判定該區間上是否存在解[22]，為了解決這個問題，本文采用二分排除縮小區間的寬度，使得Krawczyk-Hansen算子能夠判定細分區間上解的情況。

因此，基于區間二分排除和Krawczyk-Hansen算子的非線性方程組求解的區間迭代法算法流程如下。

1)令[X]=[X]0∈I(Rn)， 初始化二分區間表B， 解區間表T。初始化二分變量序號b=1、二分區間表長度l=1，給定解區間的收斂精度ε和ξ， 初始化區間寬度系數α。

2)根據Krawczyk-Hansen算式(28)—(31)計算H(X)和Z=X∩H(X)。

3)根據Z和X的包含關系判斷解的存在性和唯一性。若Z=?，則轉流程6)；若W(X)屬于X，則在X上有解，轉流程4)；若W(Z)<αW(X)，則X=Z，轉流程2)；否則，轉流程5)。

4)以m(X)為初值，利用點Newton法迭代計算，可得方程組的一個解X*，并存入表T。

6)若l=0，則轉流程7)。從區間表B取出排在首部的區間賦給X，l=l-1，轉流程2)。

7)輸出表T中的全部解區間。若T為空集，則該方程組無解。

4 算例分析

4.1 算例簡介

本文以雙12脈動接線的HVDC系統作為算例，進行可靠性評估分析。雙12脈動接線的高壓直流輸電工程示意圖如圖1所示。逆變側和整流側共有24臺換流變，4組閥組，還包含平波電抗器、交流濾波器等，其中，平波電抗器有3種型號。各元件原始參數如表1所示[1]，本文利用狀態轉移抽樣法計算可靠性指標。并以該指標作為輸入，利用本文的可靠性參數校正模型求解得到相應的可靠性參數。

表1 雙12脈動接線特高壓直流輸電系統可靠性參數Tab.1 Reliability parameters of HVDC power transmission system with double twelve pulse connection

4.2 可靠性評估結果

本文采用狀態轉移抽樣法計算雙12脈動接線高壓直流輸電系統的狀態停運容量，結果如表2所示，表中分別給出了各故障容量狀態下的狀態概率和頻率指標。雙12脈動接線高壓直流輸電系統可靠性指標計算結果如表3所示。

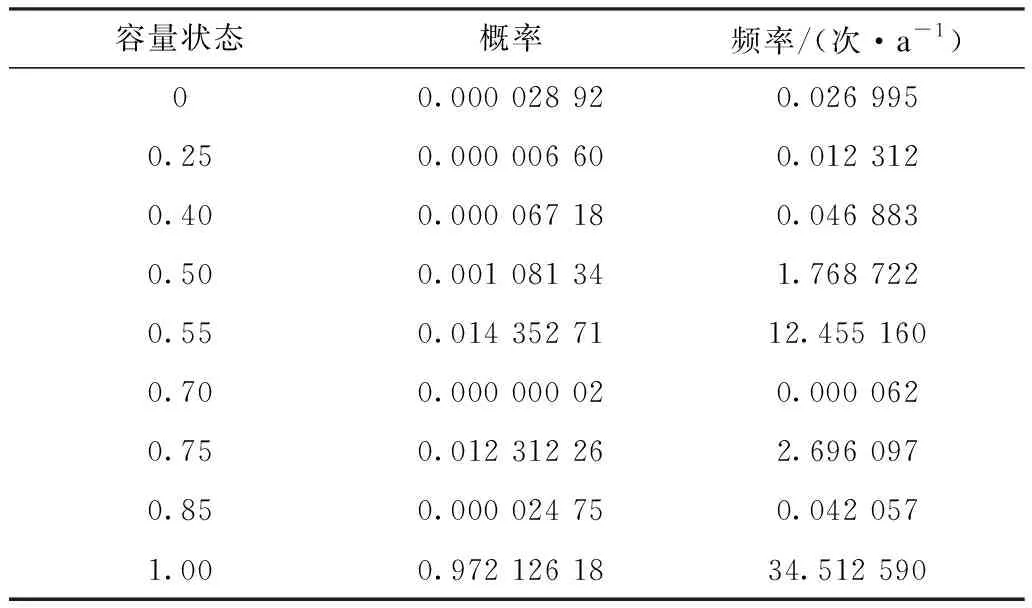
表2 雙12脈動接線高壓直流輸電系統容量狀態對應概率和頻率計算結果Tab.2 Caculation results of probability and frequency of corresponding capacity of double twelve pulse HVDC

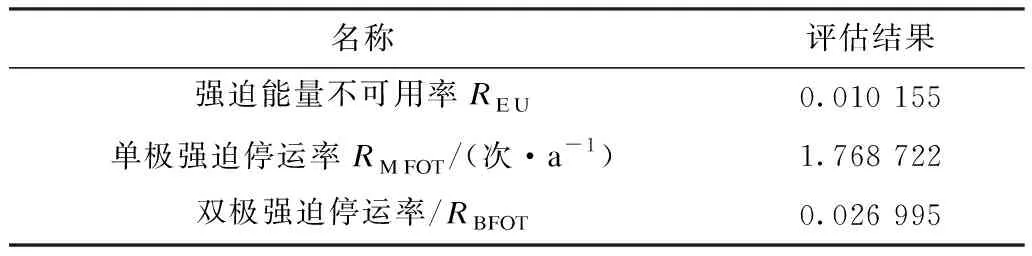
表3 雙12脈動接線高壓直流輸電系統主要可靠性指標評估結果Tab.3 Assessment results of main reliability indexes of double twelve pulse HVDC power transmission system

從表3可以看出，雙12脈動接線系統的可靠性比較高，這是由于雙12脈動接線系統的單側單極有4個換流單元，只故障1個換流單元并不會導致該極完全停運。

4.3 可靠性參數解析模型求解結果分析

以4.2節計算得到的REU、RMFOT和RBFOT指標作為已知參數，代入本文的基于初始區間二分排除和Krawczyk-Hansen算子的HVDC系統元件可靠性參數求解模型中，求解元件可靠性參數。

本文假設換流變壓器、直流輸電線和直流濾波器的故障率分別為λ1、λ2、λ3，修復率分別為μ1、μ2、μ3。將可靠性參數區間的最大值均放大為真實指標的2倍，最小值縮小為原來的1/2，下面設置4個算例來驗證本文所提模型的正確性和有效性。

Case1：當強迫能量不可用率、單極強迫停運率、雙極強迫停運率3個可靠性指標只有1個已知時，求取λ1、λ2、λ3、μ1、μ2、μ3中任意1個元件可靠性參數，求解結果如表4所示。

表4 Case1參數求解計算結果Tab.4 Calculation results of parameter solution in case 1

Case2：當強迫能量不可用率、單極強迫停運率、雙極強迫停運率3個可靠性指標已知任意2個時，求取λ1、λ2、λ3、μ1、μ2、μ3中任意2個元件可靠性參數的組合，求解部分結果如表5所示。

表5 Case2參數求解計算結果Tab.5 Calculation results of parameter solution in case 2

Case3：當強迫能量不可用率、單極強迫停運率、雙極強迫停運率3個可靠性指標均已知時，求取λ1、λ2、λ3、μ1、μ2、μ3中任意3個元件可靠性參數的組合，求解部分結果如表6所示。

表6 Case3參數求解計算結果Tab.6 Calculation results of parameter solution in case 3

Case4：當強迫能量不可用率、單極強迫停運率、雙極強迫停運率3個可靠性指標均已知時，運用遺傳算法求解λ1、λ2、λ3、μ1、μ2、μ3。結果如表7所示。

表7 Case4參數求解計算結果Tab.7 Calculation results of parameter solution in case 4

將表4—6的可靠性參數計算結果與表1中元件可靠性參數相比可知：無論是利用單個可靠性指標求解單個元件可靠性參數，還是利用多個可靠性指標求解元件可靠性參數的組合，本文提出的區間二分和Krawczyk-Hansen算子的區間算法計算得到的元件可靠性參數均被壓縮在一個很小的取值區間內，并且包含表1中元件給出的可靠性參數，因此，表4—6的結果證明了所提算法能有效準確地求解出對應的元件可靠性參數。本文定義求解精度為參數解區間與真值的誤差。經計算，各元件可靠性參數區間結果的精度均可以達到10-5，不同取值的同類型參數的求解結果達到了相似的精度，這說明求解精度與待求元件可靠性參數本身數值大小無關。同時，由表4—6可以發現，對于同一組待求的可靠性參數，采用不同的可靠性指標的組合，則求解得到的元件可靠性參數的精度不同。

表7為基于遺傳算法求解方程得到的元件可靠性參數結果。比較表7結果和表1的參數給定值可以發現，遺傳算法計算得到的結果存在顯著誤差。

以元件1的故障率和修復率為例：通過REU指標求解得到的元件1的故障率和修復率區間分別為[0.021 19, 0.021 21]、[65.779 99, 65.780 01]，最大相對誤差分別為0.047 2%以及0.000 015 2%；通過REU和RMFOT計算得到的元件1的故障率和修復率分別為[0.021 19, 0.021 21]、[65.780 00, 65.780 01]，最大相對誤差分別為0.047 2%以及0.000 015 2%；通過REU、RMFOT、RBFOT計算得到的元件1的故障率和修復率為[0.021 20,0.021 20]、[65.775 75, 65.785 90]，最大相對誤差分別為0以及0. 008 97%。遺傳算法求解得到的故障率為0.021 17，相對誤差為2.12%，修復率為65.679 1，相對誤差為0.153 4%。

通過上述計算的相對誤差可以發現以下兩點。

1)相對于Case1和Case2，已知系統可靠性指標數目為3(即Case 3)時，求解結果的誤差比較大，這是因為Case3的情況有多個待求修復率，而強迫停運率指標關于修復率參數的靈敏度很小。針對待求元件可靠性參數中存在多個修復率時得求解精度會較差這種情況，可以有2種方法提高求解精度。

(1)給出可靠性參數的良好的初始取值區間；

(2)減小區間算法中設置的最小允許區間分割寬度。

2)相對于本文提出的區間二分和Krawczyk-Hansen算子的區間算法，基于遺傳算法的元件可靠性參數求解結果的誤差較大。這說明遺傳算法容易陷入局部收斂，達不到全局最優。作為對比，本文所提模型能夠得到包含元件可靠性參數真值的精確區間。

5 結論

本文首先采用狀態轉移抽樣法對雙12脈動接線高壓直流輸電系統進行可靠性評估。再基于可靠性參數與可靠性指標的映射關系，利用全概率公式推導了HVDC系統可靠性指標與元件可靠性參數之間的解析函數，最終建立了基于初始區間二分排除和Krawczyk-Hansen算子的HVDC系統的元件可靠性參數求解模型，對元件可靠性參數進行校正。

基于雙12脈動接線的HVDC系統的測試驗證了本文模型的正確性和有效性。計算結果表明，本文所提模型能夠精確地求解得到HVDC系統主要元件的可靠性參數，而且求出的可靠性參數區間的誤差要小于遺傳算法的求解誤差，解決了遺傳算法依賴初始區間、求解精度不高的問題。