支撐劑在交叉裂縫中運移規律的數值模擬

曾軍勝 ，戴城 ，方思冬 ，李恒 ，劉華

（1.中國石化石油勘探開發研究院，北京 100083；2.中國地質大學（武漢）資源學院，湖北 武漢 430074）

0 引言

近年來，非常規氣藏的開發受到越來越多的關注和重視。2020年，我國頁巖氣產量達到了200多億立方米，同比增長高達30%，成為天然氣增產的主力。這得益于水平井和水力壓裂2項關鍵技術的快速發展和成熟應用。而水力壓裂體系涉及一個至關重要的流體-顆粒兩相流問題——支撐劑運移［1-3］。采用支撐劑能夠有效避免水力裂縫的閉合，從而維持有效傳導率。而支撐劑在裂縫中的運移和分布情況，則直接影響水力壓裂改造后儲層的有效傳導率。因此，研究支撐劑運移過程對水力壓裂的效果評估和方案設計有重要意義。

通常，支撐劑運移發生在水力壓裂產生的復雜縫網當中。如何改善支撐劑在縫網中的鋪置效率，使更多的支撐劑進入支縫，成為現場施工方案設計的重點問題。以往大多數的文獻主要采用物理實驗［4-7］和數值模擬［8-9］這兩大類方法研究支撐劑在單一裂縫中的運移規律。考慮的各類因素包括攜砂液和支撐劑顆粒的物性參數、施工方案、支撐劑體積分數、裂縫擴展及流體濾失等。這些研究對揭示支撐劑在裂縫中沉降和運移的基本規律具有十分重要的作用。

針對支撐劑在縫網中的運移規律，近年來國內外的相關研究也呈現逐年增長的趨勢。Sahai等［10-12］利用物理實驗方法，研究了支撐劑在復雜縫網中的運移規律。但是物理實驗周期往往較長，同時能夠獲取的數據十分有限。目前，數值模擬已成為研究支撐劑運移的有效方法。郝麗華等［13-14］采用雙流體模型，模擬了大尺度下支撐劑在縫網中的鋪置情況。

支撐劑運移本質上是一類流體與顆粒強耦合作用的兩相流問題。為了闡明支撐劑運移涉及的物理機制，需要在物理建模時充分考慮其關鍵機理。在支撐劑運移過程中，支撐劑顆粒之間的作用、裂縫壁面對顆粒的作用、攜砂液與顆粒之間的相互作用是十分重要的。本文結合目前流行的流體-顆粒兩相流的數值模擬方法，即計算流體力學-離散元方法（Computational Fluid Dynamics-Discrete Element Method，簡稱 CFD-DEM 方法）［15-16］，對支撐劑在交叉裂縫中的運移過程進行研究，分析裂縫交角及攜砂液黏度對支撐劑運移規律的影響。CFD-DEM方法基于拉格朗日框架刻畫顆粒的演化，能夠準確刻畫顆粒與顆粒/壁面及流體與顆粒之間的相互作用。與雙流體模型相比，CFD-DEM方法在物理建模上具有天然優勢，能夠捕捉更多的運移細節。

本文旨在研究支撐劑顆粒在交叉裂縫中的運移機理，包括顆粒堆積、聚團等效應，同時定量考察在不同條件下支撐劑流入支縫的比例，以便直觀理解。下面分別從CFD-DEM方法、裂縫交角及攜砂液黏度3個方面，對支撐劑在交叉裂縫中的運移規律展開討論。

1 CFD-DEM方法

1.1 流體及顆粒的控制方程

在CFD-DEM方法中，流體控制方程為體積平均納維-斯托克斯（VANS）方程［17］：

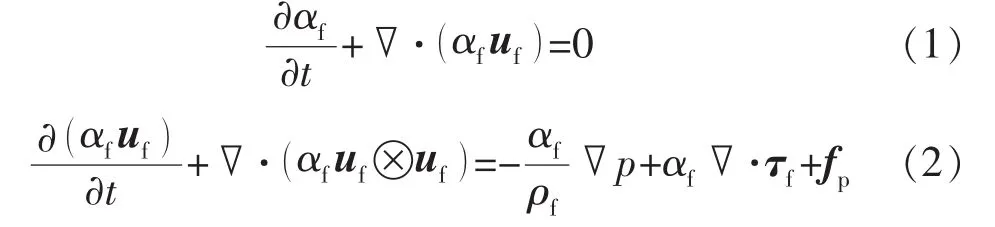
式中：αf為流體體積分數；t為時間，s；▽為梯度算子；▽·為散度算子；uf為流速，m/s；ρf為流體密度，kg/m3；p為流體壓力，Pa；τf為流體黏性應力張量，Pa；fp為流體與顆粒相互作用（特指拖曳力）產生的動量源匯項，m/s2。

式（1）和（2）分別為流體的連續性方程和動量方程，這里假設流體為不可壓縮牛頓流體。

在CFD-DEM方法中，顆粒參數是基于DEM方法［18］進行求解的。在DEM方法中，支撐劑顆粒被建模為彈性圓球，顆粒之間的作用力通常基于軟球模型進行計算。如圖1所示（其中，i，j為顆粒編號，δn為重疊量），當圓球之間發生重疊時，認為接觸點處存在彈簧和黏壺，二者進行并聯后，產生一個綜合的作用力。通過這種方式可以考慮顆粒之間的非彈性碰撞。

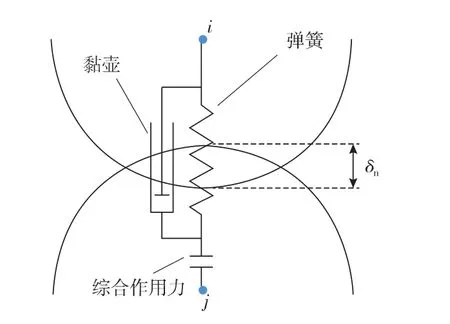
圖1 軟球模型示意

支撐劑顆粒的運動是基于拉格朗日框架進行描述的，這與描述流體運動的歐拉框架不同，因此CFDDEM方法是一類歐拉-拉格朗日框架混合方法。顆粒的運動遵循牛頓第二定律，可以表述為

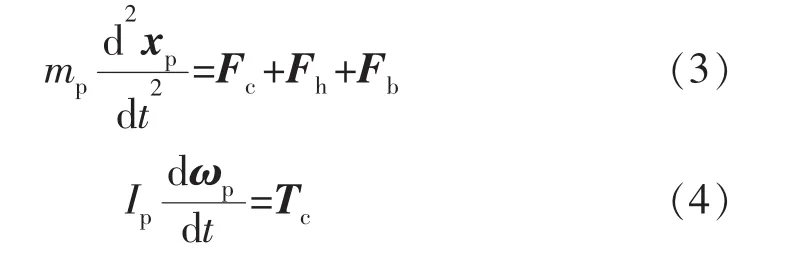
式中：mp為顆粒質量，kg；xp為顆粒位移，m；Fc，Fh，Fb分別為顆粒運動中所受到的顆粒與顆粒/壁面的碰撞力、流體與顆粒耦合的水動力及體積力，N；Ip為顆粒轉動慣量，kg·m2；ωp為顆粒角速度，rad/s；Tc為顆粒碰撞過程中產生的力矩，N·m。

式（3）和（4）分別刻畫了顆粒的平動方程和轉動方程。

1.2 流體與顆粒耦合策略

本文的支撐劑數值模擬是基于開源軟件CFDEM實現的［19］，其采取的耦合方法為目前主流的四路耦合策略［20］，這一點從式（1）—（4）也能夠得到體現。所謂四路耦合，指的是考慮了流體體積分數對流體控制方程的影響、流體對顆粒的作用、顆粒對流體的反饋作用及顆粒之間的碰撞作用4個方面。

考慮到拖曳力、流體壓力梯度力及黏性應力梯度力對水動力的影響，式（3）中的水動力可以表述為

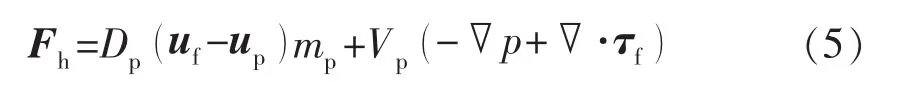
式中：Dp為拖曳力系數，s-1；up為顆粒運動速度，m/s；Vp為顆粒體積，m3。

本文采用Wen&Yu模型計算Dp：

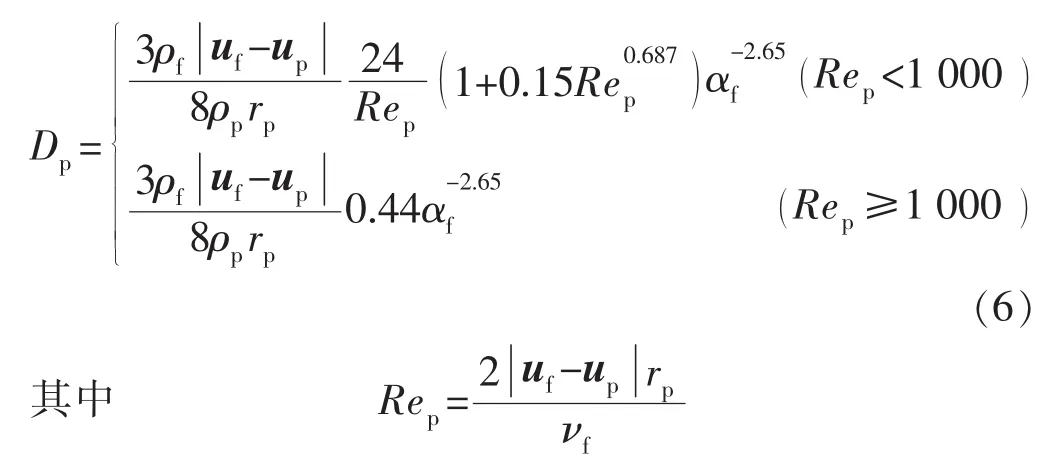
式中：ρp為顆粒密度，kg/m3；rp為顆粒半徑，m；Rep為顆粒雷諾數；νf為流體運動黏度，m2/s。

值得注意的是，CFD-DEM方法作為歐拉-拉格朗日混合框架，與常見的雙流體模型相比，在具體實現上需要克服混合框架帶來的難點。首先，需要利用插值函數完成歐拉網格與拉格朗日點之間的信息交互；其次，流體運動和顆粒碰撞的特征時間是有差別的，流體的計算步長限制通常比顆粒計算步長要大得多。因此，實際耦合過程中，往往采用一步流體計算、多步顆粒計算的顯式耦合策略。

1.3 模擬區域及參數設置

本文所模擬的交叉裂縫如圖2所示。左側為攜砂液和支撐劑的入口，主流動方向為水平向右，在經過主縫、支縫交叉處時，攜砂液及支撐劑發生分流，沿相應的方向流動，直至出口。入口采用定流量的邊界條件，出口采用定壓的邊界條件，具體模擬參數見表1。

表1 交叉裂縫中支撐劑運移的模擬參數

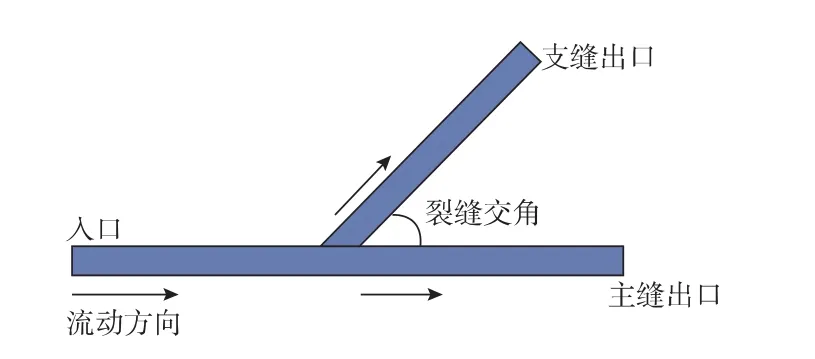
圖2 交叉裂縫空間俯視圖

在本文算例中，主縫寬度設計為5.0 mm，支縫寬度設計為主縫寬度的一半，即2.5 mm，這主要是考慮到實際情況下支縫寬度通常比主縫小。為了捕捉支撐劑顆粒在裂縫交叉處的運移細節，需要針對流體網格進行局部加密；同時主縫、支縫在遠離交叉處的區域，采取逐漸粗化的網格進行模擬，從而降低整體網格數量，進而降低計算量。

2 裂縫交角對支撐劑運移規律的影響

在裂縫交角 θ分別為 45°，90°，135°的條件下，重點考察了支撐劑在攜砂液黏度為1 mPa·s時的鋪置情況（見圖3）。紅色區域代表支撐劑高速運移的懸浮區域；藍色區域的支撐劑顆粒運動速率接近0，可以認為是砂床堆積區域。

圖3 低黏條件下支撐劑在不同裂縫交角時的鋪置情況

對比圖3中的3種情況，可以看出以下運移規律：

1）在攜砂液黏度為1 mPa·s的條件下，支撐劑在主縫存在顯著沉降。在該算例中，顆粒的沉降速率約為0.134 m/s，因此當不存在顆粒堆積和重力對流作用時，支撐劑的沉降界面（懸浮區域與清水的交界面）斜率接近1/8；而在重力對流的作用下，實際沉降界面斜率明顯大于1/8。

2）支撐劑在主縫中的運動速率顯著高于支縫。高速流動的紅色懸浮區域占主縫前半段的比例明顯高于藍色堆積區域。同時,經過裂縫交叉處后，支撐劑在主縫的后半段發生明顯堆積，形成藍色的靜止砂床區域。這是由于在經過裂縫交叉處后，部分流體進入支縫，主縫中的流速驟降，支撐劑在豎直方向上更加容易發生沉降。

3）在不同的裂縫交角條件下，主縫中支撐劑運移狀態差異較小，而在支縫中，隨著裂縫交角增大，支撐劑進入支縫的比例明顯下降。這一效應主要是流體/顆粒的慣性作用導致的。裂縫交角越小，流體/顆粒越容易在慣性作用下進入支縫；而當裂縫交角大于90°時，紅色懸浮區域中的支撐劑必須通過在裂縫交叉處發生碰撞、旋轉等復雜運動，才能少部分流入支縫當中。

為了定量考察支撐劑在裂縫交叉處的分流規律，分別統計了上述3種情況下支撐劑進入支縫的比例（見表2）。可以看出，在攜砂液黏度為1 mPa·s的條件下，隨著裂縫交角增大，支撐劑進入支縫的比例是不斷下降的。在45°時，支撐劑進入支縫的比例約在1/4；在90°時，支撐劑進入支縫的比例降為1/6左右；在135°時，支撐劑進入支縫的比例降為1/14左右。

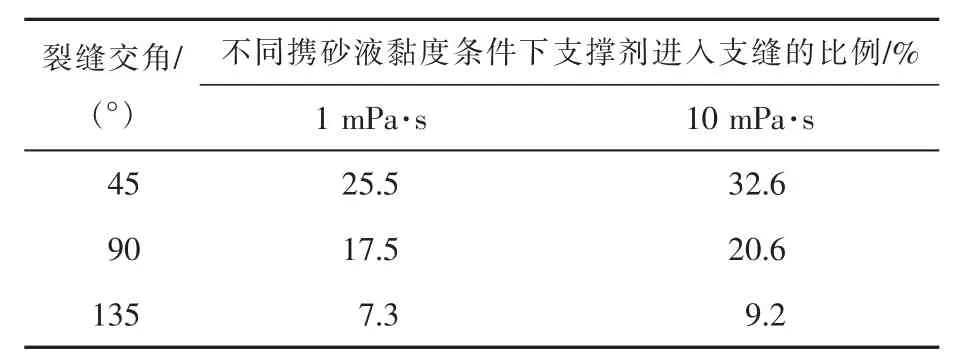
表2 支撐劑進入支縫的比例

從圖3可以明顯看出，在主縫的后半段和支縫中，存在大量藍色砂床堆積區域。將圖3b放大，展示了支撐劑顆粒在裂縫交叉處的堆積細節（見圖4）。從圖4b可以看出，支撐劑在堆積區域中的排列方式是十分精確、真實的。這表明采用CFD-DEM方法模擬支撐劑運移過程，確實能夠捕捉到很多其他數值方法所不能刻畫的細節。

圖4 裂縫交叉處支撐劑顆粒的堆積細節

3 攜砂液黏度對支撐劑運移規律的影響

攜砂液黏度為1 mPa·s時，支撐劑在運移過程中有明顯堆積行為。這里將攜砂液黏度提高至10 mPa·s，進一步考察攜砂液黏度對支撐劑在交叉裂縫中運移規律的影響，以及提高攜砂液黏度能否提高支撐劑進入支縫的比例。圖5展示了攜砂液黏度為10 mPa·s條件下支撐劑的鋪置情況。同樣模擬了3種裂縫交角條件下的情況，與低黏條件下的算例一一對應。支撐劑進入支縫的比例如表2所示。

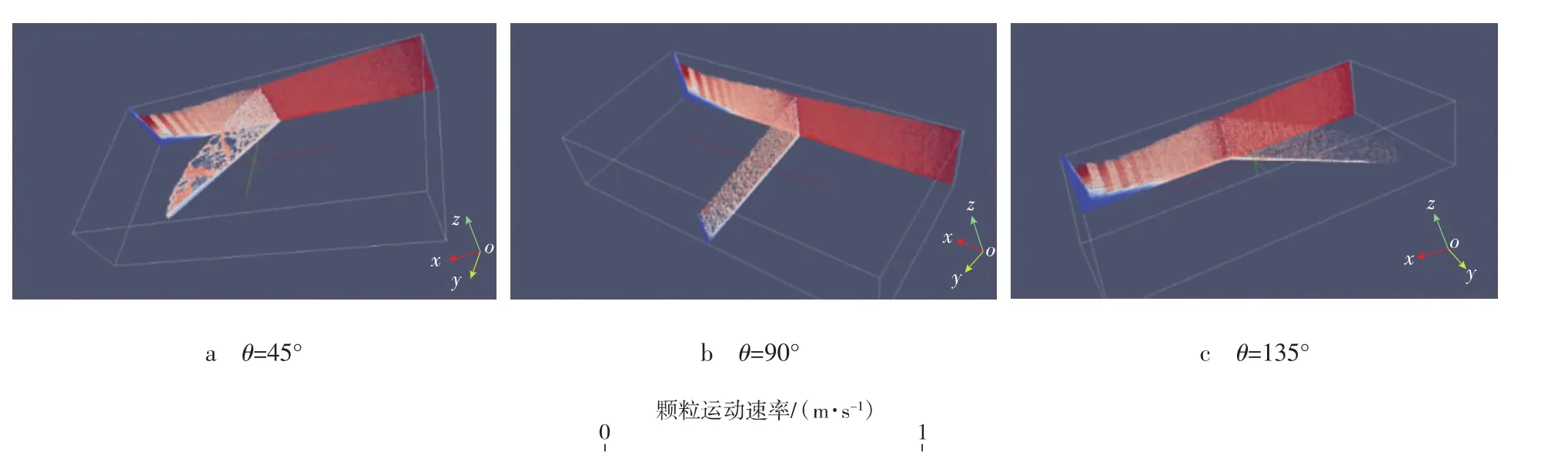
圖5 高黏條件下支撐劑在不同裂縫交角時的鋪置情況

通過比較圖5和圖3展示的鋪置情況，可以看出提高攜砂液黏度后支撐劑運移規律的主要變化。

1）支撐劑在主縫中的水平運移能力明顯提高。在提高攜砂液黏度后，懸浮區域的沉降界面斜率顯著減小。在攜砂液黏度為10 mPa·s的條件下，顆粒的沉降速率約為0.052 m/s，約為低黏條件下沉降速率的40%。因此，紅色懸浮區域幾乎占據主縫前半段的大部分區域，在主縫后半段，顆粒堆積也主要發生在出口附近。

2）支撐劑在支縫中的運移方式發生明顯改變，懸浮區域在支縫中的占比明顯提高。支撐劑沉降速率的大幅降低，同樣有利于它在支縫中的運移。與低黏條件下的運移情況不同，在高黏條件下，主縫懸浮區域中的支撐劑經過裂縫交叉處之后，依然能夠整體保持懸浮狀態，繼續沿支縫方向運移。從定量角度看，高黏條件下支撐劑進入支縫的比例確有明顯提高（見表2）。

3）相比于低黏條件，高黏條件下支撐劑在支縫中的宏觀運移狀態發生明顯變化，出現聚團效應。對比圖3a與圖5a可以發現，在高黏條件下，支縫中懸浮區域內支撐劑的分布更容易演化出空間非均勻性，即聚團效應。細節如圖6所示，其中攜砂液黏度為10 mPa·s，裂縫交角為45°。從圖6可以看出，這種空間非均勻性是在支撐劑進入支縫后不斷演化出來的。在靠近交叉處，支撐劑分布的非均勻性結構的尺度很小；而隨著支撐劑逐漸向支縫內部運移，這種非均勻性結構的尺度不斷加大。這一效應主要是顆粒誘導的流體不穩定造成的。

圖6 高黏條件下支撐劑在支縫內運移產生的聚團現象

4 結論

1）隨著裂縫交角增大，支撐劑進入支縫的比例不斷下降。

2）提高攜砂液黏度，能夠明顯提高支撐劑進入支縫的比例。低黏條件下，支撐劑進入支縫的主要路徑是基于懸浮區域分流及砂床遷移機制完成的；而高黏條件下，支撐劑進入支縫的主要路徑是通過懸浮區域分流機制完成的。

3）CFD-DEM方法能夠精確刻畫支撐劑顆粒之間的相互作用，因此可以用于研究砂床堆積的物理機制及運移過程中的聚團效應。

4）本文僅考慮了裂縫交角及攜砂液黏度對支撐劑在交叉裂縫中運移規律的影響。事實上，還有許多其他的重要因素及復雜工況尚待研究，包括支撐劑密度、粒徑分布、非牛頓流體、復雜縫網等。今后應進一步考察這些情況，揭示相關規律。