非廣延氣體中分子碰撞頻率和平均自由程的研究*

鄭亞輝,董曉曦,孫朋強

(河南工學院 理學部,河南 新鄉 453003)

0 引言

碰撞是分子運動論中最基本的物理過程。在碰撞過程中分子之間彼此交換能量和動量,是氣體在宏觀上體現出來的各種輸運過程的微觀機制。碰撞頻率及其相關的平均自由程是氣體輸運如擴散、熱傳導過程中的重要特征量,直接決定了輸運的時空尺度,即輸運的快慢問題。對于經典氣體中的分子碰撞頻率和平均自由程問題,很多文獻已經討論過了[1-2],相應結果已經進入教科書中。

現代科學的特點是研究領域不斷向具備多自由度和多重復雜特征的系統延伸。科學研究和技術發展的實踐表明,在這些復雜系統中,經典的玻爾茲曼統計理論已經不適用了。經濟社會進一步發展的需求,推動了新的統計理論的誕生和發展。這個新的統計理論叫非廣延統計力學,1988年由巴西物理學家C.Tsallis首次提出[3]。該統計理論是經典玻爾茲曼統計在具有長程相互作用或關聯的系統的推廣,其基本的分布函數不是指數型的,而是冪律型的。該分布函數已經在等離子體和天體物理觀測中得到證實[4-8]。此外,在其他類型的復雜系統中,如反常擴散系統[9-10]、生化系統[11-13]、地震預測[14]和股票市場[15]等,都出現了冪律形式的分布函數。

如果需要考慮分子間的范德瓦爾斯力對氣體整體性質的影響,除了引入維里修正、建立范德瓦爾斯方程方法外,另一種可選擇的方法是將非廣延統計理論引入對這種氣體的研究中。應用該理論的要點是,將分子間作用力與系統整體的長程關聯聯系起來,并用非廣延參數描述這種關聯特征。這種長程關聯化的氣體叫做非廣延氣體,它與實際氣體在某種程度上可以等效[16-17]。

本文主要研究非廣延氣體中分子碰撞頻率和平均自由程問題。

1 系綜分布函數與雙粒子分布函數的導出

考慮一個非廣延正則系綜。在該正則系綜所描述的系統中,哈密頓量除包含動能項外,還包含一個與分子間作用力有關的勢函數。需要注意,該勢函數不是引力勢,不會引起整體的不均勻性,只是造成了幾個自由程范圍內氣體分子的關聯。通過標準的熵極化方法,可以得到該非廣延正則系綜的分布函數,即廣義吉布斯函數[18],形式為

(1)

其中β'是廣義拉格朗日乘子,它對應的溫度是不可測量的;E是系統能量;q是非廣延參數,它對1的偏離代表了系統的非廣延程度。所謂非廣延是針對廣延而言的,指的是系統的熵不具有可加性。

采用連續能量分布,(1)式中的配分函數定義為

(2)

我們已經假定系統的粒子數是2N。系統的勢函數代表了氣體分子之間的弱關聯。如果只考慮分子二體碰撞,氣體分子發生二體碰撞時其他分子的影響可以忽略不計。這時整個系統可以看成是大量雙粒子結構的集合體,因此總能量可以寫成

(3)

其中U代表雙粒子結構中分子的總勢能。每個雙粒子結構的能量都是一個隨機量,這些結構在系統中各個位置出現的概率是相同的,因此上式可以等效成如下形式

(4)

采用如下參數變換[18],

(1-q)N=1-ν

(5)

則配分函數可以寫成

(6)

其中雙粒子分布配分函數定義為

(7)

因此雙粒子分布函數為

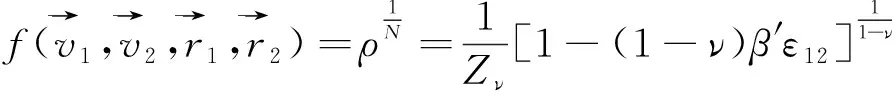
(8)

在給定坐標系中,雙粒子結構的質心和相對位置可定義如下

(9)

二體碰撞可能在系統的任何位置發生,因此相互作用勢能必定是質心和相對位置的函數

(10)

其中,第一項是由長程弱關聯引起的勢能,第二項是二體碰撞勢能,可取成列納德-瓊斯勢[19]的形式

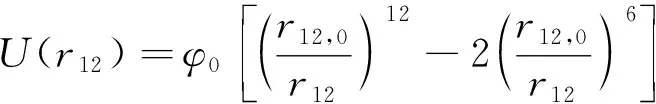
(11)

在這里,r12,0和φ0是兩個特征參量,前者表示勢能最小的位置。平均來說,分子間平均距離總是要讓體系的勢能最小,因此可將(11)式取在最小勢能位置。則有

(12)

(13)

上面的結果對于任意有限的分子間距積分都成立。為了以后使用方便,我們已經讓分布函數f歸一化為系統的粒子數。此時的配分函數為

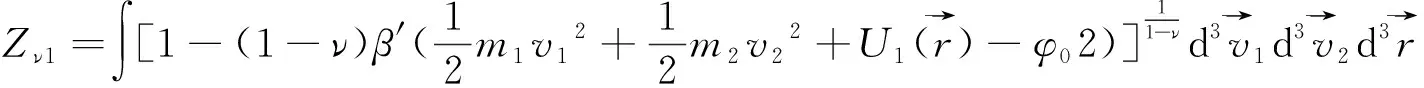
(14)

現在需要對分布函數(13)做進一步修改,為此令

(15)

定義

(16)

則有

(17)

其中

(18)

式(17)正是我們想要的雙粒子分布函數,其中的可測量溫度T在引力系統是位置的函數,在弱關聯系統只在局部區域跟位置有關,在整體上是均勻的;n(r)代表系統粒子的數密度。該式也可以通過廣義H定理得到。

2 氣體分子相對速率分布函數與碰撞頻率

我們用相對速率分布函數計算分子碰撞頻率。為了得到相對速率分布函數,定義二體碰撞的質心速度和相對速度如下

(19)

雙粒子結構的總動能為

(20)

其中

(21)

因此有

(22)

相對速度分布函數

(23)

歸一化系數

(24)

對單一組分氣體,相對速率分布函數

(25)

m代表分子質量。

根據上式,在體積元dxdydz內,相對速率在v12～v12+dv12范圍內的分子數為

(26)

如圖1所示,在xy平面內取一面元dS,在體積元dxdydz內,只有那些沿著所示圓錐角運動的分子才能碰到dS面上。此圓錐所包含的立體角是

(27)

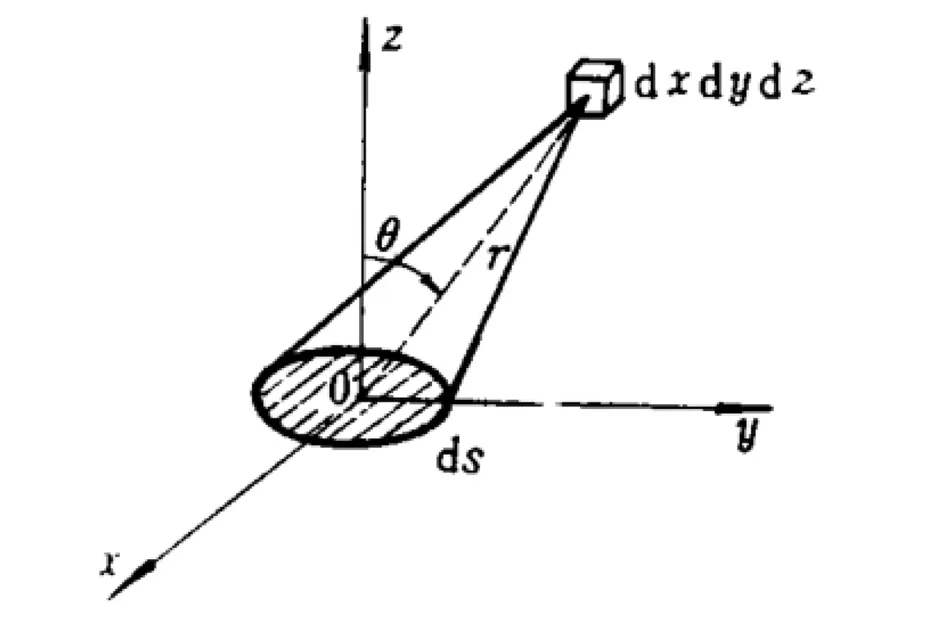
圖1 分子碰撞示意圖

因此,在體積元dxdydz內及彼此之間的相對速率在v12～v12+dv12范圍內,且能碰到面元dS分子數,在球坐標系中的表達式為

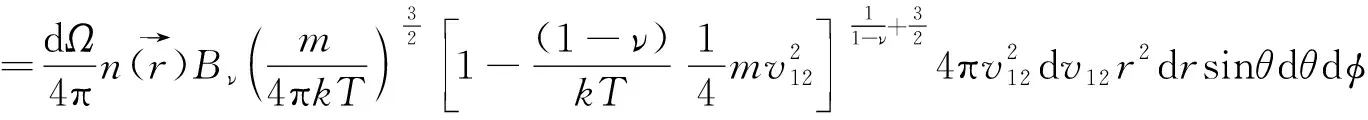
(28)

以任意相對速率,在單位時間內對單位面積的碰撞次數

(29)

其中的無量綱系數

(30)

在非廣延氣體中,我們仍然使用剛性分子模型。一個直徑為d的剛性分子,其俘獲截面可表示為S=4πd2。所以,單位時間內其他氣體分子與該分子的碰撞次數即碰撞頻率為

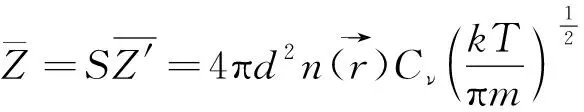
(31)

可以發現,該表達式與經典結果中的碰撞頻率公式[1-2]之間只差了一個跟非廣延參數有關的修正系數。當ν→1時,式(31)趨于經典碰撞頻率的表達式。

3 單粒子分布函數與平均自由程

單純由式(31)無法計算氣體分子的平均自由程。為此先要得到非廣延氣體的單粒子分布函數。通過非廣延系綜方法,利用與(5)相似的變換關系,可以得到單粒子分布函數[18],通過廣義H定理[20]也能得到該函數,其具體形式為

(32)

歸一化系數

(33)

利用非廣延統計力學中的關于平均值的標準定義[21-22],氣體分子的平均速率由下式給出,即

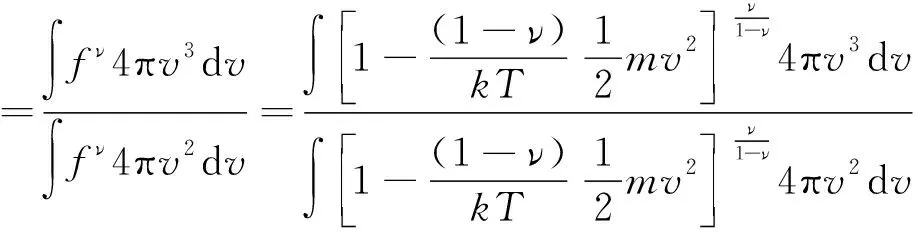
(34)

很顯然當ν→1時,上式趨于經典平均速率公式。按照平均自由程的定義,由(34)/(31),可得

(35)

其中的無量綱系數為

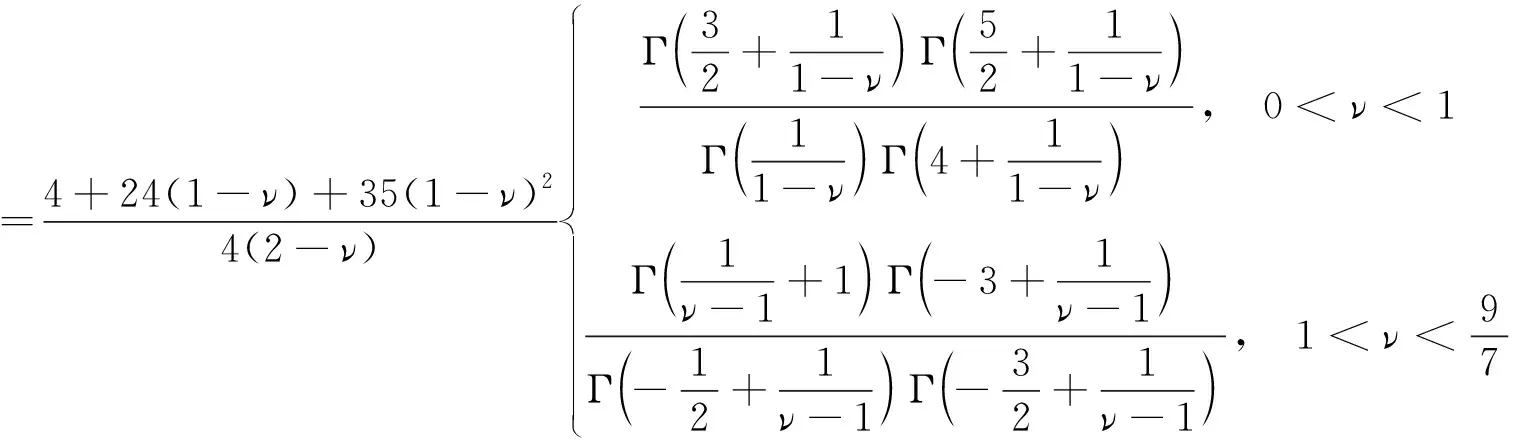
(36)

上式表明,隨著非廣延參數偏離1越來越遠,非廣延氣體的平均自由程會越來越偏離其經典數值。很明顯,無論是無量綱系數(30)還是(36),都代表了在非廣延統計中的理論結果與經典統計中理論結果的比值。為了看清楚非廣延參數對理論結果的影響,我們分別對兩者進行了數值計算,并將二者隨非廣延參數變化的曲線畫在了圖2和圖3中。可以發現,當非廣延參數趨于9/7時,碰撞頻率趨于無窮大,同時平均自由程趨于零。另一方面,當非廣延參數趨于零時,碰撞頻率比趨于0.46,比1小了很多,平均自由程比則趨于1.45,比1大很多。

圖2 碰撞頻率比隨非廣延參數變化曲線

圖3 平均自由程比隨非廣延參數變化曲線

數值計算和曲線模擬的結果表明,非廣延參數大于1,反映了分子間吸引力對氣體整體性質的影響,它造成碰撞頻率增加,分子的自由程變短。非廣延參數小于1,反映了分子間斥力對氣體性質的影響,它造成了碰撞頻率一定程度的減小,分子自由程則相應增加。對于經典理想氣體來說,分子間作用力對氣體性質沒有任何影響,對應于非廣延參數等于1的情況。而對于非廣延氣體來說,分子間作用力對氣體性質產生影響,使得氣體整體上顯示某種關聯性,分別對應參數大于1時的正向關聯和參數小于1時的逆向關聯。從曲線中可以看到,正向關聯極容易隨著參數增加而加強,隨著自由程的縮短,氣體的流體性質逐漸喪失,系統整體上會出現某種相變過程。需要注意的是,非廣延參數以零為下限,看似是強制要求,其實不然,這實際是熵增加原理的直接體現[20]。

4 結論

本文基于非廣延統計理論,計算了非廣延氣體的雙粒子分布函數和相對速度分布函數,并由此計算了碰撞頻率。然后根據單粒子分布函數得到了非廣延氣體平均速率的表達式,并根據該結果得到了相應的平均自由程的公式。通過數值計算發現,碰撞頻率比隨著非廣延參數靠近9/7逐漸趨于無窮大,同時平均自由程逐漸趨于零,這顯示了非廣延氣體的正向強關聯性。此外,當非廣延參數趨于零時,碰撞頻率比明顯下降,平均自由程則明顯有所增加,這顯示了氣體的逆向關聯性。

碰撞頻率和平均自由程的計算結果對于研究非廣延氣體中的輸運性質是非常有用的。比如,根據本文的計算結果,應用初級氣體動理論方法[23]可以很容易給出粘滯系數、熱傳導系數和擴散系數的表達式。