基于全閉環控制技術的滾珠絲桿伺服系統研究*

霍曉銳,趙現朝,石繼超,黃孟杰

(上海交通大學 機械與動力工程學院,上海 200240)

0 引 言

滾珠絲桿機構是數控加工設備中的常用機構,除了可以應用在進給平臺的運動外,還可應用于各種并聯機構和混聯機構的運動支鏈當中。

目前,為了保證運動支鏈的運動精度,高端機床通常采用的是以光柵尺作為位置反饋元件的全閉環的控制策略。這種方式雖然能夠直接測量執行機構的位置,避免由于機械間隙等帶來的穩態誤差;但是由于從電機的輸出端到執行機構之間引入了更多的摩擦和機械間隙等非線性因素,系統的動態特性變差。

全閉環系統中存在最突出的兩個問題是:(1)由于摩擦導致的爬行現象;(2)由于機械間隙在反向運動時產生的平頂現象,需要設計相應的模塊進行補償。基于摩擦模型的補償方式是目前常用的摩擦補償方式之一[1]。這種補償方式的關鍵在于摩擦模型的選擇以及摩擦參數的確定。早期的摩擦模型主要集中在靜態摩擦模型,包括Coulomb模型[2]、Bingham模型[3]以及Stribeck模型[4]等。這類模型雖然能夠比較精確地描述速度穩態時的摩擦力變化,但卻無法描述預滑移階段的動態特性。

直至近幾十年,動態摩擦模型的出現使得系統在低速、小位移狀態下的摩擦力可以得到較為精確的描述,比較著名的模型有Dahl模型[5]、Leuven模型[6]以及LuGre模型[7]等等。其中,Lugre模型憑借其模型簡單、描述精確[8]等特點得到了廣泛的應用。而采用LuGre模型的難點在于4個靜態參數以及兩個動態參數的確定。粒子群算法是確定系統摩擦參數的常用方法之一,該方法的原理簡單、易于實現,但是傳統粒子群算法容易陷入局部極值[9],精度很難提升。

目前,針對機械間隙的補償研究主要停留在系統精度的補償上。對于全閉環系統,系統精度可以通過光柵尺的直接測量得到保證。但是由于間隙的存在,系統在反向運動時會產生短暫的電機轉動,而負載位置不變的現象,這種現象在位置-時間圖中體現為折返處的“平頂”,影響了運動機構的位置響應特性。

本文以數控機床中的滾珠絲桿伺服系統為研究對象,針對LuGre模型,提出一種改進的混沌粒子群算法進行參數辨識,提升辨識精度;并針對摩擦與機械間隙這兩個全閉環控制中的非線性問題,提出一種基于摩擦補償和折返速度補償的混合控制策略;最后通過實驗來驗證該控制方法的有效性。

1 基于LuGre模型的摩擦補償

1.1 系統摩擦建模

滾珠絲桿傳動機構具有剛度大、精度高、可靠性強等特點,一直被用作數控系統中旋轉運動轉化為直線運動的解決方案。

滾珠絲桿傳動系統的機構簡圖如圖1所示。

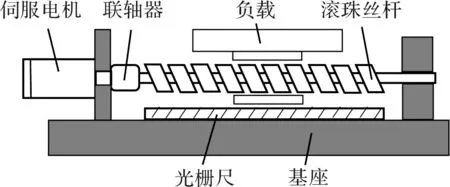
圖1 滾珠絲桿傳動系統

分析傳動系統可知,系統的摩擦主要來源于4個方面:絲桿兩端軸承內部的摩擦、絲桿負載與絲桿之間的摩擦、絲桿負載與導軌之間的摩擦、伺服電機內部的摩擦。這4種產生摩擦的要素中,絲桿負載與導軌之間的摩擦以及伺服電機內部的摩擦所占的比重較大,尤其是在負載加大時,由于工作臺與導軌之間的預緊力加大,此時摩擦力對系統的影響會進一步增大。

本文中采用LuGre模型對系統中的摩擦進行描述,該模型能夠較全面地描述摩擦的動靜態特性,其數學表達式為:

(1)

式中:z(t)—接觸面鬃毛的平均彈性形變量;ω(t)—輸出軸角速度;σ0—鬃毛剛度系數;g(ω)—有界正函數;Tc—庫倫摩擦力矩;Ts—最大靜摩擦力矩;ωs—Stribeck角速度;Tf—總摩擦力矩;σ1—微觀阻尼系數;σ2—粘滯摩擦系數。

在上述表達式中,σ0,Tc,Ts,ωs稱為靜態參數;σ1,σ2稱為動態參數。可以看出,LuGre摩擦模型是一組相對復雜的帶有微分方程的非線性函數,按照傳統方法所確定的評價函數容易存在多個局部極值點,為摩擦參數的精確辨識帶來困難。本文提出一種改進混沌粒子群算法(improved chaos particle swarm optimization, ICPSO),可以有效地避免陷入局部極值,并提升其辨識的精度。

1.2 改進混沌粒子群算法

混沌變量指的是由確定性的方程得出的具有隨機性運動狀態的變量。Logistic方程就是一個典型的,可以通過初始值迭代出混沌序列的方程:

zn+1=μzn(1-zn),n=0,1,2,…

(2)

式中：μ—控制參量,0<μ≤4；zn—混沌序列的第n項。

一旦控制參量μ的大小確定,由任意初值z0∈[0,1],可以迭代出混沌序列z1,z2,z3,…。混沌序列是一串同時具有隨機性和遍歷性[10，11]的序列。

隨機性指混沌序列中的混沌變量有類似于隨機變量的雜亂特性;遍歷性指混沌序列可以不重復地遍歷空間中的所有狀態。而混沌優化[12,13]就是利用了混沌序列的遍歷性,可以將粒子從理論上投放到搜尋空間的任意位置,增強粒子的隨機性,實現全局最優。

粒子群算法(particle swarm optimization,PSO)由Kennedy和Eberhart于1995年提出[14],具有簡單易行、收斂速度快、設置參數少等優點。首先筆者假設一個由N個粒子組成的群體,其中,第i個粒子的位置坐標為xi=(xi1,xi2,…,xin),n—解空間的維數。粒子群中每一個粒子的位置坐標都表示了一組潛在的參數解。將xi代入優化目標函數J(x)中就可以得到第i個粒子的適應度J(xi)。通過比較各個粒子的適應度大小就可以確定出當前粒子群經歷過的最好位置gb=(g1,g2,…,gn),以及各個粒子所經歷過的最好位置pbi=(pi1,pi2,…,pin),i=1,2,…,N。

傳統粒子群算法的迭代公式如下:

(3)

(4)

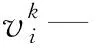
但是傳統的PSO算法無法解決早熟收斂與收斂精度之間的矛盾。

迭代公式中的慣性權重值w具有以下特點:大慣性權重值有利于粒子脫離局部極值,小慣性權重值有利于粒子收斂,提升精度[15]。

本文采用分階段的方式,將粒子群算法的整個迭代過程分為3個階段:

(1)設定慣性權重w的取值范圍[wmin,wmax]。在迭代的第一階段,采用大慣性權重wmax使粒子能夠以較大概率擺脫局部極值;

(2)計算每一步的慣性權重值。其公式如下:

(5)

式中:iter1,iter2—第一、二階段的總步數;iter—當前步數。

與此同時,筆者監測此時粒子群體的收斂情況,如判斷出粒子早熟,則隨機選取部分粒子進行混沌尋優;

(3)采用小慣性權重wmin提升粒子的收斂程度和結果的精確度。

混沌尋優的詳細過程如下:

(1)確定適應度不變的最大代數count,在迭代過程中記錄粒子群的群體最佳適應度J(gb)連續不變的代數;

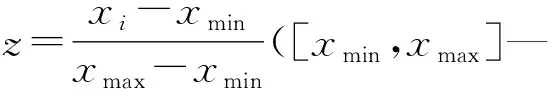
ICPSO算法流程如圖2所示。

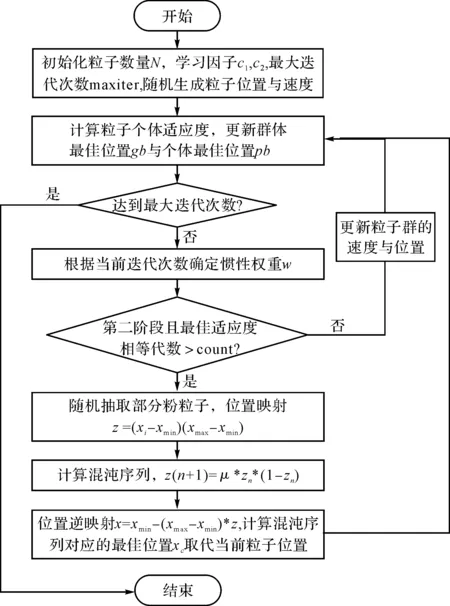
圖2 ICPSO算法流程圖

1.3 摩擦參數辨識方法

摩擦參數的辨識可以分為靜態參數辨識和動態參數辨識兩個部分。靜態參數辨識需要系統的速度達到穩態,根據依次遞增的系統速度及對應的摩擦力矩可以得到Stribeck曲線。

此時,LuGre模型退化為Stribeck模型,即:

(6)

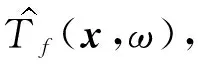
當系統處于低速非穩態時,動態參數成為決定系統摩擦力特性的主導因素[16]。因此,動態參數的辨識需要在系統小位移、低速度的條件下進行。

由于微觀下的剛毛變形量無法測得,本文將系統的微小位移s(t)合理近似成剛毛變形量,角速度取轉角的差分,此時LuGre模型簡化成以下形式:

(7)

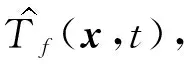
1.4 摩擦參數辨識仿真

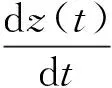
據此,在MATLAB/Simulink下搭建的仿真模型如圖3所示。

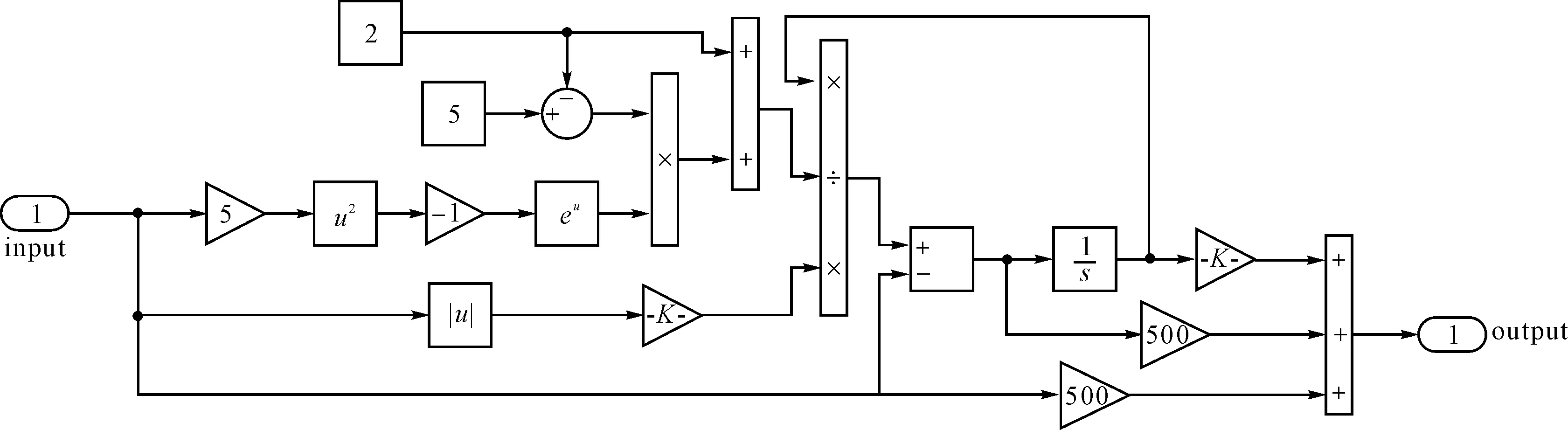
圖3 參數辨識仿真模型

該模型以系統角速度為輸入,摩擦力矩為輸出。在圖3所示的仿真模型中,為方便進行后續的參數辨識仿真實驗,摩擦參數以常量形式進行了人為設定,具體設定參數如下:Ts=5 N·m，Tc=2 N·m，ωs=0.2 rad·s-1，σ0=50 000 N·m·rad-1，σ1=500 N·m·s·rad-1，σ2=0.5 N·m·s·rad-1。

在MATLAB/Simulink中,筆者對圖3所示仿真模型的輸入端施加不同的角速度,具體為:從0.02 rad/s開始,以0.02 rad/s為間隔依次遞增至2 rad/s。在每一個不同的角速度輸入下,讓系統仿真計算10 s的時間,使輸出摩擦力矩達到穩態,記錄不同輸入角速度下的穩態摩擦力矩大小。

根據輸入角速度與輸出摩擦力矩可以繪制Stribeck曲線,如圖4所示(負速度部分完全對稱,此處略去)。

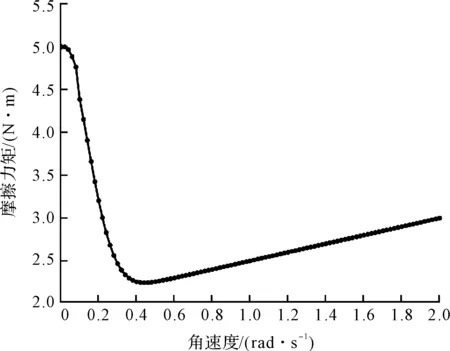
圖4 Stribeck曲線

在靜態參數辨識中,將穩態角速度從0.02 rad/s,以0.02 rad/s為間隔依次遞增至2 rad/s,并同時測出穩態輸出力矩,得到100個原始數據點,然后,先對所得數據的正斜率部分以及負斜率部分進行線性擬合,可以確定出靜態參數的估計值,以此為搜索中心可以使粒子群算法的結果更為精確。

在動態參數辨識中,以s(t)=0.1×10-4sin(0.001t)作為系統的角度輸入,以s(t)的導數作為系統的角速度輸入,持續仿真10 s,將所得結果作為原始數據。

之后,筆者分別采用未優化的普通PSO算法以及ICPSO算法分別進行辨識實驗。

實驗過程中,統一設定最大迭代次數為300,自我學習因子c1=2,群體學習因子c2=2,粒子群數量為100進行實驗。每種算法分別進行獨立重復實驗100次,取100次實驗的平均值作為各自的最終結果。

實驗結果如表1所示。

表1 參數辨識仿真實驗結果

從表1數據可得:相對于PSO算法,ICPSO算法對于Ts，Tc，ωs，σ0，σ1，σ26個摩擦參數的辨識精度均有所提升。

各項參數絕對誤差下降的比例如表2所示。

表2 參數辨識絕對誤差下降比例

從表2數據計算可知:與PSO算法相比,利用ICPSO算法進行摩擦參數辨識,可以使絕對誤差平均下降42.6%。

2 全閉環控制策略

2.1 反向運動間隙

機械結構之間存在的運動間隙會導致全閉環系統的運動特性變差,其中,最明顯的特征就是系統在反向運動時為克服間隙產生的“平頂”現象。

令伺服電機以正弦形式運動,采集電機編碼器的位置信息可以得到半閉環的位移圖像,采集光柵尺讀取到的位移信息可得到全閉環的位移圖像,將兩者同時做出,得到雙位置環位移圖像,如圖5所示。

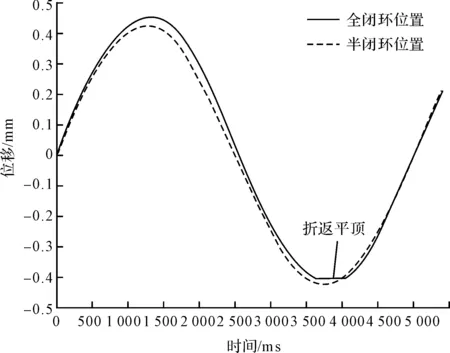
圖5 雙位置環正弦位移圖像

從圖5中可以看出:在光柵尺反饋的全閉環位移信息中,每當系統運動方向變化時,都會出現一小段位移不變的折返平頂;

在此期間,雖然電機角度仍在變化,但是光柵尺顯示的位置信息始終不變。產生這種現象的原因有兩個:(1)光柵尺的精度有限,在折返時由于系統的速率很小,所以會產生短暫的平頂;(2)全閉環系統引入了更多的機械間隙,每當系統運動的方向改變時都需要花費額外的時間度過間隙,從而影響了動態特性。

2.2 全閉環混合控制策略

針對全閉環控制中面臨的摩擦與間隙等非線性因素,本文提出一種基于前饋摩擦補償模塊、折返速度補償模塊以及PID控制器的混合控制策略。

其中,折返速度補償模塊的原理如下:在伺服系統運行時,在主機程序中設計一個標志位,記錄系統運動的方向;當判斷出位置指令會使系統運動的方向發生改變時,為電機目標速度增加一個常量ΔV;與此同時,監測伺服系統中光柵尺的讀數情況,如果脈沖數為0,則在下一個控制周期繼續增加ΔV,否則,停止間隙速度補償。

利用該策略可以縮短系統間隙的過渡時間,增強系統位置跟隨的動態精度。

全閉環混合控制策略的控制框圖如圖6所示。

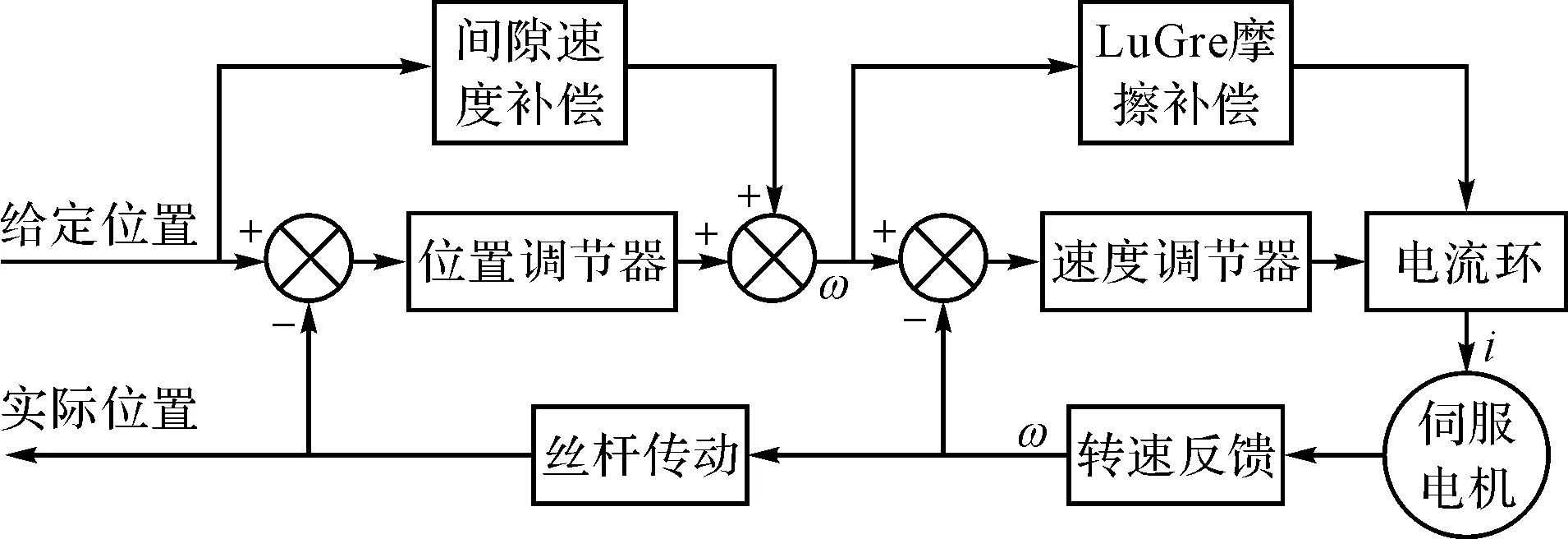
圖6 全閉環混合控制策略

3 實驗驗證

3.1 實驗平臺

該伺服控制系統基于倍福公司的TwinCAT3平臺。控制主站采用Windows10系統計算機,控制從站包含EtherCAT端子模塊(EK1100、EL5151)以及copley電機驅動器。

硬件選型:絲桿導軌行程800 mm,絲桿直徑16 mm,導程5 mm;直流伺服電機額定電壓24 V,空載最高轉速2 000 r/min,最大扭矩0.32 N·m,電機前端裝有減速器,減速比9 ∶1;相對式光柵尺有效行程920 mm,分辨率5 μm;負載塊質量7.5 kg。

該實驗采用的控制時鐘周期為250 μs,可以滿足對系統狀態的實時反饋。實驗過程中,采用TwinCAT3的Scope View模塊實現對于光柵尺位移、伺服電機轉速以及目標控制量等實驗數據的實時采集。

該實驗平臺的硬件組成部分如圖7所示。

圖7 實驗平臺

3.2 摩擦補償實驗

采用摩擦補償主要是可以保證電機在負載情況下的轉速特性。此處首先進行靜態參數的辨識:令電機以ω=0.01+k·0.002 rad/s恒速運轉,k=200為采樣點數;同時,記錄對應摩擦力矩的大小;之后采用ICPSO算法對摩擦參數進行擬合計算,最終獲得系統靜態參數的辨識結果,如表3所示。

表3 靜態參數辨識結果

在動態參數辨識過程中,為了使系統能夠以足夠小的位移運動,筆者采用電機的轉矩控制模式;在獲得了預位移量、摩擦力矩值后,通過ICPSO算法擬合參數得到的結果,如表4所示。

表4 動態參數辨識結果

之后,筆者通過辨識所得的摩擦參數,設計摩擦補償模塊。

為驗證摩擦補償的效果,此處令電機跟隨ω=3.14sin(0.6πt) rad/s的速度曲線,分別在施加與不施加摩擦補償的情況下運動,得到的未摩擦補償的速度跟隨結果,如圖8所示。

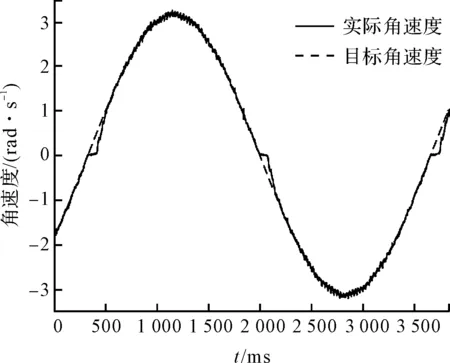
圖8 未摩擦補償的速度跟隨

摩擦補償后的速度跟隨結果如圖9所示。

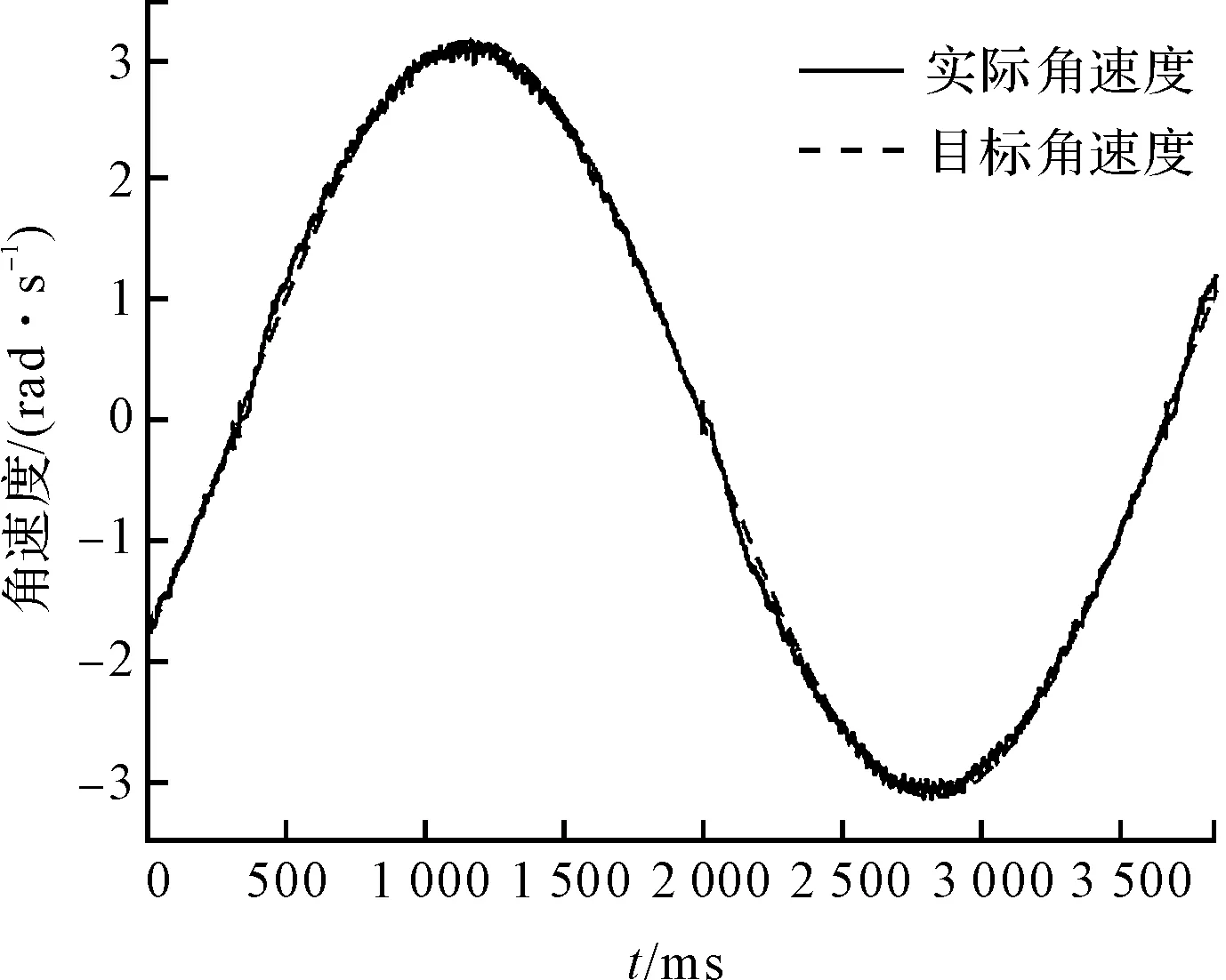
圖9 摩擦補償后的速度跟隨

從圖(8,9)中可以看出:在摩擦補償之前,電機的速度跟隨存在明顯的低速死區現象存在;在摩擦補償之后,這種現象得到明顯改善。

摩擦補償前,電機的速度跟隨誤差情況如圖10所示。

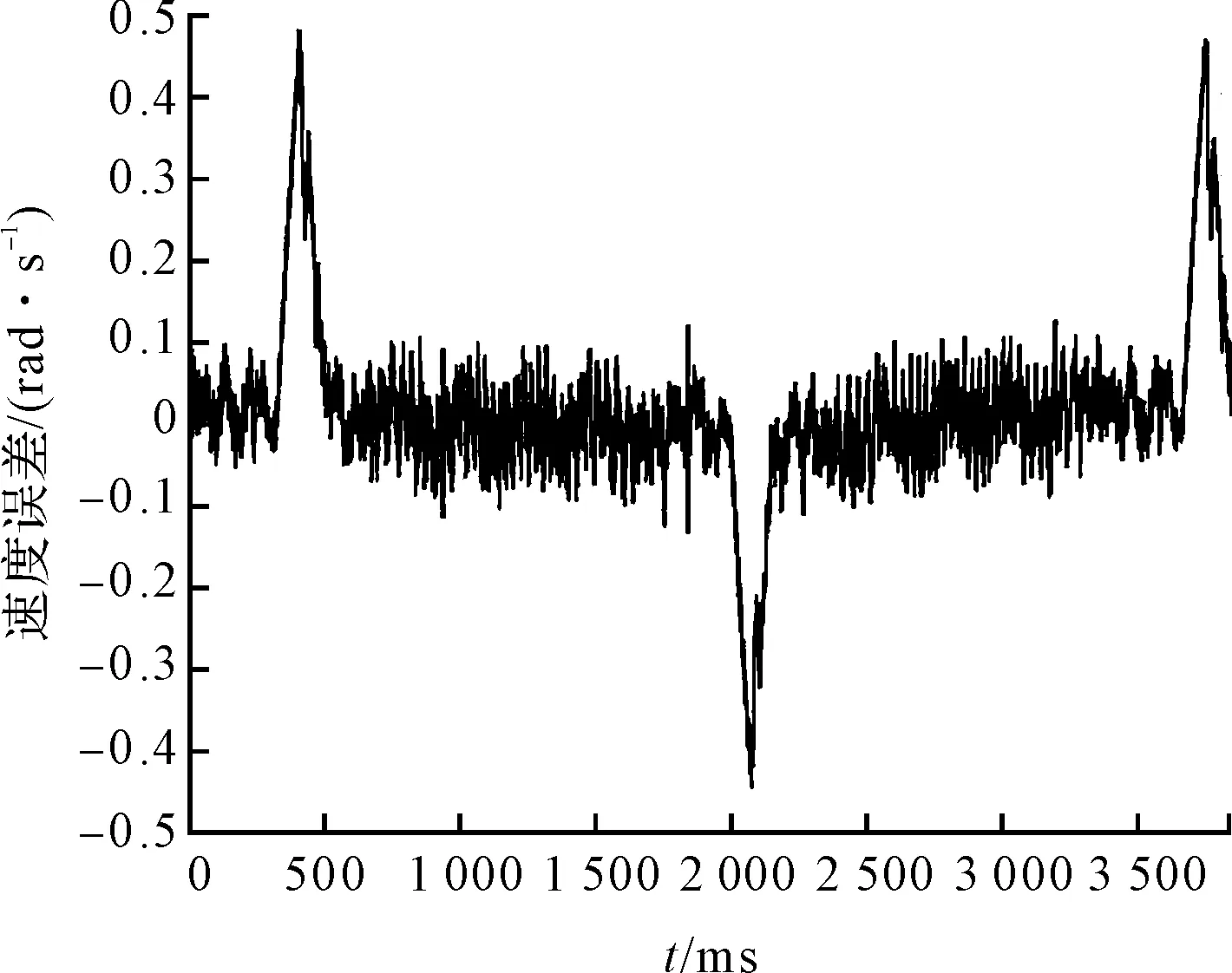
圖10 補償前速度跟隨誤差

摩擦補償后,電機的速度跟隨誤差情況如圖11所示。

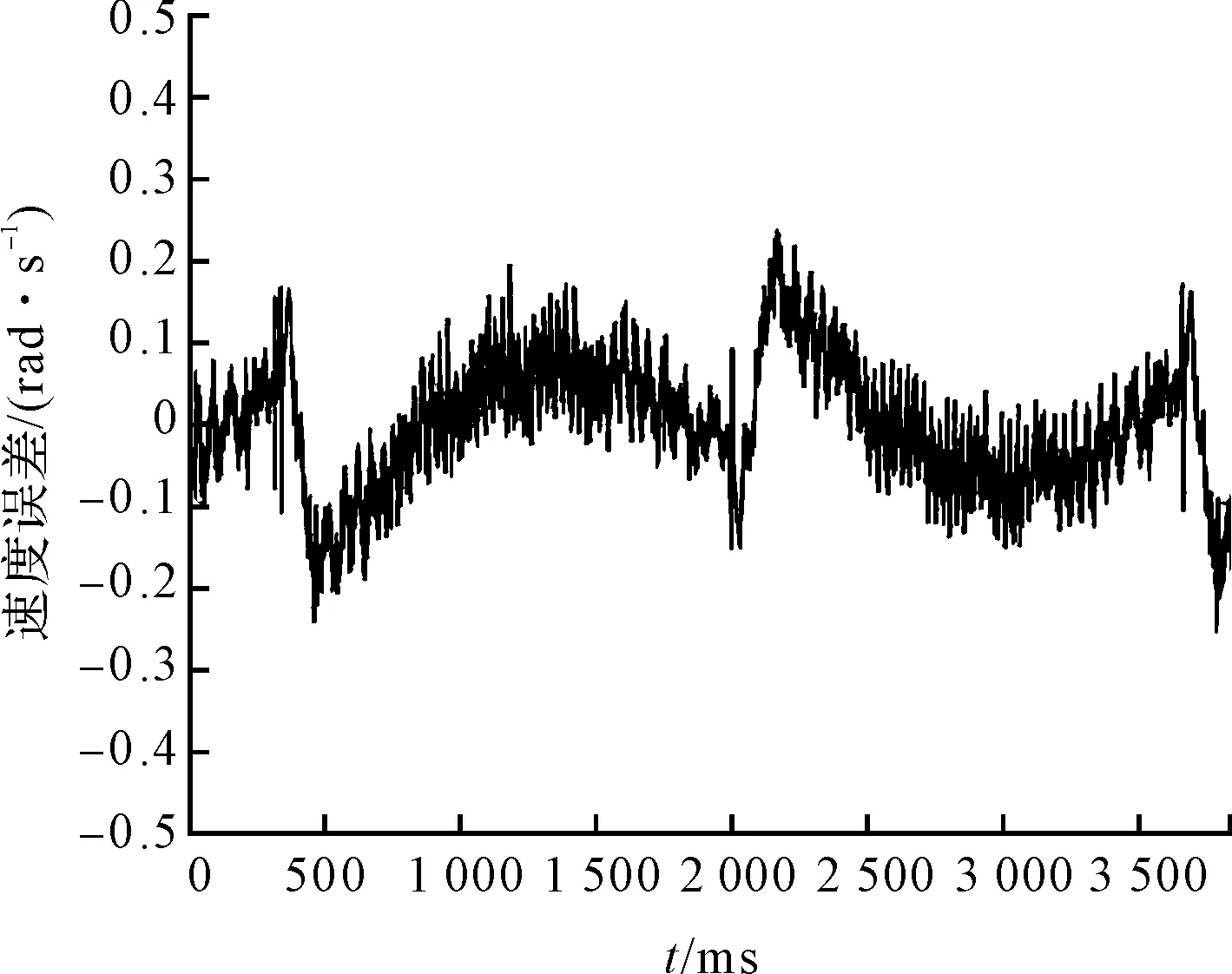
圖11 補償后速度跟隨誤差

根據圖(10,11),并經計算可得,摩擦補償前伺服系統的速度跟隨的最大誤差為0.476 9 rad/s,平均誤差為1.2×10-2rad/s;補償后最大誤差為0.235 9 rad/s,平均誤差為1.9×10-3rad/s。由此可見,補償后伺服系統速度跟隨的最大誤差降低了50.53%,平均誤差降低了84.17%。

3.3 位置跟隨實驗

此處,令系統跟隨以x=0.8sin(0.4πt) mm的位移規律運動,分別在普通PID控制器與混合控制策略下運動,得到的PID控制位移跟隨曲線如圖12所示。

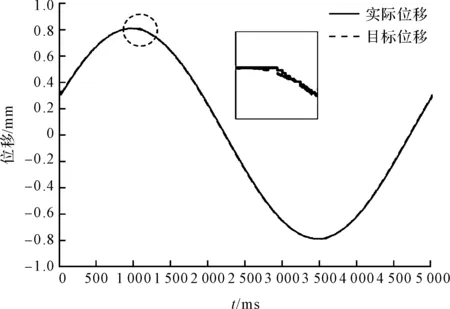
圖12 PID控制位移跟隨曲線

得到的混合策略位移跟隨曲線如圖13所示。

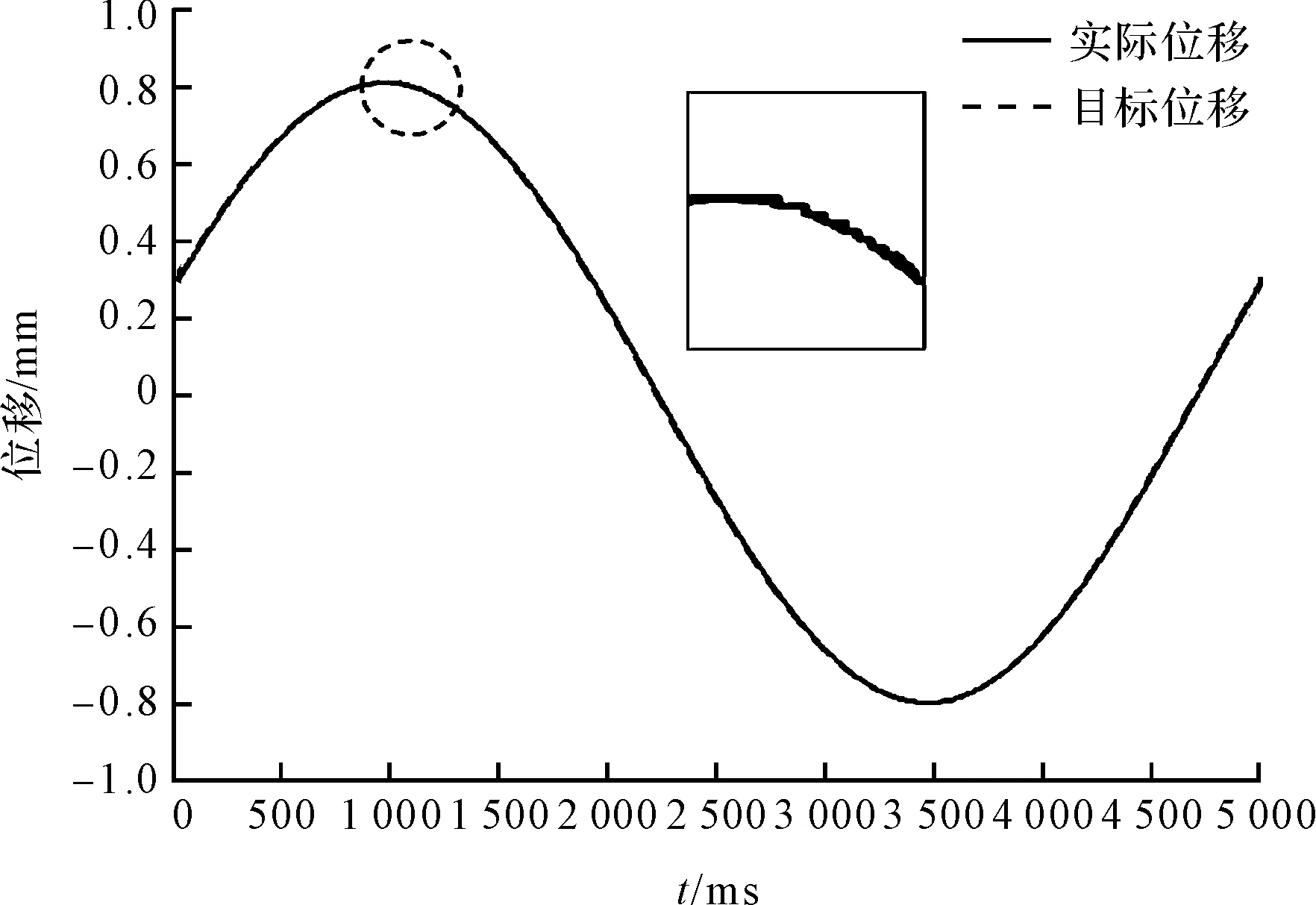
圖13 混合策略位移跟隨曲線

從圖(12,13)中的細節可以看出:采用混合策略的全閉環伺服系統可以有效降低折返處的位置誤差。

采用PID控制的位置跟蹤誤差如圖14所示。

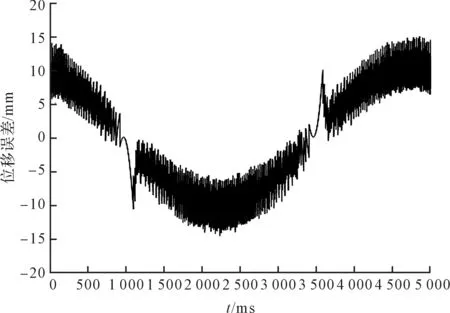
圖14 PID控制位置誤差

采用混合控制策略的位置跟蹤誤差如圖15所示。

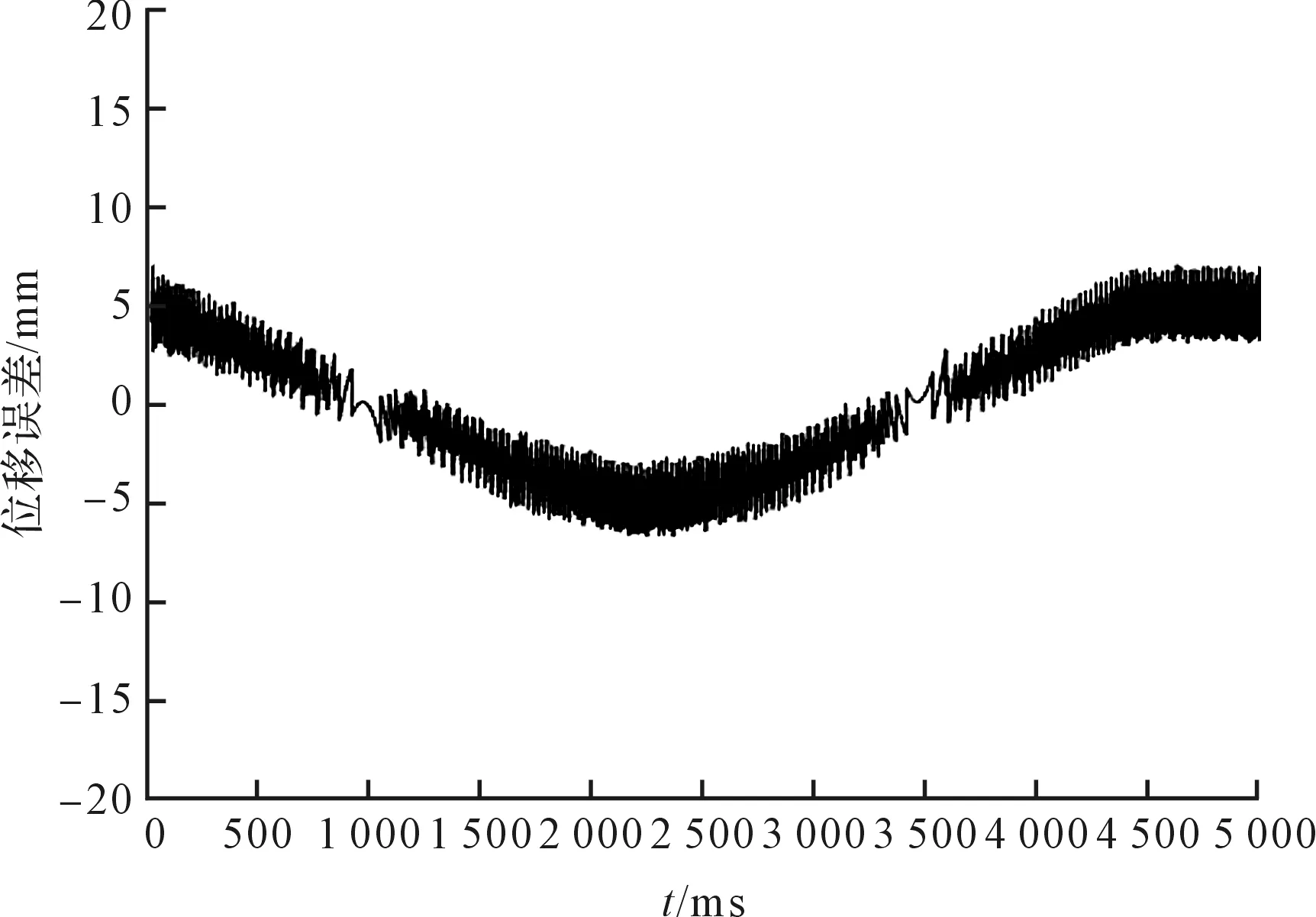
圖15 混合控制位置誤差

根據圖(14,15),并經計算可得,采用PID控制的位置跟蹤誤差最大為14.91 μm,平均跟蹤誤差為6.81 μm;而采用混合控制策略的位置跟蹤最大誤差為11.77 μm,平均跟蹤誤差為5.11 μm,并且沒有誤差突變現象產生。

4 結束語

本文提出了一種改進的混沌粒子群算法,提升了摩擦參數辨識精度;針對滾珠絲桿全閉環伺服系統,設計了一種混合控制策略,提升了系統的動態響應。通過仿真與實驗的研究得出以下結論:

(1)在仿真實驗條件下,改進的混沌粒子群算法相比于常規的粒子群算法精度更高,使參數辨識的絕對誤差平均下降42.6%;

(2)針對本文搭建的滾珠絲桿全閉環伺服系統,采用改進的混沌粒子群算法進行參數辨識的摩擦補償可以有效消除全閉環系統的低速死區,使系統的速度跟隨精度提升50%以上;

(3)基于前饋摩擦補償和反向速度補償的混合控制策略,可以有效降低系統由于反向運動造成的位置跟隨誤差。

在后續的研究工作中,筆者將針對不同工況下的有間隙的位置伺服系統,采用混合控制策略展開實驗探究,并對不同系統的參數取值方法進行深入研究。