一種提高非完整小圓弧曲率半徑參數(shù)評價精度的方法*
羅智孫,吳國新*,何小妹,何學軍,朱春梅
(1.北京信息科技大學 現(xiàn)代測控技術教育部重點實驗室,北京 100192;2.中國航空工業(yè)集團 北京長城計量測試技術研究所,北京 100095)
0 引 言
非完整小圓弧指的是圓弧輪廓對應中心角度小于120°的、曲率半徑范圍為0~25 mm的弧線或弧面[1]。非完整小圓弧輪廓性能特殊,在國防科技工業(yè)和精密制造業(yè)中得到了廣泛應用,例如:航空發(fā)動機葉片的前后緣輪廓對發(fā)動機的氣動性能和葉片的疲勞性能產(chǎn)生直接影響;數(shù)控機床刀具的刀尖部分直接決定其加工精度;一些精密零部件的邊緣倒角用于去除加工毛刺,改善零部件應力集中的情況。
曲率半徑參數(shù)作為小圓弧輪廓的核心參數(shù),其精度對工件的生產(chǎn)制造性能極為重要,存在精確測量及評定的迫切需要[2]。然而,其非完整性和圓弧半徑范圍小的特點導致測量及評價難度大,因此,對曲率半徑參數(shù)估計的準確性一直存在著爭議。
通過已有文獻對非完整小圓弧評價方法的研究,基本確定了影響曲率半徑評價結果的主要圓弧參數(shù),以及各參數(shù)對評價過程影響的大致趨勢[3]。影響評價精度的主要圓弧參數(shù)有圓弧的理論半徑、圓弧輪廓點集所對中心角,以及圓弧輪廓點集的輪廓度誤差[4]。在通常情況下,圓弧的理論半徑越小,評價的難度及誤差就越大;圓弧輪廓所對中心角度越小,曲率半徑評價的準確性也越差;輪廓點集的輪廓度誤差越大,評價精度也隨之下降[5]。
在上述3個影響因素中,圓弧半徑是要求取的目標值,無法對其進行調(diào)節(jié)。因此,學者們普遍從圓弧輪廓點集所對中心角,以及圓弧輪廓點集的輪廓度誤差上著手,通過減小輪廓度誤差的影響或者增大中心角度的方法,以此來提高其評價的精度。
GUEVARA I等[6]提出了一種基于平均絕對誤差來擬合一組點的魯棒幾何方法,該方法通過最小化到數(shù)據(jù)點的幾何距離之和,基于梯度或二階導數(shù)的快速迭代算法,以左、右導數(shù)確定迭代新方向,將數(shù)據(jù)點擬合成圓弧,繼而求取半徑;該算法在計算效率上可作為常規(guī)算法的替代方法,原理上降低了輪廓度誤差對評價過程的影響,增強了算法的魯棒性,使其對異常值和數(shù)據(jù)噪聲不敏感,進而提升了評價精度。FEI Zhi-gen等[7]從非完整小圓弧所對中心角度著手,采用了一種基于徑向基函數(shù)神經(jīng)網(wǎng)絡(RBFNN)的雙向預測方法,將觀測數(shù)據(jù)視為時間序列,并對其進行了雙向延伸,再進行了插值,通過增大圓弧長度進而增大圓弧輪廓所對中心角度,經(jīng)過大量數(shù)據(jù)的訓練學習,最終證實該方法擬合的穩(wěn)定性和準確性遠勝于預測之前。
在一些特定領域及工況條件下,以上方法具有很好的應用效果,但都具有一定的局限性。如基于徑向基函數(shù)神經(jīng)網(wǎng)絡(RBFNN)的雙向預測法,所需圓弧輪廓數(shù)據(jù)樣本量巨大,實際工程中可供用于訓練學習的圓弧數(shù)據(jù)樣本數(shù)量基本難以達到要求,其應用的普適性不高。不過,此種試圖在一定時間跨度內(nèi)通過預測延長圓弧長度的方法亦是一種可行手段。
基于這種啟發(fā),筆者提出一種基于自適應三次指數(shù)平滑預測模型的方法,對已有的圓弧輪廓數(shù)據(jù)點集進行預測延伸,針對傳統(tǒng)三次指數(shù)平滑預測中平滑系數(shù)難以確定的問題,在其基礎上添加自適應算法,進行優(yōu)化。
1 小圓弧輪廓所對中心角對曲率半徑參數(shù)評價的影響
非完整小圓弧曲率半徑參數(shù)評價的難點之一在于其非完整性,即輪廓中心角占總圓或球面的比例[8]。圓弧輪廓所對中心角度越小,說明這段圓弧的完整性也越差;完整性差意味著該段圓弧所缺失的信息較多[9],直接導致擬合過程中的不確定因素增多。
因此,在完整性較差的圓弧的擬合過程中,不僅采用不同擬合方法情況下擬合的結果相差很大;采用同種方法對同一圓弧數(shù)據(jù)擬合,每次的擬合結果也不盡相同。非完整小圓弧曲率半徑參數(shù)評價的難點主要在于擬合的穩(wěn)定性及重復性差,直接導致曲率半徑估計的準確性也存在爭議。
在利用某光學三坐標測量儀測量一件圓心角為10°左右的非完整小圓弧標準件時,經(jīng)處理后得到輪廓數(shù)據(jù)點集,再使用測量儀自帶軟件將其擬合成圓;由于圓弧數(shù)據(jù)所對中心角過小,缺失信息太多,每次擬合圓的圓心位置與曲率半徑參數(shù)的結果差異性很大,重復性比較差,難以判定哪次擬合的結果才是準確的。
其擬合效果如圖1所示。
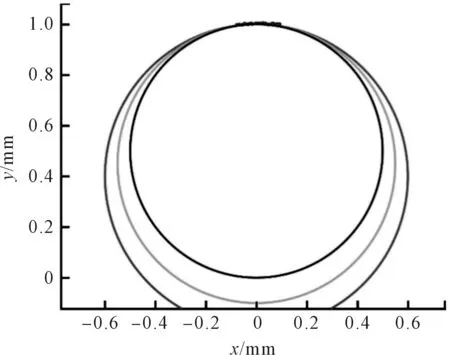
圖1 非完整小圓弧曲率半徑評價的難點
在非完整圓弧的擬合評價過程中,影響圓弧輪廓數(shù)據(jù)的曲率半徑參數(shù)評價精度的因素有:理論半徑R、輪廓所對中心角θ和輪廓度誤差f等。
為了能對輪廓中心角參數(shù)進行更準確地分析,在仿真分析過程中,需控制其他的影響因素不變,即在對一組小圓弧輪廓數(shù)據(jù)點集進行分析時,應保持半徑與輪廓度誤差不發(fā)生改變,調(diào)整中心角度慢慢增大,觀察圓弧輪廓數(shù)據(jù)點集所對應中心角度對曲率半徑參數(shù)評價結果的影響趨勢。
筆者采用3組理論半徑分別為0.05 mm,1 mm以及25 mm的圓弧數(shù)據(jù)點集,輪廓度誤差均為理論半徑值的14%左右,使用最小二乘法擬合,得出不同半徑的小圓弧輪廓數(shù)據(jù)的評價誤差隨中心角度增大的變化趨勢,如圖2所示。
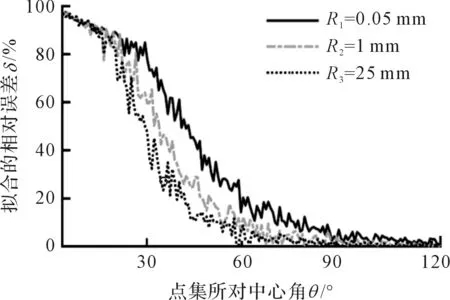
圖2 小圓弧中心角度對評價影響的趨勢圖
由圖2可知:在非完整圓弧的評價過程中,不同半徑圓弧數(shù)據(jù)的評價誤差變化趨勢基本一致,都隨著輪廓所對中心角度的增大而減小,評價誤差的變化率均呈現(xiàn)出先增大再減小的趨勢;
當圓弧中心輪廓角度小于10°或者大于60°時,曲線較平穩(wěn),通過增大中心角減小評價誤差的方法效果不太明顯;反觀約15°~60°之間的圓弧,隨著中心角度的增大,誤差曲線下降的速率快,評價精度提升的效果最為明顯。
基于以上仿真分析的結果可知:針對輪廓中心角為60°以下的非完整小圓弧曲率半徑參數(shù)評價上的難點,可利用一種增大圓弧所對中心角度的方法,來降低曲率半徑參數(shù)評價過程中的誤差。
在所有能增加圓弧長度的方法中,時間序列預測法作為一種常用外延方法而被廣泛應用[10]。
2 三次指數(shù)平滑法的預測模型
時間序列預測就是通過分析其歷史數(shù)據(jù)的規(guī)律性,來研究其未來的變化趨勢。一般來說,歷史數(shù)據(jù)對未來值的影響是隨時間間隔的增長而遞減的,所以,更切合實際的方法是對各期數(shù)據(jù)進行加權平均求取預測值[11]。
簡單加權平均法用的是算術平均數(shù),近期數(shù)據(jù)的權值比遠期數(shù)據(jù)的權值大,即越近的數(shù)據(jù)對預測值的影響越大[12]。
指數(shù)平滑法是一種特殊的加權平均法,其原理是將權值按照指數(shù)遞減的規(guī)律分配。根據(jù)平滑的次數(shù)不同,分為一次指數(shù)平滑法、二次指數(shù)平滑法和三次指數(shù)平滑法;每個算法都是在之前的算法基礎上再進行一次平滑運算處理得到的。一次指數(shù)平滑法適用于無趨勢效應、平滑序列的預測;二次指數(shù)平滑法適用于線性時間序列數(shù)據(jù)的預測;三次指數(shù)平滑法適用于非線性變化、規(guī)律性較差的數(shù)據(jù)[13]。
在本文的研究中,筆者將圓弧輪廓數(shù)據(jù)點集根據(jù)其空間位置順序視為時間序列,其大體趨勢呈線性變化。但從精密測量的角度分析,由于圓弧表面粗糙度及測量過程中存在誤差,實測數(shù)據(jù)點的規(guī)律性并不高,采用三次指數(shù)平滑法預測的精度更高。
筆者將實際測量所得的小圓弧輪廓數(shù)據(jù)點集按照空間坐標位置排序,并將序數(shù)視為時間序列的期數(shù),對之進行三次指數(shù)平滑。其數(shù)學模型如下:
已知圓弧采樣點坐標點集X=[x1,x2,x3,…,xn],Y=[y1,y2,y3,…,y…n],三次指數(shù)平滑預測模型為:
(1)

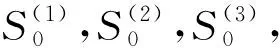
(2)
同理,對Y進行三次指數(shù)平滑處理。
利用式(2)可求得:
(3)
at2,bt2,ct2的求解同理。
將求出的at1,bt1,ct1和at2,bt2,ct2代入式(1)中,設定好預測的期數(shù)m,即可得到后期的預測值。
在三次平滑過程中,為增強預測的準確性,各個參數(shù)的選取需要依照一定的要求。接下來對主要參數(shù)及其選取標準分別進行分析。
2.1 平滑初值的選取
在平滑過程中,若歷史數(shù)據(jù)樣本較小,初始值對預測值影響較大,則取前3或前5組數(shù)據(jù)的算術平均值為平滑的初值;若樣本量大,初始值對預測值影響較小,則取第一組數(shù)據(jù)作為平滑初值[14]。
2.2 平滑系數(shù)的選取
在指數(shù)平滑過程中,選擇合適的平滑系數(shù)α是提高預測精度的關鍵[15]。α值越大,加權系數(shù)序列的衰減速度越快,所以α值實際起著控制參加平均的歷史數(shù)據(jù)對預測值影響的作用,α值愈大意味著歷史數(shù)據(jù)對預測值影響越強。
在平滑系數(shù)選取過程中往往遵循以下準則:
(1)若序列的基本趨勢較平穩(wěn),預測偏差由隨機因素造成,則α應取小一些,以減小修正幅度,使預測模型能包含更多歷史數(shù)據(jù)的信息[16];
(2)若預測目標的基本趨勢已經(jīng)發(fā)生系統(tǒng)的變化,則α應取大一些,以偏重新數(shù)據(jù)對原模型進行大幅度修正,使預測模型適應預測新目標的變化[17]。
在實際應用中,α的取值范圍一般在0.1~0.3為宜。
2.3 預測步數(shù)的選取
在三次指數(shù)平滑預測過程中,可采用一步預測或者多步預測,一步預測即是固定式(1)中的m值為1,每次預測只得到一個預測點,預測后將該預測點并入點集重新進行下一期數(shù)據(jù)的預測;多步預測的m不為1,即可通過一次預測獲得多期的預測點。
在兩種預測方案的選擇上,多步預測雖然能減少迭代計算的次數(shù),提升計算效率,但是由于預測的過程中對于趨勢變化的反應速度不如一步預測,導致后期預測數(shù)據(jù)的準確性不如前期預測數(shù)據(jù);隨著預測期數(shù)增加,誤差累加導致后期預測點容易產(chǎn)生偏離,無法進行長期的精確預測[18]。
而用一步預測時,每預測一期數(shù)據(jù)后便將該數(shù)據(jù)納入數(shù)據(jù)點集,雖然迭代次數(shù)增多,計算時間更長,但一定程度上減緩了誤差累積的速率,使預測點在多次預測后依然保持較高的準確性,能夠?qū)A弧外延的角度進一步增大,對于曲率半徑評價精度提高更有幫助。
因此,在精度要求較高的小圓弧輪廓數(shù)據(jù)的預測上,一步預測的性能上要優(yōu)于多步預測。
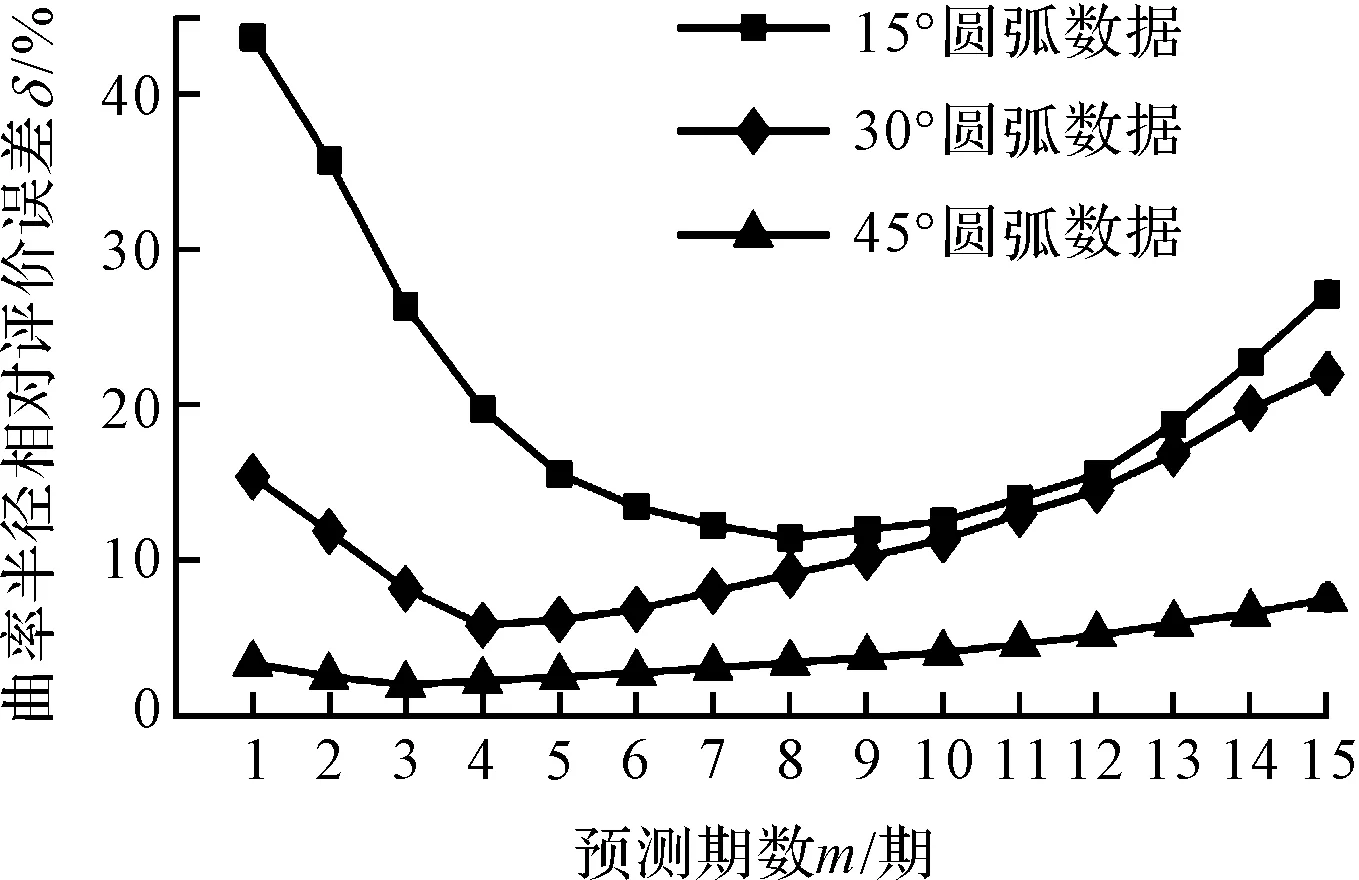
此處筆者采用三次指數(shù)平滑預測模型,對一組輪廓對應中心角為15°左右的圓弧數(shù)據(jù)點集進行預測,其結果如圖3所示。
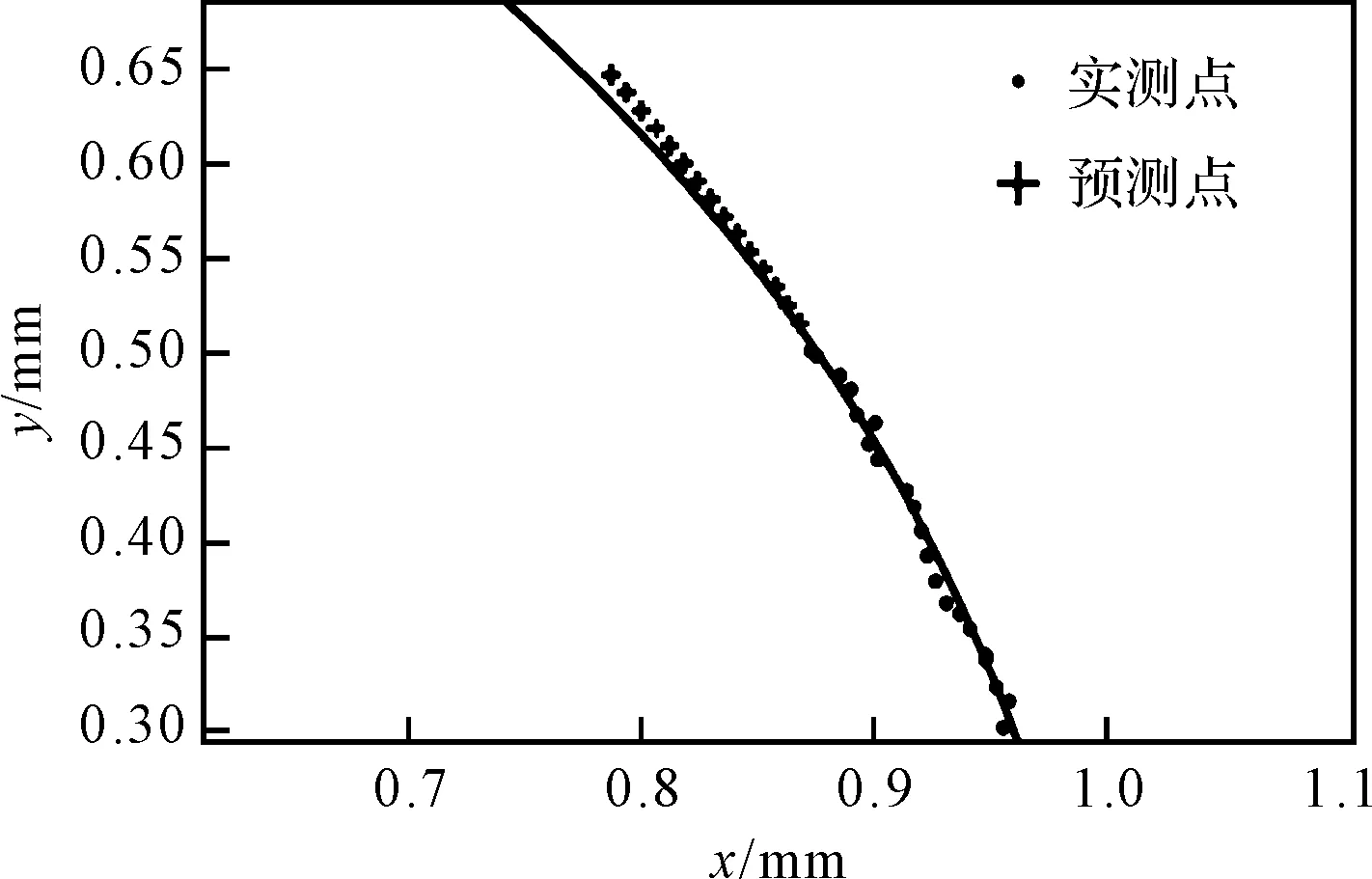
圖3 三次指數(shù)平滑預測發(fā)散圖像
由圖3可知:對比使用Hough變換法擬合的該組數(shù)據(jù)的圓弧曲線,可觀察到雖然前期的預測點具備一定準確度;但隨著預測期數(shù)的增加,后期的預測點相對于擬合的標準圓弧發(fā)生了較明顯的偏移,并且偏移量逐漸增大。
在對圖3進行分析時,將預測點出現(xiàn)偏離的原因鎖定在平滑系數(shù)的確定上,僅憑借實際運用經(jīng)驗確定的平滑系數(shù)顯然具有一定的局限性;并且,由于每次迭代計算后都會將預測點并入點集,使得預測的樣本量逐漸增大,預測趨勢發(fā)生細微改變,平滑系數(shù)卻依然是第一次預測前使用的值。
因此,針對如何提高預測結果準確性的問題,最佳平滑系數(shù)的確定策略亟待優(yōu)化。
3 自適應三次指數(shù)平滑預測模型
在三次指數(shù)平滑的過程中,平滑系數(shù)的選取常常帶有較強的主觀性,由于沒有實際值與預測值比較,無法確定其是否為最優(yōu)系數(shù)。
另外,在傳統(tǒng)三次指數(shù)平滑模型中,平滑系數(shù)一旦確定便無法再進行調(diào)整,對于樣本環(huán)境波動的適應能力差,僅適用于一次預測。當一次預測結束后,新產(chǎn)生的預測點再并入數(shù)據(jù)點集中進行下一輪預測,樣本的數(shù)量發(fā)生改變,再使用該平滑系數(shù)進行計算就可能不太適用了。
并且,由于實測數(shù)據(jù)點集數(shù)量過大,預測一個點需要點集所有的點都代入進行迭代計算,增加了許多不必要的繁瑣計算;根據(jù)時間序列預測的原理,越是靠前的歷史數(shù)據(jù)對預測值的影響越小,遠期數(shù)據(jù)的影響幾乎可以忽略不計。
為解決以上兩個問題,筆者提出了自適應三次指數(shù)平滑預測模型,即在原來傳統(tǒng)三次指數(shù)模型的基礎上添加自適應算法進行優(yōu)化。
自適應三次指數(shù)平滑預測模型并不是像傳統(tǒng)的三次指數(shù)平滑法一樣,將所有點全部代入直接預測,而是根據(jù)現(xiàn)有的數(shù)據(jù)點集,從第一期數(shù)據(jù)開始,只截取其中部分點進行三次指數(shù)平滑;計算出這一期的預測數(shù)據(jù)后,就往后移動一步計算,每次移動都將最先一期的數(shù)據(jù)剔除,并加入后一期實測數(shù)據(jù)。
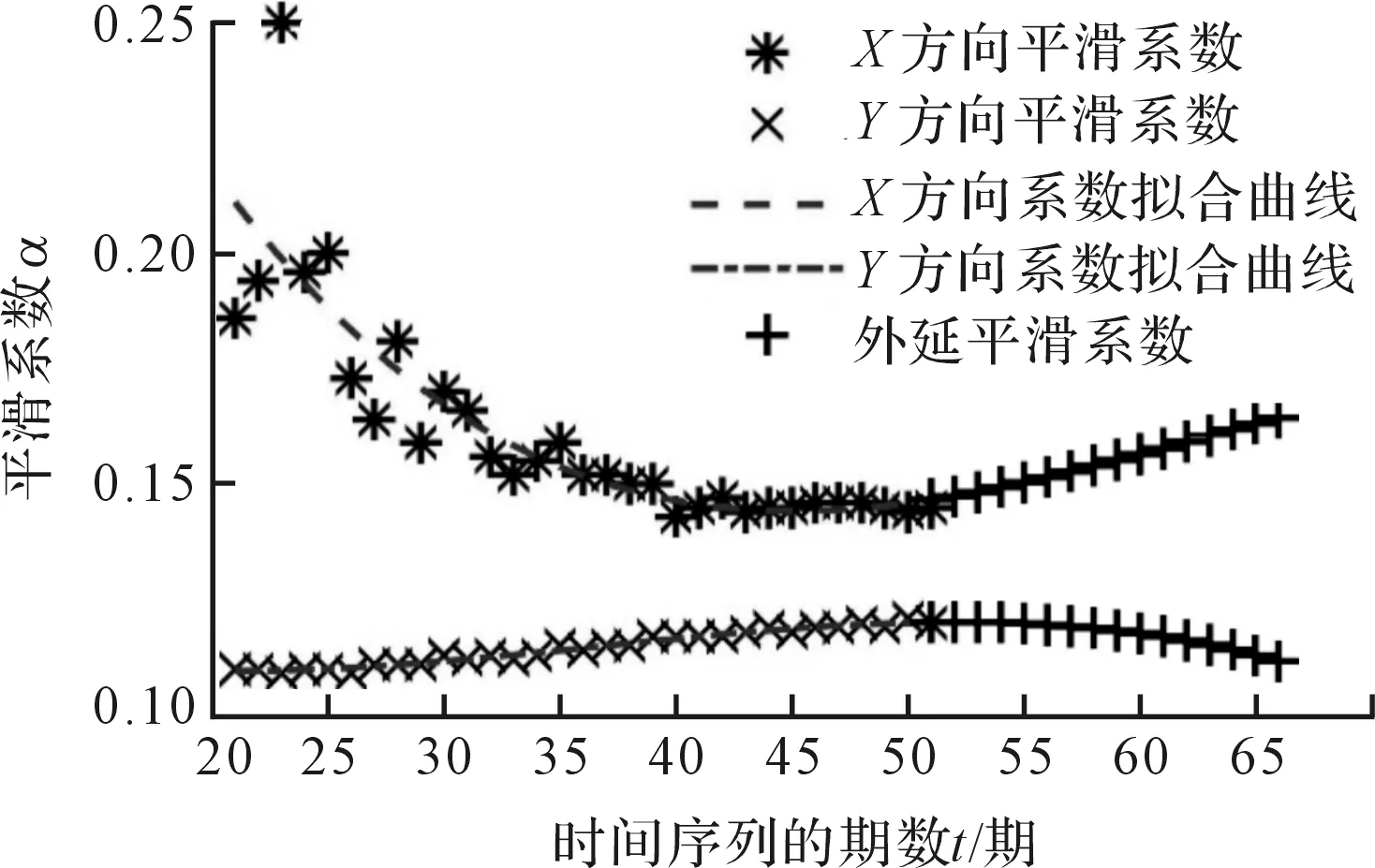
同時,遍歷平滑系數(shù)α的取值空間,進行定步距計算,得出一系列預測點,將所有預測點與當期的實測點進行比較,根據(jù)誤差平方和最小化原則,得出誤差最小的預測點,反推出預測該點的平滑系數(shù)值,即為實時最佳平滑預測值。
經(jīng)過前期歷史數(shù)據(jù)的訓練,可擬合出平滑系數(shù)α的變化趨勢曲線。在點集外進行預測時,由于缺少實測值的比較,則需要根據(jù)α的擬合曲線方程計算后期平滑系數(shù)值,直接利用該平滑系數(shù)參與計算預測實測數(shù)據(jù)點集外的數(shù)據(jù)點。
自適應三次指數(shù)平滑算法流程如下:
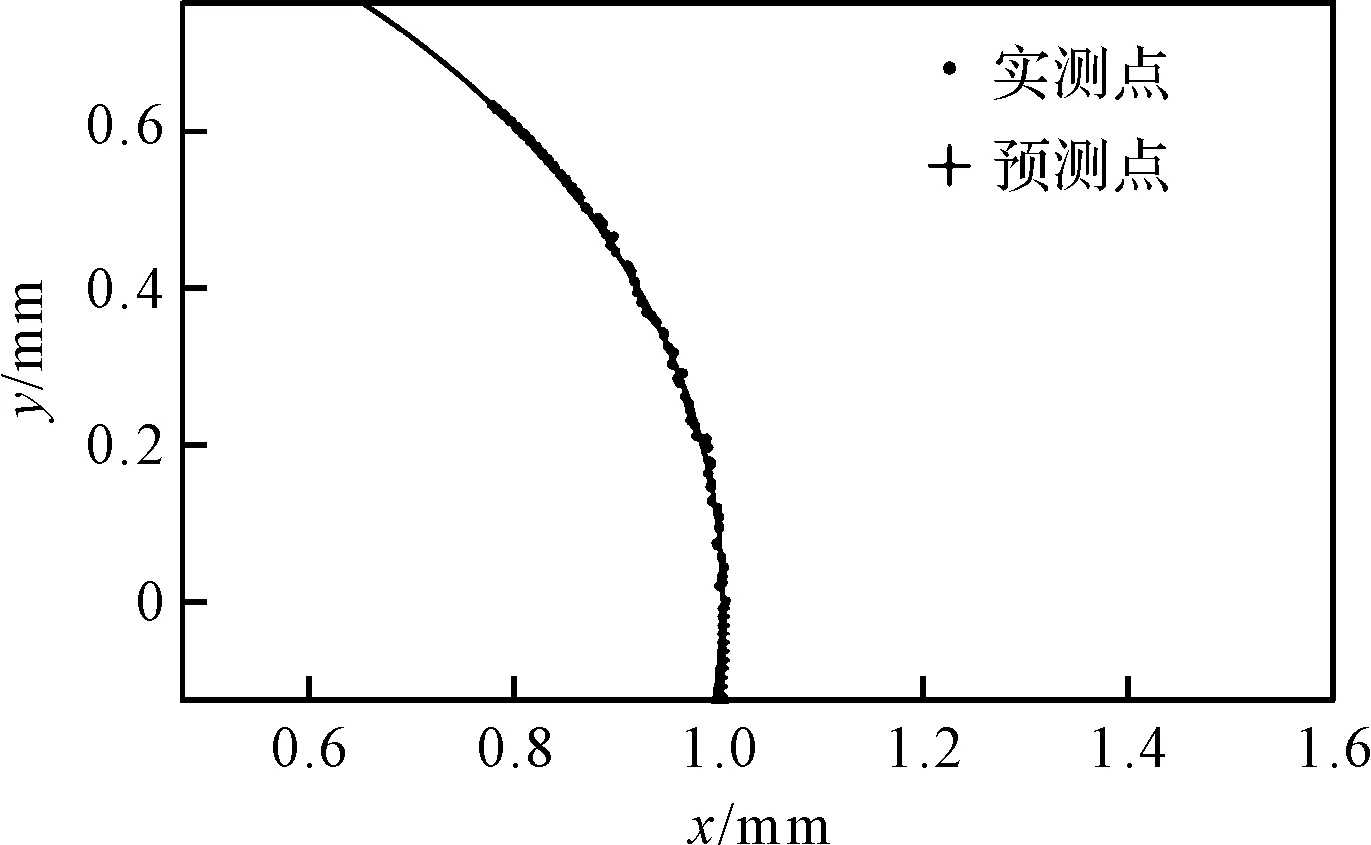
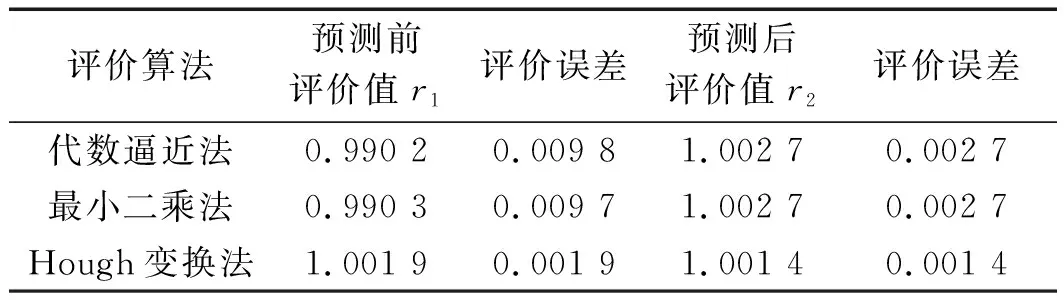
(1)利用現(xiàn)有實測數(shù)據(jù)橫縱坐標點集X和Y,實測樣本點個數(shù)為n,假定每次預測固定采用k期(k (2)去掉第1期數(shù)據(jù),采用第2期至第k+1期實測數(shù)據(jù),重復(1)中步驟,得到最佳平滑系數(shù)α2,以此類推,總共能得到n-k個α值; (3)使用MATLAB的polyfit函數(shù),將α1到αn-k擬合,得到擬合曲線與擬合公式,計算αn-k+1,αn-k+2,…αn-k+m(其中:m—數(shù)據(jù)點集外預測的期數(shù)); (4)當計算移動至使用第n-k期到第n期數(shù)據(jù)計算第n+1期預測數(shù)據(jù)時,將平滑系數(shù)αn-k+1代入進行(2)中三次指數(shù)平滑預測,每次預測后均將預測點并入點集,并剔除最早一期的數(shù)據(jù);以此類推,使用第n+m-k-1期到n+m-1期數(shù)據(jù),代入αn-k+m計算第n+m期預測值; (5)將數(shù)據(jù)點集按逆序排列,即第1期數(shù)據(jù)變?yōu)榈趎期,第n期變?yōu)榈?期,重復步驟(1)~(4); (6)將原數(shù)據(jù)點集與預測數(shù)據(jù)點集合并形成新數(shù)據(jù)點集,利用評價方法進行曲率參數(shù)評價。 自適應三次指數(shù)平滑法固定樣本移動計算示意圖如圖4所示。 圖4 自適應三次指數(shù)平滑固定樣本移動計算示意圖 相比于傳統(tǒng)三次平滑系數(shù)α的確定,自適應三次指數(shù)平滑模型的優(yōu)點在于,能根據(jù)時間序列自身的變化來實時監(jiān)測并調(diào)整α的值,每次迭代過程在取值空間內(nèi)尋找平滑系數(shù)最優(yōu)解;并且在迭代過程中移動計算,固定了時間序列樣本的數(shù)量,規(guī)避了由于預測的樣本量改變而產(chǎn)生的影響,更有助于客觀觀察α的變化趨勢,以及用于后期點集外平滑系數(shù)的確定。 每次用于計算的樣本點數(shù)量k的取值同樣會影響預測的結果。樣本點過多則導致迭代的次數(shù)減少,得到平滑系數(shù)的個數(shù)不夠,不利于其擬合以及觀測其變化趨勢;樣本點過少則容易受輪廓點集數(shù)據(jù)的偶然誤差影響,導致平滑系數(shù)的波動較大,可能出現(xiàn)偏離較大的點,同樣不利于平滑系數(shù)α的擬合。 因此,在每次預測樣本k值的選取上,一般取總數(shù)據(jù)點個數(shù)的40%~50%左右。至于樣本外預測點的個數(shù)m的確定,則需要經(jīng)多次實驗,分析不同圓弧數(shù)據(jù)下預測的最佳期數(shù)。 筆者使用9組理論半徑分別為0.05 mm、1 mm、25 mm,輪廓對應中心角梯度分別為15°、30°和45°的數(shù)據(jù)點集,點集的輪廓度誤差均在理論半徑值的2.6%左右,點集個數(shù)均為50個;利用自適應三次指數(shù)平滑法進行數(shù)據(jù)的雙向預測,再用最小二乘法評價曲率半徑,與直接使用最小二乘法進行比較,分析兩種情況下的曲率半徑評價精度的變化情況。 此法的原理即是利用前期數(shù)據(jù)來分析出平滑系數(shù)的變化趨勢,再通過該趨勢調(diào)整后期平滑系數(shù),利用得到的平滑系數(shù),進行實測輪廓數(shù)據(jù)點集外的數(shù)據(jù)點預測。在前期每一次迭代遍歷搜索最佳平滑系數(shù)的過程中,將步長設定為0.001,α的取值空間為(0,1)。為提高迭代速度,減少不必要的計算,可根據(jù)實際情況縮小α的取值范圍;固定每次用于預測的樣本點個數(shù)k值為20。 因此,在整個移動迭代過程中,由50個實測點集數(shù)據(jù)可得到30個α值,觀察α值的變化趨勢,通過對之擬合得到變化曲線及變化公式,利用變化公式,即可求取后期用于點集外數(shù)據(jù)預測的平滑系數(shù),利用得到的α值,繼續(xù)進行固定樣本數(shù)移動計算,就能到準確的輪廓點集外預測點。 平滑系數(shù)α的變化趨勢及擬合如圖5所示。 圖5 自適應三次指數(shù)平滑系數(shù)擬合圖及后期推導值 在平滑系數(shù)擬合的過程中,筆者使用MATLAB的polyfit函數(shù)對其進行擬合,不同擬合次數(shù)后期的α變化趨勢具有一定差異性。經(jīng)多組數(shù)據(jù)綜合分析可知,在二次擬合、三次擬合和四次擬合中,選擇三次擬合具有更高的擬合優(yōu)度。 使用與圖3中同一組輪廓對應中心角為15°左右的圓弧數(shù)據(jù)點集,筆者進行自適應三次指數(shù)平滑預測。 預測后的擬合結果如圖6所示。 圖6 自適應三次指數(shù)平滑法雙向預測擬合效果圖 由圖6可知:對比圖3中單獨使用三次指數(shù)平滑的預測結果,添加自適應優(yōu)化后預測的誤差明顯減小,大大延緩了誤差累積的速度,使后期預測點相對于理想圓的偏移量減小了許多;預測的角度增大,使圓弧外延的長度得以增加。 筆者采用不同角度的圓弧數(shù)據(jù),進行預測后的誤差比較,其結果如圖7所示。 圖7 不同角度下的預測誤差比較 經(jīng)過以上數(shù)據(jù)的評價分析結果,驗證了自適應三次指數(shù)平滑預測方法應用在非完整小圓弧曲率半徑參數(shù)評價上的可行性。 經(jīng)初步驗證,在使用最小二乘法評價曲率半徑參數(shù)時,使用自適應三次指數(shù)平滑法處理輪廓對應中心角小于60°的圓弧后,具有提高評價精度的作用;并且,隨著預測次數(shù)的增加,評價誤差呈現(xiàn)先減小再增大的趨勢,即存在最佳預測期數(shù)的問題。 經(jīng)過對評價誤差變化趨勢的原因分析可知,短期內(nèi)預測的數(shù)據(jù)比較精準,可提高曲率半徑參數(shù)評價的精度;但隨著預測期數(shù)的增加,中長期預測數(shù)據(jù)的誤差會慢慢增大。 從上述實驗中可觀察到:對于15°的小圓弧,雙向預測的期數(shù)m取8期時最佳,評價的誤差最小;對于30°的小圓弧,預測期數(shù)m取4期時最佳;對于45°的小圓弧,預測期數(shù)m取3期時最佳。用各數(shù)據(jù)點集相鄰兩點的夾角乘以對應最佳期數(shù),可求出各組不同角度圓弧數(shù)據(jù)預測的最佳角度。 經(jīng)計算可知,各組圓弧數(shù)據(jù)預測的最佳角度均在5°左右波動,此時,評價誤差減至最小,對評價精度的提升效果最佳。 在上文中,為方便計算均使用最小二乘進行曲率半徑參數(shù)評價,在不同中心角度輪廓數(shù)據(jù)下,筆者分析了采用該方法對評價的影響。 為驗證自適應三次指數(shù)平滑法應用的普適性,即在使用其他評價方法時,對非完整小圓弧的評價精度依然具有提高的效果,筆者以一組理論半徑為1 mm,圓心角為30°,輪廓度誤差為0.026 4的數(shù)據(jù)點集為例,并根據(jù)上節(jié)的結果,取預測期數(shù)m為4,對其進行自適應三次平滑處理,再分別使用代數(shù)逼近法、最小二乘法和Hough變換法,評價曲率半徑參數(shù)值;并將其與原來未使用自適應三次指數(shù)平滑處理前的曲率半徑參數(shù)評價結果進行比較,預測前后的評價誤差分析。 不同評價方法在預測前后評價誤差分析如表1所示。 表1 不同評價方法在預測前后評價誤差分析(單位:mm) 經(jīng)過以上不同評價方法下的分析可知,對比使用不同評價方法,自適應三次指數(shù)平滑法預測處理均有不同程度的提高;對于最小二乘法及代數(shù)逼近法這種代數(shù)和最小化原理的參數(shù)評價方法,比之Hough變換法這種參數(shù)空間內(nèi)尋優(yōu)的評價方法,經(jīng)預測后的精度提升效果更明顯。 實驗結果表明:相比于未處理直接評價的方法,使用自適應三次指數(shù)平滑法對圓弧輪廓數(shù)據(jù)進行處理后,再利用評價方法進行曲率半徑評價的方法,曲率半徑的評價精度得到了提升;并且,該方法對于60°以下的非完整小圓弧的評價精度提升效果較為明顯;角度越小,評價精度的提升就越大。 在使用該方法時預測圓弧點集數(shù)據(jù)時,將圓弧對應中心角度增加5°左右最佳,此法對于不同評價方法均能提升評價的精度,具備一定的普適性。 在研究非完整小圓弧曲率半徑參數(shù)評價方法中,筆者基于仿真分析的方法,計算了一定輪廓度誤差下輪廓所對中心角度對評價過程的影響趨勢;然后,根據(jù)仿真結果分析,針對解決60°以下完整性較差的圓弧在曲率半徑參數(shù)的評價上存在的難點,提出了一種基于自適應三次指數(shù)平滑預測模型的方法,增大了圓弧輪廓中心角度,進而提升了曲率半徑參數(shù)評價的精度。 筆者通過采用不同圓弧數(shù)據(jù)進行了多組對照組實驗。實驗及研究結果表明: (1)使用該方法處理60°以下的非完整小圓弧輪廓數(shù)據(jù)點集后,再對數(shù)據(jù)進行評價,評價精度得到了進一步提升。并且,利用此方法將圓弧輪廓增大5°左右,對評價的精度的提升效果最佳; (2)該方法具有一定的普適性,可作為一種前期的數(shù)據(jù)外延方法,配合各種評價方法對小圓弧曲率半徑參數(shù)進行精確評價,為提高非完整小圓弧曲率半徑參數(shù)評價的穩(wěn)定性與準確性提供了一種有效解決方案。 在下一步的研究工作中,筆者將配合各類不同原理評價方法的使用,進一步研究曲率半徑參數(shù)評價精度的具體提升效果及其內(nèi)在聯(lián)系。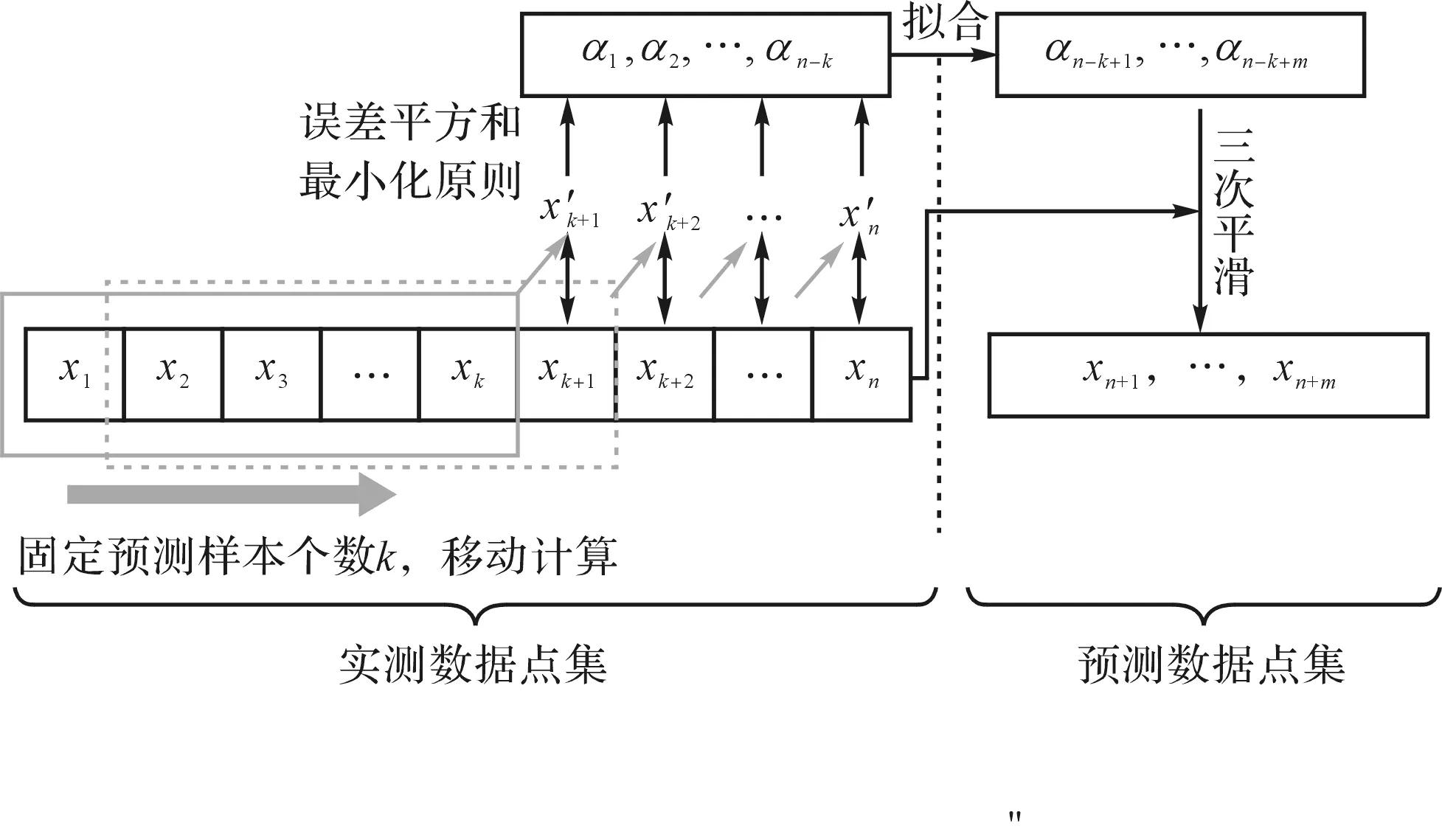
4 實例計算及精度分析
4.1 不同圓弧數(shù)據(jù)預測前后評價結果比較
4.2 不同評價方法預測前后評價結果比較
5 結束語

