圖神經網絡的標簽翻轉對抗攻擊

吳翼騰，劉偉，于洪濤

（信息工程大學，河南 鄭州 450002）

1 引言

對抗攻擊指有目的地對輸入數據施加微小擾動，以使學習模型輸出錯誤的預測結果[1]。本文認為與對抗攻擊直接關聯的研究可上溯至20 世紀70 年代的統計診斷[2]。統計診斷最早研究了學習模型的微小擾動對統計推斷帶來的影響。近年來，隨著深度學習的發展，其應用安全受到廣泛關注。Szegedy等[3]研究圖像數據的卷積神經網絡（CNN,convolutional neural network）安全問題時提出了“對抗樣本”概念[4]。Zügner 等[5]提出處理圖數據的深度學習模型圖神經網絡（GNN,graph neural network）的對抗攻擊。

圖神經網絡對抗攻擊研究正處于快速發展階段，相關研究成果活躍于國際學術會議[6-8]。分析最新研究成果發現，當前研究存在擾動類型不足、前提假設單一等問題。現有研究的擾動類型通常僅考慮增刪節點和連邊；攻擊假設通常僅基于矛盾數據假設，具體說明如下。

1) 擾動類型不足。現有圖神經網絡對抗攻擊的擾動類型[9-10]主要是特征擾動、增刪連邊和節點注入[5,11-13]，沒有考慮將訓練數據中的特定樣本標簽翻轉為其他類別導致模型預測錯誤的標簽翻轉攻擊。標簽翻轉攻擊已被其他數據類型的對抗攻擊場景廣泛研究。例如，統計診斷[2,14]的經典模型均值漂移模型和局部影響分析模型[15-17]都詳細研究了因變量擾動對模型統計推斷的影響，是標簽翻轉攻擊的最初形式。張宏坡等[18]提出了一種基于熵值法的標簽翻轉攻擊方法，來評估樸素貝葉斯分類器對標簽噪聲的穩健性。Mu?oz-González 等[19]實現了針對深度神經網絡的標簽翻轉數據投毒攻擊。文獻[20]針對基于圖的半監督學習模型（區別于圖神經網絡）建立了統一的標簽翻轉攻擊架構。然而，針對圖神經網絡的對抗攻擊還未見標簽翻轉攻擊這種擾動類型。

2) 前提假設單一。現有圖神經網絡對抗攻擊通常僅基于矛盾數據假設建立攻擊模型，而未考慮攻擊前后模型訓練參數的顯著差異以及測試數據和訓練數據分布的一致性。本文基于以下3 種攻擊假設展開研究。①文獻[5,8-9,13,21]將投毒攻擊建模為尋求擾動方法，在訓練集上構建一組存在矛盾的訓練數據，使重訓練的圖神經網絡在訓練集上的損失最大，以降低測試數據預測準確率。本文將現有攻擊方法概括為基于矛盾數據假設的攻擊方法。②矛盾數據假設不能很好地對過擬合攻擊場景建模。本文受統計診斷[2,14,22]研究工作的啟發，引入參數差異假設，即“有效攻擊前后圖神經網絡訓練參數應該具有較大差異”的假設建立攻擊模型。③對抗攻擊方法忽視了機器學習最基本最常見的前提假設——同分布假設，即“隨機劃分的訓練集和測試集應該具有相同分布”的假設。

本文基于3 種攻擊假設分別建立圖神經網絡的標簽翻轉攻擊模型，以期在不同數據分布條件下分析圖神經網絡對標簽噪聲的敏感性和潛在安全漏洞。圖神經網絡應用廣泛，它不僅應用于節點分類、圖分類、鏈路預測等復雜網絡任務，也可應用于文本分類、關系抽取等自然語言處理任務，還可應用于圖像分類、目標檢測等計算機視覺任務。在上述應用中，圖神經網絡的訓練數據通常需要人工收集和標記，實際應用中多采用眾包技術收集和標記數據。該收集和標記方式成本低廉且方便快捷；但無法充分保證標簽質量，進而導致數據中存在不可避免的標簽噪聲，影響圖神經網絡的學習過程[18]，更無法避免精心設計的投毒數據。鑒于此，圖神經網絡標簽翻轉攻擊的研究意義是從攻擊者的角度研究標簽翻轉攻擊，可以預知圖神經網絡在各項任務中的安全威脅，評估圖神經網絡對標簽噪聲的敏感性，為標簽噪聲的檢出和過濾、設計穩健的圖神經網絡提供理論基礎。本文主要工作如下。

1) 針對圖神經網絡對抗攻擊擾動類型不足的問題，提出評估圖神經網絡對標簽噪聲穩健性的標簽翻轉對抗攻擊方法。

2) 針對圖神經網絡對抗攻擊前提假設單一的問題，首先基于經典的矛盾數據假設建立標簽翻轉攻擊模型；然后引入參數差異假設和同分布假設，建立標簽翻轉攻擊模型。

3) 理論分析證明了在一定條件下，基于同分布假設模型的攻擊梯度與基于參數差異假設模型的攻擊梯度相同，從而建立了2 種攻擊方法的等價關系，進一步增強了模型攻擊機理的可解釋性。

4) 實驗對比分析了3 種基本假設對應的損失度量在標簽翻轉攻擊中的優勢和不足；大量實驗驗證了標簽翻轉攻擊模型的有效性。

2 基本概念

圖表示為G(V,E)，其中，V為節點集合，E為連邊集合。設節點數|V|=N，則無權無向圖可用對稱的鄰接矩陣A={0,1}N×N表示，AT=A。圖中每個節點有n維特征向量，節點特征用矩陣X={0,1}N×n表示。文獻[23-25]將圖神經網絡簡化為SGC（simple graph convolution），它具有低通濾波器的作用。本文以SGC 為攻擊和研究對象。SGC 模型的表達式為

其中，Yout為SGC 模型輸出，A為濾波矩陣，X為輸入特征向量，W為參數矩陣。在文獻[25]中，A的形式通常為

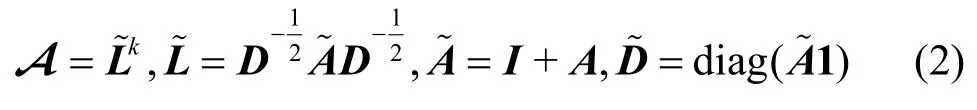
其中，I為單位矩陣，1表示元素全為1 的列向量。設Z=XA，記softmax(·)為σ(·)，Y表示one-hot編碼的標簽矩陣。使用交叉熵損失函數，并將其表達為矩陣形式為

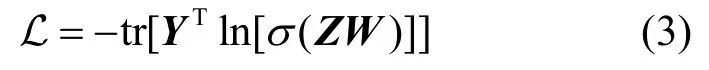
本文研究非指定目標、標簽翻轉的數據投毒攻擊。非指定目標攻擊不指定具體的一個或幾個攻擊目標，需要使測試集整體的預測準確率下降；標簽翻轉攻擊允許將特定的訓練樣本標簽翻轉為其他類別；投毒攻擊允許圖神經網絡對投毒的訓練數據重新訓練，使重訓練的圖神經網絡在測試集的預測準確率下降。

3 標簽翻轉對抗攻擊模型

3.1 基于矛盾數據假設的攻擊模型

文獻[5,8-9,13,21]建立了連邊擾動的圖神經網絡投毒攻擊模型。按上述文獻定義，攻擊方法可以統一概括為以下約束優化問題

其中，A為原始鄰接矩陣，為擾動后的鄰接矩陣，為矩陣中非0 元素的個數，δ為擾動開銷，W*為擾動后得到的訓練參數。投毒攻擊允許對參數重新訓練，是雙層優化問題。

從上述投毒攻擊的統一形式化表述中可以看出，現有攻擊方法都是構造擾動后的樣本數據，使圖神經網絡在擾動后數據集上損失函數達到最大，即圖神經網絡不能很好地擬合擾動后的訓練集，擾動后的訓練集中存在矛盾的訓練數據。根據上述分析，現有方法可概括為基于“有效攻擊的訓練集中存在矛盾的訓練數據”假設（簡稱矛盾數據假設）的攻擊方法。

基于矛盾數據假設，圖神經網絡的標簽翻轉攻擊模型可以表述為以下約束優化問題

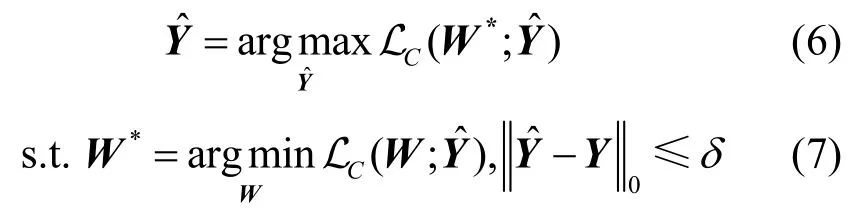
3.2 基于參數差異假設的攻擊模型

受統計診斷學科啟發，基于“有效攻擊前后圖神經網絡模型參數應該具有較大差異”的假設（簡稱參數差異假設），本文建立圖神經網絡的標簽翻轉投毒攻擊模型，可表示為如下約束優化問題

為衡量參數差異，從統計診斷經典文獻[2,14-17,22,26]中引入Cook 距離作為度量攻擊前后的參數差異。

定義1Cook 距離。參數矩陣*W與W0的Cook距離CD 定義為

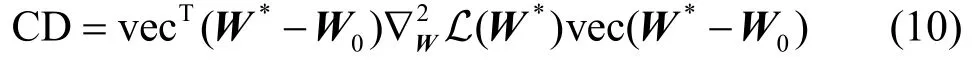
其中，vec(·)表示矩陣按列優先拉直為列向量。

圖神經網絡通過優化求解算法求得使損失函數L 達到最小值的參數矩陣W0，即W0滿足?WL(W0)=0。實用中?WL(W0)≈0。對?WL(W)在W*處進行一階泰勒展開并取W=W0得

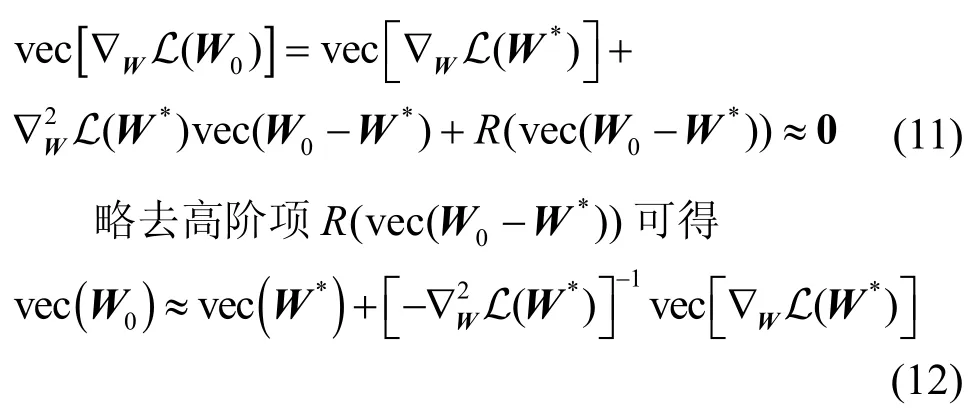
基于以上分析，衡量參數差異的Cook 距離可近似表示為

容易求得

其中，I是與同型的單位陣。此時可逆。基于此，修正后的Cook 距離～CD 表示為

攻擊模型可以表示為

基于參數差異假設的攻擊模型同樣分為投毒攻擊和對抗訓練2 個階段。在式(17)所示的投毒攻擊階段，使用修正后的Cook 距離作為損失函數；在式(18)所示的對抗訓練階段，訓練數據為擾動后的訓練數據，因此與基于矛盾數據假設的損失函數相同。

3.3 基于同分布假設的攻擊模型

圖神經網絡對抗攻擊問題忽略了一種機器學習最基本、最常見的前提假設，即同分布假設。無論圖神經網絡還是其他深度學習或機器學習方法，通常首先基于同分布假設展開研究，即認為訓練集的數據分布與測試集一致，因此這些方法可以在訓練集中學習數據模式，并有效地遷移至測試集。分析實際攻擊場景，投毒攻擊的目的是通過污染訓練數據，使其訓練的圖神經網絡在未污染的測試集上的錯誤率（損失函數）達到最大。若考慮訓練測試集的同分布假設，相應的攻擊模型應該改為通過污染訓練數據，使其訓練的圖神經網絡在未污染的訓練集上的錯誤率（損失函數）達到最大。

根據以上分析，基于“隨機劃分的訓練數據和測試數據對于圖神經網絡模型應該具有同分布性質”的假設（簡稱同分布假設），建立標簽翻轉投毒攻擊模型，可表示為如下約束優化問題

根據3.1 節和3.2 節分析，無論何種攻擊模型，在對抗訓練階段均采用擾動后的訓練數據，因此式(20)與式(7)、式(18)相同。基于同分布假設的攻擊模型在投毒攻擊階段，使用式(3)的交叉熵作為損失函數。從形式上，基于同分布假設的攻擊模型與基于矛盾數據假設的攻擊模型的差異僅體現在損失函數式(6)和式(19)中，式(6)使用擾動后的標簽矩陣，式(19)使用未擾動的標簽矩陣。但二者的建模思想是不同的。本文3.4 節將證明，在某些較弱的條件下，基于同分布假設的攻擊模型與基于參數差異假設的攻擊模型等價。

3.4 攻擊梯度及其等價定理

本節介紹上述攻擊模型的符號記法，主要涉及L、LC、之間的區別。L 由式(3)定義，L 代入的標簽矩陣Y為未擾動的標簽矩陣；LC由式陣；由式(14)定義，為帶有正則項的L。Cook距(6)定義，LC代入的標簽矩陣為擾動后的標簽矩離CD 由式(13)定義；由式(16)定義，表示由～L定義的Cook 距離CD。

設圖神經網絡(1)采用梯度下降法訓練

經過t=t0輪訓練，可得模型的訓練參數。具體地，可求得損失函數對參數的梯度為

代入式(21)，有

對于離散的標簽矩陣Y，優化問題式(6)、式(17)、式(19)屬于NP 難問題。現有文獻主要依據攻擊梯度實施擾動。攻擊梯度是實現有效攻擊的主要依據。

從攻擊梯度的角度，定理1 給出了參數差異假設與同分布假設的等價性。

定理1設

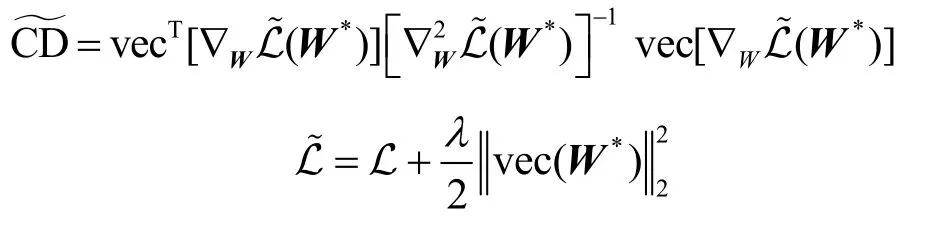
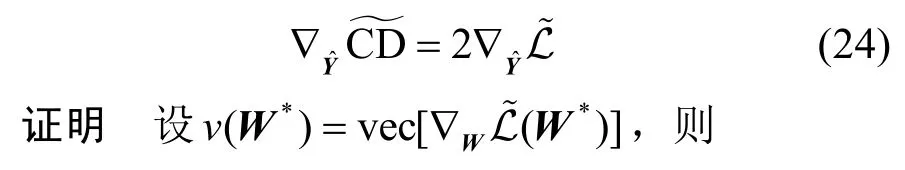
證畢。

定理1 表明，衡量參數差異的Cook 距離的攻擊梯度與基于同分布假設攻擊模型的攻擊梯度相同，因此從攻擊梯度的意義上，上述2 個模型等價。從而說明基于同分布假設的攻擊方法的物理意義也是誘導圖神經網絡訓練出一組異于原始參數的訓練參數。

直接從基于同分布假設的損失函數出發，也可定性分析得出相同的結論：攻擊后式(19)的損失函數L 增大，但攻擊前后損失函數中Y、A、X保持不變，僅參數*W發生改變，表明攻擊前后圖神經網絡的訓練參數具有較大差異。該結論解釋了文獻[13]中提及但未從理論上證明的實驗現象。

矛盾數據假設為

參數差異假設為

同分布假設為

3.5 攻擊算法

根據上述分析，以及式(31)～式(33)求得的攻擊梯度，采用貪心算法實施擾動，可設計圖神經網絡的標簽翻轉對抗攻擊算法如算法1 所示。

算法1標簽翻轉對抗攻擊算法

輸入鄰接矩陣A，特征矩陣X，標簽Y，攻擊點數n

輸出擾動列表disturb_list

4 實驗

4.1 對比實驗

實驗采用型號為TITAN Xp 的GPU 顯卡，運行環境為ubuntu 16.04 系統、cuda10.0、Python3.6 以及Pytorch1.4。實驗采用的數據集為Polblogs[29]、Cora_ml、Cora[30]、Citeseer[31]，數據集的統計特性如表1 所示。由于現有研究尚未考慮標簽翻轉攻擊，將所提3 種標簽翻轉攻擊方法與隨機翻轉標簽攻擊方法Random 以及2 種經典的連邊擾動投毒攻擊方法Mettack[13]和Min-max[32]進行對比實驗。Mettack采用approximating meta-gradients[13]。Min-max 的攻擊方式設置為negative cross-entropy[32]。本文提出的標簽翻轉攻擊方法參數設置與Mettack 保持一致。具體地，對于數據集Polblogs、Cora_ml，圖神經網絡SGC 正向訓練的學習率取α=0.1；對于數據集Cora、Citeseer，學習率取α=0.01。式(2)中SGC 模型冪指數為k=1 和k=2。Mettack 和Min-max 攻擊方法允許對訓練集中連邊總數的5%進行攻擊，并控制擾動后的節點度不超過原始網絡中節點度的最大值；標簽翻轉攻擊方法Random、LC、L 允許對訓練數據中5%的標簽翻轉至其他類別。基于參數差異假設的標簽翻轉攻擊模型正則項λ=0.001。實驗劃分數據集中40%為訓練集，60%為測試集，數據集隨機劃分20 次，記錄20 次SGC初始準確率平均值和攻擊后準確率平均值，實驗結果如表2 所示。表2 中準確率的最小值用黑體標出。

表1 數據集統計特性

表2 準確率

綜合分析以上數據，可以得出如下結論。

1) 考慮標簽翻轉攻擊類型，可以實現有效的投毒攻擊。在相同擾動比例比較基準下，基于3 種假設的標簽翻轉攻擊效果優于基于 Mettack 和Min-max 方法的連邊擾動攻擊效果。實驗結果證明了標簽翻轉這一新的攻擊類型的有效性。

2) 對于標簽翻轉攻擊，隨機翻轉標簽幾乎無法實施有效攻擊。對于5%的擾動，圖神經網絡SGC的預測準確率沒有明顯下降，表明通過式(5)重訓練，圖神經網絡可以抵抗隨機攻擊。而針對本文所提的投毒加擾方式，SGC 的預測準確率下降明顯。這種惡意注入的標簽噪聲可能在數據標記階段產生，圖神經網絡在實用中存在潛在威脅。該標簽噪聲同時具有不易察覺性，將在4.2 節分析。

3) 對于本文提出的3 種標簽翻轉攻擊方法，本文條件下的實驗結果表明，基于參數差異假設和同分布假設的標簽翻轉攻擊模型的攻擊效果優于基于矛盾數據假設的攻擊效果。基于參數差異假設的攻擊效果幾乎與基于同分布假設的攻擊效果相同，與等價性定理得出的理論結果一致。

表2 列出了5%的擾動各攻擊方法的攻擊結果。為進一步比較不同方法的攻擊效果，說明擾動量對攻擊效果的影響，其他實驗條件不變，采用1%～10%的擾動并記錄準確率下降的平均值。選取標簽翻轉攻擊方法Random、LC與L（的實驗結果與L 類似），實驗結果如圖1 所示。

圖1 不同擾動量的攻擊效果對比

總體而言，基于矛盾數據假設和同分布假設的攻擊方法相比于隨機翻轉標簽攻擊有更明顯的攻擊效果。隨機翻轉標簽攻擊無法抵抗圖神經網絡重訓練。無論k=1 和k=2，基于同分布假設的攻擊效果均優于基于矛盾數據假設的攻擊效果，具體原因將在4.3 節詳細分析。實驗結果說明了本文所提出的基于不同假設的標簽翻轉攻擊模型的有效性和攻擊假設的合理性。

4.2 擾動的難以分辨性分析

本節從圖結構統計特征[33]和標簽類別分布兩方面分析標簽翻轉攻擊的難以分辨性。

1) 圖結構統計特征。標簽翻轉攻擊不對圖結構實施擾動，圖結構的各項統計特征例如度分布、節點特征相似度、模體等局部結構特征均保持不變。

2) 標簽類別分布。圖2 繪制了Cora_ml 數據集k=1時原始標簽分布和4種標簽翻轉攻擊方法擾動后的標簽分布（圖2 隨機選取20 次實驗中的某次實驗結果作為示例）。其他數據集的實驗結果與之類似，實驗結論相同。

圖2 標簽類別分布對比

觀察標簽類別分布可知，擾動后各類別標簽分布與原始標簽分布差異不大。若實際場景中需嚴格保持標簽類別分布不變，只需對攻擊算法中的擾動篩選策略稍作調整。例如，不僅依據攻擊梯度大小次序篩選擾動元素，而且限定后一輪攻擊翻轉至前一輪的原始標簽類別。如此迭代，可保持標簽類別分布不變。或者，基于前文實驗證明的隨機翻轉標簽無法實施有效攻擊的結論，為保持標簽類別分布不變，投毒攻擊后再采用隨機擾動平衡標簽分布（簡稱隨機平衡策略）。基于隨機平衡策略，得到Cora_ml 數據集k=1 時基于矛盾數據假設LC和同分布假設L 的實驗結果如圖3 所示（的實驗結果與L 類似）。圖3 中同時對比了4.1 節不使用該策略的實驗結果。可以看出，加入隨機平衡策略的攻擊結果仍然具有可用性，與原攻擊效果差異不明顯。

圖3 加入隨機平衡策略實驗結果對比

4.3 模型的比較分析

本節詳細分析矛盾數據假設、參數差異假設與同分布假設及相應損失函數的合理性，并與隨機翻轉標簽進行對比分析。實驗記錄各方法在擾動量為1%～10%下的訓練準確率和測試準確率；對每種攻擊方法（包括隨機攻擊Random）均同時計算3 種損失函數值，即 LCL（隨機攻擊方法沒有專門的損失函數，只計算隨機擾動后其他3 種損失函數值）。實驗設置與4.1 節相同，所有數值均為20 次實驗的平均值。選取數據集Cora_ml 的實驗結果如表3 和表4 所示。其他數據集和不同參數下的實驗結果與所列結果相似。綜合分析表3 和表4 的數據，可得出以下結論。

表3 k=1 時數據集Cora_ml 基于不同假設的比較分析

表4 k=2 時數據集Cora_ml 基于不同假設的比較分析

1) 基于3 種假設建模的損失函數具有有效性。對于未受擾動的原始數據，4 種攻擊方法對應的基于矛盾數據假設的初始損失函數值和基于同分布假設的初始損失函數值L1、L2、L3、L4相同，當k=1 時，約為77.85；當k=2 時，約為158.60。由于未對數據進行投毒擾動，標簽矩陣Y與相同，且初始參數*W相同，因此損失函數值相同。基于參數差異假設的初始損失函數，當k=1 時，約為102.78；當k=2時，約為181.85。因為基于參數差異假設的損失函數與其他二者相比添加了正則項，導致損失函數的初值不同。基于3 種假設的標簽翻轉攻擊方法均表現出隨著擾動量的增加，訓練測試準確率遞減、損失函數遞增的趨勢，證明了基于3 種假設建立損失函數的有效性。而對于隨機翻轉標簽攻擊方法，隨著擾動量增加，損失函數雖有上升趨勢，但上升并不明顯，盡管擾動量達到10%，依據參數差異或同分布損失L 來衡量，損失函數值也達不到基于3 種假設攻擊方法3%的擾動損失，而擾動后的準確率大致處于基于3 種假設攻擊方法1%擾動量的攻擊效果，隨機翻轉標簽的攻擊效果不理想。

5 結束語

標簽翻轉對抗攻擊在統計診斷、垃圾郵件檢測、圖像中的對抗樣本以及基于圖的半監督學習等領域得到了廣泛研究。本文針對圖神經網絡對抗攻擊擾動類型不足的問題，提出并實現了圖神經網絡的標簽翻轉對抗攻擊。首先，提煉出對抗攻擊有效性機理的矛盾數據假設、參數差異假設和同分布假設。然后，基于3 種假設建立攻擊模型并實驗驗證。有效攻擊的核心是基于攻擊假設建立攻擊模型進而求解攻擊梯度。攻擊梯度是實施有效攻擊的主要依據。為保持標簽擾動的不易察覺性，可增加限制條件保持標簽分布不變，這容易通過修改擾動篩選策略來實現。本文得出以下結論：1) 對于處理圖數據的深度學習模型圖神經網絡，標簽翻轉對抗攻擊具有有效性；2) 采用基于梯度的攻擊方法，參數差異假設與同分布假設建立的攻擊模型等價；3) 本文場景中基于參數差異假設和同分布假設的標簽翻轉攻擊方法優于基于矛盾數據假設的攻擊方法。

由于實際場景中某一樣本難以界定唯一的歸屬類別，或樣本本身存在錯誤標注，這可能大幅降低圖神經網絡模型的預測能力，因此標簽翻轉對抗攻擊研究為圖神經網絡的模型診斷和穩健的圖神經網絡設計提供了必要前提。后續研究工作可基于標簽翻轉攻擊原理，對圖數據中的異常點、強影響點、離群點等進行檢測和模型診斷，從而改善數據質量；并設計圖神經網絡結構，建立能夠防御對抗攻擊干擾的穩健圖神經網絡。