Quantum metrology with coherent superposition of two different coded channels?
Dong Xie(謝東),Chunling Xu(徐春玲),and Anmin Wang(王安民)
1College of Science,Guilin University of Aerospace Technology,Guilin 541004,China
2Department of Modern Physics,University of Science and Technology of China,Hefei 230026,China
Keywords:quantum metrology,quantum switch,quantum Fisher information,coherent superposition
1.Introduction
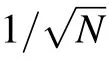
Quantum SWITCH can offer indefinite causal order,which has potential applications in quantum information,such as channel discrimination tasks.[11,12]And quantum switches have also been achieved in photonic systems using superpositions of paths for discrete variables.[13–15]Recently,some works showed that quantum SWITCH can increase the quantum Fisher information.Mukhopadhyay et al.[16]proposed a novel approach to qubit thermometry using a quantum SWITCH and showed that indefinite causal order can be used as a metrological resource.Frey[17]analytically obtained the quantum Fisher information and proved that indefinite causal order can aid quantum depolarizing channel identification.
More importantly,Zhao et al.[18]demonstrated that quantum SWITCH can obtain super-Heisenberg scaling based on the sequential scheme in a continuous variable system.They addressed the comparison with the performances of arbitrary schemes with definite causal order and proved that the optimal scaling is 1/N2.However,up to now,the continuous variable quantum SWITCH has not been realized in experiment.An important question arises:can super-Heisenberg scaling be obtained without quantum SWITCH?
In this work,we investigate the advantage of coherent superposition[19]of two different coded channels in quantum metrology.Without quantum SWITCH,the coherent superposition can also obtain super-Heisenberg scaling based on the sequential scheme in a continuous variable system.We also show that the coherent superposition of two different coded channels can perform better than the quantum SWITCH.
Moreover,we analytically obtain the general form of quantum Fisher information and show that nonlinear Hamitonian can improve the estimation precision and make the measurement uncertainty scale as 1/Nmfor m≥2 based on the sequential scheme.Our results reveal that the coherent superposition and the nonlinearity can provide an important metrological resource,which can be applied to conduct high-precision measurement of coupling strength,the gravitational acceleration and the coefficient from the modification of the canonical commutation relations.
This article is organized as follows.In Section 2,we introduce the scheme of Quantum SWITCH and the corresponding measurement precision.In Section 3,we obtain the estimation precision with the scheme of coherent superposition of two different coded channels.In Section 4,quantum Fisher information with a general nonlinear Hamiltonian is discussed.In Section 5,we discuss about the application in conducting high-precision measurement of coupling strength,the gravitational acceleration and the coefficient from the modification of the canonical commutation relations.We make a brief conclusion and outlook in Section 6.
2.Quantum switch
Unlike classical physics,the order in which quantum physics allows events to occur is indefinite.As shown in Fig.1,based on the sequential scheme,2N black boxes can be accessed,where we consider there are N identical unitary gates U1and U2.The quantum SWITCH generates the controlled unitary gate by querying U1and U2gates N times each,
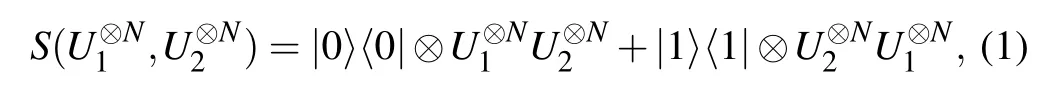
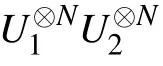
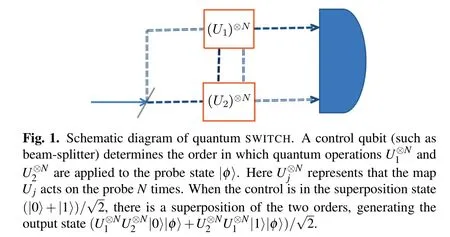
We consider that U1and U2are described by

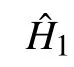
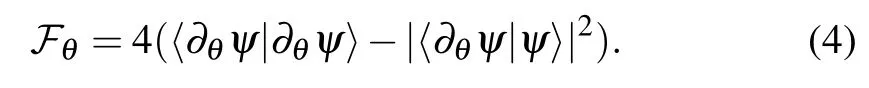
Here,the final output state is
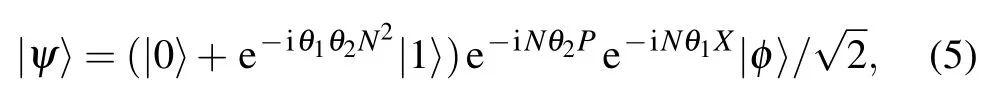
where|φ〉is the initial probe state.Substituting Eq.(5)into Eq.(4),the corresponding quantum Fisher information are achieved
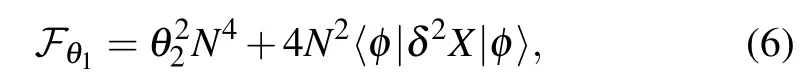
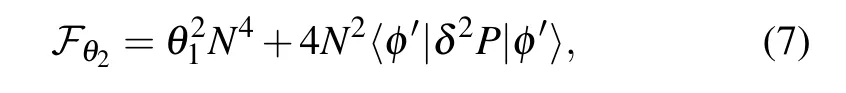
where
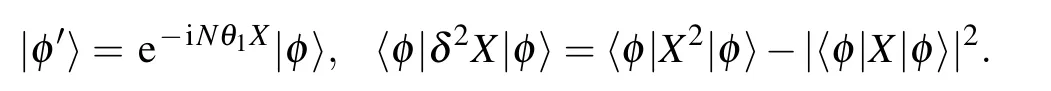
According to the famous Cram′er–Rao bound,[22,23]the estimation precision ofθj(j=1,2)can be given in the largeν limit
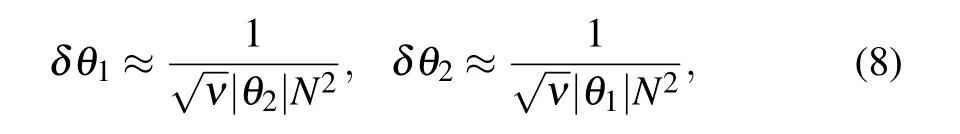
whereνrepresents the total number of experiments,and we consider that Nθ2?〈φ|δ2X|φ〉and Nθ1?〈φ′|δ2P|φ′〉.We can see that super-Heisenberg scaling 1/N2is achieved.This recovers the similar results in Ref.[18].
3.Coherent superposition of two different coded channels
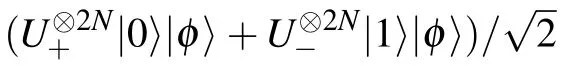
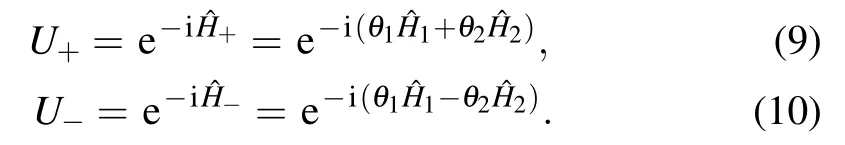
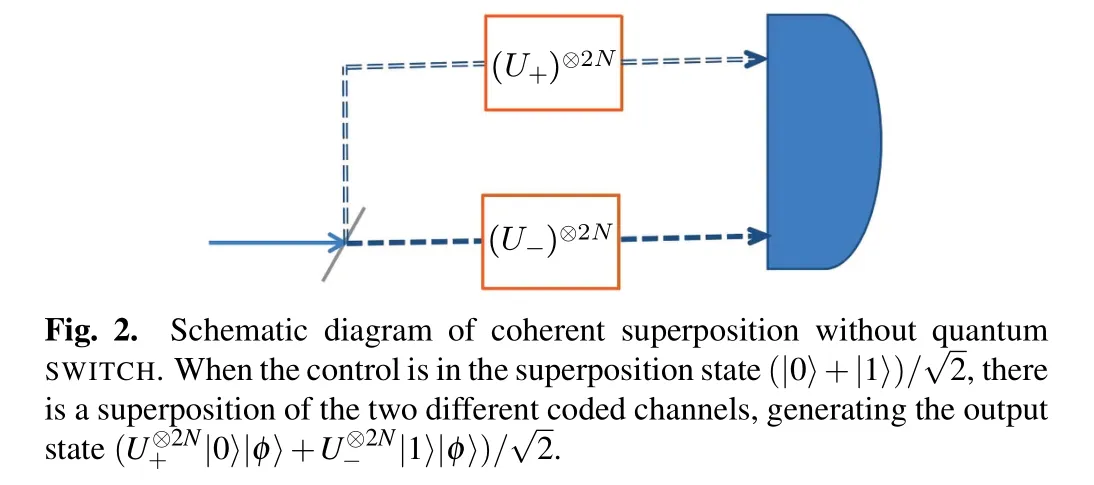
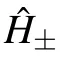

The estimation precision ofθ2can be described as
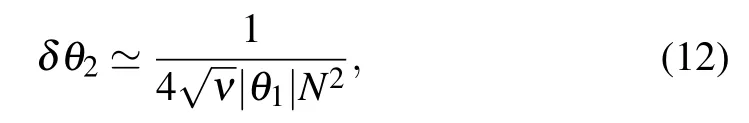
where we also consider the largeνlimit.Comparing Eq.(8)with Eq.(28),we can see that

where“cs”denotes the coherent superposition and“qs”denotes the quantum SWITCH.This shows that the coherent superposition without quantum SWITCH can perform better than the case with quantum SWITCH in estimatingθ2(the results are similar for parameterθ1).
More importantly,the strategy of coherent superposition of two different coded channels can be realized by a simple Hamiltonian of composite system model
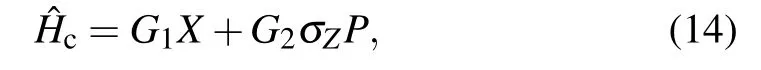
where the Pauli operatorσZ=|0〉〈0|?|1〉〈1|.Such Hamiltonian can be obtained from a dispersive Jaynes-Cumming Hamiltonian which has been experimentally shown in superconducting circuits[24]or a two-tone drive which has been experimentally demonstrated in trapped ions.[25,26]With the initial direct product state(|0〉+|1〉)|φ〉,the output state at time T is given by
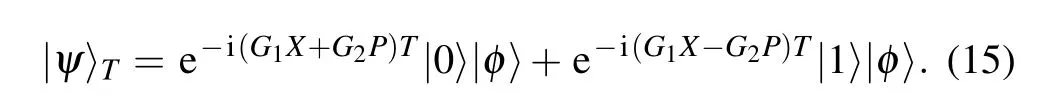
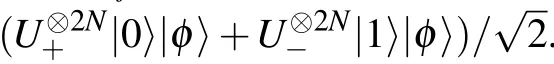
4.Nonlinear Hamiltonian
In a continuous variable nonlinear system,we first consider a simple nonlinear Hamiltonian,(H1=X,H2=P2).
In the largeνand N limit,the estimation precision ofθ2can be calculated by the above way and the communication relation[X,[X,P2]]=?2,
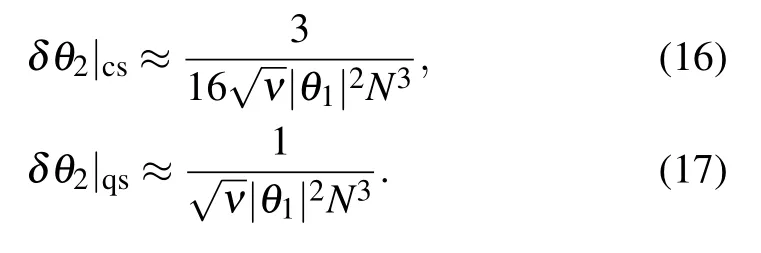
From the above equations,one can see that both strategies can obtain higher estimation precision with super-Heisenberg scaling 1/N3.It demonstrates that nonlinear Hamiltonian can further improve the estimation precision based on the two strategies.And the strategy with the coherent superposition can still perform better than the case with the quantum SWITCH.The radio betweenδθ2|csandδθ2|qsis

which means that compared with the linear case,the nonlinearity increases the advantage of strategy with the coherent superposition over the strategy with the quantum SWITCH in parameter measurement.
Then,we consider a general nonlinear Hamiltonian,(H1=X,H2=Pm)for integer m>1.We can analytically obtain the estimation precision ofθ2by induction(see Appendix A)
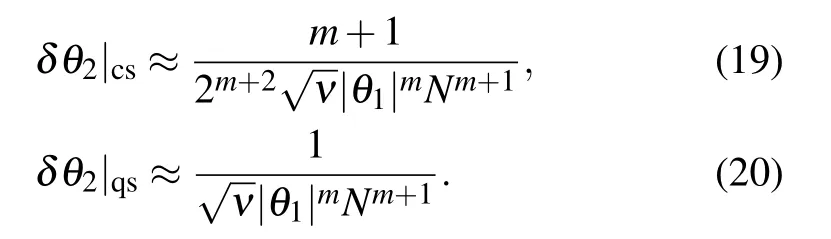
From the above equations,we can see that the super-Heisenberg limit 1/Nm+1is achieved.It means that the estimation precision can be further improved as m.
After a simple calculation,the radio in the case of the general nonlinear Hamiltonian is described as
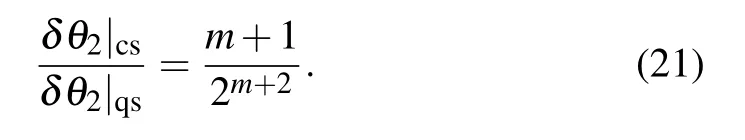
As m increases,the ratio gets smaller and smaller.It shows that the advantage of strategy with the coherent superposition over the strategy with the quantum SWITCH has been further extended due to the nonlinear Hamiltonian.
5.Potential application
Firstly,we consider that a optomechanical system is formed by a Fabry–P′erot cavity with a moving-end mirror.The Hamiltonian of the system is described as[27,28]
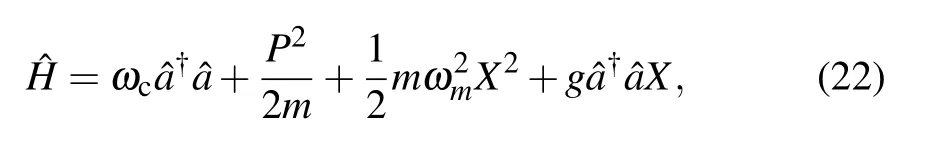
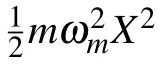
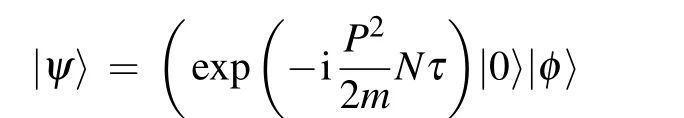
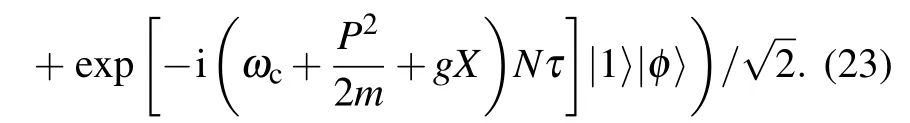
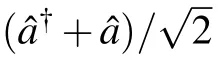
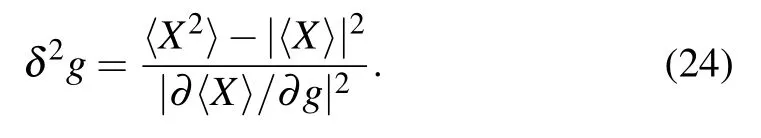
By analytical derivation,we can obtain the estimation precision of g for large N
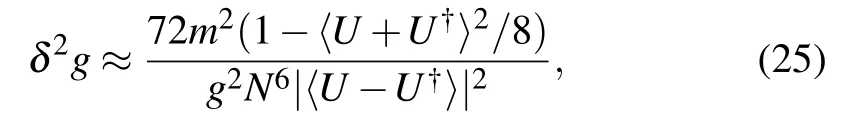
where
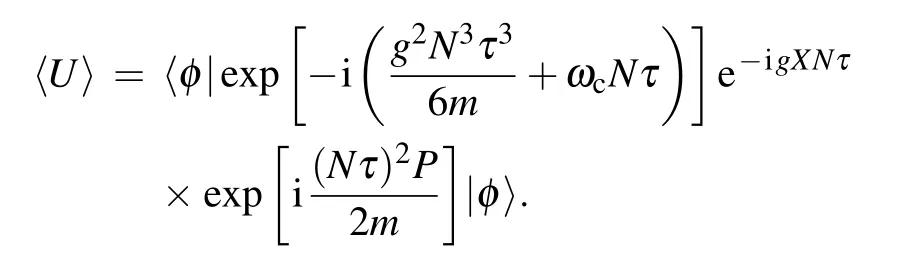
Obviously,we can see that the super-Heisenberg scaling 1/N3has been achieved by the homodyne detection.
Secondly,we consider that a two-level system couples with an oscillator system via dephasing couplingσZ?P,which could be realizable in superconducting qubit-oscillator devices.[31–33]The Hamiltonian of whole system is described as follows:
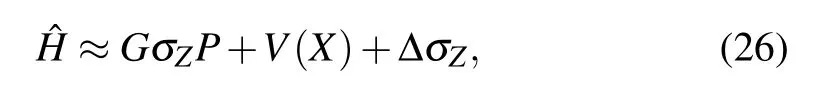
where we omit the free Hamiltonian of low-frequency oscillator for the case of strong coupling[34]and V(X)denotes the nonlinear potential.For example,the nonlinear potential for Duffing system is V(X)=βX4.[35]By the similar calculation,we find that the estimation uncertainty of the coupling strength G and the constantβare proportional to 1/N5.
Thirdly,we consider the gravitational time dilation.The total Hamiltonian of the system is[36]
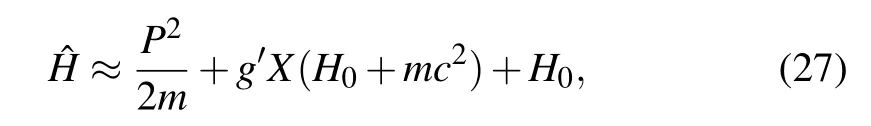
Fourthly,our work can further test the modification of the canonical commutation relations,[38][X,P]=i(1+αP2),where the coefficientα?1.We consider the strategy of coherent superposition with a general nonlinear Hamiltonian,(H1=X,H2=Pm).The output state is described as
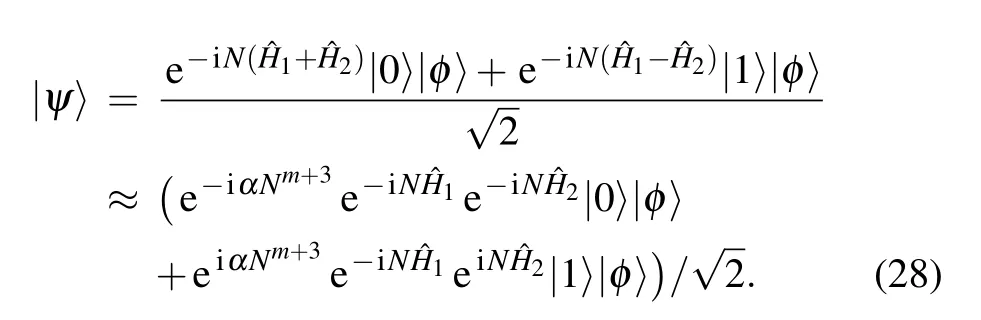
As a result,we find that the scaling of the uncertainty ofαis 1/Nm+3.In other words,the nonlinear Hamiltonian can effectively improve the estimation precision ofα,which will help to test the modification theory of the canonical commutation relations.
6.Conclusion and outlook
We have proposed the strategy of coherent superposition of two different coded channels and shown that super-Heisenberg scaling can be achieved in the continuous variable system.In the case of linear Hamiltonian,the strategy of coherent superposition can improve the parameter estimation precision by 4 times compared with the strategy of quantum SWITCH.In the case of nonlinear Hamiltonian,the enhanced scaling 1/Nm+1with integer m>1 can be obtained.And the nonlinearity further increases the advantage of strategy with the coherent superposition over the strategy with the quantum SWITCH in parameter measurement.Our results provide a high-precision measurement method,which has a potential application in estimating the coupling strength of the optomechanical system and Duffing system.In addition,by enhancing the estimation precision of the gravitational acceleration,the theory of time dilation can be further checked.And we further demonstrate that the nonlinearity can offer a better way to test the modification of the canonical commutation relation.
Adverse conditions,such as uncontrolled environmental disturbances,generally play a detrimental role in quantum metrology.The further works can be the study of the strategy of coherent superposition of different coded channels in decoherence environment.
Appendix A.Exponential commutation relation
The expressions of the exponential commutation relation can be described as
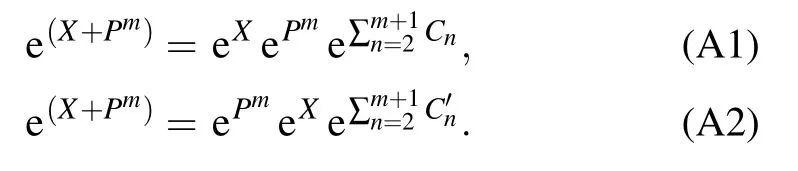
ProofLet us first set
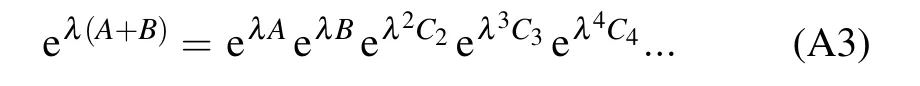
By differentiating both sides of Eq.(A3)with respect toλand multiplying it from the right by e?λ(A+B),we can obtain
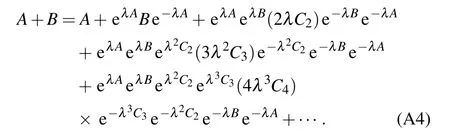
Substituting the known formula
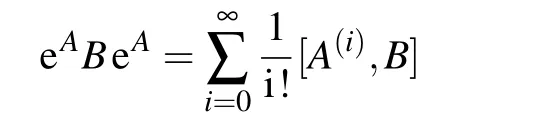
into the above equation,one can obtain
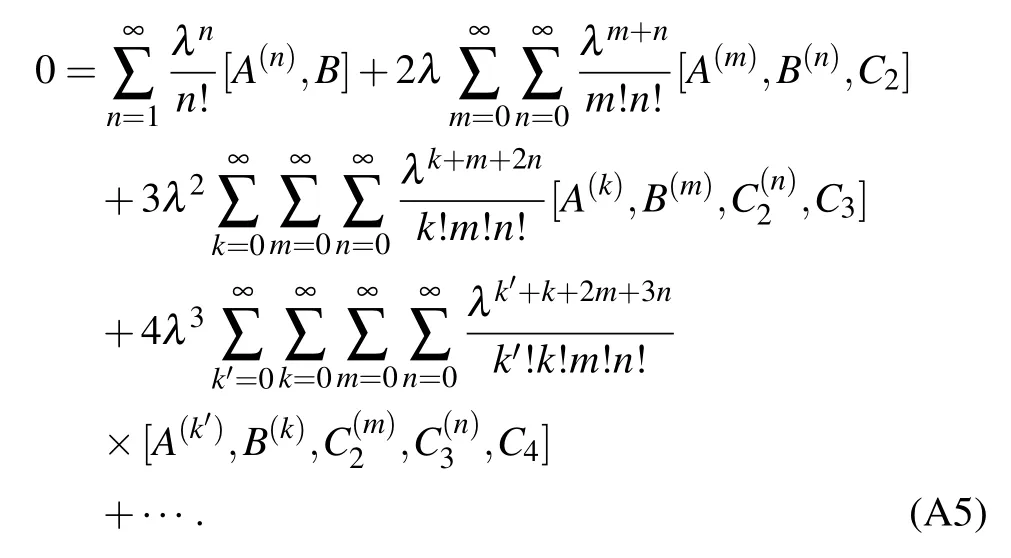
in which
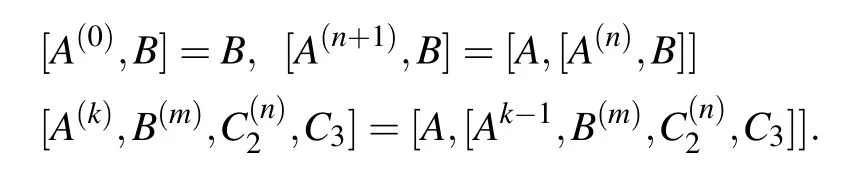
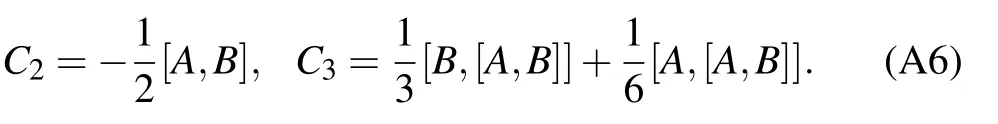
Based on the above equation,we can obtain the detailed form of Cn,such as,In principle,the formula can be derived by Eq.(A6).However,one cannot obtain the general simplified form of Cnfor any n.It cannot be written in a compact form.
Fortunately,when A=X and B=Pm,we can obtain a simple results by the following induction:
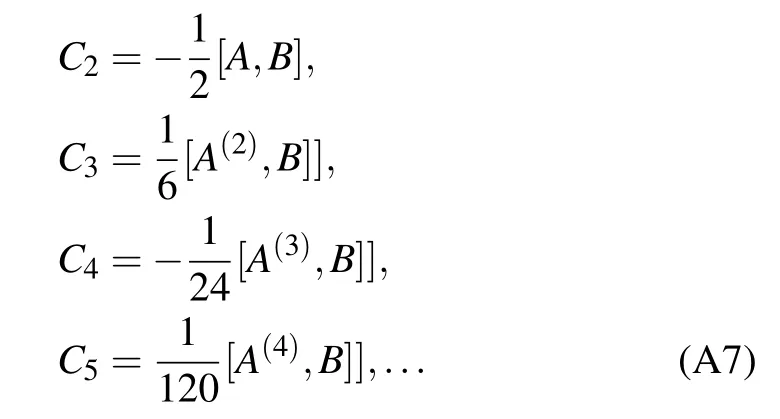
According to the above equations,we can get
Forλ=1,the exponential commutation relation is described as
When A=Pmand B=X,we can get
Forλ=1,the exponential commutation relation is described as
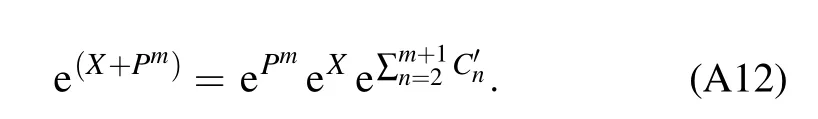
Appendix B.Measurement with the strategy of the coherent superposition
Utilizing Eq.(A8),we can express the output state in the case of the coherent superposition

Then,the quantum Fisher information can be achieved by Fθ=4(〈?θψ|?θψ〉?|〈?θψ|ψ〉|2).As a result,we obtain the general formula
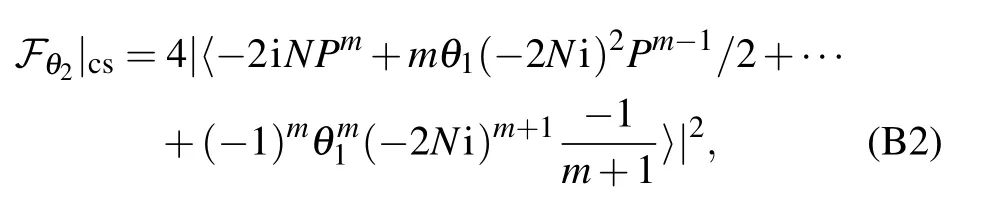
where〈·〉=〈φ|·|φ〉.For N?θ1〈P〉,
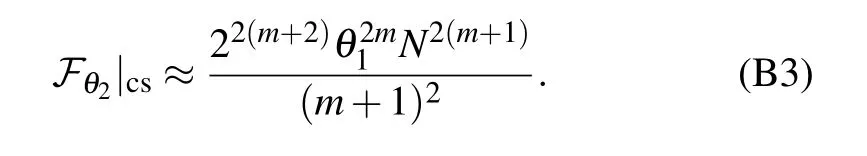
Apprndix C.Measurement with the strategy of the quantum SWITCH
Utilizing Eq.(A12),we can express the output state in the case of the quantum SWITCH
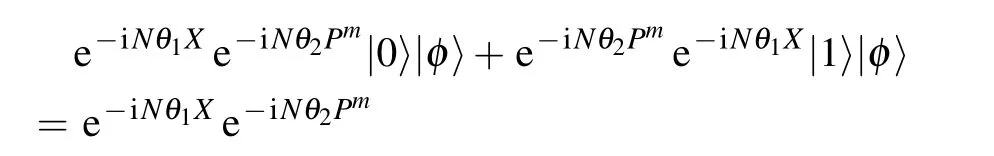
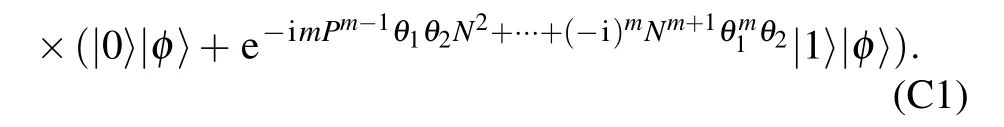
Then,the quantum Fisher information can be achieved by the similar way
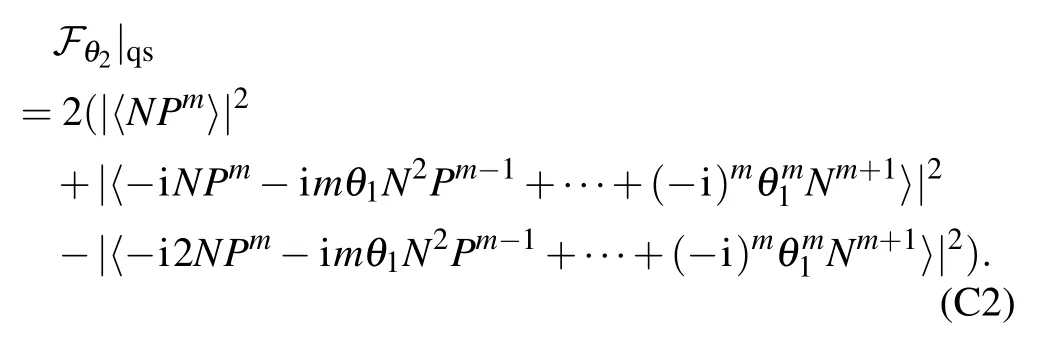
For N?θ1〈P〉,the above equation can be simplified as
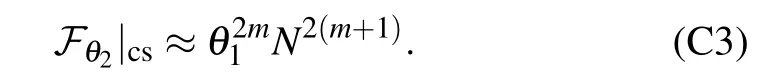
- Chinese Physics B的其它文章
- Origin of anomalous enhancement of the absorption coefficient in a PN junction?
- Protection of isolated and active regions in AlGaN/GaN HEMTs using selective laser annealing?
- First-principles study of plasmons in doped graphene nanostructures?
- Probing thermal properties of vanadium dioxide thin films by time-domain thermoreflectance without metal film?
- An improved model of damage depth of shock-melted metal in microspall under triangular wave loading?
- Signal-to-noise ratio of Raman signal measured by multichannel detectors?

