模塊化多電平換流器單極接地故障電流計算

范娜麗 沈兵 黃靖

摘 要：基于模塊化多電平換流器的直流系統的單極接地故障是一種常見的故障類型，接地故障電流暫態特性的分析對于故障檢測、保護設置、系統參數的進一步優化都具有非常重要的工程實際意義。首先，在基于MMC拓撲結構的中壓直流系統一定的調制策略基礎上，通過分析故障電流的流通路徑，對直流側發生單極接地故障的故障特性進行了分析;然后，利用復頻域分析法得到單極接地故障時的等效電路，通過計及故障時刻各相橋臂子模塊投入數量，對各相橋臂在單極接地故障時刻的電容進行了等效，再根據疊加定理進行了換流器閉鎖前的接地故障電流的理論推導;最后，得到單極接地故障電流值隨故障時刻和交流側接地電阻變化的規律，并通過PSCAD/EMTDC 進行仿真計算，通過對比分析驗證了接地故障電流理論計算的正確性。

關鍵詞：模塊化多電平;單極接地故障;故障電流;接地方式

Abstract：Pole-to-ground fault of DC system based modular multilevel converter（MMC） is the most common type of fault. The analysis of the transient characteristics of the fault current has practical engineering significance for fault detection， protection setting and further optimization of system parameters. Firstly，based on the topological structure and modulation strategy of MMC of DC system， the fault current path is pointed out and the fault current characteristics of the pole-to-ground fault on the DC side are analyzed. Secondly， the equivalent circuit for pole-to-ground fault was obtained by using the complex frequency domain analysis method. Even the capacitance of each phase bridge arm at pole-to-ground fault is equivalent by counting the number of the sub-modules of each phase bridge arm at the fault time. Then the grounding fault current before IGBT blocking was derived theoretically according to the superposition theorem. Finally， the law of the change of pole-to-ground fault current with the fault time and the grounding resistance of the AC side is obtained. The correctness of the theoretical calculation of the grounding fault current is verified by comparative analysis with the simulation calculation of PSCAD/EMTDC.

隨著新能源的廣泛應用、電力電子技術和計算機技術的發展以及用戶對電能質量的要求日益提高，直流輸、配電技術應運而生[1-2]。在直流技術出現的早期，主要是以兩電平電壓源換流器（Voltage Source Converter， VSC）為主，而近些年MMC（Modular multilevel converter， MMC）換流器相較VSC換流器具有動態均壓要求降低、開關頻率低、損耗成倍下降、電壓諧波含量低、故障處理能力強等一系列的優點[3-5]，因此受到學術界和工業界的廣泛關注，且得到了廣泛的應用。目前關于MMC直流系統的單極接地故障的研究，主要集中在故障暫態特性的定性分析、控制保護策略、接地電阻對故障特性的影響等[6-14]，對于MMC直流系統單極接地故障電流的解析計算相對較少。文獻[7]從不平衡電壓恢復的理論出發，假設電路結構三相對稱，計算換流器故障極橋臂每相的零序故障電流，從而得出交流側接地電阻值選取的原則，但沒有考慮到故障極橋臂的每相子模塊投入數量不等，可能導致電路結構的不對稱。文獻[8-9]忽略子模塊投切數量的變化，將閉鎖前的單端單相上橋臂等效為一個電容值為2C0/N（C0為子模塊電容值，N為單相上下橋臂投入值的子模塊數的總和）或12C0/N，得到故障電流的計算式，忽略了單極接地故障時橋臂子模塊投切狀態的實時變化對接地點故障電流精確計算的影響。文獻[10]分析了真雙極系統的單極接地故障特性，提出由于真雙極系統直流側存在接地極的結構特點，得出單極接地故障特性與偽雙極系統的雙極短路故障的研究在原理上是相同的，因此關于單極接地故障的研究主要集中在偽雙極直流系統中。文獻[11]把基于架空輸電線的高電壓大容量MMC-MTDC系統采用一階電壓源的一階回路的簡化模型，利用三要素法列寫了單極接地故障電流。沒有考慮限流電抗器和橋臂電抗器上分壓的作用。文獻[12]在一定的假設條件下，通過均值等效的方法得到等效放電電容的解析計算式，在此基礎上，得到影響等效放電電容的因素：調制比和短路時刻，進一步分析調制比和短路時刻對等效放電電容的影響規律，沒有進行單極接地故障電流的計算。文獻[13]在充分考慮到橋臂子模塊投入和切除的情況，在均壓條件下建立了由電容器和子模塊投入函數共同決定的橋臂電壓電流的數學模型，結合狀態方程數值解法，計算了MMC直流故障時橋臂故障電流和極間故障電流，但沒有計算對直流側單極接地故障的故障電流。文獻[14]在交流側采用接地方式下的MMC-MTDC系統中，考慮故障時刻橋臂子模塊投入個數且已知初始狀態的RLC二階電路，指出電路中的的等效電容相當于N/nref個C0/nref電容并聯，根據初始狀態得出故障電流和電容電壓解析式，但僅計了算橋臂故障電流，未進行接地點故障電流的計算和仿真驗證。

由于單極接地故障的故障電流與MMC拓撲結構和調制方式有關，首先對工程中廣泛采用的偽雙極結構的MMC的拓撲結構、子模塊的工作狀態及調制策略進行了介紹，進一步提出實時狀態下子模塊投切數量的數學模型，并在均壓策略下計算了單相單橋臂等效電容值;然后，利用復頻域法對單極接地故障情況下單端MMC換流器進行等效變換，再利用疊加定理計算單極接地故障時接地點的故障電流，并歸納出單極接地故障電流隨故障時刻和接地電阻值不同時的變化規律;最后，利用仿真軟件搭建了MMC系統的仿真模型，對單極接地故障電流進行仿真計算，驗證了理論計算結果的正確性。

1 MMC中壓直流系統的概述

1.1 MMC的拓撲結構

由N個串聯的半橋子模塊SM和一個橋臂電抗器L0組成單個橋臂，再由上下兩個橋臂合成一個相單元，由三個相單元組成MMC換流站[6，15]，MMC拓撲結構如圖1（a）所示，圖中Uvj和ivj（j=a，b，c）表示MMC換流器交流側相電壓和相電流;Upj、Unj分別為j相上、下橋臂電壓;ipj、inj分別為j相上、下橋臂電流，Udc表示直流側極間電壓。其中子模塊SM主要包含三種：半橋型、全橋型和混合型。由于半橋型MMC開關器件較少、導通損耗低、傳輸效率高、具有良好的經濟性[16]，工程上得到了廣泛應用，如圖1（b）所示，半橋子模塊由兩個絕緣雙極型晶閘管（Insulated Gate Bipolar Transistor， IGBT）、反并聯二極管以及電容C0組成，圖1（b）中VT1、VT2代表IGBT，VD1、VD2代表反并聯二極管，UC代表電容電壓，USM為子模塊的輸出電壓，iSM為流入子模塊的電流[17]。

1.2 調制策略和子模塊工作狀態

MMC的調制策略主要有兩種：階梯波調制策略和PWM（Pulse Width Modulation）策略，當子模塊數較多時，利用階梯波調制的波形質量高等優勢顯著;當子模塊數較少時，采用PWM調制波形質量好。針對子模塊數量相對較少情況下進行研究，因此采用PWM調制策略，其原理是通過調制波和三角波的關系來控制子模塊中開關管VT1和VT2的導通。當調制波大于三角載波時，半橋子模塊的VT1導通，VT2關斷;當調制波小于三角載波時，半橋子模塊的VT2導通，VT1關斷。如圖2所示，紅色的正弦波表示調制波，調制波的相電壓幅值為mUdc/2，m表示調制比，三角載波角度依次相差2π/N，N表示單相單橋子模塊數，其中上下橋臂子模塊的調制波反相。

根據VT1和VT2的導通狀態的不同可以把半橋子模塊的工作狀態分為3種[15]，如表1所示。

（1）閉鎖狀態：VT1、VT2都加關斷信號，對于模式1，電流經過VD1給電容充電;對于模式4，電流經過VD2將電容旁路，這兩種模式均屬于非正常工作狀態。

（2）投入狀態：VT1加開通信號而VT2加關斷信號，處于模式2時，電流經過VD1向電容器充電;處于模式5時，電流經過VT1使電容放電。

（3）切除狀態：VT1斷加關斷信號VT2加開通信號，處于模式3時，電流經過VT1將電容器旁路;處于模式6時，電流經過VD2將電容器旁路。

2 直流故障特性分析和故障電流計算

基于MMC直流系統的單極接地故障與接地方式有關，而MMC系統的接地方式又可以分為直流側接地方式和交流側接地方式[19-21]，其中直流側接地方式包含直流側箝位電阻中點接地方式;交流側接地方式包含聯接變壓器星形經電阻接地，星形電抗中性點經電阻接地方式和接地變壓器接地方式。對于分析單極接地故障，由于采用箝位電阻中點接地方式，不存在接地故障電流回路，此處不再贅述。而對于交流側采用的三種接地方式在進行直流側單極接地故障的數值等效電路是類似的，因此主要針對交流側變壓器中性點經電阻接地方式下，直流線路單極接地故障進行分析和研究。

對于交流側變壓器中性點經電阻接地方式下，單極接地故障的初始時期，接地點故障電流主要由橋臂子模塊電容的放電電流和直流母線對地電容放電電流組成。由于在中壓直流系統中，電壓等級較低，線路對地電容的放電電流較小，此處故障電流僅考慮子模塊電容放電電流的影響。

MMC直流系統發生單極接地故障后，子模塊電容放電電流上升極快。為了保護換流器電力電子器件不受損壞，需要在檢測到直流側故障后迅速將IGBT閉鎖，IGBT閉鎖后，子模塊電容不再放電，橋臂子模塊的電容也不再給接地故障點提供故障電流，因此僅考慮IGBT閉鎖前的故障電流的計算。

2.1 直流單極故障特性分析

對于單極接地故障，以MMC直流系統換流器出口處發生正極接地故障對電力電子設備危害最大。換流器出口處發生單極接地故障后，故障橋臂和直流線路上的電流主要有正常工作電流和故障通路中子模塊電容放電形成的故障電流組成[11]，交流側接地極和直流側故障點僅流過電容放電電流。故障初期控制方式保持不變，故障后到IGBT閉鎖前的極短時間內，子模塊的投切方式不發生變化，因此故障電流決定于故障前子模塊的投切狀態。對于投入的子模塊，無論是故障時電容放電電流還是正常運行的電流，均流過此;而對于切除狀態的子模塊，電容放電電流和正常運行電流均從下開關管VD2流過，不經過子模塊電容。故障發生后到IGBT閉鎖前，故障電流流通路徑為故障點→交流側接地極→變壓器→3個并聯的相單元→平波電抗器→直流斷路器→直流線路→故障點。如圖3中紅色線所示，給出了某一時刻發生故障時故障電流的流通路徑，可以看出在發生單極接地故障后，橋臂里的等效電感L0和電阻R0值是定值，與發生單極接地故障的時刻無關。而故障時每相橋臂投入的子模塊數量不等，即參與放電的電容器數量不等，可能導致每相故障橋臂流過的故障電流值不等，因此接地點的故障電流值也可能不相等，且故障電流不僅與每個橋臂投切的子模塊數量有關，也與發生故障的時刻有關系。

2.2 MMC單極接地故障下等效電路

考慮到橋臂子模塊的投切數量的實時變化，本質上MMC是一個非線性時變電路，但由于故障發生到IGBT閉鎖前，這段時間極短。在極短的時間內，子模塊的控制策略依然工作在正常的投切狀態，MMC中6個橋臂投入的子模塊和切除的子模塊數均保持不變。在以上假設條件下，MMC可以看成一個線性定常電路。對于線性定常電路，可以采用運算電路分析法（或稱復頻域分析法）進行暫態過程分析[15]，其具體做法是把阻抗和導納分別用運算阻抗和運算導納進行替代，對電路元件的微分方程作拉普拉斯變換，從而將時域中的暫態電路求解問題變換到復頻域（即s域）下進行求解。即將圖3所對應的時域模型變換成復頻域中的運算電路模型，如圖4（a）所示，圖4（b）為簡化等效電路。其中L0和R0表示橋臂里的等效電感和電阻，sLdc表示復頻域下直流側線路電感和平波電抗器的電感之和，Rdc表示直流側線路的電阻值，Lac和Rac表示交流側等效電感和等效電阻，Rf表示交流側接地極的接地電阻值。復頻域下等效電路中的電容值與子模塊的投切數量和短路時刻密切相關，這將在下一節探討。

2.3 單極接地故障等效電容的計算

以A相為例，對單極接地故障下的MMC的放電電容進行等效，假設故障時刻交流側A相電壓的初始相角為θ，故障時的交流側A相的相電壓記為：

2.4 MMC單極接地故障時故障電流的計算

故障時刻各相橋臂投切的子模塊不相等，因此圖4（b）所示電路是一個三相不對稱電路。由2.2節假設MMC就是一個線性電路，利用線性電路的疊加原理對接地點故障電流進行計算，因此把圖4（b）等效為三個電源單獨作用，進行接地點故障電流的計算，然后進行疊加。此處僅顯示A相電源作用時的等效電路圖，如圖5所示。

等效電路和電路中的元器件參數都已知，下面進行接地故障電流的計算，首先給出MMC換流站的系統參數如表2所示。故障電流計算時忽略直流側電路的對故障電流的影響，同時忽略交流側電阻Rac和橋臂中電阻R0的作用。

為方便觀察，圖8僅給出在A相相電壓的相角為0°，30°和90°的接地故障電流波形圖，圖9給出出了不同故障時刻的接地故障電流變化率的波形圖，為了對比分析方便，圖8和9中所有的波形都換算到0s時刻的坐標軸下。可以看出當A相相電壓的相角為0°，即A相相電壓過零發生正極接地故障，接地點故障電流值較小，故障電流的變化率也較小;當A相相電壓的相角為90°，即A相電壓達到正的幅值發生故障，接地點故障電流值較大，故障電流的變化率也較大;當A相相電壓的相角為30°，即B相達到負的幅值發生正極接地故障時，其接地點故障電流值介于兩者之間，故障電流的變化率也介于兩者之間。

綜上所述，在三相中某一相相電壓達到正的幅值時，直流側正極接地故障的故障電流值最大，可以用來校驗MMC換流器的關鍵電氣設備的過電流水平和接地電阻值的選取;當某一相過零時，正極接地故障的故障電流值最小，可以用來校驗接地保護裝置中故障檢測的靈敏度;當某一相的相電壓達到負的幅值時，正極接地故障的故障電流值介于兩者之間。

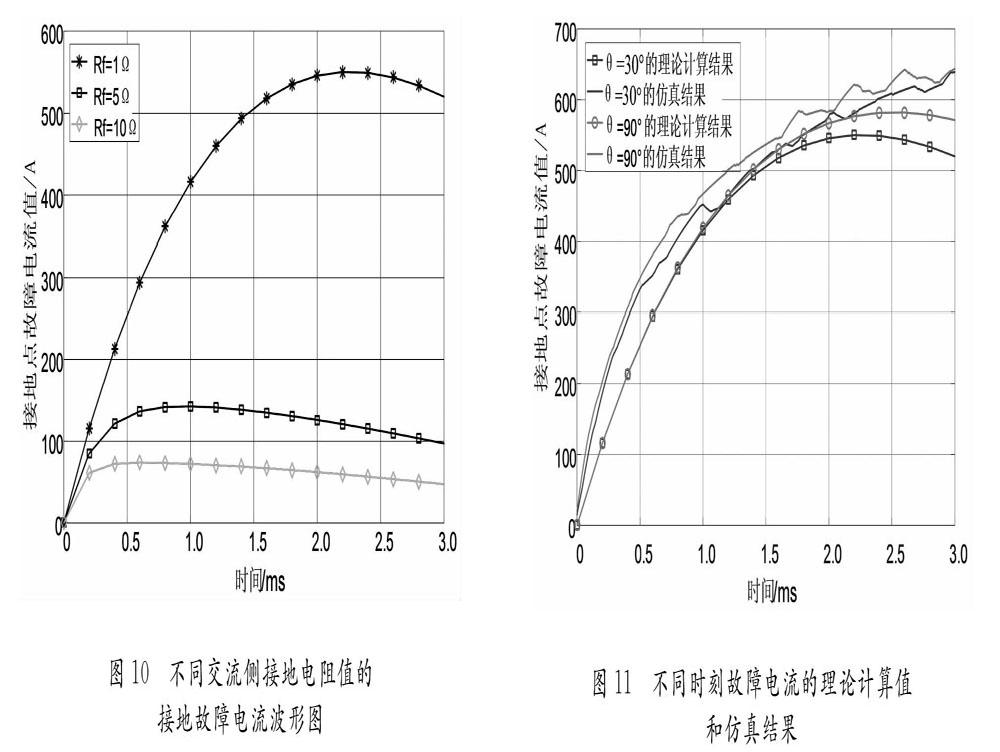
以上分析均是基于交流側變壓器中性點接地電阻Rf為1 Ω，發生金屬性接地故障進行的。單極接地故障電流同樣受到接地電阻值Rf和接地故障時的過渡電阻的影響。不同接地電阻值Rf對應的故障電流波形，如圖10所示。可以看出接地故障電流與接地電阻Rf成反比，隨著交流側接地電阻值的增大，故障電流變小，當接地電阻值趨于無窮大時，相當于交流側變壓器中性點不接，不構成子模塊電容放電回路，接地故障電流值為0。如果單極接地故障發生的是非金屬性故障，接地過渡電阻的增加與增大交流側接地電阻對接地點的故障電流影響是一樣的，不再贅述。

3 仿真驗證

3.1 仿真平臺

利用電磁暫態軟件PSCAD/EMTDC搭建MMC直流系統的仿真模型，通過仿真計算MMC直流系統單極接地故障的故障電流，并對仿真結果和理論計算值進行比較分析，其中仿真模型中的系統參數如表2所示。

3.2 仿真分析

在仿真軟件中搭建基于MMC的直流系統結構，待系統正常穩定運行后，分別當換流器交流側A相的相角θ達到30°，60°和90°時刻，在換流器出口處設置正極接地故障，并對正極接地故障電流進行仿真計算，計算結果如圖11所示，并對相同條件下的理論計算值與仿真計算結果進行比較，為了對比分析方便，把所有的波形都換算到0 s時刻的坐標軸下，可以看出不同時刻的接地故障電流值的計算值比仿真結果偏低，是因為在理論等效中沒有考慮橋臂電感的作用。但是每個時刻的故障電流的理論計算值與仿真值相差較小，實際工程應用中將理論計算值乘以一個可靠系數，可以作為設備參數選型、接地電阻地選取以及接地故障保護設置的理論依據。同時可以注意到，在前2 ms內理論計算值和仿真結果十分吻合，2 ms以后理論計算值有所下降，而仿真計算結果卻一直處于上升的趨勢，是因為理論分析中假設發生接地故障初期，在定電壓控制策略下，橋臂中投入放電的電容數量不變，實際運行中隨著電容放電，電壓失調，橋臂中參與放電的數量有所變化，且隨著時間的變化，控制方式也發生了變化。但2 ms之前的故障波形值已足以正確反映接地故障的電流值的大小和變化率，為IGBT閉鎖和故障檢測提供了有效的信息。

在接地電阻值Rf不同，相同時刻發生單極接地故障時，仿真計算結果如圖12所示。由圖12可知換流器交流側接地電阻值越大，故障電流越小，且理論分析值與仿真結果越接近，說明單極接地故障電流的理論計算方法為小電流系統的接地故障電流的計算提供了更加有效的理論支撐。

4 結 論

首先單極接地故障的故障特性和流通路徑，對不同時刻故障極橋臂電容進行等效，然后利用復頻域分析法和疊加定理，建立單極接地故障的等效模型并進行簡化。在此基礎上，提出了一種計算直流側單極接地故障的方法，并對不同時刻的接地故障電流值與仿真結果進行對比驗證，得出如下結論：

（1）此方法可以同時計算得到單相故障橋臂和直流側接地點故障電流的數值解，且計算方法簡便易實現。通過仿真驗證，說明此方法也比較準確。

（2）通過交流側相電壓的不同初相角θ 單極接地故障電流的理論計算和仿真驗證，發現了單極接地故障受故障發生時刻的影響，并揭示了其規律。

（3）提出的橋臂等效電容和復頻域方法進行接地故障電流的理論計算較準確，對實際工程的接地電阻的選取和小電流接地系統中故障檢測裝置的靈敏性校驗都具有重要的理論指導意義。

參考文獻

[1] 宋強， 趙彪， 劉文華， 等. 智能直流配電網研究綜述[J]. 中國電機工程學報， 2013， 33（25）： 9-19.

[2] 鄭歡， 江道灼， 杜翼， 等. 交流配電網與直流配電網的經濟性比較[J]. 電網技術， 2013， 37（12）： 3368-3374.

[3] 趙旭陽， 王聰， 牛勝鎖， 等. 綜合考慮中性點接地方式和網架結構的配電網供電可靠性的評估[J]. 電測與儀表， 2019， 56（18）： 49-56.

[4] DEBNATH S， QIN J， BAHRANI B， et al. Operation， control，and applications of the modular multilevel converter： a review[J]. IEEE Trans. Power Electro， 2015， 30（1）： 37-53.

[5] DEKKA A， WU B， FUENTES R L， et al. Evolution of topologies， modeling， controls schemes， and applications of modular multilevel converters[J]. IEEE Journal Of Emerging and Selected Topics In Power Electronics， 2017， 5（4）： 1631-1656.

[6] 趙成勇， 李探， 余露杰， 等. MMC-HVDC直流單極接地故障分析與換流站故障恢復策略[J]. 中國電機工程學報， 2014， 34（21）： 3158-3526.

[7] 李蕊， 羅飛， 焦在濱. 中壓直流配電系統接地方式研究[J]. 電網技術， 2018， 42（8）： 2594-2603.

[8] 楊海倩， 王瑋， 荊龍， 等. MMC-HVDC系統直流側故障暫態特性分析[J]. 電網技術， 2016， 40（1）： 40-46.

[9] 李俊松， 張英敏， 曾琦， 等. MMC-MTDC系統單極接地故障電流計算方法[J]. 電網技術， 2019， 43（2）： 546-553.

[10]陳繼開， 孫川， 李國慶， 等. 雙極MMC-HVDC系統直流故障特性研究[J]. 電工技術學報， 2017， 32（10）： 53-68.

[11]XUE Shi-min， Jie Lian， QI Jin-long， et al. Pole-to-ground fault analysis and fast protection scheme for HVDC based on overhead transmission lines[J]. Energies， 2017，10（7）：1059.

[12]段國朝， 王躍， 尹太元， 等. 模塊化多電平變流器直流短路故障電流計算[J]. 電網技術， 2018， 42（7）： 2145-2152.

[13]蔡洋， 郭文勇， 趙闖， 等. 模塊化多電平換流器直流故障過電流精確計算與分析[J]. 電工技術學報.http：//doi.org/10.19595/j.cnki.1000-6753.tces.L90188.

[14]羅永捷， 徐羅那， 熊小伏， 等. MMC-MTDC系統直流單極對地短路故障保護策略[J]. 電工技術學報， 2017， 32（1）：98-106.

[15]徐征等. 柔性直流輸電系統[M]. 2 版. 北京： 機械工業出版社， 2010.

[16]薛源.采用載波移相調制的模塊化多電平換流器分析研究[D]. 武漢：華中科技大學， 2017.

[17]趙成勇， 李路遙， 翟曉萌， 等. 一種新型模塊化多電平換流器子模塊拓撲[J]. 南方電網技術， 2012， 6（6）：62-66.

[18]NGUYEN T H， KHALIFA A H， MOURSI M S. Alternating submodule configuration based MMCs with carrier-phase-shift modulation in HVDC systems for DC-fault ride-through capability[J]. IEEE Transactions on Industrial Informatics， 2019：1-1.

[19]戴志輝， 黃敏， 蘇懷波. 基于MMC的環狀直流配電網在不同接地方式下的故障特性分析[J]. 電力系統保護與控制，2019，47（1）：1-10.

[20]鄧旭， 沈揚， 王東舉， 等. 基于模塊化多電平換流器的多端柔性直流系統接地方式[J]. 電力建設，2014，35（3）：24-30.

[21]王璐瑤， 詹昕， 高仁棟， 等. 基于模塊化多電平換流器的直流配電網接地方式選擇[J]. 供用電， 2020， 37（5）：2-10.