加溫加壓下CFD-PBM 耦合模型空氣-水兩相流數值模擬研究

張文龍，侯燕，靳海波，馬磊，何廣湘，楊索和，郭曉燕，張榮月

（1 北京石油化工學院化學工程學院，北京 102617；2 燃料清潔化及高效催化減排技術北京市重點實驗室，北京 102617）

引言

鼓泡塔反應器因操作方便、結構簡單、傳質和傳熱性好等優點，被廣泛地應用在化學、石油化工、生化、制藥和冶金等行業[1-3]。鼓泡塔中典型的反應有費-托合成、甲醇的合成以及PX 氧化反應，這些反應需要在高溫高壓的反應器中進行。由于鼓泡塔中的氣液兩相流非常復雜，尤其是在高溫和高壓條件下，需要進行實驗或數值模擬以獲得一些重要參數，如氣含率、氣泡大小分布、液體速度分布和氣泡上升速度等，以分析塔中的流體動力學行為與傳質特性。在這些參數中，氣含率是影響鼓泡塔中流體行為的最重要參數之一，大多數氣含率是常溫和常壓下的實驗數據。而在工業生產中，鼓泡塔中的反應通常在升溫加壓的條件下完成。因此，了解近實際工況下鼓泡塔流體力學特性將更有意義。

近幾十年來，國內外開展了廣泛的氣-液鼓泡塔內的實驗和模擬研究，現有文獻研究較多的是壓力變化對氣含率的影響，而升溫對氣液兩相鼓泡塔影響在文獻中較為少見，主要研究物性變化的影響規律[4]。Deckwer 等[5]以Fischer-Tropsch 過程為背景，在直徑為4.1 cm 和10 cm 的漿液鼓泡塔反應器中研究了溫度和壓力變化對氣含率和傳熱傳質的影響。Behkish 等[6]對N2、He/異構烷烴體系研究發現，在溫度30～200℃范圍內，總氣含率隨溫度的升高而增加，加入固相后，增加的固體濃度會使氣含率顯著降低。Pohorecki 等[7]在0.3 m 鼓泡塔中研究了N2在環己烷中的流體力學行為，發現溫度升高導致液體表面張力降低，氣含率增加，而平均氣泡直徑隨溫度升高而降低。升溫更多表現為氣液物理性質的變化，而對氣泡行為的影響尚未完全揭示，或者缺乏準確統一的解釋。因此，研究溫度變化對氣含率的影響機理具有十分重要的意義。

計算流體力學（CFD）方法已經成為鼓泡塔反應器模擬和優化的重要工具。計算流體力學與群體平衡模型結合（CFD-PBM）可有效地模擬鼓泡塔內流體行為[8]。對于鼓泡塔中的氣液兩相流動常見的模擬方法有歐拉-歐拉方法和歐拉-拉格朗日方法。歐拉-歐拉模型假設氣液兩相之間相互滲透，不直接追蹤每一個氣泡的運動，大大降低了計算量而被廣泛應用[9-10]。歐拉-歐拉模型需要相間作用力來進行封閉，而曳力是氣-液系統中一種最重要的作用力，其直接影響模擬結果的準確性[11-13]。目前，單氣泡曳力模型到氣泡群曳力模型的轉變較為復雜。Buffo 等[14]發現CD（氣泡群曳力系數）等于CD（0單氣泡曳力系數）乘以與液含率有關的系數。而在氣液鼓泡塔的模擬中，氣泡群曳力系數較為常用。Roghair 等[15]在歐拉-拉格朗日模型基礎上，采用直接模擬得到氣泡群曳力的閉合模型。Wang 等[16]在Tomiyama[17]單氣泡曳力模型基礎上提出大氣泡加速效應，引入大氣泡氣含率修正氣泡群曳力模型。Yang 等[18]基于單氣泡尺寸（SBS）模型提出了雙氣泡尺寸（DBS）模型，DBS 模型可以合理地預測空氣-水系統中發生流態轉變的氣體速度。Yang 等[19]基于雙氣泡尺寸（DBS）模型導出簡化的曳力模型應用于CFD 模擬，DBS 的曳力模型無須調整模型參數即可合理地預測徑向含氣量分布和兩相流場。Qin 等[20]采用了EMMSPBM 的方法對液-液體系的液滴尺徑分布進行了修正，提高了原有模型的準確度。Yang 等[21]率先提出了基于EMMS 方法的群平衡（PBM）模型模擬鼓泡塔內流體行為，模擬結果表明了該模型可以合理地模擬低氣速鼓泡塔中的氣泡粒徑分布。本文在較寬表觀氣速下對漿液鼓泡塔升溫加壓，對Yang 等[19]的曳力模型進行修正，通過CFD-PBM 耦合模型進行數值模擬，并與實驗數據進行對比，以驗證該模型的可行性。

1 數學模型

1.1 雙流體模型

氣液系統模擬采用歐拉-歐拉模型，又稱雙流體模型（TFM）。該模型相對于歐拉-拉格朗日模型與直接模擬，不僅較好地考察了塔內氣含率的分布且大大提高了運算速度。控制方程如下。

質量守恒方程：

動量守恒方恒：

式中，i為氣相g 或液相l；α、ρ、u、t分別為相含率、密度、速度矢量和時間；P為壓力；μeff為流體有效黏度。

1.2 湍流方程

湍流方程模擬了湍動狀態下的氣液系統。本文選擇雷諾時均法（RANS）中的標準k-ε模型[22]，該模型的優點在于適用性廣，計算量較小。方程具體描述如下。

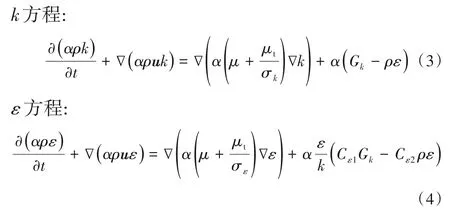
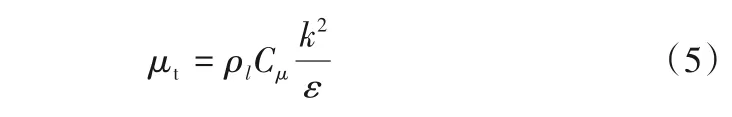
式中，Cε1=1.44,Cε2=1.92,σk=1.0,σ?=1.3。

1.3 相間作用力模型

歐拉-歐拉模型需要相間作用力來封閉，相間作用力的選擇對于模擬結果的精度十分重要。本文模擬選擇了曳力、升力、壁面潤滑力和湍流擴散力，忽略了虛擬質量力的作用。具體表達式如下：

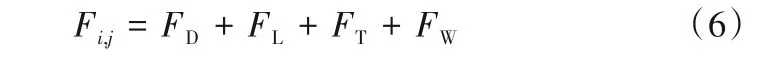
1.3.1 曳力 曳力是一種最主要的相間作用力。本文以Yang 等[19]在常溫常壓空氣-水體系中的雙尺度最小能量化曳力模型為基礎，在加壓加溫的空氣-水體系中，考慮壓力因素的影響，引入密度參數對公式進行了修正；考慮溫度因素的影響，引入黏度和表面張力等參數對公式進行了修正。修正后的公式適用于加溫加壓的空氣-水體系的數值模擬。具體表達式如下：

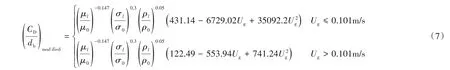
1.3.2 升力 升力是氣泡上升方向垂直的一種作用力。徑向升力對于氣含率的徑向分布至關重要，本文采用的升力表達式如下[23]：

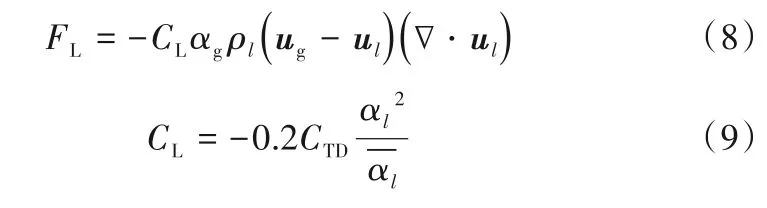
1.3.3 壁面潤滑力 壁面潤滑力是由靠近壁面處氣液速度梯度引起的，是使氣泡遠離鼓泡塔壁面的一種力，本文采用Frank 等[24]的壁面潤滑力，具體表達式如下：

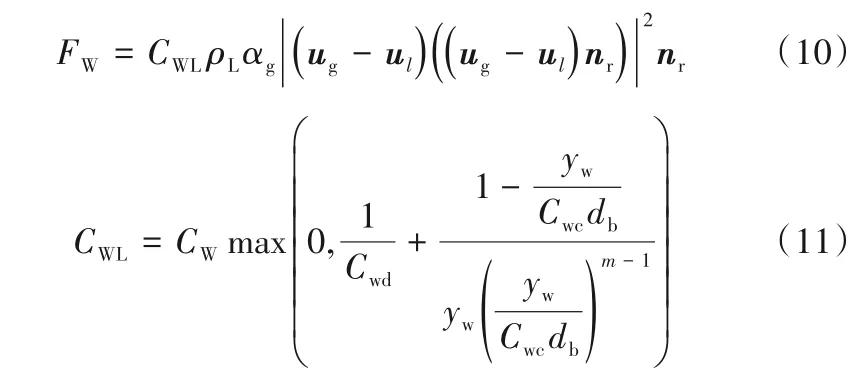
式中，nr為壁面外法向向量；Cwd、Cwc為無量綱常數；m=1.5～2；CW為壁面潤滑力系數，CW是關于Eo的函數，具體表達式如下：

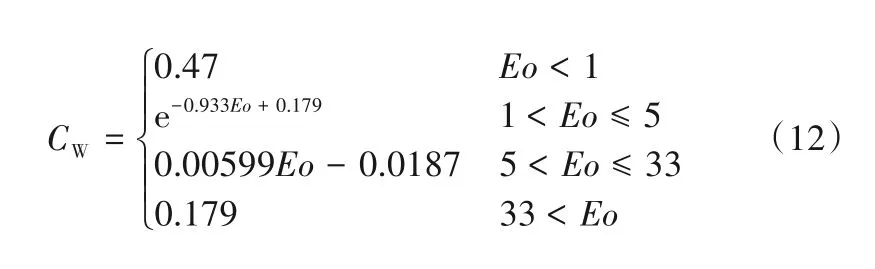
1.3.4 湍流擴散力 湍流擴散力是由液相湍流旋渦引起的，此力使得徑向氣含率分布更均勻。本文采用Lopez de Bertodano[25]的湍流擴散力，具體表達式如下：

式中，kl為湍流強度；CTD為湍流擴散力系數，其取值范圍是0.1～1，本文中取值為1。

1.4 群體平衡模型

群體平衡模型（population balance model，PBM）是描述反應器中顆粒或氣泡大小分布的一種方法。反應器中顆粒或氣泡大小分布對體系的混合、傳質傳熱及反應都有影響。而在鼓泡塔中，氣泡主要發生破碎和聚并，因此該狀況下群體平衡模型表示如式(14)：

式中，V為母氣泡體積；V'為子氣泡體積；n(V',t)為體積為V'的氣泡數密度函數；c(V-V',V')為氣泡聚并速率；β（V,V'）為體積V的氣泡破裂成體積V'的子氣泡分布函數。

1.4.1 破碎模型 氣泡破碎模型主要是由氣泡破碎速率和子氣泡大小分布構成，而引起氣泡破碎的機理主要分為由湍流旋渦與氣泡碰撞引起的破碎、大氣泡由于表面不穩定性引起的破碎。目前應用廣泛的氣泡模型主要以Luo 等[26]和Lehr 等[27]破碎模型為主。本文采用Luo 等的氣泡破碎模型，具體公式如下：

1.4.2 聚并模型 氣泡聚并速率可表示為：

氣泡間碰撞頻率為：

基于Luo 等[28]的聚并效率模型，將改進的聚并系數Ce引入氣泡聚并效率模型中。修改后的聚并模型為：

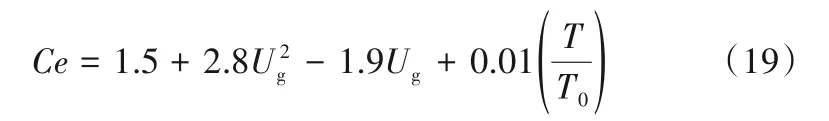
2 加壓加溫實驗

如圖1 所示，鼓泡塔實驗裝置高為1.3 m，內徑為0.1 m，塔底分布器開孔率為1.78%。氣體從壓縮機流出，至壓力儲罐，經轉子流量計、調節閥、分布板進入加壓鼓泡塔，從塔頂流出，經冷凝器、氣液分離器、吸收塔，由截止閥至壓力儲罐，再進入壓縮機，完成一個循環。在鼓泡塔高為0.2、0.3 和0.4 m測量點放置了3個用于測量壓差的壓力傳感器。

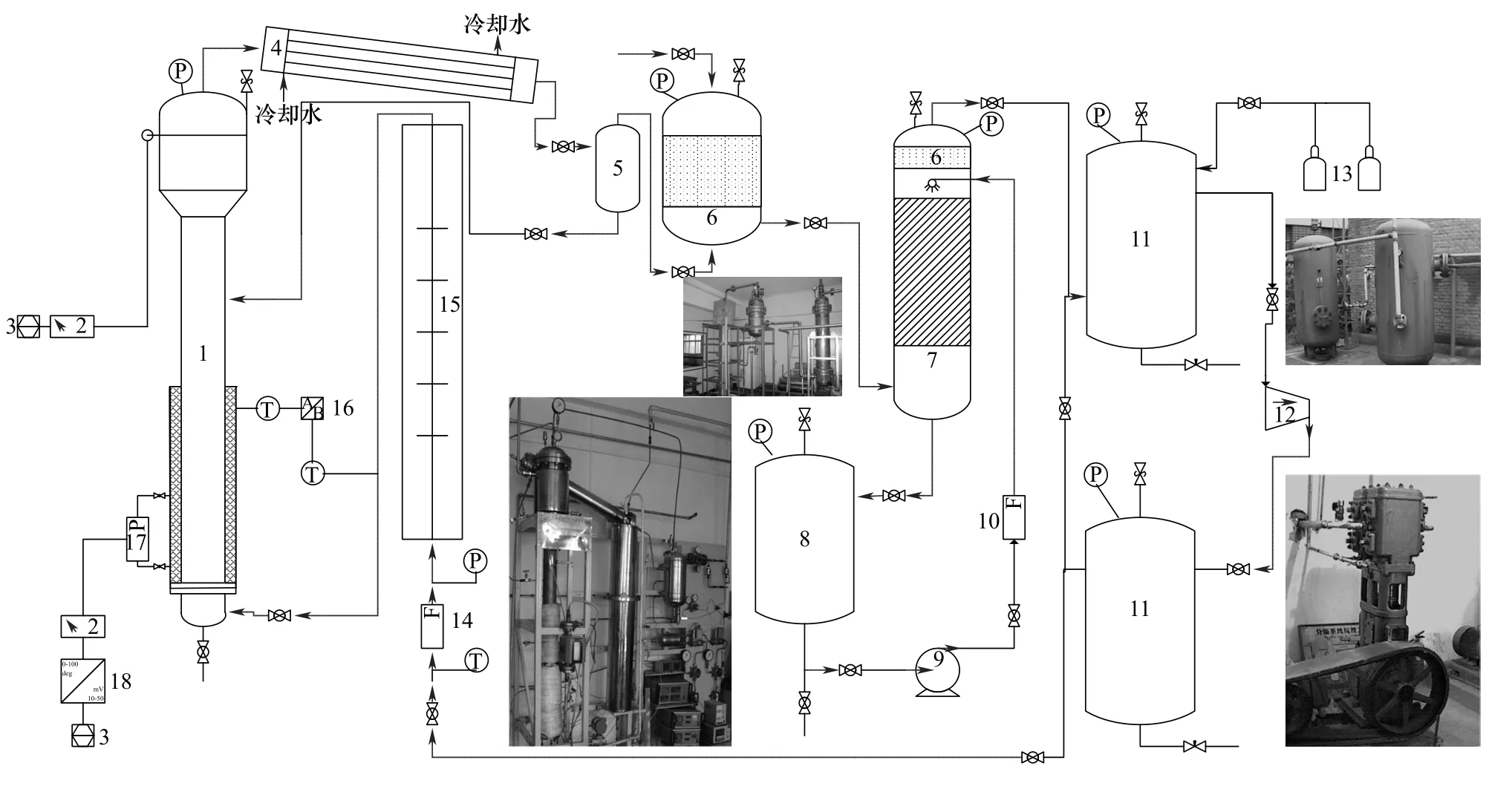
圖1 實驗裝置流程圖Fig.1 Experimental device

3 模型求解方法

本文以FLUENT 15 作為計算平臺，采用非穩態分離求解器求解模型方程。設置速度為入口邊界條件，壓力為出口邊界條件。PBM 模型采用離散方法求解，氣泡大小按照等體積比方法離散為16組子氣泡。模擬的時間步長固定為0.002 s，并認為在60 s內達到了準穩態。當鼓泡塔內的模擬達到穩定后，獲取了塔高為0.3 m 處截面的時間平均徑向氣含率和氣泡直徑分布等數據。該模擬的對象是空氣-水體系，溫度T變化范圍為30～160℃，模擬的壓力為1 MPa，表觀氣速的范圍為0.08～0.24 m/s，塔中靜態高度H0為0.5 m。

3.1 模擬的氣液物性

表1 為氣液兩相的物性，固相為TA（terephthalic acid），TA 的平均粒徑為0.12 mm，密度為1510 kg/m3。從表中可以看出，隨著溫度的升高，液相水黏度降低，表面張力降低。隨著固體濃度增大，漿態水的密度增大，黏度增大，表面張力基本不變。

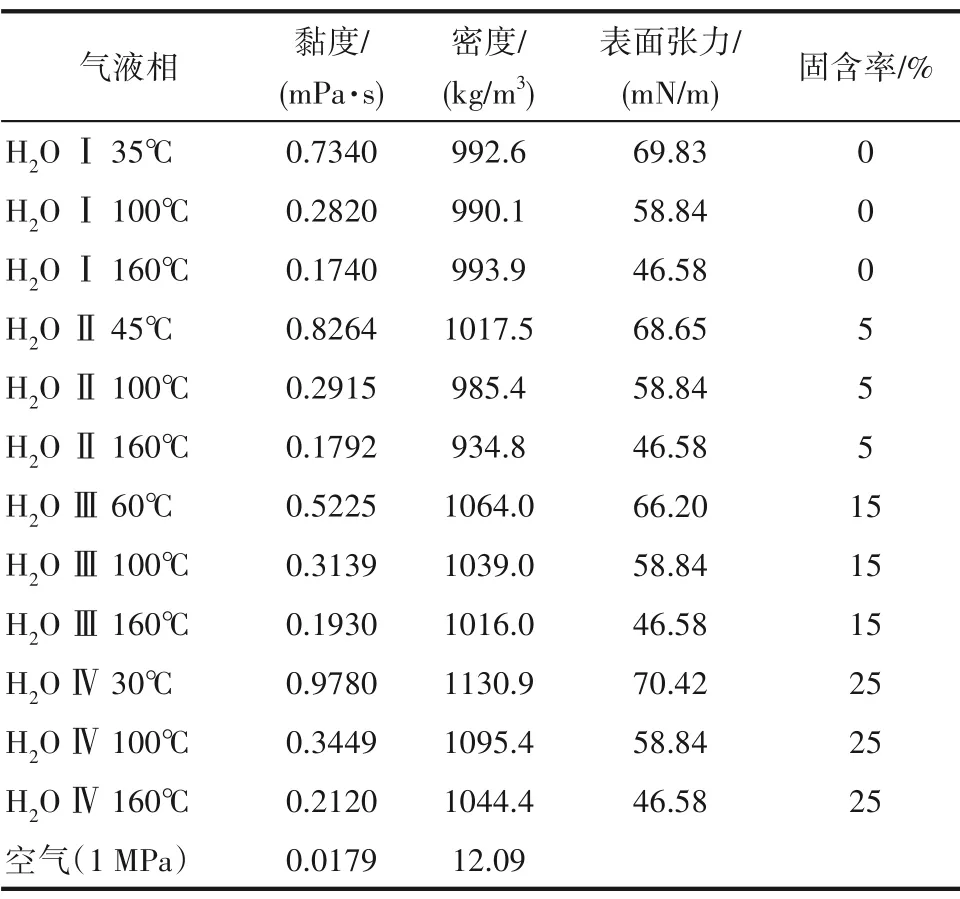
表1 氣液物性Table 1 Physical properties of gas and liquid

3.2 網格無關性驗證

圖2 為三種二維非結構性網格的劃分，其中Grid 1、Grid 2 和Gird 3 三種網格的網格數分別為900、1690 和4160 個。圖3 為35℃下0.08、0.12、0.18和0.24 m/s 四種不同表觀氣速下三種不同質量網格的平均氣含率對比。從圖中可以發現，Grid 1 平均氣含率模擬結果略低于Grid 2 和Gird 3 的模擬結果，而Grid 2 和Gird 3 模擬結果基本接近相同。同時，當網格數量達到一定值后，網格數的增加只會增加計算量，而計算精度沒有提高，因此綜合考慮計算時間和精度的情況下，選擇了Grid 2 中尺寸二維的網格進行模擬。

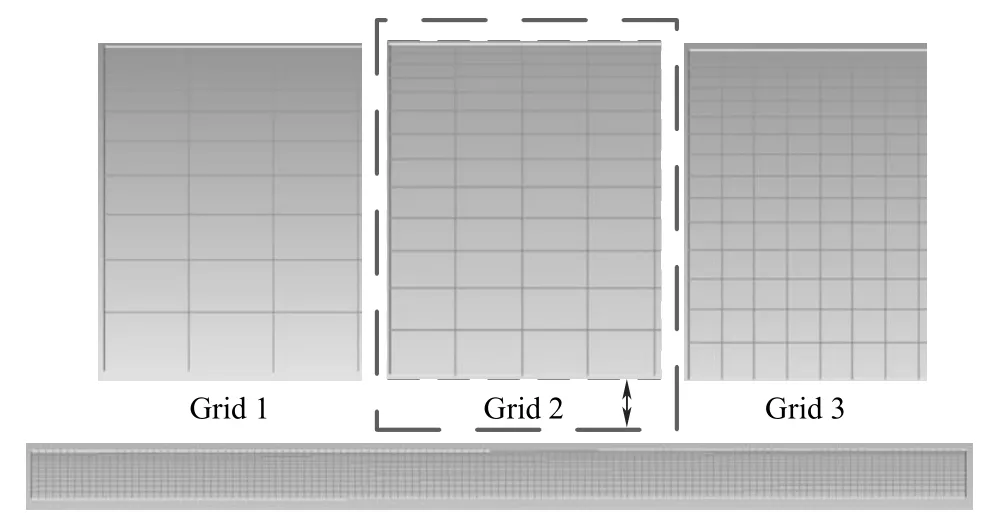
圖2 不同質量網格的劃分Fig.2 Partition of different quality grids

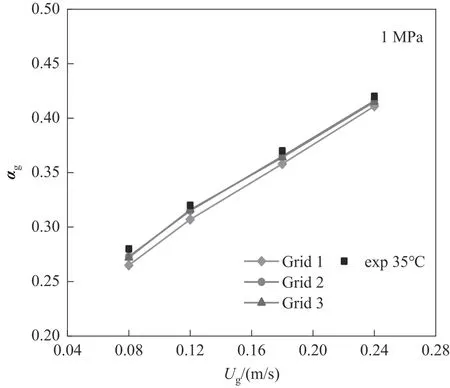
圖3 不同網格質量對平均氣含率的影響Fig.3 The influence of different mesh quality on average gas holdup

4 結果與討論

4.1 表觀氣速對平均氣含率的影響

圖4 為不同溫度下空氣-水體系表觀氣速與平均氣含率的關系。表觀氣速Ug是鼓泡塔中最重要的操作參數之一，決定著流動狀態和相結構組成。因為實驗與模擬的氣速范圍均處于湍流區，在相同溫度下，平均氣含率隨著表觀氣速的增大而單調增加。通過模擬發現，在35、100 和160℃下的模擬結果和實驗值基本吻合，且誤差較小。因此，修正的CFD-PBM 模型在不同溫度和較寬的表觀氣速下可較好地預測相關的流體力學參數。

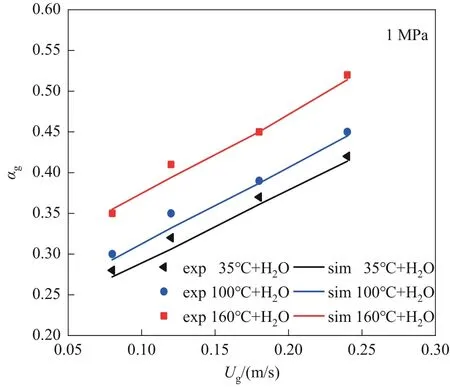
圖4 不同溫度下空氣-水體系表觀氣速與平均氣含率的關系Fig.4 The relationship between superficial gas velocity of airwater system and average gas holdup under different temperatures

4.2 溫度對平均氣含率的影響

圖5 為不同溫度下空氣-水體系溫度與平均氣含率的關系。從圖中可以看出，在相同表觀氣速下，平均氣含率隨溫度的升高而增加，而且溫度越高，平均氣含率增加的幅度也越大。溫度對氣含率的影響要同時考慮液體物理性質的變化和蒸汽壓的變化這兩個因素[29]。塔內溫度較低時，平均氣含率的變化主要受前者的影響；塔內溫度接近水的沸點或者超過水的沸點時，兩種因素都產生影響，但以后者為主。當塔內溫度從35℃升到100℃時，液相水的黏度和表面張力降低，從35℃升到100℃和從100℃升到160℃，水的表面張力和黏度分別下降了16%和62%，在這兩種物理性質中，表面張力的變化對氣含率的影響較大，因為當表面張力降低時，維持氣泡形狀的內聚力減小，這導致大氣泡產生不穩定性，使大氣泡破碎成小氣泡，塔內的平均氣含率增加。平均氣含率在低黏度范圍內隨著黏度的減小而減小，而黏度的變化對氣含率的影響較小。因此，平均氣含率在此溫度范圍內增加。

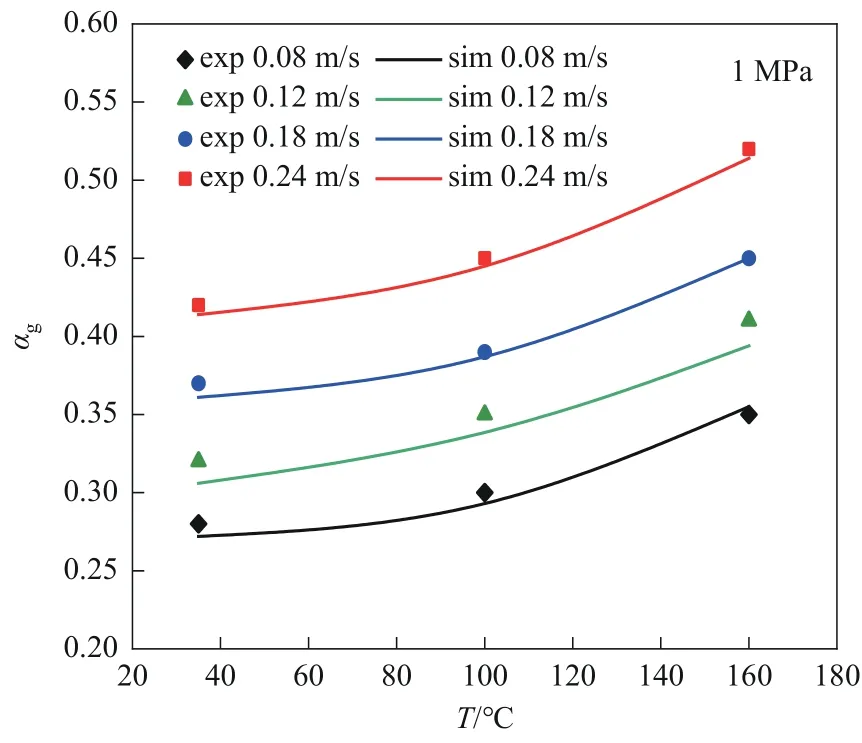
圖5 不同溫度下空氣-水體系溫度與平均氣含率的關系Fig.5 The relationship between temperature of air-water system and average gas holdup under different temperatures

當塔內溫度升高到100℃和160℃時，水的表面張力和黏度分別下降了21%和76%，水的物理性質的變化使得塔內氣含率增加。另外，當溫度超過水的沸點時，塔內液相蒸發，氣相所占比例增大，塔內蒸汽壓增大，也導致平均氣含率增加。這也是在較高溫度下比較低溫度下氣含率增加幅度較大的原因。從圖中還可以看出，模型模擬結果和實驗測量值基本吻合，因實驗僅為平均氣含率數據，下文將采用模擬結果來解釋溫度的變化對流體動力學變化規律的影響。

4.3 固含率對平均氣含率的影響

圖6為不同固含率下空氣-水TA 體系平均氣含率分布。從圖中可以看出，平均氣含率隨著表觀氣速的增加而增加，且表觀氣速越大，平均氣含率增加趨勢越小。因為氣含率的變化趨勢取決于鼓泡塔中流型的變化。在非均勻流動狀態下，由于大氣泡的尾流加速效應，塔中氣泡受到的阻力降低，平均氣含率增加趨勢減小。塔中溫度升高，平均氣含率明顯增加。而且溫度差別越大，平均氣含率增加幅度也越大，在固含率為15%的條件下，溫度從100℃到160℃的氣含率增加量明顯高于溫度從60℃到100℃的氣含率增加量，因為溫度升高，塔內液相水蒸發，塔內蒸汽量增大。因此，塔內溫度越高，平均氣含率增加的幅度越大。在誤差10%范圍內，模型的模擬結果和實驗值基本吻合。

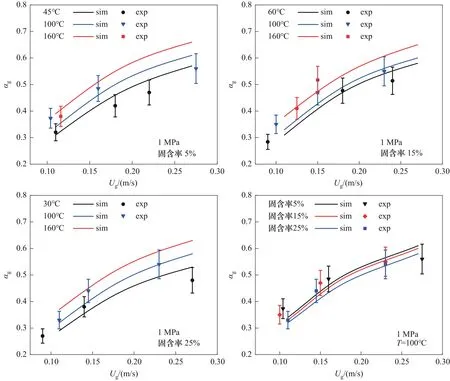
圖6 不同固含率下空氣-水TA體系平均氣含率分布Fig.6 The distribution of average gas holdup of air-water TA system under different solid holdups

在100℃的5%、15%和25%三種不同固含率下，隨著固體濃度的增加，平均氣含率減小，但固含率從5%增加到15%，以及從15%增加25%，平均氣含率變化幅度不大。固體顆粒對氣含率的影響不僅考慮固體濃度，還應考慮顆粒的性質、大小和密度，這些均可能會影響氣含率[30]。隨著塔內固體濃度的增加，漿態水的黏度增加，黏度的增加使得塔內氣泡的聚并增加，塔內的小氣泡減少，氣含率減小。但固含率從5%到25%的變化范圍內，黏度的變化幅度很小，因此平均氣含率也只是略微減小。實驗值和模擬結果在10% 的誤差范圍內基本吻合。

4.4 空氣-水體系大小氣泡氣含率

圖7 為35、100 和160℃三種不同溫度下，表觀氣速對總氣含率、大氣泡氣含率和小氣泡氣含率的影響。在本文的模擬中，使用Ishii 等[31]的相關式來區分小氣泡和大氣泡，即dc=4[σ/g(ρl-ρg)]。從圖中可以看出，隨著表觀氣速的增大，總氣含率、大氣泡氣含率及小氣泡氣含率都有相應程度增加。但隨著表觀氣速的增大，大氣泡氣含率增加的幅度大于小氣泡的，這也與Zhang 等[8]的研究結果一致。產生這種結果的原因是隨著塔內表觀氣速的增大，增加了塔內氣泡的聚并，大氣泡數量增多，這使得大氣泡的氣含率增加幅度較大。

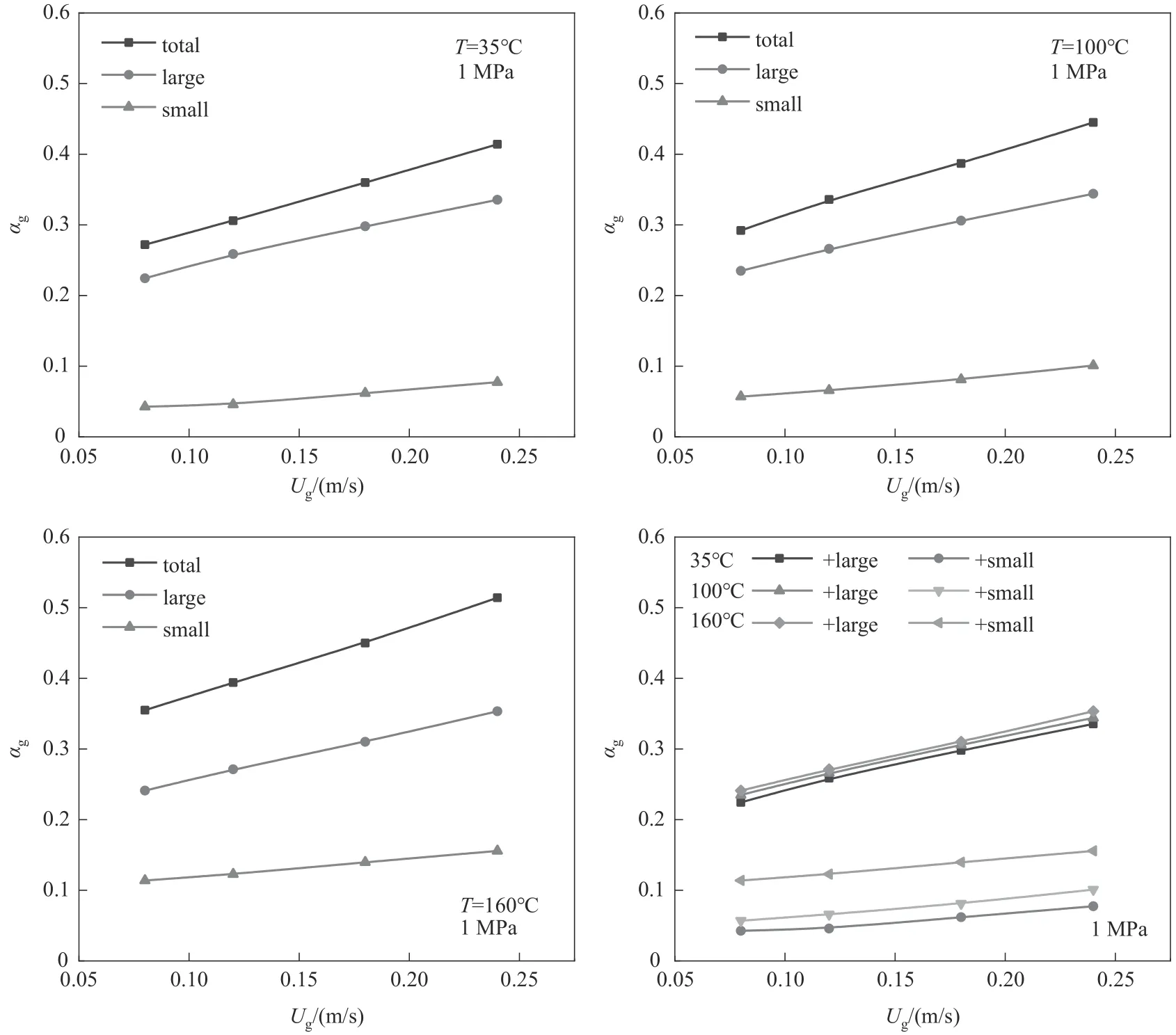
圖7 不同溫度下空氣-水體系溫度與大小氣泡氣含率的關系Fig.7 The relationship between temperature of the air-water system and large and small bubbles gas holdup under different temperatures

在相同表觀氣速下，隨著塔內溫度的升高，總氣含率明顯增加，這是因為隨著溫度的升高，液相水的表面張力和黏度減小，這兩種液體性質中表面張力影響尤為突出，表面張力減小使得氣泡的穩定性變弱，這導致大氣泡破碎成小氣泡，使得塔內的總氣含率增加。塔內小氣泡數密度的增加，使得小氣泡的氣含率較大程度增加，大氣泡氣含率略微增加。

4.5 空氣-水TA體系大小氣泡氣含率

圖8 為100℃下不同固含率空氣-水TA 體系大小氣泡氣含率的關系。從圖中可以看出，隨著固含率的增加，總氣含率減小，大氣泡氣含率略微增加，小氣泡氣含率減小。這是因為隨著TA 固體含量的增加，增加了塔內氣泡聚并行為的發生，并且抑制了塔內氣泡的破碎，塔內小氣泡的數量減少，使得塔內小氣泡氣含率減小。隨著TA 固體含量的增加，塔內總氣含率減小，因此大氣泡氣含率增加的幅度小于小氣泡氣含率減小的幅度。

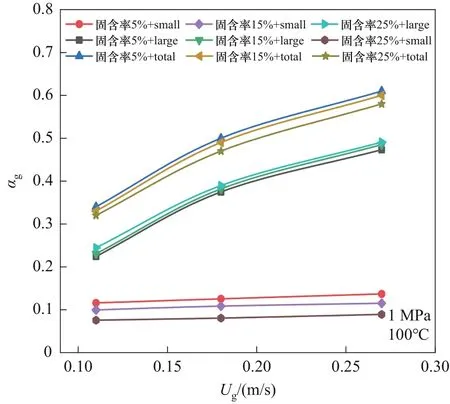
圖8 不同固含率下空氣-水TA體系大小氣泡氣含率的關系Fig.8 The relationship of large-bubble and small-bubble gas holdup of air-water TA system with different solid holdups

4.6 空氣-水體系徑向氣含率分布

圖9 為不同溫度下空氣-水體系的徑向氣含率分布。從圖中可以看出，徑向氣含率從塔中心到塔壁處逐漸減小。在相同溫度下，徑向氣含率隨表觀氣速的增大而增加；相同表觀氣速下，徑向氣含率隨溫度的升高而增加，這與平均氣含率隨溫度升高的變化規律一致。并且隨著溫度的升高，徑向氣含率變化趨勢越來越平緩。Chabot 等[32]研究表明溫度升高改善了氣泡徑向分布的均勻性，導致徑向氣含率變化趨勢更加均勻，增大了塔內的氣含率。

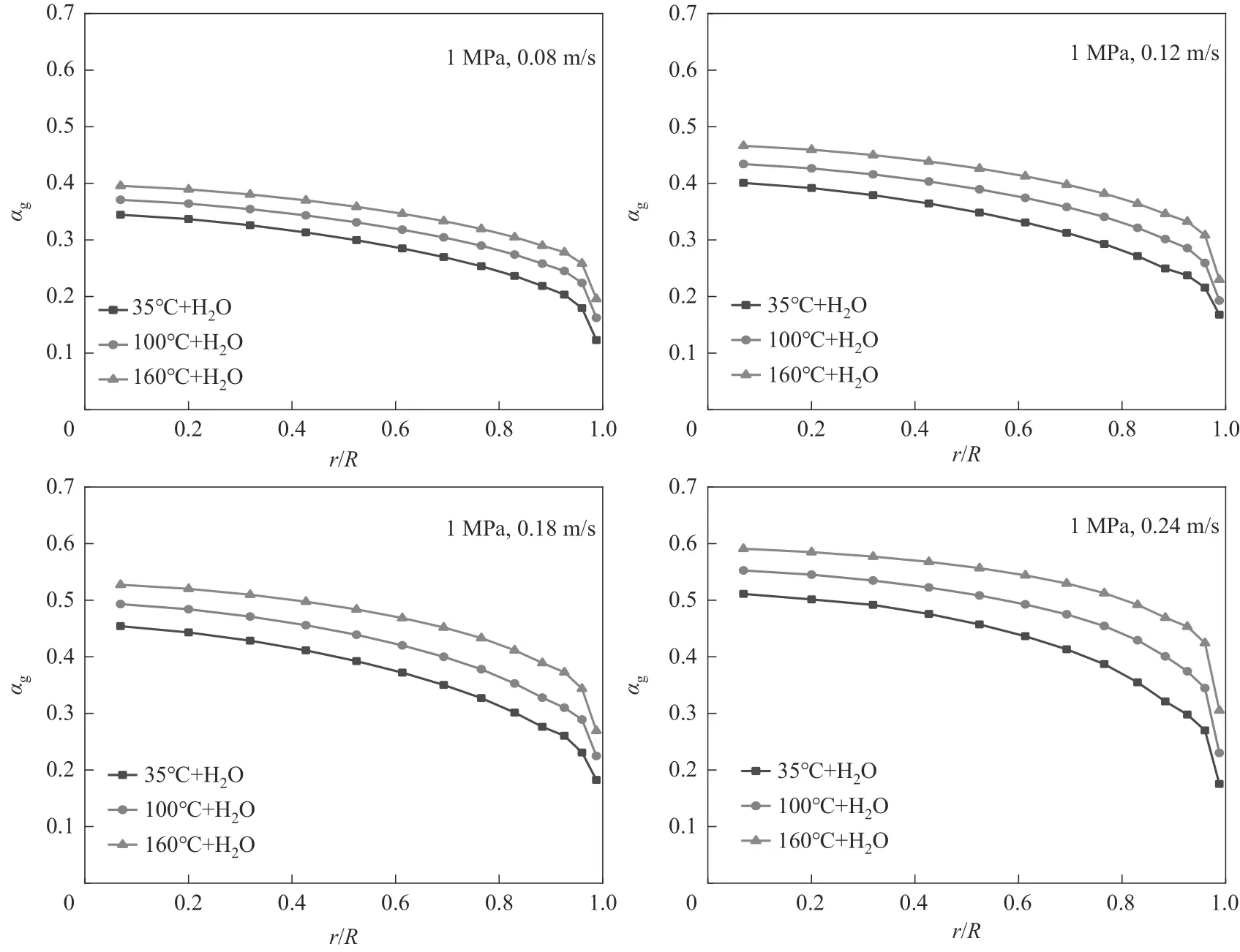
圖9 不同溫度下空氣-水體系的徑向氣含率分布Fig.9 Radial gas holdup distribution diagram of air-water system at different temperatures

4.7 空氣-水體系軸向截面氣含率云圖分布

圖10為不同溫度和表觀氣速下空氣-水體系軸向對稱截面氣含率云圖分布。圖10（a）為35℃下，不同表觀氣速的氣含率云圖分布；圖10（b）為0.12 m/s 的表觀氣速下，不同溫度的氣含率云圖分布。不同云圖左側邊為塔的中心對稱軸，右側邊為塔的壁面。從圖中可以看出，氣含率在塔中心較大，壁面處較小，而且氣含率隨表觀氣速和溫度的升高而增加，其變化規律和徑向氣含率變化規律相同。但是從軸向氣含率云圖分布可以看出氣含率的變化趨勢。隨著溫度和表觀氣速的增加，塔中的液面也隨之升高，且在鼓泡塔中充分發展區域，氣含率的大小分布基本一致。李兆奇[33]通過對列管型鼓泡塔中流動發展規律的研究認為，在鼓泡塔充分發展階段，氣含率不會受到塔高變化的影響。這與本部分的研究結果相同。

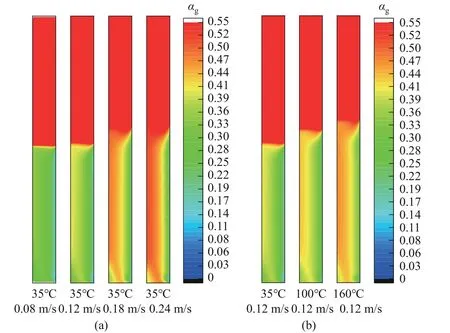
圖10 空氣-水體系軸向截面氣含率云圖分布Fig.10 Distribution diagram of air holdup contours in axial section of air-water system

4.8 空氣-水體系軸向液速分布

圖11 為不同溫度和表觀氣速下軸向液速分布。從圖中可以看出，軸向液速從塔中心到塔壁處逐漸減小，在r/R約為0.7 的近塔壁處軸向液速呈現向下的趨勢（出現了負值）。在相同的溫度下，軸向液速隨表觀氣速的增大而增大，這是因為軸向向上的氣速對塔內液體施加了向上的作用力，且表觀氣速越大，所施加的作用力越大，軸向液速越大；在相同表觀氣速下，隨著塔內溫度的升高，軸向液速基本沒變化，這是因為隨著溫度的升高，只改變了液體的表面張力和黏度等物理性質。只有物理性質發生變化，并不會引起塔內軸向液速的變化。

圖11 不同溫度下空氣-水體系軸向液速分布Fig.11 Radial distribution of liquid velocity at different temperatures

4.9 空氣-水體系氣泡直徑分布

圖12 為不同溫度下空氣-水體系氣泡直徑分布。從圖中可以看出，在相同溫度下，隨著表觀氣速的增加，氣泡直徑增大。這是因為隨著表觀氣速增加，塔內氣泡聚并的概率增大，小氣泡聚并形成大氣泡，進而導致塔內大氣泡變多，使得塔內氣泡尺寸變大。在相同表觀氣速下，隨著塔內溫度的升高，氣泡直徑呈現出減小的趨勢。這是因為隨著塔內溫度升高，水的表面張力減小，這使得維持氣泡形狀的內聚力減小，大氣泡穩定性減弱，使大氣泡破碎成小氣泡；同時溫度超過水的沸點時，液相水大量蒸發成蒸汽，體系內蒸汽壓增大，也有利于大氣泡破碎形成小氣泡，使得塔內氣泡直徑有減小的趨勢。

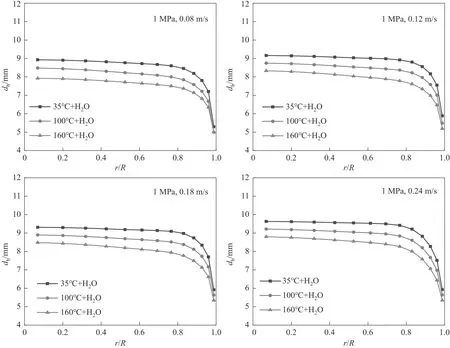
圖12 不同溫度下空氣-水體系氣泡直徑分布Fig.12 The bubble diameter distribution diagram of air-water system at different temperatures

4.10 空氣-水體系氣泡數密度分布

圖13為不同溫度下空氣-水體系溫度與氣泡數密度分布的關系。從圖中可以看出，氣泡尺寸為7～8 mm 的氣泡數量最多。在相同溫度下，隨著表觀氣速的增加，大氣泡數量相對增多，小氣泡數量相對減少，子氣泡分布范圍變寬。這是因為隨著表觀氣速的增加，塔內氣泡聚并的概率增大，使得小氣泡聚并成大氣泡，氣泡分布范圍變寬。在相同表觀氣速下，隨著溫度的升高，塔內液相的表面張力減小，蒸汽壓增大。液相表面張力的減小使得維持氣泡形狀的內聚力減小，有利于塔內大氣泡破碎成小氣泡；蒸汽壓的增大，使得氣泡攜帶的能量增加，增大了氣泡與氣泡和氣泡與湍流旋渦的碰撞概率，小氣泡數量增多，小氣泡分布范圍變窄。

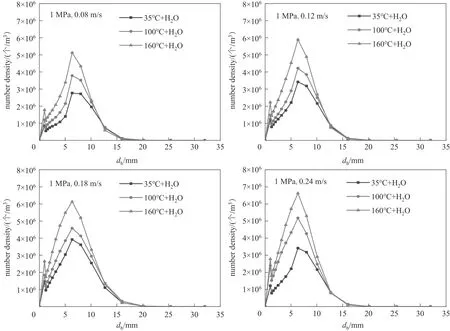
圖13 不同溫度下空氣-水體系溫度與氣泡數密度分布的關系Fig.13 The relationship between temperature of air-water system and bubble number density distribution under different temperatures

5 結論

本文通過對加壓加溫鼓泡塔中空氣-水體系氣-液兩相流的CFD-PBM耦合數值模擬，研究了溫度對鼓泡塔中流體力學行為的影響，具體結論如下。

（1）在加溫加壓鼓泡塔內，通過對35、100 和160℃三個溫度下的數值模擬，結果表明，表觀氣速增大，平均氣含率增加；固含率增加，平均氣含率減小；溫度升高，平均氣含率增加，且平均氣含率在溫度越高的情況下增加幅度越大。這是因為溫度升高，液相水表面張力的減小和塔內蒸汽壓的增大導致大氣泡破碎成小氣泡，平均氣含率增加。而且通過模擬發現,平均氣含率的模擬結果和實驗值在10%的誤差范圍內吻合較好。

（2）塔內表觀氣速增大，空氣-水體系的總氣含率、大氣泡氣含率及小氣泡氣含率都有相應程度的增加，但大氣泡氣含率增加的幅度大于小氣泡的。固含率增加，總氣含率減小，小氣泡氣含率減小；溫度升高，總氣含率明顯增加，小氣泡的氣含率有較大程度增加，大氣泡氣含率略微增加。這是因為溫度升高，液相水表面張力的減小和塔內蒸汽壓的增大導致大氣泡破碎成小氣泡。因此，總氣含率和小氣泡氣含率都增加。

（3）塔內表觀氣速增大，氣泡尺寸變大；溫度升高，氣泡尺寸變小。在相同溫度下，表觀氣速增加，氣泡聚并行為增強，大氣泡數量相對增加，子氣泡分布范圍變寬；但在相同表觀氣速下，溫度的升高，液相水表面張力的減小和塔內蒸汽壓的增大導致大氣泡破碎成小氣泡，氣泡數密度增加，子氣泡分布范圍相對變窄。

符號說明

b（fv,d）——尺寸為d的氣泡破碎速率

CD——曳力系數

CL——升力系數

CTD——湍流擴散力系數

Ce——聚并系數

D——鼓泡塔內徑，m

db——氣泡直徑，mm

Eo——E?tv?s數

fv——破碎速率

H——鼓泡塔高度，m

H0——靜液面高度，m

r/R——徑向位置

T——液體溫度，℃

Ug——表觀氣速，m/s

ul——軸向液速，m/s

αg——平均氣含率

?——湍流耗散率，m2/s3

ζ——氣泡相對直徑

ζmin——氣泡最小相對直徑

μl——液體黏度，Pa·s

ρl——液體密度，kg/m3

σl——液體表面張力，N/m

?（cdi,d）j——尺寸為di和dj的氣泡間的碰撞頻率，m3/s

下角標

b——氣泡

eff——有效