基于DEM 模擬的顆粒材料熱固結試驗分析*

應濤濤，魏良針，楊 磊，夏念興，龔禮岳

（1.溫州市鐵路與軌道交通投資集團有限公司，浙江 溫州 325000；2.溫州大學 建筑工程學院，浙江 溫州 325000）

基于節能環保可持續的發展原則，如能源樁[1]和地源熱泵[2]等與溫度相關的能源工程[3-5]開展得越來越多，溫度對能源結構周邊土體的影響已經成為工程在使用過程中不可忽略的重要因素。Sang 等[6]分別在室內和高溫下進行了飽和粘土的熱排水固結試驗，發現溫度可以加快排水固結的固結速度。Xiong 等[7]開發了一種溫度控制的三軸試驗裝置，研究了飽和軟粉質粘土在不同溫度下的動態不排水特征，發現溫度對軟粘土的累積塑性變形、孔隙水壓力等特性有很大的影響。此外，溫度土體的強度[8-10]、空隙特征[11]、變形[12]等特性也有較大的影響。土體特性的改變必然會造成土體與結構接觸面特性的變化。Maghsoodi 等[13]建立了非等溫土-結構界面模型，討論了溫度對粘土-結構界面空隙率的影響。Donna 等[14]開發了一種直接剪切裝置，研究了不同溫度下樁-土界面的響應，發現粘土-混凝土界面的強度隨溫度的升高而增加。此外，研究還表明溫度對土-結構界面的接觸力[15]、應力-應變[16]和抗剪強度[17-19]等特性都有影響。而土-結構接觸面特性的變化勢必會引起結構的不均勻沉降甚至失穩，所以需進一步深入土體的溫度效應的研究。但是，上述試驗中都只是分析了溫度對土體在宏觀上的如強度、應力和應變等影響，缺少了如各項異性、內部接觸力分布等微觀層面的研究。

離散元法[20]（DEM）作為一種能應用于工程領域的數值計算方法，將巖體視為不連續的離散塊體能有效地進行顆粒接觸間的微觀模擬。Pan 等[21]通過離散元模擬了粗粒土的熱誘導變形，發現粗粒土在加熱時發生膨脹，在冷卻時發生收縮，且收縮的幅度大于膨脹的幅度；同時還發現了由于顆粒間的滑動，顆粒重排的增加。Coulibaly 等[22]通過離散元法對粒狀材料進行了熱循環的模擬，發現了溫度循環對顆粒材料的結構和性能都有顯著的影響。Zhao 等[23]則發現熱循環在粒狀材料內部會引起顯著的應力松弛。但是，目前離散元法進行的熱力耦合模擬大多采用的是顆粒體體積膨脹法，較少對真實傳熱過程的模擬。

所以，本文分別采用熱傳遞法和顆粒體積膨脹法，通過離散元軟件PFC2D來模擬單次溫度循環下的熱固結實驗。宏觀上分析試樣密實化和應力衰減的規律，在微觀方面研究了顆粒間接觸的各項異性受溫度的影響規律，最后對比分析了兩種模擬方法在模擬過程中的同異性。

1 熱力耦合模型的機理

1.1 顆粒體積膨脹法

顆粒體積膨脹法是指不考慮顆粒間的熱能傳遞，顆粒溫度的變化直接通過參數的設置來實現。在模擬過程中，通過公式（1）實現溫度對顆粒體積的影響。

式中，ΔT 是顆粒溫度的變化量；α 是顆粒的熱膨脹系數；R0是顆粒變溫前的半徑；ΔR 是顆粒在變溫時產生的半徑的變化量。

顆粒體積的改變使顆粒間接觸的重疊量δn隨之發生變化，然后通過接觸力的計算公式（2）實現熱力耦合的模擬。

在采用顆粒體積膨脹法的溫度固結試驗模擬過程中，全部顆粒的溫度都是相同的，且都是統一發生變化的。由于不需要考慮溫度的傳遞，采用顆粒體積膨脹法的熱力耦合在PFC2D軟件上的模擬更加快速。因此在進行如溫度循環試驗這類溫度需要長期持續變化的模擬中顆粒體積膨脹法的運用是必不可少的。

1.2 熱傳遞法

在采用熱傳遞法的熱力耦合模型中，每一個顆粒都代表一個蓄熱池。在兩個蓄熱池顆粒互相接觸后，中心會形成一根連接這兩個蓄熱池的傳熱管道簡稱熱管。通過熱管就可以實現熱能在兩個蓄熱池之間的轉移。

在模擬過程中，將邊界墻體作為恒定的熱源對內部的顆粒進行熱能的供應。且邊界墻體不隨溫度的變化而產生變形。在傳熱過程中，邊界墻體的熱能會從較近的顆粒向較遠的顆粒傳輸。而顆粒的溫度在邊界熱能的作用下會不斷升高直到與邊界墻體的溫度相同。與此同時，在顆粒溫度升高的過程中，顆粒體積則會根據公式（1）產生膨脹。并通過公式（2）實現溫度對試樣力學性質的影響。

通過熱傳遞法進行的熱力耦合模擬更加接近現實中能源結構對周邊土體的影響。但是由于其在模擬過程中需要兼顧熱傳遞和力學計算，會導致模擬速度的降低，不利于開展如多周期溫度循環固結試驗等有長時間傳熱試驗的模擬。

2 模型的建立及模擬方案

2.1 數值模型的建立

圖1 為試樣模型的顆粒粒徑分布曲線，曲線中的相關數據見表1。按照這一級配曲線，生成相對密實度Dr為0.2 的松散試樣其對應的孔隙比為0.2376。

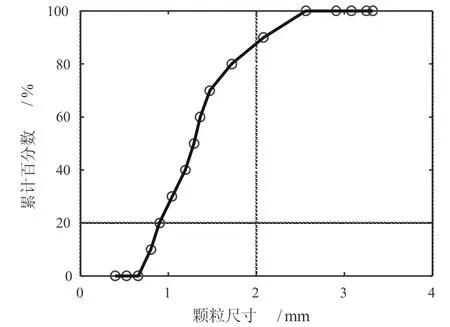
圖1 顆粒級配曲線

模型中力學參數和熱力學參數的選取主要參考石英砂的數值如表2 所示。

在顆粒生成后，循環計算至試樣內部平均不平衡系數αf（見公式（3））小于1e-5。將平衡后的試樣進行側限壓縮固結。在固結過程中的邊界條件為在上下墻體施加100kPa 的恒定荷載，左右墻體保持靜止不動。在后續的溫度固結試驗過程中會保持這個邊界條件不變。側向固結后的試樣如圖2 所示，此時試樣的孔隙比e0為0.2312，將此狀態下的試樣視為溫度固結試驗中的初始狀態。

圖2 數值試樣模型

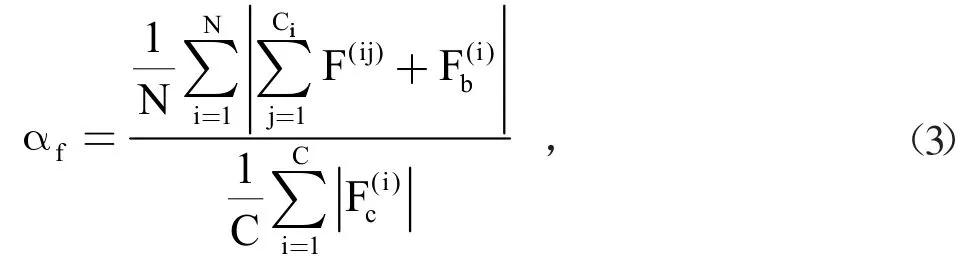
式中N 是顆粒的總數；C 是總的接觸數量；Ci是第i 個顆粒的接觸數量；F(ij)是第i 個顆粒的第j 個接觸的接觸力；Fb(i)是第i 個顆粒的體積力；Fc(i)是第i 個接觸的接觸力。

2.2 模擬方案

分別采用熱傳遞法和顆粒體積膨脹法進行溫度固結試驗的模擬。在模擬過程中，設置顆粒的初始溫度T0為20℃，溫度變化過程為20℃～60℃～20℃。

在熱傳遞法中，先將邊界墻體的溫度設置為60℃并保持溫度固定，在試樣的平均溫度升高到60℃后再將邊界墻體的溫度改為20℃，使試樣的平均溫度重新降低到20℃，以此實現溫度循環固結試驗的模擬。

在顆粒體積膨脹法中，以固定的溫度增量ΔT=1℃進行顆粒溫度的設置。試樣平均溫度具體的變化過程為20℃～21℃～22℃～......～60℃～59℃～58℃～......～20℃，如圖3所示。

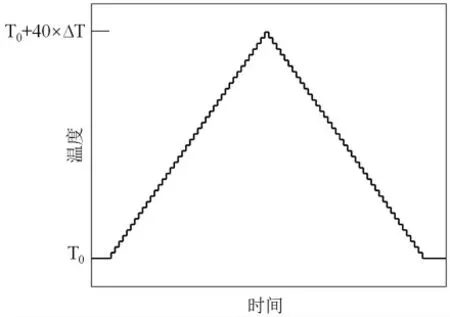
圖3 溫度變化示意圖

最后，將兩種熱力耦合方法的模擬數據在宏觀角度（孔隙比、側向應力）和微觀角度（各項異性）上進行對比分析。

3 試驗結果

3.1 孔隙比及側向應力

為方便在數據圖中進行標注，將熱傳遞法簡稱為方法Ⅰ，將顆粒體積膨脹法簡稱為方法Ⅱ。圖4 為兩種方法下的孔隙比在溫度循環固結模擬下的對比結果。當溫度從20℃升高到60℃時，兩種方法分別從初始孔隙比0.23122降低到了0.23082 和0.23081，當溫度從60℃降低到20℃時，孔隙比又分別升高到了0.23114 和0.23117。可以看出，在經過一次溫度循環后，試樣的孔隙比相較于初始狀態時是降低的。這是由于在恒定的邊界條件作用下，溫度的升高使顆粒的體積不斷膨脹降低了試樣的孔隙比，而溫度的降低使顆粒體積逐漸收縮，導致試樣孔隙比的增加，顆粒體積在不斷變化過程中產生了塑性變形，使試樣體積無法還原到初始狀態。這種孔隙比的變化規律與Liu 等[30]關于不同溫度下的孔隙率變化規律相同。同時也可以看出，兩種熱力耦合方法在孔隙比上的變化是高度吻合的。

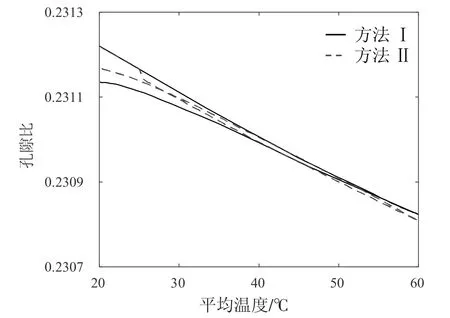
圖4 孔隙比在溫度循環過程中的變化

由于在邊界條件中上下墻體施加了恒定的荷載，試樣在豎直方向上的應力是恒定的，因此對于應力的研究主要針對側向應力。圖5 為試樣的側向應力在熱固結試驗模擬中的變化情況。隨著溫度的升高，側向應力從初始應力41.54kPa 分別增加到了48.34kPa 和48.11kPa。隨著溫度的降低，側向應力也隨之降低到了40.44kPa 和40.59kPa。這也是由于側向墻體對試樣的約束力會隨著顆粒體積的膨脹而增加，隨著顆粒體積的收縮而降低的原因造成的。此外，可以看出模型Ⅰ與模型Ⅱ的側向應力曲線十分相近的。

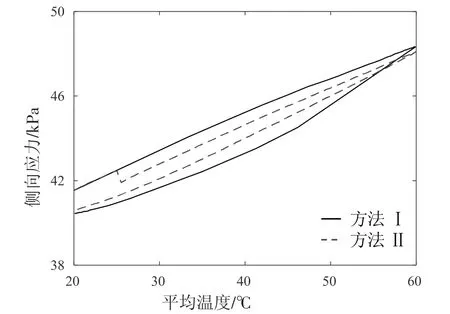
圖5 溫度循環過程中側圍壓力的變化

3.2 各項異性

參考Rothenburg 和Bathurst[31]關于各向異性的擬合公式（4）分別從法向接觸力和切向接觸力兩個方面對比方法Ⅰ和方法Ⅱ對試樣的影響。

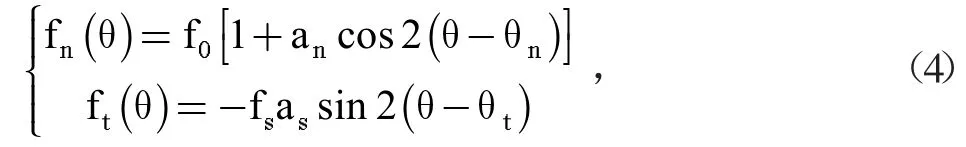
式中：fn和ft分別為法向接觸力和切向接觸力在θ（θ∈[0，2π]）角度上的大小；f0和fs為法向接觸力和切向接觸力的平均值；an和as分別表示了法向接觸力和切向接觸力的方向變化量，其數值越大，接觸力的各向異性就越明顯，由公式（5）計算所得；θn為最大平均法向接觸力的傾角；θt為平均切應力為零時的傾角。

式中：E（θ）為接觸密度函數；ai表示分布的各向異性大小；θi表示i 對應的各向異性方向，其中i 分別為n 和t。

圖6 為溫度固結試驗模擬中平均法向接觸力隨溫度的變化曲線。當溫度從20℃升高到60℃時，方法Ⅰ和方法Ⅱ的f0從65.26kN 分別增加到了69.86kN 和70.06kN。當試樣的溫度重新降低到20℃時，f0又分別降低到了65.02kN 和65.05kN。相較于初始狀態分別降低了0.24kN和0.21kN。

為了進一步觀察法向接觸力在試樣內部的分布情況，分別取平均溫度為60℃和完成溫度循環后（平均溫度為20℃）的試樣進行分析，如圖7 所示。當平均溫度分別為60℃和20℃時，法向接觸力在水平方向上的分布分別約為64.72kN 和52.51kN，在豎直方向上的分布則因為穩定的邊界條件保持在76.49kN 左右。當試樣的平均溫度重新降低到20℃時，由于法向接觸力在水平方向上的分布降低，使其整體處于降低的趨勢，與圖6 中的變化趨勢相同。此外，可以看出，熱傳遞法和顆粒體積膨脹法在相同溫度下的法向接觸力的分布高度吻合。

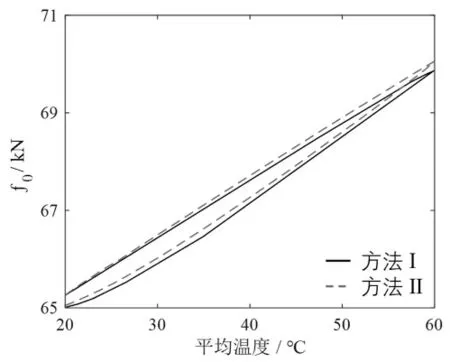
圖6 平均法向接觸力隨溫度的變化

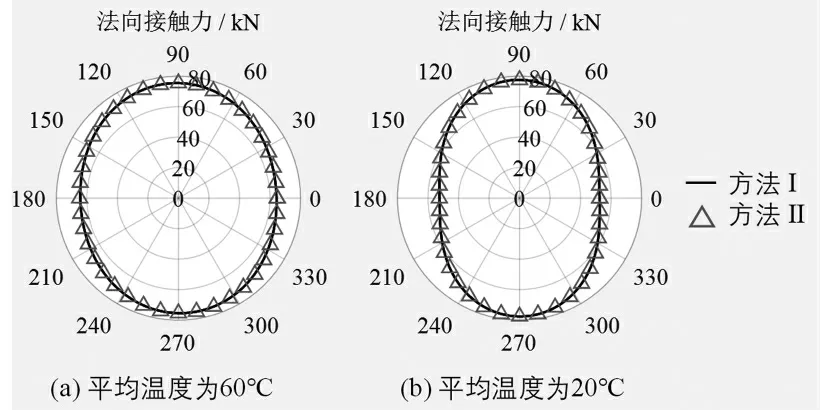
圖7 法向接觸力分布示意圖

圖8 為平均切向接觸力fs在熱固結試驗模擬中的變化曲線。從圖中可以看出，隨著溫度的升高，兩種方法的平均切向接觸力fs從初始的1.735kN 分別降低到了0.637kN 和0.631kN。隨著溫度的降低，fs分別增加到了1.883kN 和1.855kN。相較于初始狀態，經過溫度循環后的試樣的切向接觸力是有所增加的。

圖8 平均切向接觸力隨溫度的變化

如圖9 所示，分析了切向接觸力在平均溫度分別為20℃和60℃時的分布。當試樣的平均溫度從60℃降低到20℃時，切向接觸力在方向上分布的最大值從0.4635kN增加到了2.837kN，變化情況與圖8 中的曲線相吻合。同時，當平均溫度為60℃時，方法Ⅰ和方法Ⅱ的切向接觸力方向上的最大值分別為0.4635kN 和0.4237kN，其差異可以忽略不計。因此，兩種方法在切向接觸力的分布上也有高度的相似性。

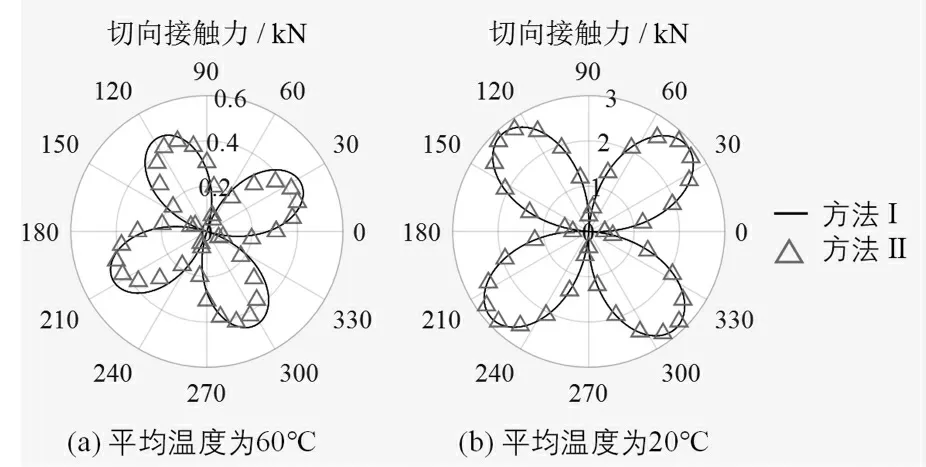
圖9 平均切向接觸力分布示意圖

4 結論

為了進一步研究在能源樁的使用過程中，樁身溫度的變化對其周邊土體的影響。本文通過PFC2D軟件，利用離散元法（DEM），分別采用熱傳遞法和顆粒體積膨脹法對石英砂材料進行了熱固結試驗的模擬。分別從宏觀角度和微觀角度分析了結構接觸面周圍土壤的熱耦合力學性能。并對比分析了兩種熱力耦合方法的模擬情況。得到以下結論：

（1）通過PFC2D軟件，利用離散元法，無論是基于熱傳遞法還是顆粒體積膨脹法，都能很好地實現溫度固結試驗的模擬，在模擬過程中，能夠明顯地體現出溫度對顆粒體積的影響。

（2）在宏觀角度上，在上下墻體施加穩定100kPa 的荷載，左右墻體保持固定的邊界下，在溫度循環固結試驗模擬中，顆粒體積產生塑性變形導致孔隙比的降低，試樣變化更加密實；因此也導致了試樣側向應力的降低。

（3）在微觀角度上，由于在水平方向的分布隨側向應力的降低而降低，法向接觸力在經過溫度循環后是降低的。與之完全相反的是平均切向接觸力是增加的。

（4）熱傳遞法和顆粒體積膨脹法在循環的熱固結試驗中的模擬結果無論是在宏觀方面還是在微觀方面，都具有高度的一致性。

以上研究結果可為能源樁周土的研究提供參考依據。