各向異性滲透性對快速下降土壩邊坡穩定性分析的影響

張懷永

（安徽三洲水利建設有限公司,安徽 宿州 234000）

1 引言

大壩的快速下降現象,庫水位的降低改變了壩坡所承受的應力,也影響了內部孔隙水壓力。巖土材料內部的孔隙壓力會受多種因素影響。郭麗娜等[1]通過有限元模擬了地震對大壩孔隙水壓力的影響,得出震后超孔隙水壓值隨時間減小,滲透系數越小,超孔隙水壓力消散越慢。超孔隙水壓最大值一般在上游反濾層頂部出現。多余孔隙水壓力隨時間消散,會導致邊坡沉降,吳勇等[2]考慮了動水作用下的堤防邊坡流固耦合滲流問題,從而引起邊坡沉降。整個滲流過程受水流速度及原位土壤性質等多因素影響。

戚海棠等[3]考慮了兩種土質及各向異性程度和各向異性方向,對庫區水位下降的滲流、變形及穩定性進行了數值模擬。楊建民等[4]用有效應力形式來分析土坡的穩定性,從而得出穩定安全系數值。達明昌等[5]研究了庫水位變動和降雨共同作用對心墻壩上下游壩坡穩定性的影響,考慮了滲流場和應力場的耦合。

在上述討論的背景下,可以觀察到,目前大多數的水位下降分析都假設各個方向的滲透率是一致的。然而,多孔介質在本質上是各向異性的。因此,假設土壤的各向異性對超孔隙壓力的消散以及對水位下降期間上游殼體的破壞有重大影響。因此,本文主要了解各向異性滲透性對水位下降引起的邊坡穩定性的影響。本研究假設水平滲透率（kx）值是通過CPT耗散試驗以合理的精度估算的,各向異性的影響在垂直方向上進行,即ky=kx/n,其中n在1.5 ~4.0 之間。在此基礎上,綜合分析坡角、降深率、庫水位等參數對邊坡降深過程中穩定性的影響。

2 材料特性

分析一座45 m高的土壩,其邊坡為1 V∶1.5 H和1 V∶3 H。這些斜率代表了現場觀察到的極端幾何結構。圖1 顯示了邊坡為1 V∶1.5 H的大壩的結構組成,大壩建在彈性基巖上,基巖上覆12 m厚的均勻沖積層。大壩由粘土心墻、砂殼組成,礫石護堤組成。

通常在快速下降期間觀察到上游殼的破壞,所以在整個研究過程中,選擇一個合適的點（圖1 中的“A”點）來研究水位下降引起的位移。本研究考慮了水庫地下水位對快速降深的影響,每次分析都選A點。

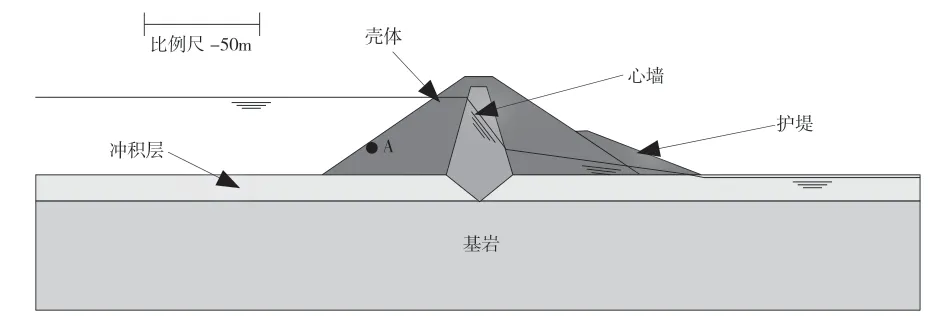
圖1 壩的結構組成

假定模型邊界條件在基巖底部完全約束,假設模型的上游和下游具有恒定的水頭邊界條件。上游壩坡上的初始水位與兩個假定水庫水位（25 m和35 m）相對應。下游水位被認為低于沖積層表面1.1 m。

不同區域的材料特性和本構關系如下,在建模時將基巖看作是具有剪切波速Vs=900 m/s（或剪切模量G=1800 MPa）的線彈性材料。將心墻看成滿足莫爾-庫侖,有效強度參數值為c'=0 kPa和φ'=36°,假設心墻的剪切模量值G=43 MPa。壩體所有區域的泊松比v均為0.35。使用HS小應變模型來定義壩殼、護堤和沖積層。對新模型進行標定,得到與PM4砂土有相似強度和剛度參數的小應變水平模型。等效模型校準的步驟如下。

PM4 砂模型的硬化土小應變（HSS）模型：壩殼、沖積層和礫石護堤的建模對應于干凈砂校正標準貫入試驗錘擊數,（N1）60cs=14 和相對密度,DR=55%。PM4 砂模型需要三個主要輸入參數DR、G0和hpo；其中,G0是剪切模量,hpo是校準因子。因此,針對與假定的（N1）60cs值相對應的這三個輸入參數對PM4 砂模型進行了校準。然而,目前的分析是使用HSS模型,而不是PM4 砂模型。HSS模型的主要輸入參數為、和m。其中,參考小主應力101 kPa時的小應變剪切模量,γ0.7是Gsecant=0.722G0時的臨界剪切應變。和分別代表三軸排水試驗中的割線剛度,固結儀試驗的切線剛度和三軸排水試驗的卸載/再加載剛度。

G0的值最初是根據假定的（N1）60cs值,使用以下公式得出：

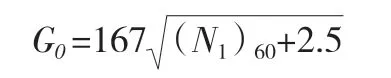
采用不排水直接剪切試驗進行數值模擬,確定hpo。在施加循環荷載之前,構件在σatm=101 kPa下固結,K0值等于0.5。hpo系統地變化,以模擬在遭受7.5 級地震（以15 個周期表示）時,在0.15 的循環應力比下（對應于（N1）60cs=14）經歷液化的土壤。假設土壤在15 個循環結束時累積3%的剪切應變時液化,并使用相對應的hpo值進行后續分析。

使用校準模型的直接剪切模擬提供15 個加載循環下的剪應力與剪應變,得出和分別為56.9 MPa和20.3 MPa,從而得到γ0.7的值為0.02%。考慮到材料在排水三軸試驗中的小應變彈性行為,值由獲得,其中,vur是卸載/再加載泊松比。小應變彈性模量（E0）對應的靜態彈性模量（Es）和動態彈性模量（Ed）之間的近似關系,小應變土壤剛度的E0≈Ed和Es≈Eur值。因此,得出E0值為36.5 MPa。,因此,的值約為18.3 MPa。此外,對于該模型,參考的值近似等于。

表1 大壩不同區域的模型類型和參數

圖2顯示了由軟件生成的有限元網格,分三個階段進行分析。首先,對壩堤進行初始靜態條件分析,然后檢查邊坡在快速下降現象中的響應,最后評估低水庫水位條件下壩堤的穩定性。

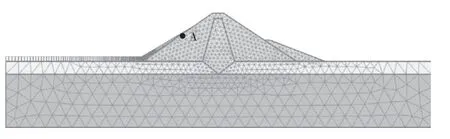
圖2 壩的有限元網格

對快速降深過程中粘土心墻各向異性的影響進行敏感性分析。結果表明,與心墻相比,殼層的各向異性對計算結果的影響更為深遠。因此,本文的研究范圍僅限于砂殼各向異性的研究。本研究假設了三種不同的水位下降率V,分別為0.1 m/d、0.5 m/d和1 m/d。最初分析兩個極限坡度下25 m和35 m地下水位。對于本研究,假設CPT耗散試驗結果提供了水平滲透系數kx的合理估計。因此,考慮殼體材料在垂直方向上的各向異性比ky=kx/1、ky=kx/2 和ky=kx/4,對不同情況進行分析。對于上述各向異性比,了解其他參數的影響,如坡度角、水位下降速度和水位下降前的水庫水位。

3 結果與討論

水庫水位的快速下降會引起邊界條件的突變,進而影響上游殼體的穩定性。圖3 顯示了1 V∶1.5 H坡比和各向同性滲透特性的大壩上游殼體的水位下降引起的破壞狀態。初始蓄水位為沖積層頂部以上35 m。假定地下水位迅速下降至沖積層上方5 m,導致上游殼體內部產生多余孔隙水壓力。這導致材料內的有效強度降低,并導致上游邊坡破壞。對于不同的分析方案,A 點產生的位移見圖3。

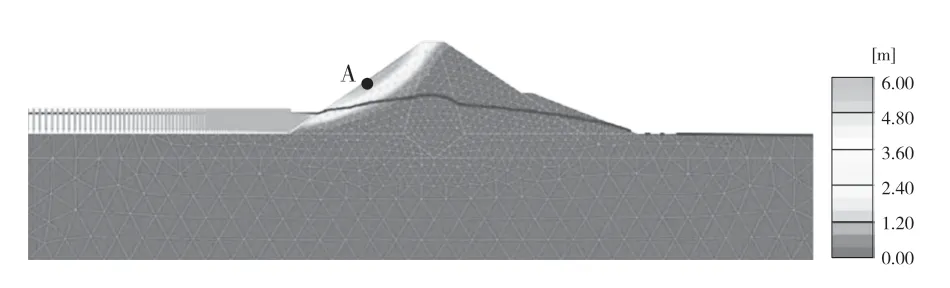
圖3 快速下降后出現的變形斜率和相應的位移

圖4 a和4 b顯示了兩個極端坡比在水位下降結束時A點位移的變化。各向異性滲透性的影響,就A點位移估計誤差而言,兩個大壩有相似的趨勢。隨著各向異性比從1 增加到4 , A點的位移逐漸增加（圖4）。當水位下降速度增加時,兩個斜坡趨勢相似。對于陡坡且水位下降速率為1 m/d的大壩,在各向同性情況下,最大位移為6.2 m。然而,對于各向異性情況,發現位移達14.2 m（圖4 a）。對于平坡,這些值分別為0.22 m和0.25 m（圖4 b）。

各向異性比增加會導致殼體在垂直方向上滲透率降低,與各向同性的滲透性相比,這導致殼體對多余孔隙水壓力耗散的阻力更大。多余孔隙水壓力消散的延遲會導致有效強度降低,并導致A點處更大位移的累積,見圖4。相反,在各向同性滲透性（即ky=kx/1）的情況下,超孔隙水壓力的消散速度相對較快,A點的位移最小。圖4 所示結果的對比表明,對于坡度較陡大壩,各向異性滲透性的影響更加明顯。這是因為較陡坡中存在較高初始靜態剪應力（與平坡相比）的影響,這種高初始靜態剪應力會對邊坡產生更大的失穩力,從而在快速下降過程中產生更大的累積變形。

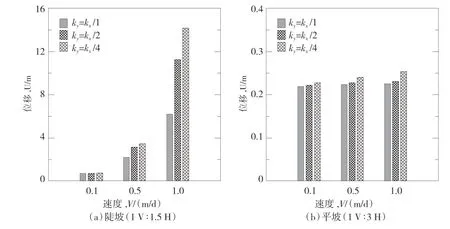
圖4 不同沉降速度和土的各向異性比率下A點的位移

圖5 a和5 b顯示了不同坡比的下降速度和各向異性的影響,位移估計誤差的比較。在陡坡（圖5 a）的情況下,當下降速度較低時,各向異性的影響可以忽略不計。然而,隨著速度的增加,如果在數值模擬中假設各向同性滲透率特性,則會低估臨界位移情況。緩慢的下降速度為砂殼中多余孔隙水壓力的消散提供了足夠的時間,這可防止有效應力（和抗剪強度）的降低,否則會導致上游邊坡不穩定。對于1 m/d的下降率,在陡坡上的估計誤差高達125%。然而,在平坡情況下（圖5 b）,觀察到材料的各向異性行為對邊坡穩定性的影響可以忽略不計,而與各向異性比無關。所以下降速度對陡坡的影響比平坡更為顯著。

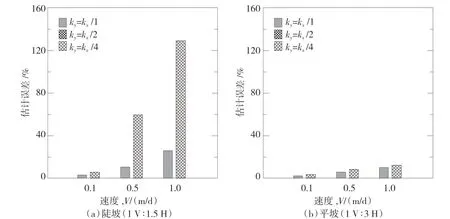
圖5 位移估計誤差百分比

為進一步研究各向異性比對大壩穩定性的影響,對不同庫水位的大壩進行參數研究。表2 列出了A點的位移值。從圖4 和圖5 可以看出A點的位移隨地下水位下降速度增大,及巖土各向異性的增大而增大。分析不同降深率和殼體材料各向異性對水庫地下水位的影響。在此研究中,下降速度為0.1 m/d和1.0 m/d,各向異性比1 和4 代表了現場可能出現的極值。

從表2 可以看出,當水庫水位較高且坡度較陡時,快速下降的影響最為顯著。隨著庫水位降低,邊坡變平,各向同性和各向異性滲透率的數值分析提供了水位下降期間上游殼體穩定性的相似信息。

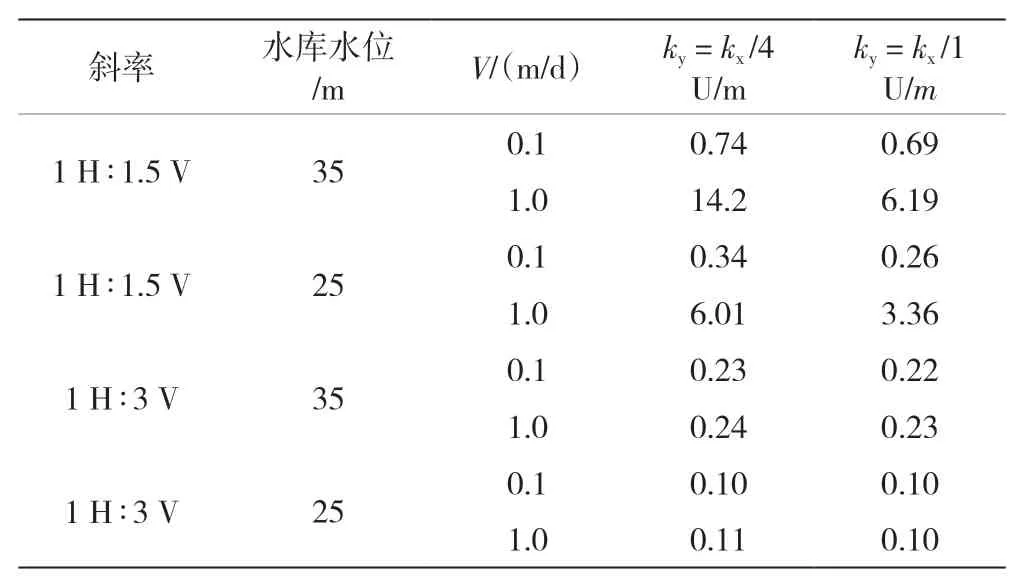
表2 地下水位對A點位移的影響

4 結論

在快速下降現象中,水庫水位的突然排放導致不平衡力的發展。現有的數值方法假設巖土材料是各向同性的。然而實際上,多孔材料在性質上是各向異性的。根據不同的各向異性比對垂直滲透系數進行了修正,并對邊坡的穩定性進行了分析。研究得出的結論如下：

1）在快速降深分析中,各向同性滲透率的假設會不可避免地導致對位移的錯誤估計。假設各向同性滲透率特性,通過數值分析預測的位移值預計將小于現場可能出現的位移值。

2）與平壩相比,各向異性對陡坡壩的穩定性影響較大。如果忽略壩殼的各向異性,則陡坡壩（1 V∶1.5 H）上游壩殼的位移估計值可能被低估（V=1 m/d,ky=kx/4的估計誤差約120%）。

3）各向異性的影響隨著水位下降速率的增加而顯著。

4）對于較高的水庫水位,與較低的水位相比,各向異性的影響更為顯著。