基于歐拉角的捷聯慣性組合導航濾波算法比較?
田佳玉 胡柏青 李開龍 趙仁杰
(海軍工程大學 武漢 430033)
1 引言
捷聯慣性導航系統(Strapdown Inertial Navigation System,SINS)基于在價格體積以及算法等方面的優勢,目前已成為研究的熱門領域。慣導系統中慣性測量元件的器件誤差積累等問題,會導致導航精度的下降,而組合導航正可以就這一問題進行改善。以捷聯慣導為核心,其他導航設備輔助的組合模式,被稱為捷聯慣性基組合導航,GPS(Global Positioning System,全球定位系統)[1]和 DVL(Doppler Velocity Log,多普勒計程儀)[2]常作為輔助導航設備。組合導航的基礎是現代濾波技術,根據慣導系統模型線性或非線性,可將濾波技術分為線性濾波和非線性濾波。線性濾波中最經典的當屬卡爾曼濾波(Kalman Filtering,KF)[3],在非線性濾波中,1995年S.J.Julier和J.K.Uhlmann提出的無跡卡爾曼濾波算法(Unscented Kalman Filter,UKF)估計精度較高且計算量一定[4~5]一直是研究的熱點。
除了考慮慣導模型,在捷聯慣性基組合導航濾波中,姿態表達方法也是需要重視的。采用不同的姿態表達方法所構造的組合導航濾波算法是不同的,常見的姿態表達方法有三維矢量的Euler角、羅德里格斯參數族以及四維矢量的四元數[6~8]。其中Euler角法僅需要求解三個微分方程,數量較少,但存在一對奇異點[9]在特定點姿角突變,無法得到準確值。在20世紀70年代末期,中國飛行試驗研究院黃雪樵[8]提出一種雙歐拉法,利用正反兩組歐拉方程結合使用可以解決奇異性問題。目前國內外學者對于組合導航濾波算法的研究取得了諸多成果,Hamiltn在進行附屬的虛數部研究中,提出了四元數概念[11],在四元數體系下,乘性拓展卡爾曼濾波是基于四元數與拓展卡爾曼濾波的結合[12~13],2003年,融合四元數與UKF,Markley、Crassidis提出采用“分層濾波”方式進行濾波估計[14]。
但目前對于Euler角體系下的線性濾波(Euler-KF)、非線性UKF濾波(Euler-UKF)、以及雙歐拉UKF濾波(DoEuler-UKF)三種組合濾波算法在實際捷聯慣性基組合導航系統中的精度、收斂速度和差異性還未進行研究分析。本文正是基于此,開展相關理論研究,通過仿真實驗展開探究三種組合導航濾波方法在應用中的優缺點,為組合導航濾波的選取與使用提供有益參考。
2 捷聯慣導基本模型
捷聯慣導基本方程包括姿態、速度和位置微分方程,分別為


3 雙歐拉角姿態解算法
歐拉角雖然使用簡單易懂且獨立方程數最少,但是一旦俯仰角達到±90°時方程組就會出現奇異點,進而無法確定橫滾角與航向角的大小。于是可以考慮采用正反兩組歐拉方程進行交替運算,避開各自奇異點。
動坐標系相對參考坐標系方位,由動坐標系依次繞3個不同軸轉動的3個轉角來確定,如果三個軸的順序是y-z-x,則令對應的航向角、俯仰角和橫滾角為正歐拉角,分別記為 φ、θ、γ,如圖1(a)所示,角速度為。如果變換順序是y-x-z,則航向角、橫滾角和俯仰角為反歐拉角,分別記為φr、γr、θr如圖1(b)所示。
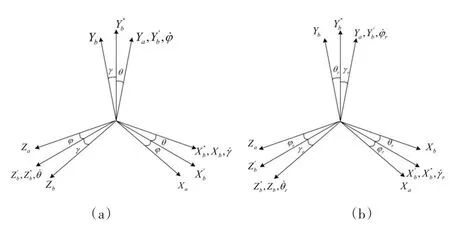
圖1 正、反歐拉坐標系旋轉
兩坐標矩陣的轉換可分解為三個單一旋轉矩陣的連乘,令導航坐標系為n,載體坐標系為b,則相應的正歐拉姿態矩陣可表示為
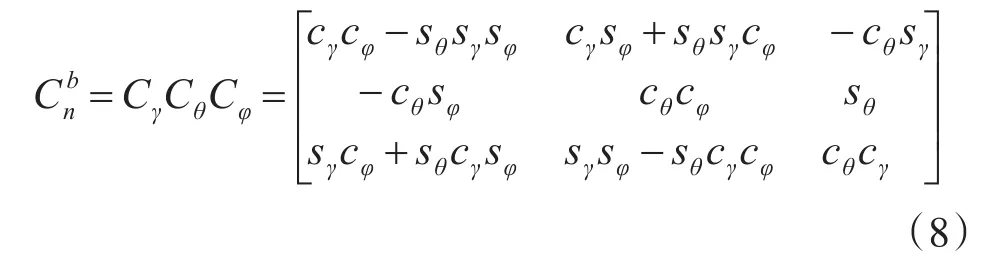
Cx表示關于x的單位旋轉矩陣。
角速度與歐拉角的關系可表示為
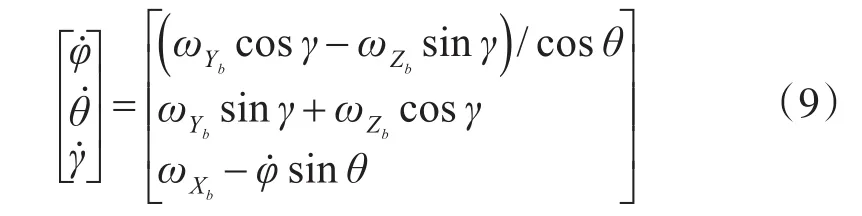
由上述可知:θ=±90°為方程組的奇異點,θ=0°或在π附近時,精度會提升,此范圍被稱為正歐拉方程的精華區。
可知,反歐拉方程的奇異點和精華區與正歐拉方程相反,奇異點在0°或π,精華區在±90°附近,正歐拉方程與反歐拉方程的精華區與奇異區呈現出的是一個倒掛關系。在應用的過程中,一般是以±45°或±135°為界劃分精華區和奇異區,如圖2。
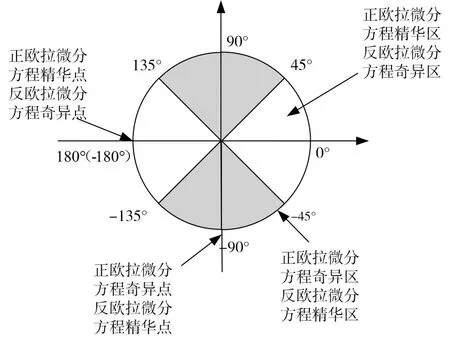
圖2 正、反歐拉角微分方程的精華區與奇異區
4 卡爾曼濾波
xk、zk分別為狀態向量和量測向量,Φk|k-1為狀態轉移矩陣,Γk為噪聲矩陣和Hk為量測矩陣,wk、vk分別為系統噪聲和量測噪聲且
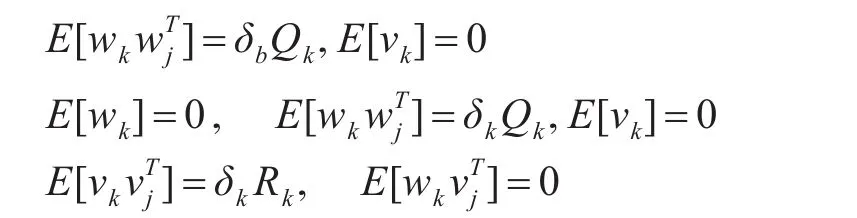
δkj為狄拉克函數,利用量測量獲得狀態最優估計值x?k的KF濾波過程由狀態一步預測、一步預測均方差、濾波增益、狀態最優估計、狀態估計均方差陣組成,見式(10)。
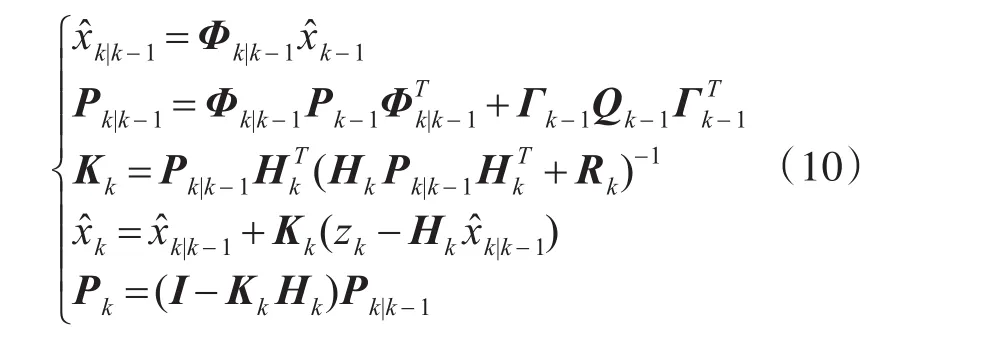
5 無跡卡爾曼濾波
UKF是以UT變換為基礎,選取相應的Sigma采樣點來近似系統狀態的先驗統計特性,再直接通過非線性方程演化系統狀態的后驗分布特性。當系統的過程噪聲和量測噪聲為加性噪聲且量測方程是線性的時候能夠得到簡化的UKF算法,簡化的UKF濾波算法如下:

6 基于雙歐拉角的無跡卡爾曼濾波
由于歐拉角存在奇異性,本文采用雙歐拉角法結合UKF進行濾波,基本的濾波流程如圖3所示。
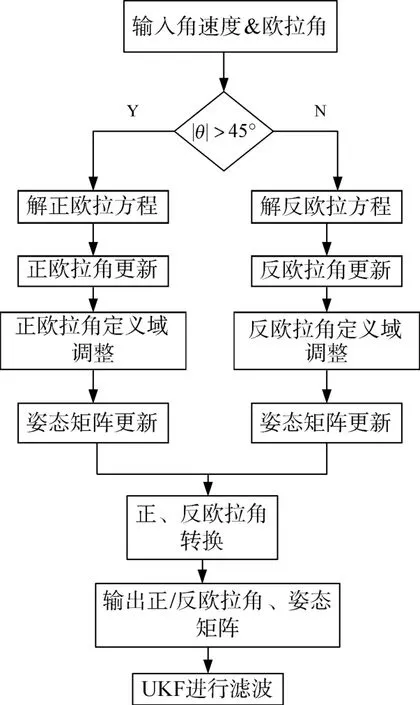
圖3 DoEuler-UKF濾波流程
7 實驗及分析
7.1 組合導航仿真實驗
通過仿真實驗對以上三種方法的估計效果進行比較,采用位置作為量測量SINS∕GPS松組合方式,仿真產生的航行軌跡如圖4所示,仿真時長1300s。
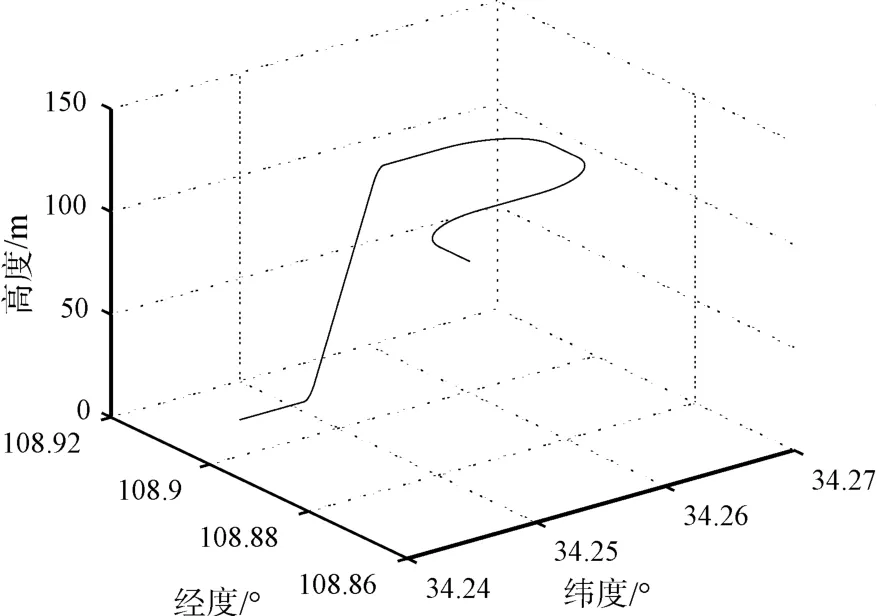
圖4 仿真航跡
設置濾波器的初始條件:

7.2 實驗結果分析
實驗的主要目的是比較Euler-KF、Euler-UKF和DoEuler-UKF的濾波效果,結果分別如圖5~6所示。
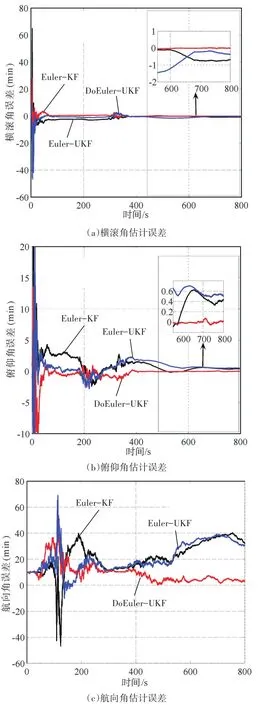
圖5 姿態角估計誤差比較
表1是位置和航向均方根誤差(RMSE)統計數據,RMSE方程由式(12)表示:
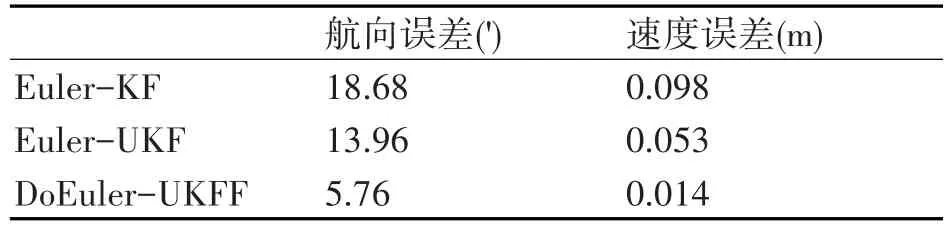
表1 位置、航向估計誤差均方根誤差
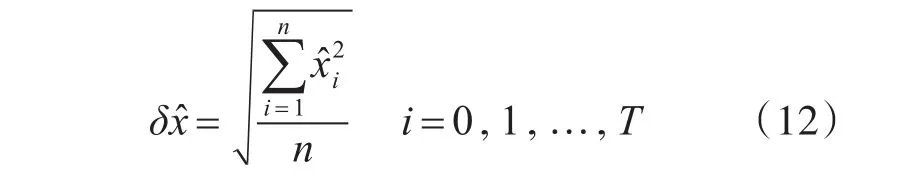
其中δx?是RMSE,T是實驗時長,計誤差值。
通過分析圖5的姿態估計效果,可以發現DoEuler-UKF的精度要明顯高于Euler-UKF和Euler-KF,Euler-UKF濾波效果好于Euler-KF。圖6是速度誤差估計,從收斂過程可以看出,DoEuler-UKF的收斂速度明顯比Euler-UKF和Euler-KF要快。通過表1可以看出,在誤差精度方面,DoEuler-UKF要明顯好于其他兩種方法,這是由于Euler-KF方法采用的是線性誤差模型,忽略了非線性部分,導致了精度下滑,而Euler-UKF采用的則是非線性誤差模型,各項參數考慮更為全面,然而Euler的姿態表示方法存在一定局限性,一旦達到奇異點附近,精度便會受到較大影響,DoEuler-UKF既選用了更為準確的非線性模型,又克服了歐拉角的奇異性問題,因此達到了更為理想的濾波估計效果。
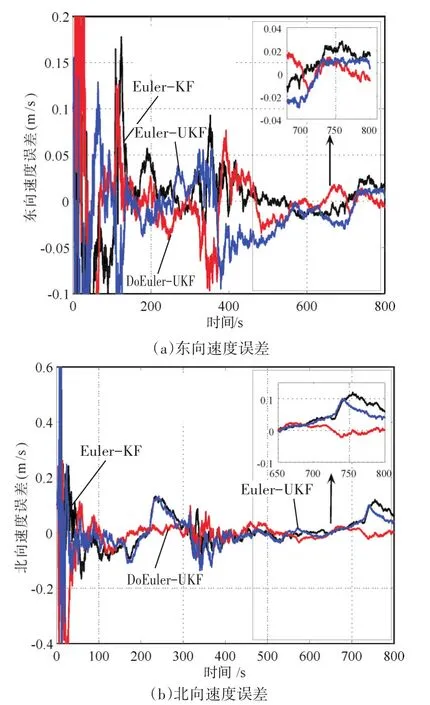
圖6 速度估計誤差
8 結語
Euler角法作為旋轉物理意義最明顯的姿態表示方法,奇異點的存在限制了它的精度與應用范圍,而雙歐拉法,利用正反歐拉方程的變換,巧妙避開奇異區,并對解的精華區劃分,有效提高了姿態的精確性。結合不同的慣導模型,對Euler-KF,Euler-UKF與DoEuler-UKF濾波比較實驗進行分析:DoEuler-UKF對比Euler-KF和Euler-UKF,航向估計精度分別提高了69.5%與58.7%,速度估計精度分別提高了85.7%與73.6%。

