基于解析法的電-熱互聯綜合能源系統概率潮流計算

李紅，王文學，伏祥運，何維祥，王煒，袁斌，王舒捷

(國網江蘇省電力有限公司連云港供電分公司，江蘇 連云港 222000)

0 引言

區域綜合能源系統以電力系統為核心，綜合考慮電、氣、熱等多種用能需求，形成具有多能協同特征的綜合系統[1—4]。但目前電力系統、熱力系統等普遍存在獨立規劃、獨立運行的特點，各種能源網絡間缺乏有效交互，難以發揮多能源系統的耦合互補的優勢[5—7]。電-熱系統穩態潮流屬于確定性分析，是對綜合能源系統深入研究的基礎。綜合能源系統穩態潮流主要從模型和求解方法兩方面進行研究：在模型方面，電網穩態潮流方程是由節點功率方程組成的非線性方程組[8]。氣網穩態模型包括管道流量方程、加壓站方程和節點流量平衡方程[9]。熱網穩態模型主要包括水力模型和熱力模型[10]。目前主要利用牛拉法求解非線性方程組，一般分為統一求解和順序求解[11]。

隨著新能源的大量并網，負荷的不確定性增大，同時能源轉化設備應用日益廣泛，增強了不同能源系統間的耦合程度，因此綜合能源系統包含大量不確定性因素[12]，如各類負荷或新能源出力的波動、故障等，且不同能源網絡之間存在相互影響，某網絡的波動可能造成綜合能源系統潮流分布產生根本性的變化[13]。僅通過確定性分析難以把握綜合能源系統在不確定環境下的運行狀態，概率潮流能夠充分考慮這些不確定性因素，從而更全面地反映系統運行狀況。

目前，概率潮流的求解方法一般包括模擬法、解析法和近似法。模擬法中常用蒙特卡洛法，通過生成大量場景，尋找狀態量的概率信息[14]，文獻[15]提出一種電-熱互聯系統概率潮流計算方法，定量評估電轉熱技術對系統概率潮流影響。解析法中常用的是半不變量法[16—17]，文獻[18]提出一種基于多點線性半不變量法的電-熱互聯系統概率潮流計算方法，定量得到相關狀態量的概率信息。近似法中常用點估計法，優點為無需求解輸入輸出的具體關系，但相比其他2種方法，計算精度一般較低[19]。文獻[20]提出一種計及相關性的電-氣-熱綜合能源系統概率最優能量流計算方法，并采用基于Nataf變換的三點估計法對該模型進行求解。

熱網方程具有強非線性，以往半不變量法將狀態量描述為關于電-熱負荷的線性方程，一般無法同時滿足計算復雜度、精度和計算速度的要求。文中基于解析法和近似法，提出一種輻射狀供熱網絡概率潮流快速計算方法，將狀態量描述為關于電-熱負荷的非線性方程，可直接獲得管道流量和節點溫度的概率信息，顯著提高了計算速度和求解精度。

1 熱網模型

1.1 熱網非線性模型

熱網模型包括水力模型和熱力模型[21]，水力模型包括流量平衡方程和管道壓降方程：

Am=mq

(1)

hf=Km|m|

(2)

式中：A為系數矩陣；m，mq分別為管道流量向量和熱負荷流量向量，kg/s；hf為環路管道壓降組成的向量，m；K為環路管道阻尼系數組成的向量；|m|為管道流量的絕對值。

熱力模型包括熱負荷方程、管道溫降方程和熱功率守恒方程。

Φ=Cpmq(Ts-To)

(3)

Tend=(Tstart-Ta)e-λL/(Cpm)+Ta

(4)

Tout∑mout=∑(minTin)

(5)

式中：Φ為熱負荷向量，MW；Cp為水比熱容，且Cp=4 182 J/(kg·℃)；Ts，To分別為節點供水溫度向量和回水溫度向量，℃；Tstart，Tend，Ta分別為管道首端溫度、管道末端溫度和環境溫度，℃；λ為傳熱系數，W/(m·K)；L為管道長度，m；min，mout分別為注入節點流量向量和流出節點流量向量，kg/s；Tin，Tout分別為流入節點溫度和節點混合溫度，℃。

熱網方程式(1)—式(5)中含有指數方程，非線性程度較高，且管道流量與節點溫度為乘積關系，耦合程度較高。目前常采用牛頓法求解穩態潮流，計算較為復雜，甚至可能存在不收斂等問題。

1.2 電熱耦合元件模型

熱電聯產機組分為定熱電比機組和變熱電比機組2種，分別用式(6)和式(7)表示。

Cm=ΦCHP/PCHP

(6)

Cz=ΦCHP/(ηeFin-PCHP)

(7)

式中：Cm，Cz分別為機組的定熱電比和變熱電比；ΦCHP，PCHP分別為機組的熱出力和電出力；ηe，Fin分別為機組的冷凝效率和燃料輸入速率。

1.3 輻射狀熱網概率潮流模型

兩節點供熱網絡如圖1所示，圖中TH，TH1，TH2分別為熱源溫度、節點1溫度和節點2溫度；mH為熱負荷流量。利用管道溫降方程式(4)與熱負荷功率方程式(3)推導[22]可得式(8)。

圖1 兩節點供熱網絡Fig.1 District heating network with two nodes

(8)

式中：TR為熱負荷回水溫度；Φ2為節點2的熱負荷。將式(8)推廣至多根管道，如式(9)所示。

(9)

多節點供熱網絡如圖2所示，對于含有分支的節點，此時m1≠m2≠…≠mi，其中m1，m2，…，mi-1為管道流量，mi為熱負荷流量。

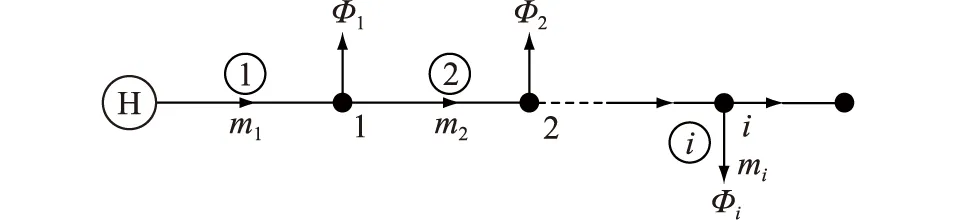
圖2 多節點供熱網絡Fig.2 District heating network with multiple nodes

圖2中，引入變量n1，n2，…，ni，令n1=m1/mi，n2=m2/mi，…，ni-1=mi-1/mi，ni=mi/mi=1，代入式(10)可得mi為：

(10)

由于潮流計算前管道流量未知，令：

(11)

式中：k為熱負荷流量mi經過的干路管道編號；Φi為節點i的熱負荷；Qk為管道k所流入熱能的期望值，因此n1，n2,…,nk將為定值[22]。

因此，由隨機變量的數字特征，mi的均值和方差可表示為：

(12)

(13)

式中：E(mi)為管道i中熱負荷流量mi的均值；D(mi)為管道i中熱負荷流量mi的方差。由于比熱容Cp=4 182 J/(kg·℃)，則當式(12)中ni為定值時誤差較小，因此由熱負荷的均值和方差可得管道流量的均值和方差。將熱負荷功率方程式(3)代入式(10)，移項變形可得式(14)。

(14)

再由隨機變量的數字特征可得：

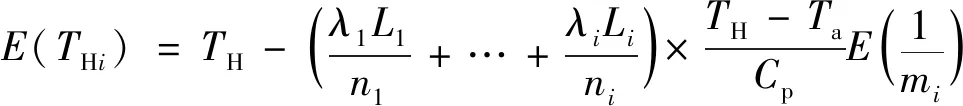
(15)

(16)

由式(15)、式(16)可知，得到流量倒數的均值和流量倒數的方差后，可獲得節點溫度THi的均值與方差。設正態分布隨機變量x=mi的均值和標準差分別為μi，σi，其概率密度函數為：

(17)

由連續型隨機變量的概率密度函數性質可知，y=1/x=1/mi，概率密度函數為：

(18)

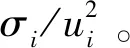
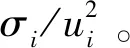
綜上所述，由式(12)和式(13)可得供熱網絡管道流量的均值與方差，由式(15)—式(18)可得節點溫度的均值與方差。求得熱電聯產(combined heating and power，CHP)熱出力概率分布后，由機組熱出力與電出力關系可得機組電出力概率分布，進而求得電網中各狀態變量的概率分布。

2 輻射狀熱網概率潮流算例測試

23節點輻射狀熱網算例如圖3所示，CHP源溫度恒定為80 ℃，負荷節點回水溫度恒定為45 ℃，環境溫度Ta為10 ℃，測試采用Matlab編程，仿真環境為1.9 GHz CPU，4.0 GB RAM的PC機。

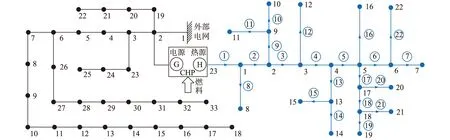
圖3 電-熱互聯綜合能源系統Fig.3 The diagram of combing electricity and heat networks

2.1 典型狀態量的均值與方差

若每根管道長度設置為500 m，所有負荷節點熱負荷均設置為0.5 MW，熱負荷波動均在±10%以內。文中方法和蒙特卡洛法所得流量均值、流量標準差分別為μm，σm，μm,mcs，σm,mcs；流量均值誤差百分數、流量標準差誤差分別為δμ,m，δσ,m。因此有:

δμ,m=(|μm-μm,mcs|/μm,mcs)×100%

(19)

δσ,m=|σm-σm,mcs|

(20)

溫度均值、溫度標準差分別為μT，σT，μT,mcs，σT,mcs；溫度均值誤差百分數、溫度標準差誤差分別為δμ,T，δσ,T。因此有：

δμ,T=(|μT-μT,mcs|/μT,mcs)×100%

(21)

δσ,T=|σT-σT,mcs|

(22)

其中蒙特卡洛結果是采用熱網非線性模型計算所得，采樣20 000次。此時計算出的流量和溫度的均值與標準差如表1和表2所示，文中方法耗時0.019 6 s，蒙特卡洛法耗時1 720.105 4 s。

表1 所有管道流量均值和標準差的比較Table 1 Comparison of mean and standard deviation of all pipe flow

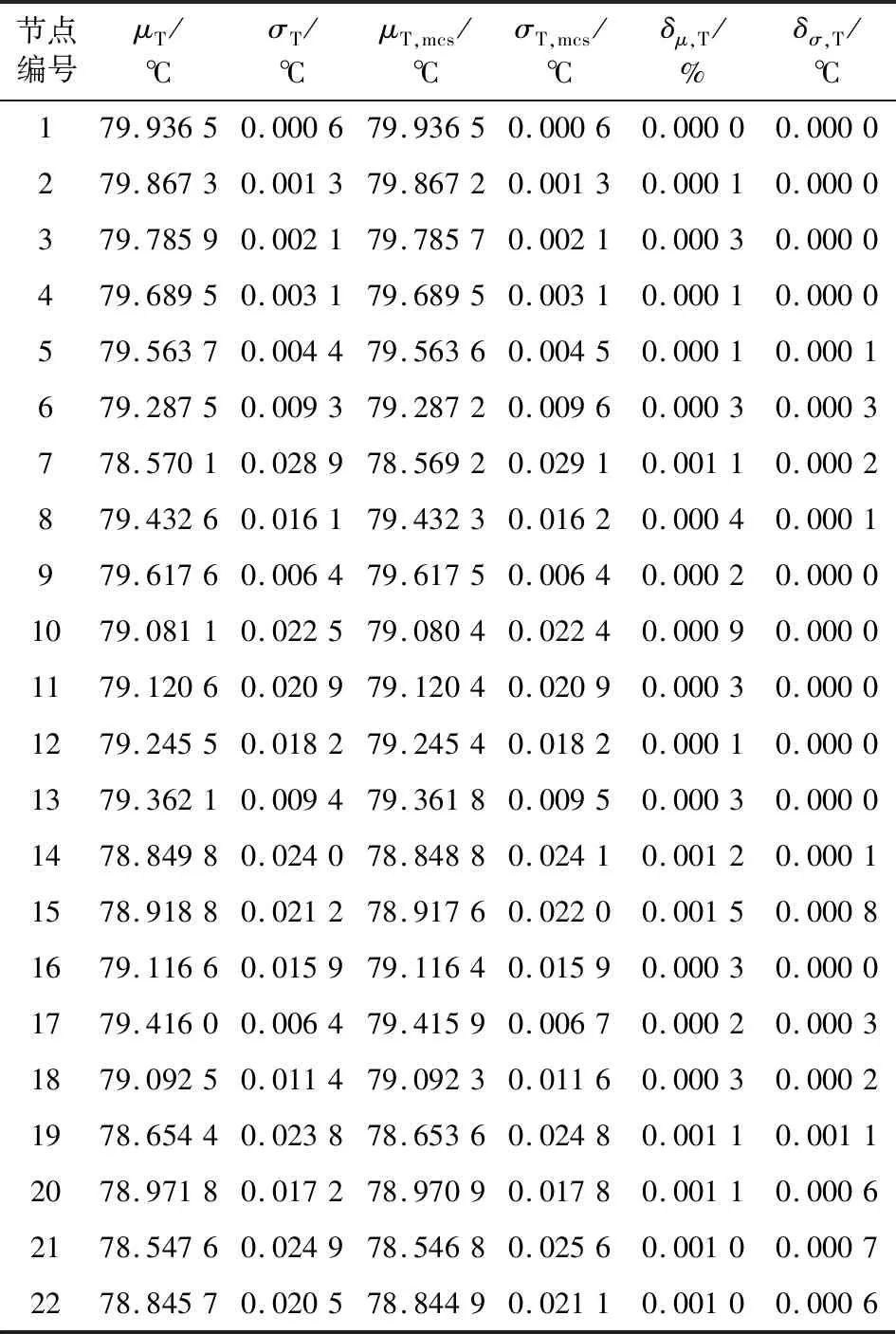
表2 所有節點溫度均值和標準差的比較Table 2 Comparison of mean and standard deviation of all node temperatures

由表1可知，管道流量均值誤差百分數最大值為0.024 4%，平均值為0.008 0%，管道流量標準差誤差最大值為0.003 1 kg/s，平均值為0.001 3 kg/s。由表2可知節點溫度均值誤差百分數最大值為0.001 5%，平均值為0.000 5%，節點溫度標準差誤差最大值為0.001 1 ℃，平均值為0.000 2 ℃。可見文中方法具有較高的計算精度和計算速度。

由表1可知，文中方法和蒙特卡洛法所得管道1的流量均值分別為42.266 9 kg/s和42.264 5 kg/s，2種方法求得的熱源節點回水溫度均值均為44.712 2 ℃，由式(3)計算可得熱源的熱出力相差354.176 9 W，若式(6)中定熱電比取1.3，則2種方法求得的熱出力誤差引起的電壓和相角誤差分別如圖4和圖5所示。

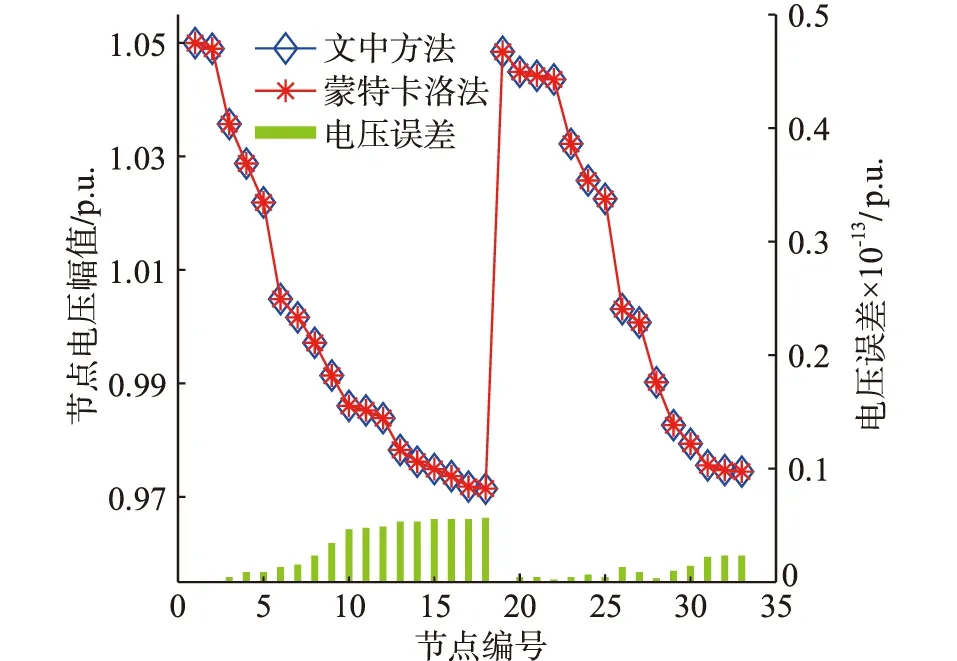
圖4 熱出力誤差引起的電網電壓誤差Fig.4 Error of voltage amplitude caused by thermal output

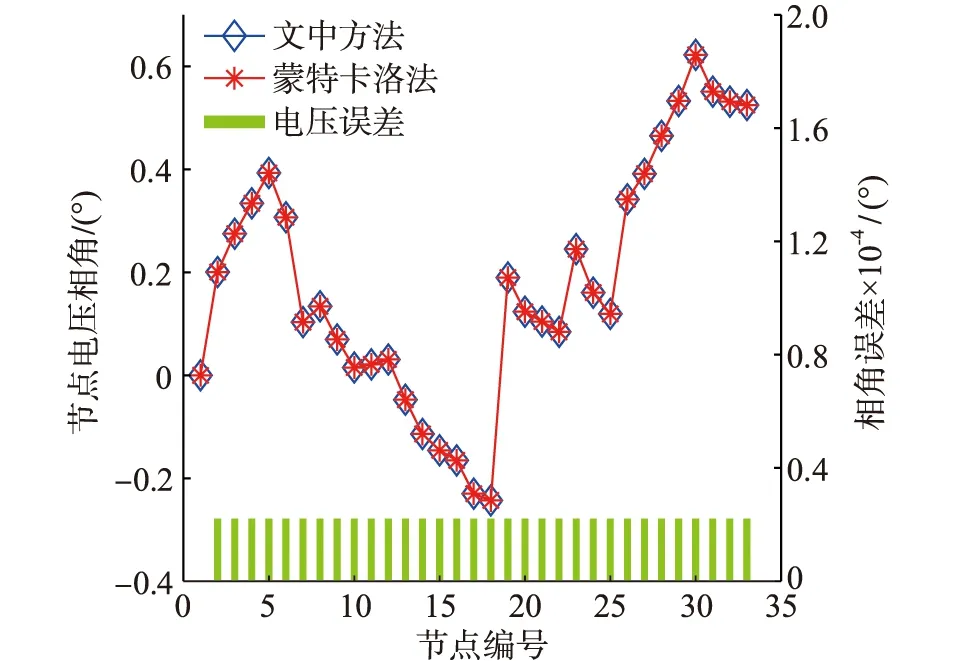
圖5 熱出力誤差引起的電網相角誤差Fig.5 Error of voltage phase angle caused by thermal output

由圖4和圖5可知，文中方法和蒙特卡洛法引起的電網電壓誤差和相角誤差極小，表明文中方法產生的誤差對電網影響極小，驗證了該方法的有效性與合理性。

2.2 控制變量法

(1)設置每個負荷節點熱負荷均為1 MW，所有熱負荷波動量為±10%且保持不變，逐漸同時增大每根管道長度，節點19溫度標準差見圖6(節點19溫度標準差誤差最大)。

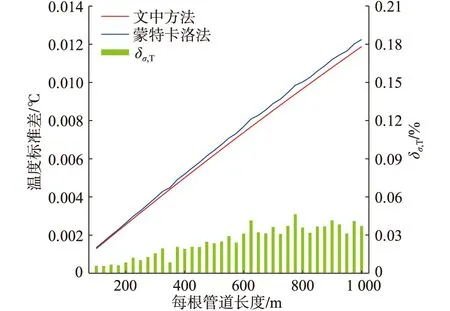
圖6 節點19溫度標準差隨管道長度變化情況Fig.6 The temperature standard deviation of node 19 varying with the length of the pipeline

由圖6可知，節點19溫度標準差與管道長度近似呈線性正相關，且δσ，T小于0.05%。

(2)設置每根管道長度為500 m，熱負荷波動量為±10%且保持不變，逐漸同時增大每個負荷節點熱負荷值，節點19溫度標準差如圖7所示。

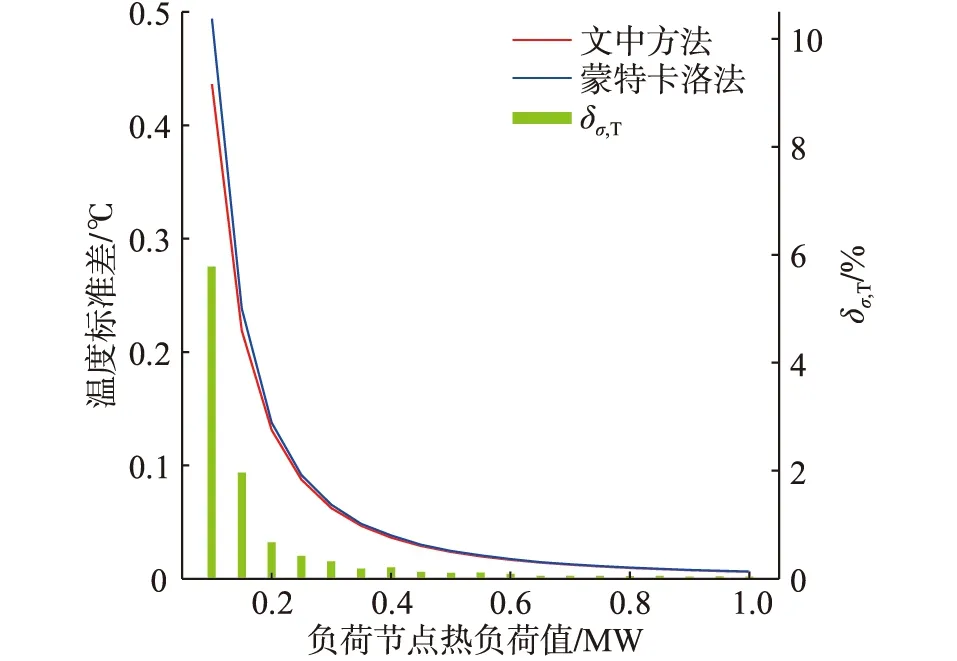
圖7 節點19溫度標準差隨熱負荷值變化情況Fig.7 The temperature standard deviation of node 19 varying with the heat load value

由圖7可知，節點19溫度標準差與熱負荷值呈負相關，且曲線的切線逐漸平緩，熱負荷值對節點溫度標準差的影響相對較大。同時，隨著熱負荷值的增大，文中方法的誤差逐漸縮小，當熱負荷值為1 MW時，節點19溫度標準差誤差小于0.02%。

(3)設置管道長度為500 m，熱負荷為1 MW且保持不變，逐漸同時增大熱負荷波動量，節點19溫度標準差如圖8所示。

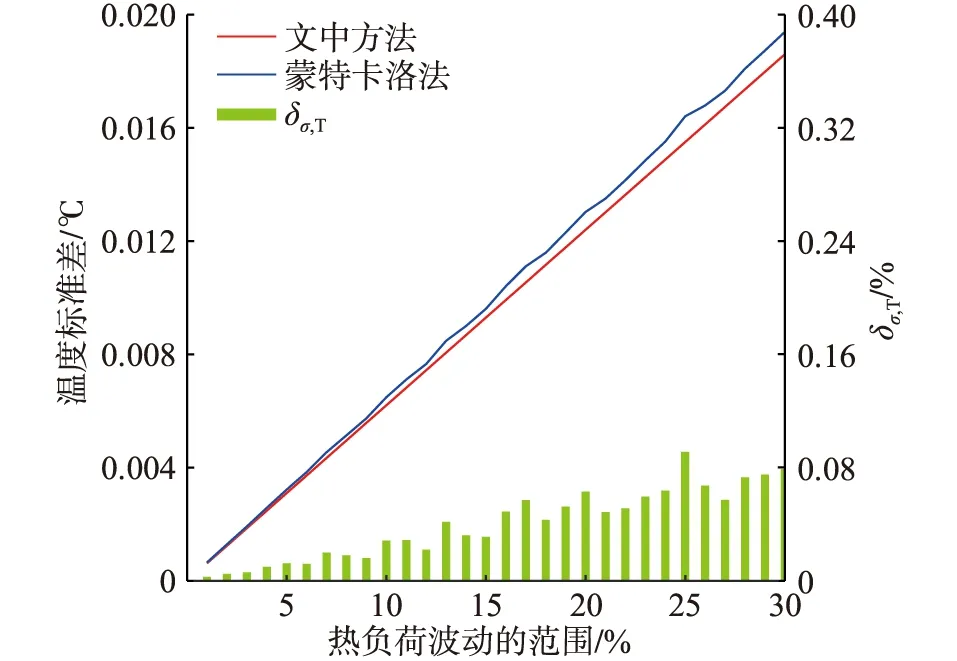
圖8 節點19溫度標準差隨熱負荷波動量變化情況Fig.8 The temperature standard deviation of node 19 varying with the fluctuation of heat load

由圖8可知，節點19溫度標準差與熱負荷波動量近似呈線性正相關，且δσ，T小于0.1%。

2.3 典型狀態量的三維關系圖

設置熱負荷波動量為±10%，當改變管道長度和熱負荷值時，采用蒙特卡洛法所得管道1流量標準差和節點19溫度標準差分別見圖9和圖10。

圖9 管道1流量標準差與管道長度和熱負荷的關系Fig.9 The relationship among the flow stand-ard deviation of pipe 1,the pipe length and heat load value

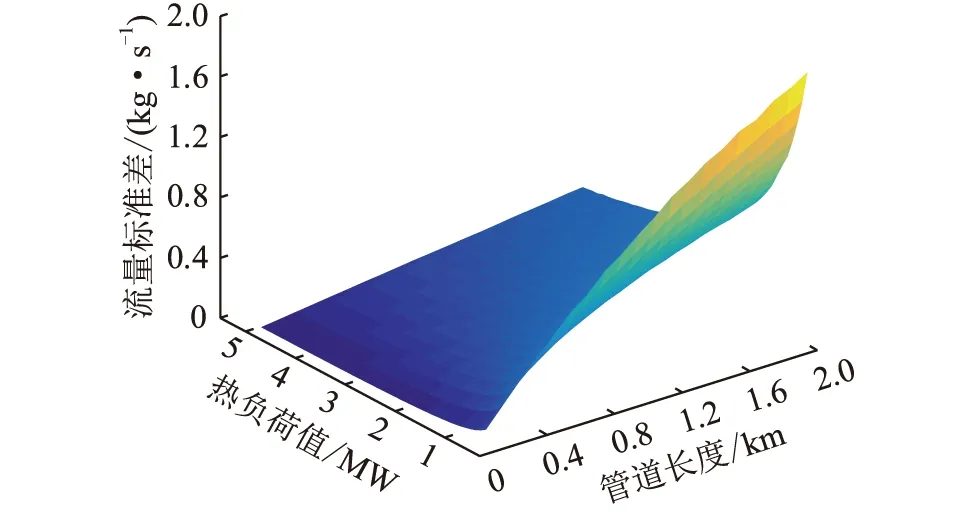
圖10 節點19溫度標準差與管道長度和熱負荷關系Fig.10 The relationship among the temperature standard deviation of node 19,the pipe length and heat load value

由圖9可知，管道長度與流量標準差沒有呈現相關性，熱負荷值與流量標準差近似呈線性正相關。由圖10可知，管道長度與節點溫度標準差呈正相關，而熱負荷值與節點溫度標準差呈負相關。

3 結論

文中提出了一種輻射狀供熱網絡概率潮流快速計算方法，可同時獲得熱力網的穩態潮流與概率潮流，無需迭代，計算準確度高且不存在收斂性問題，結論如下：

(1)管道長度與流量標準差沒有呈現相關性，管道流量標準差與熱負荷值近似呈線性正相關。

(2)節點溫度標準差與熱負荷波動量近似呈線性正相關，節點溫度標準差與管道長度近似呈線性正相關，節點溫度標準差與熱負荷值呈負相關。

(3)文中方法引起的熱源熱出力誤差對電網電壓和相角的影響極小。

文中方法在保證計算精度的同時，極大地提高了計算速度，可為綜合能源系統不確定性分析提供參考。下一步將研究大規模可再生能源并網對電-熱互聯綜合能源系統概率潮流的影響。

本文得到國網江蘇省電力有限公司連云港供電分公司伏祥運勞模創新工作室2021年研究項目“電-熱互聯綜合能源系統快速潮流計算方法與優化調度方法技術的研究與應用”(B110D02188D7)資助，謹此致謝！