基于比例風險模型的船舶狀態機會維修策略

李冀暉，黃錦敬，韋發清

（湛江科技學院，廣東 湛江 524094）

目前，船舶維修主要以事后維修和定期維修為主。針對一些易于監測的關鍵部件輔以狀態維修的檢修模式，這容易造成維修過度或維修不足等問題，對船舶運行的安全性和經濟性造成不利影響。針對船舶維修，國內外學者進行大量研究，魯金明等[1]建立以任務可用度及系統可靠度為約束，最低維修費用為優化目標的船舶最佳維修周期模型；張剛等[2]研究基于PMS 模型的船舶設備維修保養策略，綜合考慮維修時間、費用和可靠性的關系；江曉俐[3]針對船體結構維修問題，提出使用半Markov過程優化維修方案，使船舶單位時間營運成本降至最低；Si 等[4]采用連續Markov 鏈描述工作狀態對部件退化的影響，研究部件剩余壽命分布，提出計算剩余壽命的蒙特卡洛仿真算法；楊立乾等[5]構建船舶關鍵部件的Gamma 退化過程模型，制定船舶關鍵部件的狀態維修策略，該策略能顯著降低船舶關鍵部件的維修費用；杜黨波等[6]針對復雜設備的線性和非線性疊加的退化問題，提出一種基于維納過程的帶隨機參數和確定參數的混合退化模型，并采用Kalman 濾波技術和極大似然估計方法對模型中的隨機參數和確定參數進行求解；孫林凱等[7]研究維修次數對維修周期的影響，建立周期可變的船舶設備預防性維修模型，并用MATLAB 分析維修周期的的變化規律。這些學者從不同角度對船舶關鍵部件的狀態變化和壽命規律進行建模，并得到相應的維修決策方案，但從部件的綜合狀態進行定性和定量分析入手，研究其壽命規律比較少見。

比例風險模型（proportional hazard model，PHM）能將部件的狀態信息融合到壽命模型中，從而能更準確評估部件的壽命規律[8]。周志才等[9]針對船舶柴油機維修問題，采用威布爾比例風險模型描述系統狀態信息和失效率的關系，構建了視情維修決策模型；文獻[10-15]分別在不同領域構建基于設備狀態信息的比例風險模型，得到各自設備的維修策略。這些學者研究比例風險模型在不同設備領域的應用，但對船舶部件的維修，尤其是船舶關鍵部件的狀態機會維修則很少見諸報道。

本研究將比例風險模型應用到船舶維修上，首先根據船舶部件的運行時間、檢修歷史、家族質量史、運行環境、工作載荷和狀態信息等，利用層次分析法得到各因素的權重，進而計算出船舶部件的狀態指數，再結合部件的壽命數據估計出模型參數；同時引入機會維修思想，以減少部件拆裝等停工費用，以船舶關鍵部件的可靠度閥值為約束，建立船舶關鍵部件的狀態機會維修決策模型，以期為船舶關鍵部件的預防性檢修優化提供決策參考。

1 比例風險模型的建立及其協變量的確定

1.1 比例風險模型

比例風險模型能準確表達部件壽命與狀態參數、工作載荷、外部環境、家族質量和維修歷史等因素之間的關系，各因素在模型中以乘積的形式表示，稱為協變量[16]。比例風險模型的基本形式為

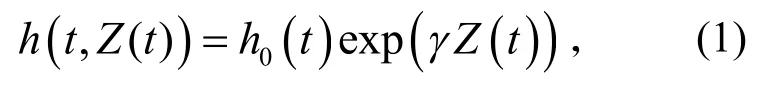
式(1)中h0(t)為基本風險率函數，只與時間有關；exp[γZ(t)]為協變量函數，Z(t)為t時刻的協變量，表示該時刻的設備狀態，γ是協變量的系數。由于威布爾分布廣泛適用于描述各種機械設備和部件的壽命分布，故采用威布爾分布作為基本風險函數，其表達式為

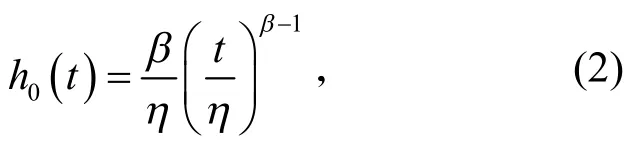
式(2)中β和η分別為威布爾分布的形狀參數和尺度參數。將其代入式(1)，可得到威布爾比例風險模型

從式(3)可看出，風險率除了與威布爾分布有關外，還與協變量Z(t)有關，即與協變量函數exp（γZ(t)）成比例關系。在同一時刻，協變量不同，風險率也不同。新部件和多次維修過的部件同時投入運行一段時間后，由于不完全維修會造成部件故障率遞增和役齡遞減[17]，故多次維修過的部件風險率更高。在惡劣環境中運行比在平順環境中運行風險率更高，超負荷運轉比在額定載荷以內運轉風險率更高等。所有這些因素都屬于風險模型的協變量，因此如何計算確定協變量成了關鍵。

1.2 協變量的確定

協變量實際上屬于設備或部件的整體運行狀態信息，這類信息有很多，需要合理、準確評估才能進行有效決策。目前，研究基于設備狀態的風險率時，主流方法有兩種：一是基于設備健康指數的反演方法[18]，二是基于設備缺陷指數和壽命數據擬合出風險率函數[19-20]。兩種方法分別從不同方向對設備風險率做出描述，不管是哪種方法都需要對設備的結構原理、歷史事件和運行狀態等進行準確和深入了解。根據船舶設備管理員的經驗和工程師的意見，綜合考慮各方面因素，確定船舶設備協變量分別由內外部環境、檢修記錄、家族質量史、缺陷記錄和狀態數據組成，記為Zi(t)(I=1,2,…,5)。即船舶設備協變量表示為式(4)中，γi為對應協變量分量的權重。為對各協變量分量的權重進行合理分配，采用具有主客觀分析方法優點的層次分析法進行權重計算[17]。

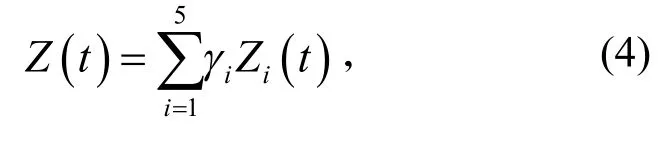
為便于評估，將船舶設備協變量的取值映射到0～ 1 之間，取值越接近0 表示設備狀態越健康，取值越接近1 表示設備狀態越差，協變量取值及其對應設備狀態的關系（表1）。

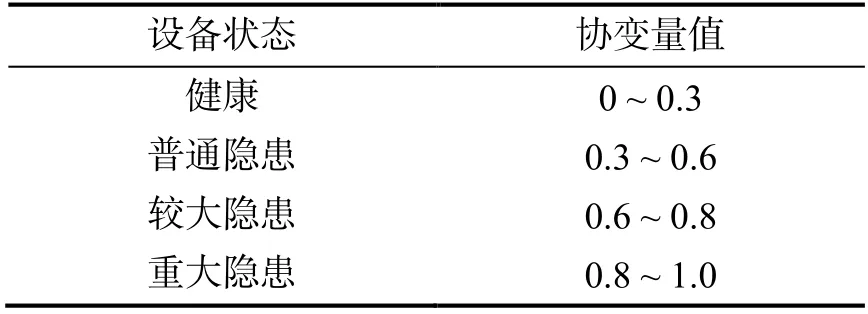
表1 設備狀態與協變量的對應關系Table 1 Correspondence between device state and covariate

各定性指標根據船舶的運行狀況、維修情況、自身質量，同時參照《船舶修理標準及技術要求》結合專家打分法確定，表2—5 分別為各定性指標的取值標準。

表2 內外部環境取值標準Table 2 Value standard internal and external environment

狀態數據為實時反映設備運行的狀態信息，如部件振動值、噪聲、油液狀況、溫度和壓力等，屬于定量指標，需要根據下式計算轉化為指標值。

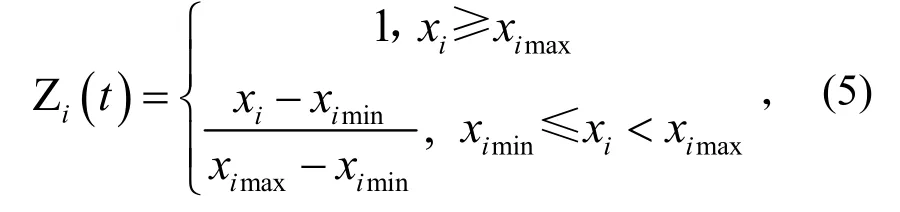
式(5)中，ximax表示該指標允許取值的上界，ximin表示該指標的最小值，xi表示該指標的當前值。

表3 檢修記錄取值標準Table 3 Value standard of maintenance record

表4 缺陷記錄取值標準Table 4 Value standard of defect record

表5 家族質量史取值標準Table 5 Value standard of family quality history

1.3 模型參數估計

威布爾比例風險模型（式(3)）還需估計3 個未知參數β、η和γ才能最終確定。由于船舶部件在使用中有相當部分是在尚未發生故障就被換下，壽命數據中存在截尾數據，而極大似然估計在處理不完全數據樣本時具有明顯的優勢，故采用極大似然估計法求模型參數。似然函數的一般形式[21]為

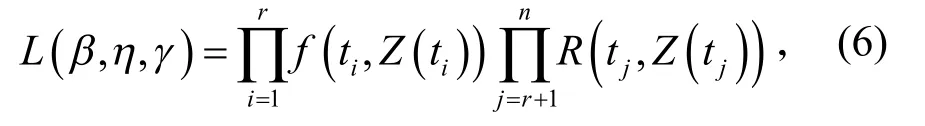
式(6)中，r為失效數據個數，n為壽命數據的總數，n－r為截尾數據個數，ti為部件i的失效時刻，tj為部件j的截尾時刻，Z(ti)為部件i在ti時刻的協變量，Z(tj)為部件j在tj時刻的協變量，f（t i,Z（ti））為部件i在ti時刻的概率密度函數，R（t j,Z（tj））為部件j在tj時刻的可靠度。由可靠性知識，得

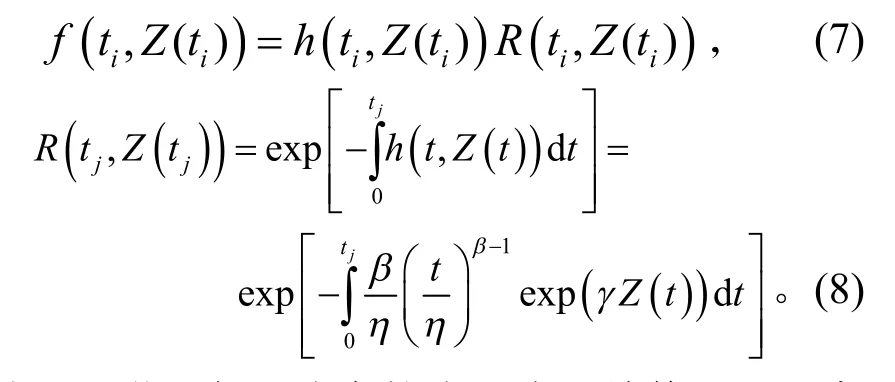
由1.2 節可知，在各協變量中，檢修記錄和家族質量史在部件的維修周期開始時即已確定，故每個檢測間隔期內不變，而缺陷記錄、內外部環境和狀態數據有可能發生變化，故協變量Z(t)不是連續值，而是離散值。在每個檢測周期內，協變量主要有5 種變化趨勢（圖1）：1）各協變量基本無變動，為一恒定值；2）內外部環境逐漸惡化或狀態值緩慢增加，協變量逐漸增大；3）內外部環境逐漸好轉或狀態值緩慢減小，協變量逐漸減小；4）在某個時刻部件突然發生缺陷或內外部環境突然惡化，協變量階躍升高；5）在某個時刻內外部環境突然好轉，協變量階躍降低。

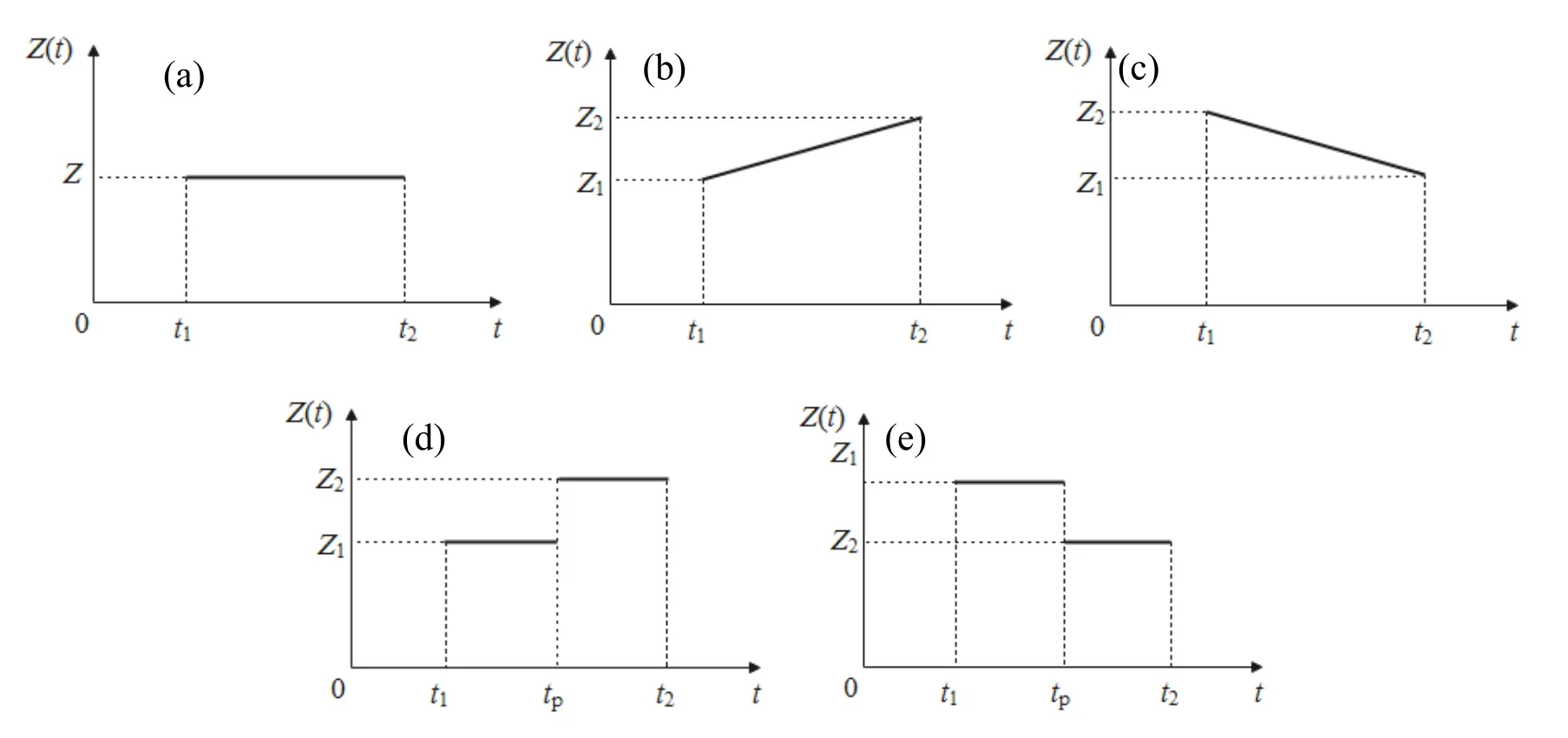
圖1 協變量的5 種變化趨勢Fig.1 Five trends of covariate change

由協變量的5 種變化趨勢可知，由于階躍和漸變性的存在，每個檢測間隔期內的協變量，如果取兩個檢測點中任一個檢測值都會造成較大誤差，而取兩個檢測點的平均值則可較好地消除誤差，即第r個檢測間隔期內協變量為

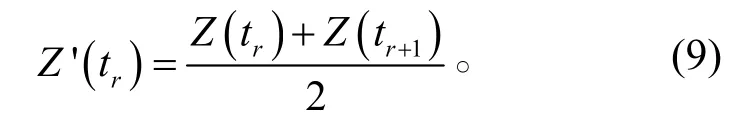
聯合式(8)和(9)，可得到可靠度的累積表達式為

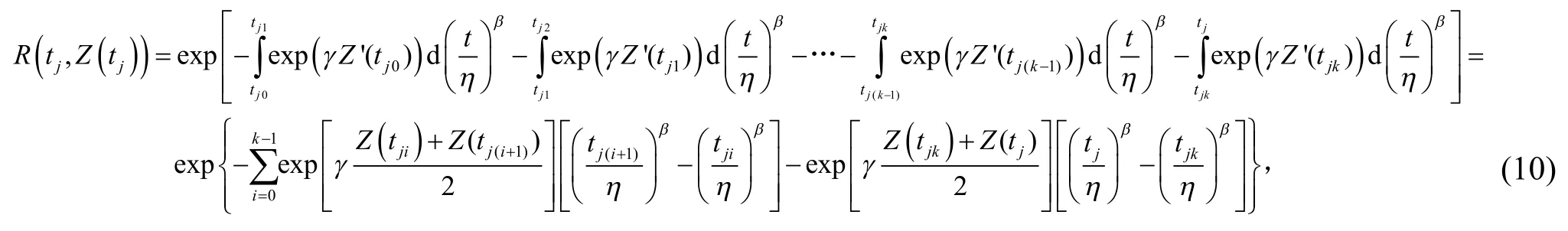
式(10)中，k為部件失效或截止時間前的檢測次數，tj為部件j失效或截止時間，tji為部件j第i次檢測時間，將式(7)、(10)代入式(6)，并兩邊取對數得

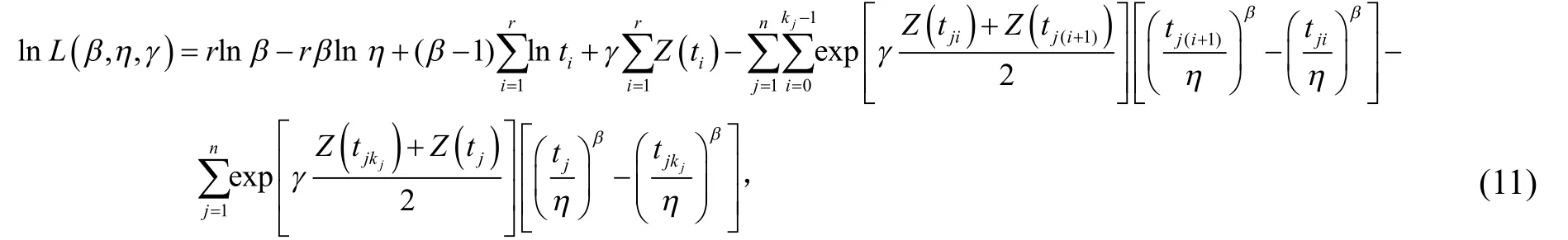
式(11)中，kj為部件j在失效或截止時間前的檢測次數。對數似然函數lnL(β,η,γ)與似然函數L(β,η,γ)具有同樣的增減性，對數似然函數取得最大值時的β*、η*和γ*也是似然函數的最大值點。在此采用具有快速收斂性的牛頓法進行求解[22]。首先將式(11)分別對β、η和γ求偏導數，令

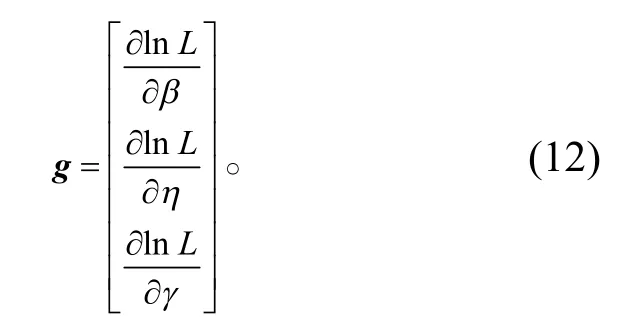
再對一階偏導數求二階偏導數，得到Hesse 矩陣如下：

用牛頓法構造迭代公式：

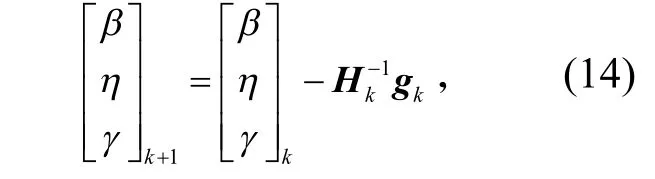
式(14)中，k為迭代次數，當k=0 時，β0、η0和γ0為初始值，設定初始值后由迭代公式即可求出參數估計值。

2 基于狀態的機會維修決策

2.1 機會維修策略

在制定維修決策時，首先確定維修要達到的目標，通常是要求部件達到最大可用度、最小維修費用率或安全性等目標。對于關鍵部件，一旦發生故障會產生嚴重后果，所以首要考慮安全性，即保證部件可靠度在最低可靠度要求值以上。滿足下式

式(15)中，Rp為最低可靠度要求，當部件可靠度小于Rp時即進行預防性維修。由于對船舶部件進行預防性維修時會產生停機損失費、固定維修成本以及機會損失成本，為減少這類損失，盡可能將多個部件進行集中維修，在有部件做預防性維修時，可對可靠度符合下式的其他部件進行適當的機會維修。

式(16)中，Ro為部件的機會維修可靠度閥值。基于狀態的機會維修決策過程如圖2。

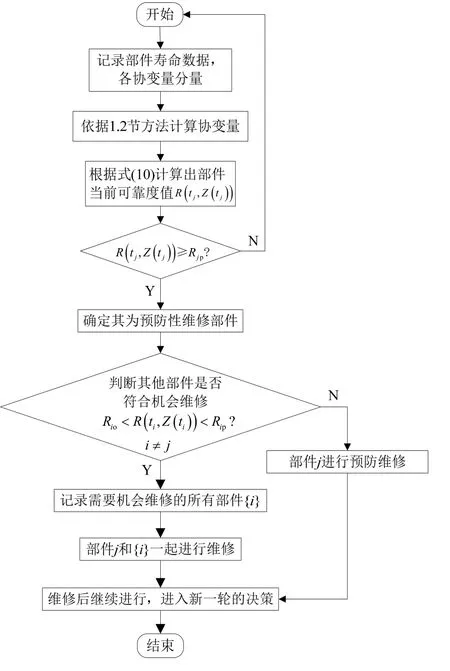
圖2 狀態機會維修決策流程Fig.2 Status opportunity maintenance decision process

2.2 船舶關鍵部件維修費用率

在船舶關鍵部件的狀態機會維修過程中，如出現非預期故障，則對部件進行故障維修，在觀察周期內，部件i總維修費用為

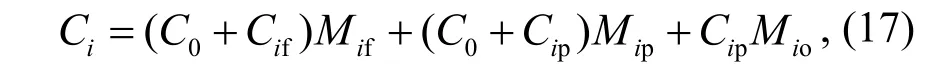
式(17)中，C0為固定維修費用，Cif為部件i的故障維修費用，Cip為部件i的預防性維修費用，Mif為部件i在觀察周期內的故障維修次數，Mip為部件i在觀察周期內的預防性維修次數，Mio為部件i在觀察周期內的機會維修次數。

在觀察周期內，船舶關鍵部件的總維修費用率為

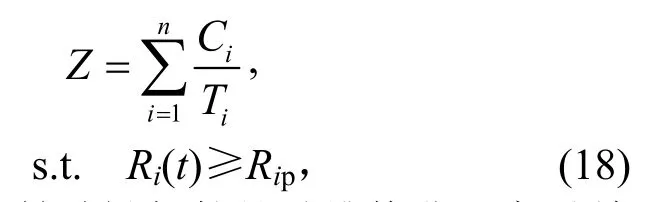
式(18)中，Z為船舶關鍵部件的總維修費用率（單位：元/ d），Ti為部件i各維修間隔期總和，n為船舶關鍵部件總數，Ri(t)為部件i在時刻t的可靠度，Rip為部件i的最低可靠度要求。

3 實例分析與討論

3.1 船舶關鍵部件參數

利用調研某船舶維修公司得到的船舶維修數據，對某型船舶主傳動系統的齒輪箱、尾軸前軸承和后軸承3 個關鍵部件進行分析，其中齒輪箱裝有溫度計，部分安裝有振動傳感器，水潤滑軸承的水冷卻系統管路裝有壓力表作為監測儀器，實時監測各部件的工作狀態。通過對各部件狀態數據、維修記錄、運行工況等信息收集整理后，運用1.2 節方法計算各部件壽命時間點的協變量，先利用層次分析法計算得到各部件協變量權重分配（表6），再應用式(4)計算得到部件各時刻的協變量。其中各部件壽命或監測終點與相應協變量數據見表7—9。

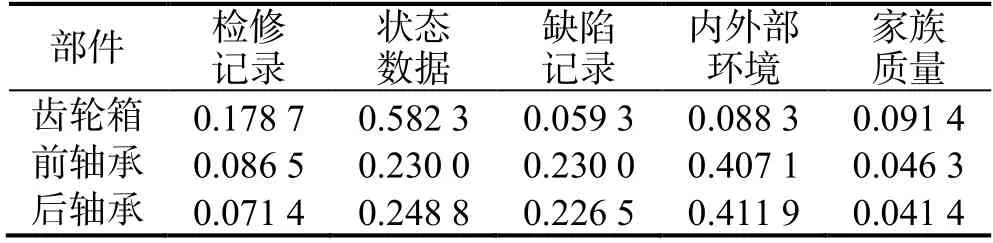
表6 各部件協變量權重Table 6 Weight of the covariates of each component

表7 齒輪箱壽命及協變量Table 7 Gearbox life and covariates

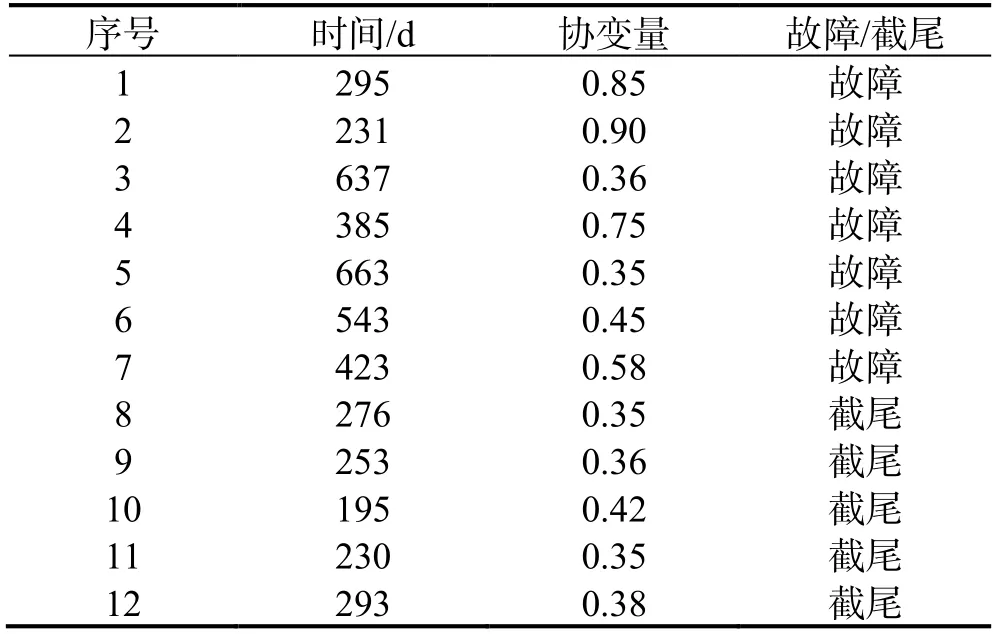
表8 尾軸前軸承壽命及協變量Table 8 Tailshaft front bearing life and covariates

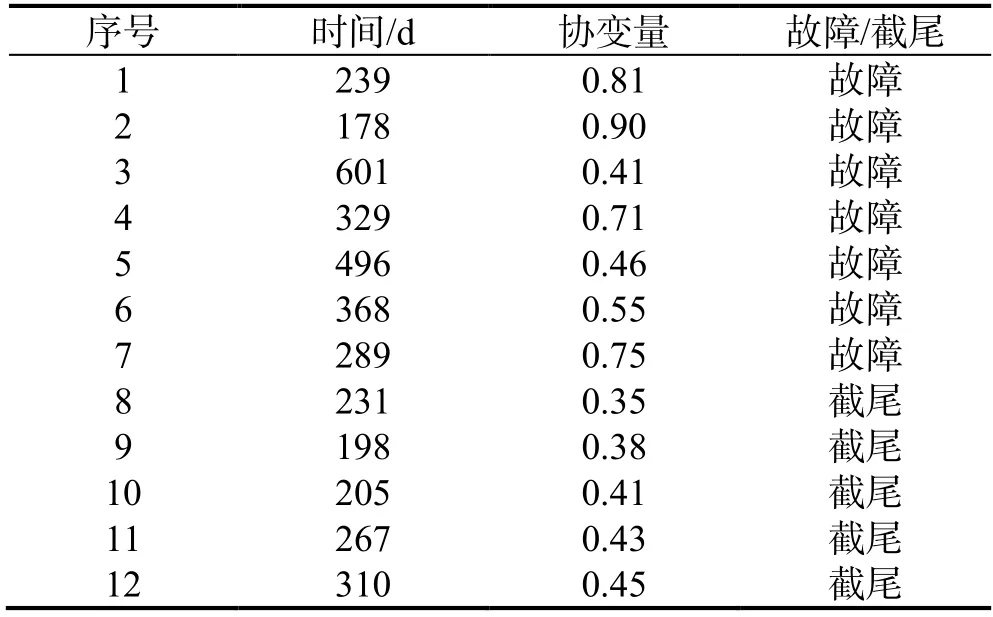
表9 尾軸后軸承壽命及協變量Table 9 Tailshaft rear bearing life and covariates

可看出，部件在各個時間點都有相對應的協變量，故障時間較早的部件協變量也相應較大，表示其安全隱患較大，壽命較短，反之亦然。根據式(14)，利用MATLAB R2016a 編程仿真，得到三個部件的參數估計值（表10）。

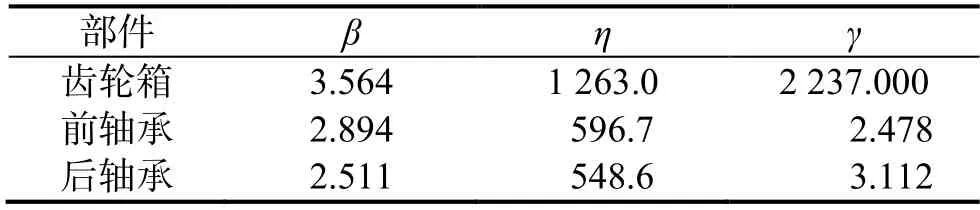
表10 各部件參數估計值Table 10 Estimated parameters of each component

3.2 船舶關鍵部件機會維修策略

齒輪箱、尾軸前軸承和后軸承屬于船舶主傳動系統的關鍵部件，其安全性有較高要求，其最低可靠度要求分別為0.80、0.75、0.75，設定機會維修可靠度閥值后可按第2 節介紹的方法對各部件進行預防性機會維修。本研究利用一組部件壽命和狀態數據為例進行說明，各部件可靠度變化趨勢見圖3—5。

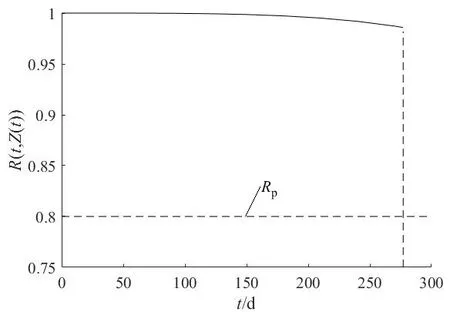
圖3 齒輪箱可靠度變化Fig.3 Gearbox reliability variation diagram

由可靠度的累積表達式(10)可知，依次記錄各監測時間點的協變量即可求得部件在各監測點的可靠度，當某部件可靠度降低到接近其最低可靠度要求時，可適當縮短監測周期。本研究中，在船舶運行到277 d 時，尾軸后軸承可靠度降低到預防性維修可靠度閥值處（圖5）；同時，尾軸前軸承可靠度處于其機會維修區間（圖4），為減少部件裝拆等固定維修成本和停機次數，可將前軸承和后軸承一起進行維修；而齒輪箱的可靠度處于機會維修可靠度閥值上方（圖3），故無需維修。

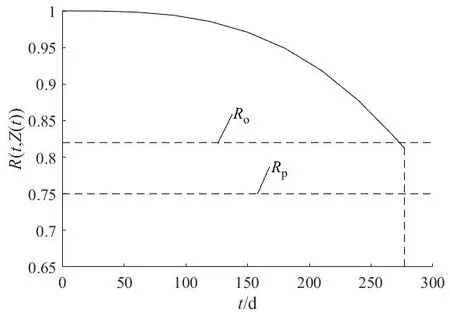
圖4 前軸承可靠度變化Fig.4 Front bearing reliability variation diagram

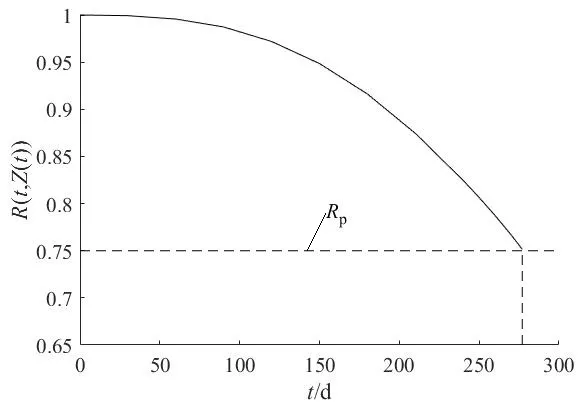
圖5 后軸承可靠度變化Fig.5 Rear bearing reliability variation diagram

3.3 船舶關鍵部件維修策略對比

為比較不同維修策略的優劣，將本研究模型與船舶關鍵部件傳統預防性維修策略、狀態預防維修策略和協變量只考慮狀態數據的機會維修策略進行對比，分別編號1—4，優化各維修策略在觀察周期內的總維修費用率。表11 為某船舶修造公司同型號船的各部件單次維修平均費用。

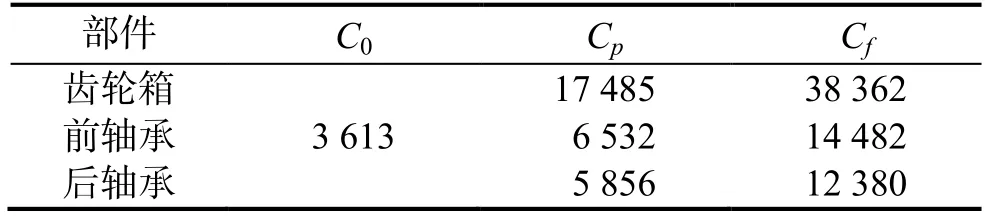
表11 船舶關鍵部件的維修費用Table 11 Maintenance costs of ship’s key parts元

以調研收集到的數據作為分析對象，假定各部件按順序依次進行維修或更換，以結束時間最短的部件壽命累加為觀察周期，本研究后軸承的累加壽命為最短，當第12 個軸承進行維修后不再進行觀察。其中，傳統預防性維修策略以定期維修或更新為主，輔以故障修的方式，其維修周期在維修費用率最小化后可得。狀態預防維修策略只考慮各部件的單獨維修，以部件最低可靠度為閥值，對各部件進行預防性維修[23]，而不考慮不同部件維修之間的經濟相關性，即機會維修。而協變量只考慮狀態數據的機會維修的策略，協變量只計算可觀察到的儀表上的狀態數據，如溫度、振動、壓力等，不考慮家族質量和維修記錄等前期數據，具體計算方法可參考文獻[13-14]。表12 為各維修策略的優化結果，表中各維修次數為系統總維修次數。

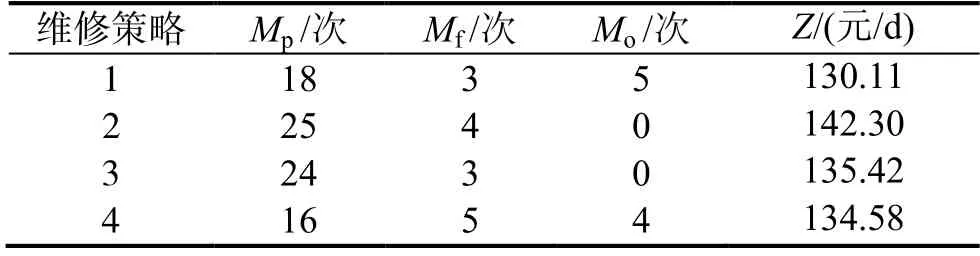
表12 各維修策略的優化結果Table 12 Optimization results of each maintenance strategy

傳統預防性維修根據各部件的整體壽命規律執行定周期維修，缺乏對具體部件狀態的考慮，容易造成對較健康部件的過度維修，而對前期缺陷較嚴重的部件又不能及時維修。狀態預防維修策略不考慮部件間的機會維修，容易造成固定維修費用和停機損失的增加。而協變量只考慮狀態數據的機會維修策略，容易對部件前期狀態較差的部件欠考慮，所以其預防性維修次數相對較少，而故障維修次數反而偏多。

本研究建立的狀態機會維修模型，其協變量考慮多個因素，故能更好地反映部件具體狀態和整體壽命規律，從而能有效避免維修過剩和維修不足。而部件之間的機會維修可節約固定維修成本和停機次數，提高船舶的在線運營率。

4 結論

1）充分考慮檢修記錄、家族質量史、缺陷記錄、內外部環境和狀態信息對船舶關鍵部件的壽命影響，運用具有主客觀分析方法優點的層次分析法計算各指標的權重。同時研究協變量在每個檢測周期的變化規律，選取每個檢測周期首尾兩個檢測點的協變量平均值作為該周期的協變量。在此基礎上建立兼顧部件壽命規律和個體狀態的比例風險模型，最后用極大似然估計法估計模型的3 個未知參數。

2）由部件壽命周期各檢測點的協變量，運用可靠度的累積表達式容易計算出部件在各檢測點的可靠度。根據各部件的最低可靠度要求，設定機會維修可靠度閥值，通過對比各部件的可靠度變化關系，引入狀態機會維修策略，可以降低船舶的固定維修費用和停機損失。以船舶齒輪箱、尾軸前軸承和后軸承為例，對比分析了四種維修策略，結果表明，本文提出的模型與其余三種維修策略相比，分別可以節省9.4%、4.1%、3.4%的維修費用。本研究建立的比例風險模型，其協變量的計算具有一定的主觀性，較大程度上依賴于決策者的經驗和技術水平，今后的研究可從建立更科學和客觀的協變量分析計算方法著手，提升模型的易用性。