非線性演化方程的切對(duì)稱群分析
高曉潤(rùn),黃晴
(西北大學(xué)數(shù)學(xué)學(xué)院,陜西 西安 710127)
1 引言
眾所周知,李群理論是分析偏微分方程的一種通用和便捷的工具.它最主要的應(yīng)用之一就是求解偏微分方程的不變解.因此,應(yīng)用李群理論對(duì)偏微分方程進(jìn)行群分類及進(jìn)一步的精確求解問(wèn)題引起了人們的廣泛關(guān)注.只依賴自變量和因變量的變換,稱之為點(diǎn)變換.更一般的,還依賴于因變量導(dǎo)數(shù)的變換,稱為廣義變換.特殊的,若變換依賴于自變量、因變量和因變量的一階導(dǎo)數(shù),則稱之為切變換.目前,人們已經(jīng)對(duì)點(diǎn)變換有了廣泛且深刻的研究[1-2],而關(guān)于切變換的研究卻比較少.
十九世紀(jì)數(shù)學(xué)家Sophus Lie(1842-1899)提出和發(fā)展了李群方法.此后,李群算法被認(rèn)為是分析偏微分方程最強(qiáng)大的工具之一,主要原因是該方法可以減少變量數(shù)目,有可能導(dǎo)出與偏微分方程相關(guān)的群不變解,而且它也推動(dòng)了其它數(shù)學(xué)物理方法的發(fā)展[3].
雖然關(guān)于廣義對(duì)稱的研究不多,但是近年來(lái)廣義對(duì)稱,尤其是切對(duì)稱,受到了越來(lái)越多的關(guān)注.目前在切對(duì)稱領(lǐng)域一些學(xué)者也做了許多工作.例如文獻(xiàn)[4]使用二階偏微分方程的切變換來(lái)求得這些方程的偽不變解.文獻(xiàn)[5]將切變換應(yīng)用于三階常微分方程從而得到隱變換.在文獻(xiàn)[6]中一些切變換也被認(rèn)為是偏微分方程的隱對(duì)稱的新起源.本文將優(yōu)化系統(tǒng)的概念應(yīng)用于切對(duì)稱,提出一種代數(shù)分類算法.并以下面的二階非線性演化方程為例:

給出它所容許的切對(duì)稱并建立切對(duì)稱的一維優(yōu)化系統(tǒng),然后進(jìn)行對(duì)稱約化,從而得到一些約化方程和群不變解.
眾所周知切對(duì)稱等價(jià)于一階廣義對(duì)稱.
定理1.1[1]如果一個(gè)廣義變換的無(wú)窮小生成子具有以下形式

那么它等價(jià)于一個(gè)切變換且該切變換的無(wú)窮小生成子形式如下

2 方程 (1)的切對(duì)稱群分析
根據(jù)廣義對(duì)稱無(wú)窮小生成準(zhǔn)則[1],可以得到方程(1)的切對(duì)稱群.它由以下5個(gè)生成函數(shù)對(duì)應(yīng)的向量場(chǎng)張成:
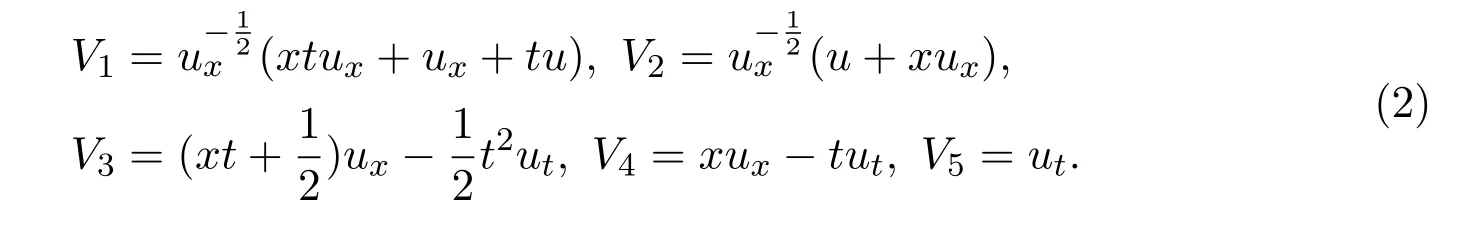
兩個(gè)切對(duì)稱生成子的交換關(guān)系由以下公式給出[7]
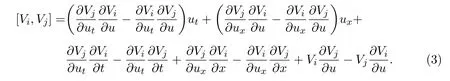
基于這個(gè)公式,計(jì)算V1,V2,···,V5之間的所有交換關(guān)系,并將結(jié)果列在表 1中,其中(i,j)項(xiàng)表示交換子[Vi,Vj].

表1 代數(shù)(2)的交換子表
伴隨表示由李級(jí)數(shù)
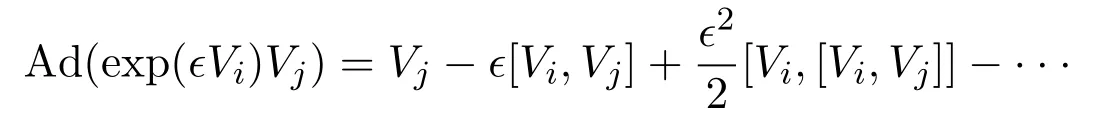
給出,其中[Vi,Vj]表示交換子(3),?表示參數(shù).表2給出了代數(shù)(2)的所有伴隨表示,其中 (i,j)項(xiàng)表示 Ad(exp(?Vi)Vj).

表2 代數(shù)(2)的伴隨表示
給定方程所容許的切對(duì)稱群有無(wú)窮多個(gè)子群,且任意無(wú)窮小生成子的線性組合還是無(wú)窮小生成子.為了能夠不處理無(wú)窮多的切對(duì)稱并完整準(zhǔn)確地給出所研究方程的約化方程和不變解,需要得到切對(duì)稱群的所有不等價(jià)子群,即建立切對(duì)稱群的優(yōu)化系統(tǒng).
定理 2.1代數(shù)(2)的一維優(yōu)化系統(tǒng)為

證明取V的最一般形式V=a1V1+a2V2+a3V3+a4V4+a5V5.接下來(lái)利用合適的伴隨表示來(lái)簡(jiǎn)化它.將伴隨表示Ad(exp(?1V3))與Ad(exp(?2V5))作用在V上,可以得到



當(dāng)令?9=1,?10=?2時(shí),顯然有V1與V2等價(jià).所以可得V等價(jià)于V2.
現(xiàn)在已經(jīng)證明了代數(shù) (2)的任何一維子空間都等價(jià)于定理 2.1中由W1,···,W6張成的子空間之一.為了完成定理2.1的證明,將借助不變量或半不變量[8]來(lái)說(shuō)明代數(shù)(4)中任意兩個(gè)代數(shù)是相互不等價(jià)的.
引理 2.1是不變量.
證明通過(guò)計(jì)算,可以得到代數(shù)(2)的基靈型.易知在伴隨作用下基靈型是不變的.
引理2.2定義

那么B,C是不變量.
證明從表2容易看出B與C是不變量.
現(xiàn)在,根據(jù)代數(shù) (4)中的每一個(gè)Wi(i=1,···,6),可以確定不變量A,B和C,并將結(jié)果列在表3中.

表3 代數(shù)(4)的不變量
從表3易知每個(gè)Wi(i=1,···,6)都是不等價(jià)的.
3 方程(1)的對(duì)稱約化和群不變解
此節(jié)將利用方程(1)的一維優(yōu)化系統(tǒng),對(duì)方程(1)進(jìn)行對(duì)稱約化,并給出相應(yīng)的約化方程和不變解.


其中z=xt2+2x+t.

該情形中的方程求解比較困難,但是可以知道這是方程(1)的不變解在該分類下所必須要滿足的條件.
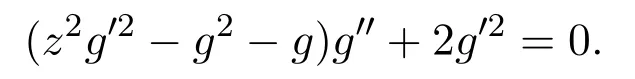

g′(t)=0.
因此有g(shù)(t)=c.故方程(1)有不變解

4 結(jié)論
本文研究了優(yōu)化系統(tǒng)在切對(duì)稱方面的應(yīng)用,并以二階非線性演化方程(1)為例,計(jì)算了它的切對(duì)稱并建立了切對(duì)稱的優(yōu)化系統(tǒng).然后根據(jù)優(yōu)化系統(tǒng)中的等價(jià)分類,對(duì)方程進(jìn)行了對(duì)稱約化,并在此基礎(chǔ)上獲得了一些約化方程和精確解.

