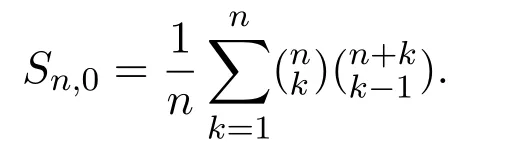加權廣義的Schr?der路的計數
馬帥帥,楊勝良
(蘭州理工大學理學院,甘肅 蘭州 730050)
1 引言
Schr?der數[1-5]是一種常見的組合數,在有序樹、整數的拆分等問題中有廣泛應用.文獻 [1]給出了 Schr?der數的相關解釋:半長為n的 Schr?der路是從 (0,0)到(2n,0)的一條始終保持在x軸上方的經過整點的格路徑,允許的步集為上步U=(1,1),水平步H=(2,0)以及下步D=(1,?1).在x軸沒有水平步的 Schr?der路被稱為小 Schr?der 路.
所有半長為n的 Schr?der路的個數是 Schr?der數,記為rn,Schr?der數的發生函數r(t)滿足等式
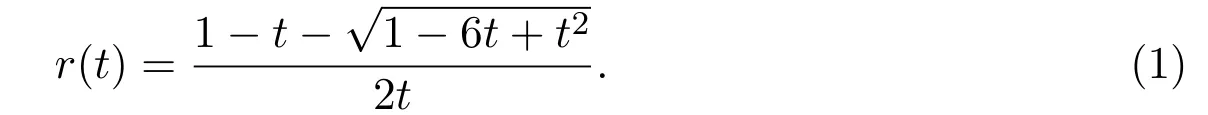
所有半長為n的小 Schr?der路的個數是小 Schr?der數,記作sn,小 Schr?der 數的發生函數s(t)滿足等式
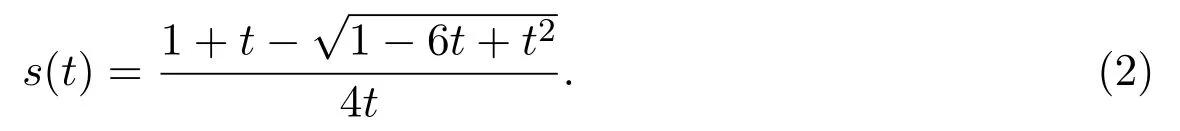
定義 1.1步集為u=(1,1),h=(2,0),d1=(3,?1),d2=(2,?2)并且權分別為1,a,b,c的始終保持在x軸上方的格路徑,稱之為加權廣義的Schr?der路.
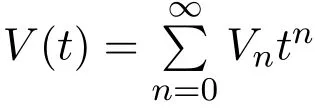

圖1 符號化方法
由符號化方法可以得到這種路的發生函數為
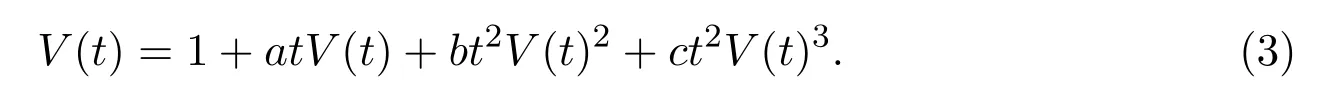
若a=2,并且b=c=1時,對應的發生函數為
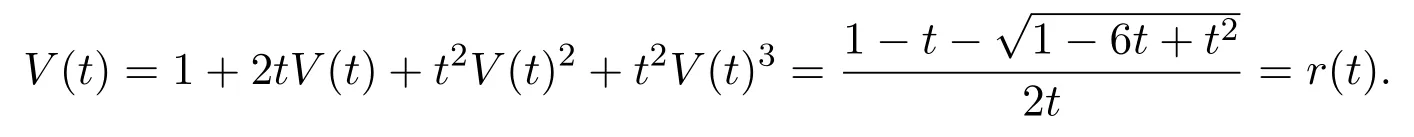
由此可以得到 Schr?der數的發生函數,那么這種從 (0,0)到(2n,0),步集為u=(1,1),h=(2,0),d1=(3,?1),d2=(2,?2)并且權分別為1,2,1,1的始終保持在x軸上方的格路徑是Schr?der數又一種新的組合解釋.
若a=3,b=2,c=0時,對應的發生函數S(t)為
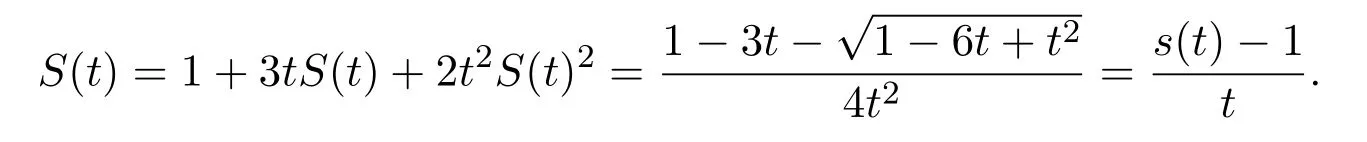
由此可以得到用小Schr?der數的發生函數表達的式子,那么這種從(0,0)到(2n,0),步集為u=(1,1),h=(2,0),d1=(3,?1),d2=(2,?2)并且權分別為 1,3,2,0的始終保持在x軸上方的格路徑是小Schr?der數又一種新的組合解釋.
本文用矩陣的方法研究組合問題,下面是Riordan矩陣的相關概念.
定義1.2[6]若無限下三角矩陣M=(mn,k)n,k∈N第k列的生成函數為g(t)f(t)k則稱該矩陣為Riordan矩陣,其中
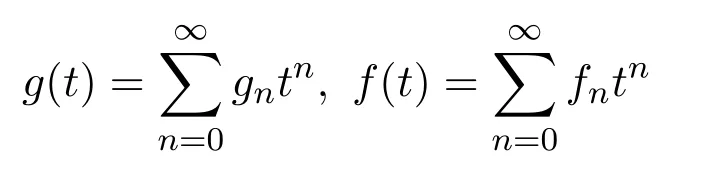
是形式冪級數,且d00,f0=0,f10,記mn,k=[tn]g(t)f(t)k,其中 [tn]是系數算子,記作M=(g(t),f(t))=(g,f).

2 加權廣義的 Schr?der 路和 Schr?der 數
本節用加權廣義的Schr?der路給Schr?der數一個新的組合解釋.令V(n,k)表示從(0,0)到(2n?k,k)的始終保持在x軸上方格路的集合,其中格路的步集為u=(1,1),h=(2,0),d1=(3,?1),d2=(2,?2),并且權分別為 1,2,1,1,則有Vn.k=|V(n,k)|.它的構造方法如圖2所示.
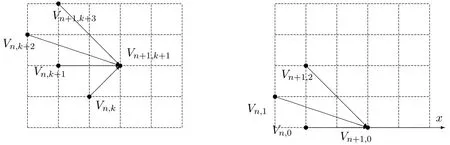
圖2 矩陣V的遞推關系
由圖2可知Vn,k滿足如下遞推關系,
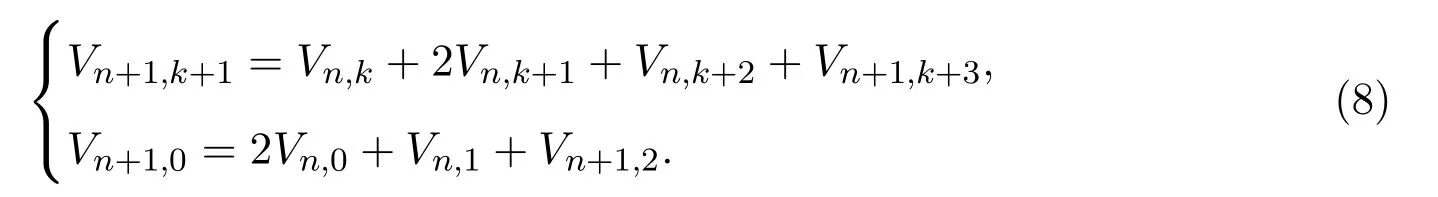
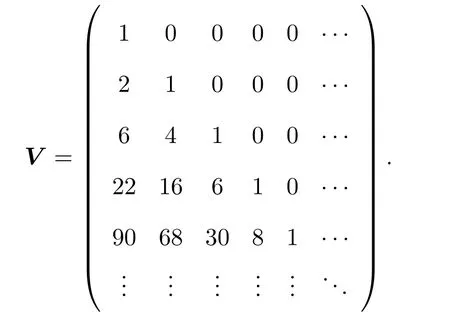
矩陣V=(Vn,k)n,k≥0的第 0列就是 Schr?der數序列 (見文獻 [8]中序列A006318),通項公式有
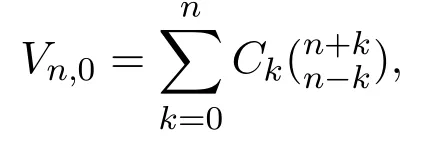
其中Ck是第k個Catalan數[9].
因為Vn+1,k+1=Vn,k+2Vn,k+1+Vn,k+2+Vn+1,k+3,對應的A-矩陣為
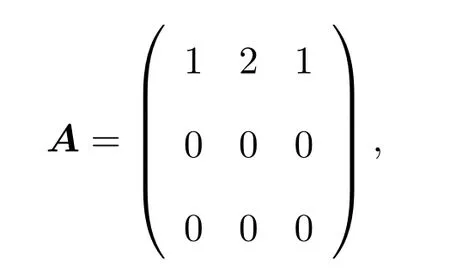
且Φ[0](t)=1+2t+t2.根據(5)式可得
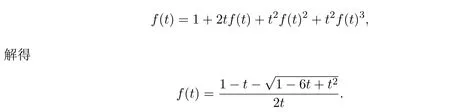
又因為Vn+1,0=2Vn,0+Vn,1+Vn+1,2,所以R[0](t)=2+t,S[1](t)=t.根據(7)式可得
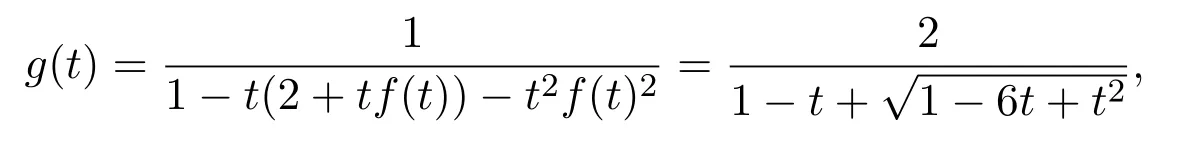
則可得如下定理.
定理 2.1設V(n,k)表示從(0,0)到(2n?k,k)的始終保持在x軸上方格路的集合,其中格路的步集為u=(1,1),h=(2,0),d1=(3,?1),d2=(2,?2),并且權分別為1,2,1,1,則矩陣V可以表示為Riordan矩陣
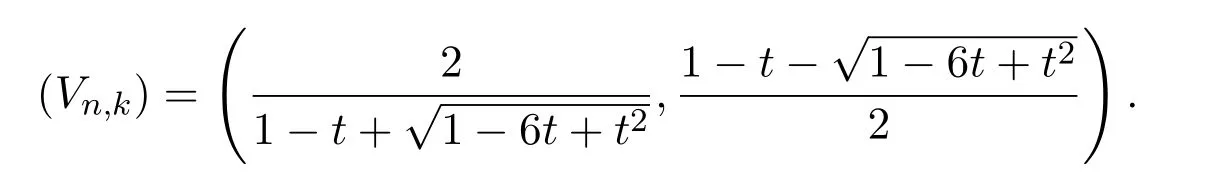
若令U(n,k)表示從 (0,0)到 (2n?k,k)的格路的集合,其中格路允許的步集為u=(1,1),h=(2,0),d1=(3,?1),d2=(2,?2),并且權分別為 1,2,1,1,則有Un.k=|U(n,k)|.這種不限制在x軸上方的路是自由的,它的發生函數可以表示為

其中Ci(t)是矩陣U第i列的發生函數,可得
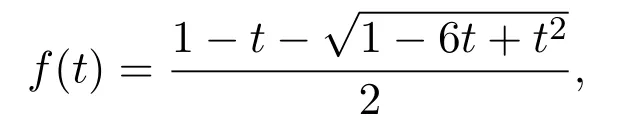
則可得如下定理.
定理 2.2設U(n,k)表示從(0,0)到(2n?k,k)的格路的集合,其中格路允許的步集為u=(1,1),h=(2,0),d1=(3,?1),d2=(2,?2),并且權分別為 1,2,1,1,則矩陣U可以表示為Riordan矩陣
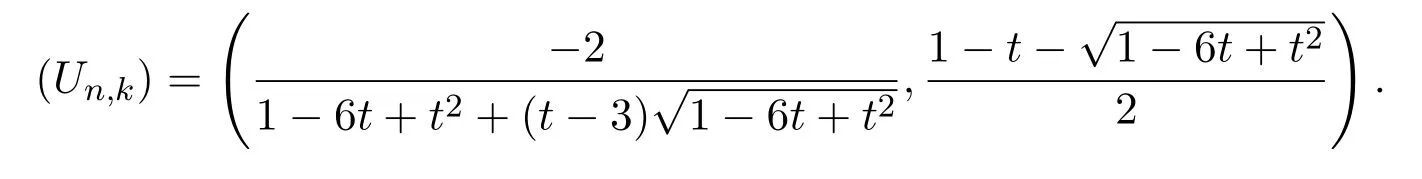
3 加權廣義的 Schr?der路和小 Schr?der數
本節用加權廣義的Schr?der路給小Schr?der數一個新的組合解釋.現在在上一節給出的Schr?der數新的組合解釋中加一個在x軸沒有水平步的條件,使之成為一種特殊的路,用n表示這種路的集合,(t)表示n的發生函數.

圖3 符號化方法
根據符號化方法可以得到這種路的發生函數為
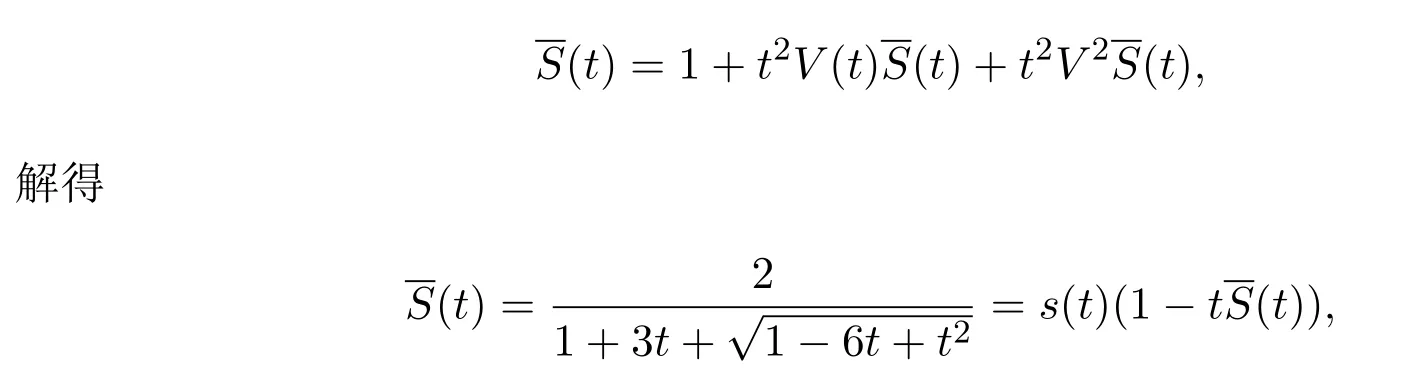
其中s(t)表示小 Schr?der路的發生函數,由(t)展開式前n項可以找到在OEIS的解釋為沒有山的小Schr?der路.那么這種從(0,0)到(2n,0)允許的步集為
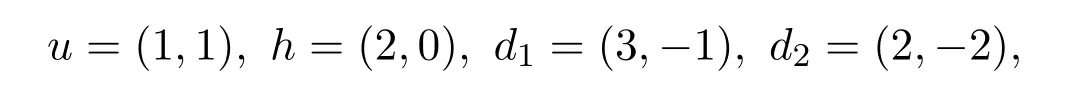
其中權分別為1,2,1,1,且在x軸沒有水平步h=(2,0)的始終保持在x軸上方的格路徑,就是沒有山的小Schr?der路的又一種新的組合解釋.令(n,k)表示這種路的集合,則有.它的構造方法如圖所示:
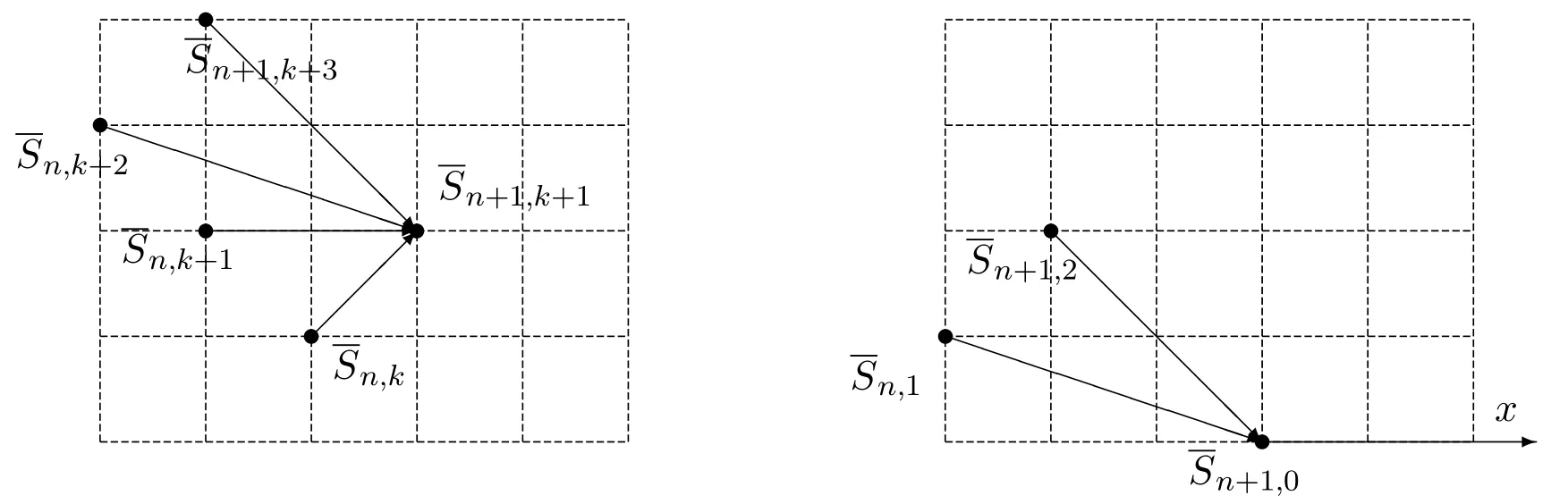
圖4 矩陣的遞推關系
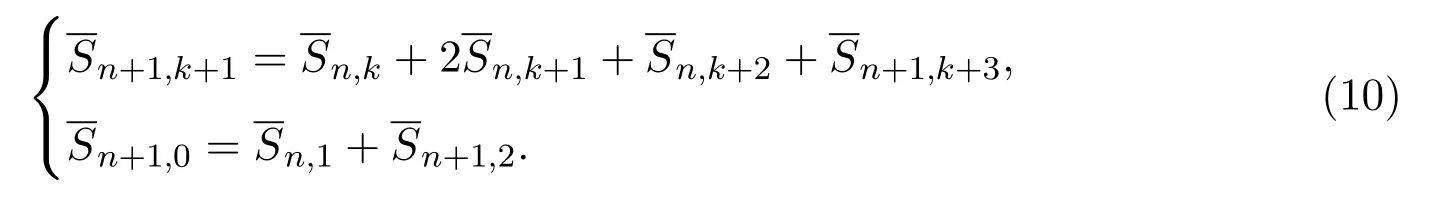


令S(n,k)表示從(0,0)到(2n?k,k)的始終保持在x軸上方格路的集合,其中格路的步集為u=(1,1),h=(2,0),d1=(3,?1),d2=(2,?2),并且權分別為 1,3,2,0,則有Sn.k=|S(n,k)|.它的構造方法如圖所示:
由圖5可知Sn,k滿足如下遞推關系,
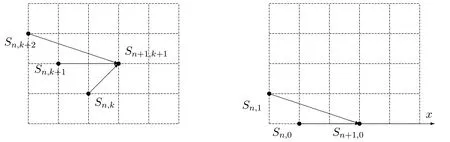
圖5 矩陣S的遞推關系
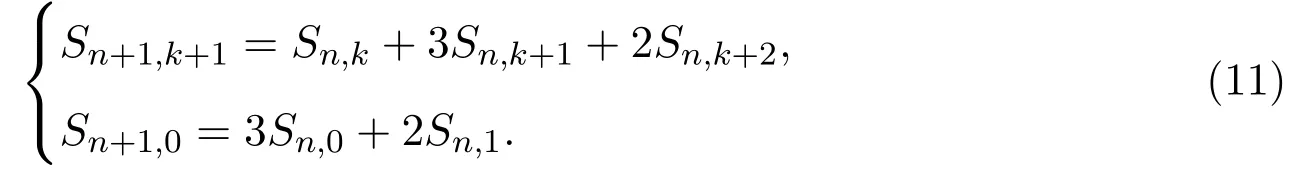
矩陣S=(Sn,k)n,k≥0的第 0列就是小 Schr?der數序列 (見文獻 [8]中序列A001003),其中通項公式有