擴散Beddington-DeAngelis捕食食餌模型的行波解

劉欣然,肖海濱

(寧波大學數學與統計學院,浙江 寧波 315211)

1 引言

有界行波解是演化PDE一類描述空間狀態平移過程的不變解,具有形式

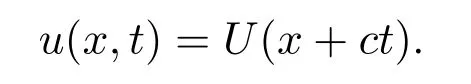
行波解在諸多領域,比如生態種群動力學,燃燒理論,生化反應,疾病傳播等,具有廣泛的應用.擴散捕食-食餌生態系統的行波解是生物數學研究的一個非常重要的主題,近幾十年來一直吸引國內外眾多學者的廣泛關注,已有大量的研究成果[1-6].當捕食者與食餌間的功能反應函數不依賴捕食者的種群密度時,擴散捕食食餌模型的非負行波解的研究框架較為完整.一般的功能反應的擴散捕食食餌模型可描述為拋物型方程組:

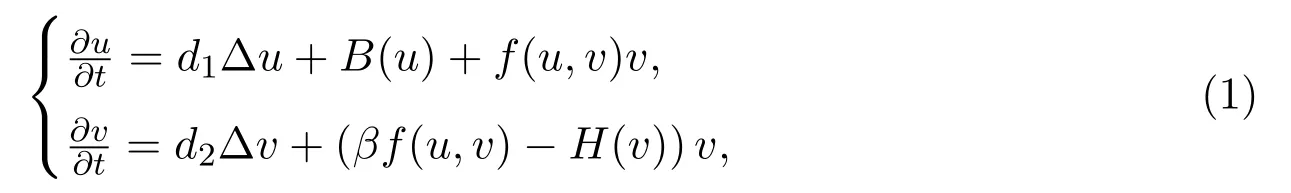
其中u(x,t),v(x,t)分別為食餌和捕食者的種群密度,Δ是Laplace算子,正數d1,d2分別為食餌和捕食者在空間上各自的擴散系數,B(u),?H(v)v分別稱為食餌和捕食者的增長函數,f(u,v)稱為捕食者對食餌的功能反應函數,而常數β稱為二者相互作用的轉化系數.

當系統(1)的功能反應函數不依賴捕食者種群密度時,其行波解的研究相對比較完整,Dunbar是研究捕食-食餌擴散系統行波解的先鋒.在忽視食餌擴散和考慮食餌擴散的情況下,基于 Wazewski原理和LaSalle不變原理,文獻[7-8]應用拓撲打靶方法分別證明:LotKa-Volterra微分方程模型存在連結邊界平衡點到共存平衡點的非負行波解.文獻[9]又進一步研究了功能反應函數為Holling-Ⅱ型的擴散捕食食餌模型,結合Hopf分支理論,證明了連結邊界平衡點到周期軌道的非負行波解的存在性.與此同時,文獻[10]應用連結指標理論研究捕食系統的行波解.文獻[11]進而綜合應用Conley指標,連續性理論和連結矩陣理論,對一類抽象捕食系統建立了各種不同類型的行波解.后來,文獻[12-13]基于Dunbar的研究方法和Hopf分支理論分別研究了Holling-Ⅱ型和Holling-III型的捕食系統連結兩個平衡點的行波解和小振幅周期波鏈的存在性.最近十年來,捕食生態系統的行波解仍為應用數學研究工作者的熱點主題,涌現出不少重要的研究成果.如有別于眾多文獻的不同之處,基于有界Wazewski集的構造,文獻[14]研究了Sigmoidal型的捕食系統的連結邊界平衡點到共存平衡點和原點到共存平衡點的行波解,推廣了相關文獻的結果.文獻[15]應用文獻[8]的思想方法研究了具有一般增長函數的擴散Gauss型的捕食系統的行波解,推廣了眾多文獻的相關結論.文獻[16]借助于獨特的Wazewski集的構造,在忽視食餌擴散和功能反應函數缺少單調性假設的情形下,研究了擴散捕食模型

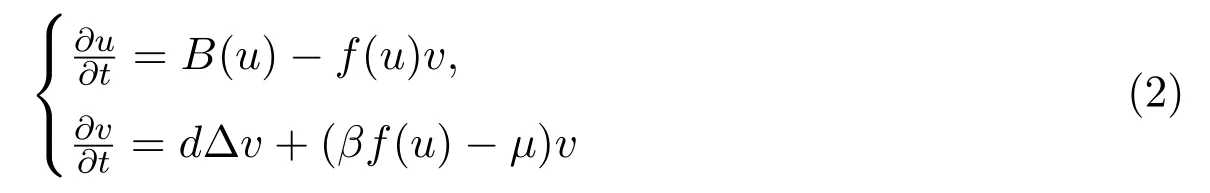
連結邊界平衡點到共存平衡點的行波解.據筆者目前所知,文獻[16]的結果是對較為一般的上述系統在較為弱的且具有生態意義條件下獲得的最優結果.最近,文獻[17]進一步考慮了捕食種群具有非線性密度限制的捕食模型,指出文獻[16]的結果在這種密度制約下可以保持.

當系統 (1)的功能反應函數依賴捕食者種群密度時,現有文獻對其行波解的研究相對比較零散,反應函數主要集中為 Beddington-DeAngelis型.文獻 [18]考察了食餌具有 Logistic增長,捕食者具有常死亡率的擴散Beddington-DeAngelis模型,應用文獻[7-8]的思想方法給出系統存在連結邊界平衡點到共存平衡點的非負行波解的充分條件及臨界波速.后來,文獻 [19]又進一步利用文獻 [16]的方法,把建立半連結軌道的方法推廣到功能反應函數依賴捕食種群密度的情形,并應用到具有線性密度制約的 Beddington-DeAngelis模型.接著,文獻 [20]總結文獻 [16],文獻 [19]的思想,把方法推廣到考慮食餌擴散的情形,即四維的行波系統,并應用到線性密度制約的Beddington-DeAngelis模型.

正如文獻[21-22]指出的那樣,不少種群特別是能量級別高的捕食種群的死亡因素不僅僅包括自然死亡,還存在種內競爭,人為破壞等.為此,為方便起見,本文將研究捕食者和食餌都具有一般非線性密度制約的一維擴散Beddington-DeAngelis模型

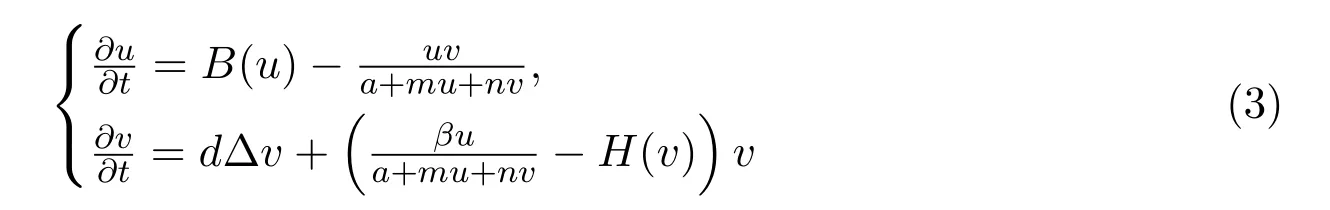
的非負行波解,其中B(u),?H(v)v分別稱為食餌和捕食者的增長函數,a,m,n均為正常數,正數d為捕食者的擴散系數,Δ是Laplace算子.具體的結構性假設將在下面給出.當B(u)=ru(1?u),H(v)=μ+δv時,系統(3)即為文獻[19]中討論的線性密度制約模型.

2 模型假設及主要結果

系統(3)的ODE系統如下:

2 基本準備

令u(x,t)=U(x+ct)=U(ξ),v(x,t)=V(x+ct)=V(ξ),代入系統 (3)得其行波系統

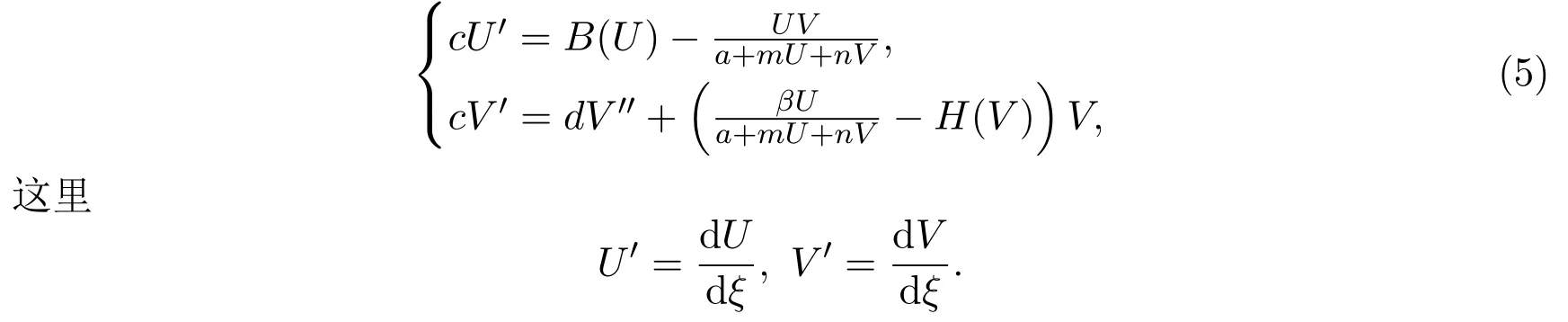
易知,(U(ξ),V(ξ))是系統 (5)的解當且僅當 (U(x+ct),V(x+ct))是系統 (3)的解.令cW=cV?dV′,將系統(5)轉化為與之等價的一階方程組

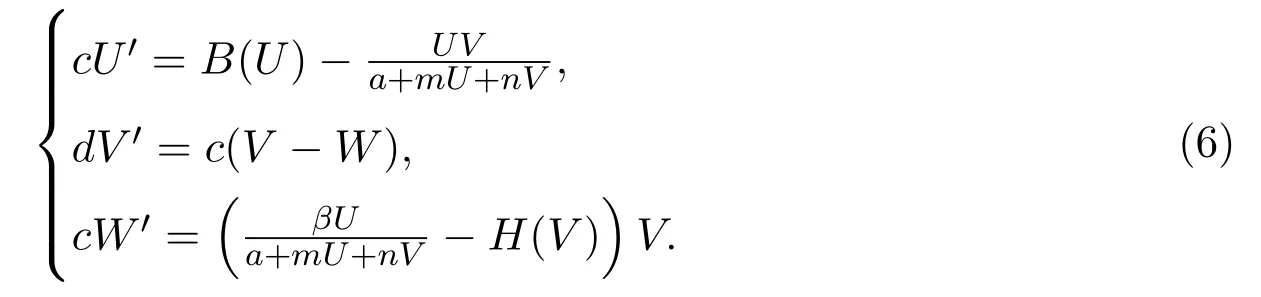
因此,(U(x+ct),V(x+ct))為系統(3)存在連結平衡點EK和E?的非負行波解當且僅當 (U(ξ),V(ξ),W(ξ)) 是系統 (6) 滿足U(ξ)≥0,V(ξ)≥0,?∞<ξ<+∞和邊界條件

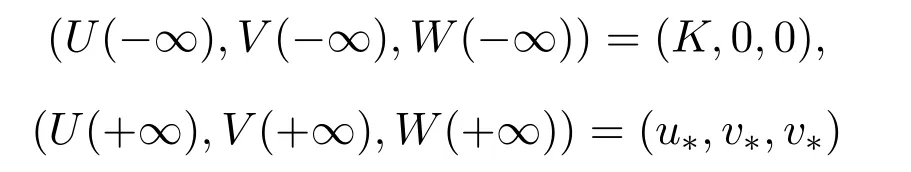
的解,即連結 (K,0,0)到 (u?,v?,v?)的軌道.由于數學符號表示的習慣,系統 (6)的時間ξ仍記為t.系統(6)在(K,0,0)處的線性化系統為

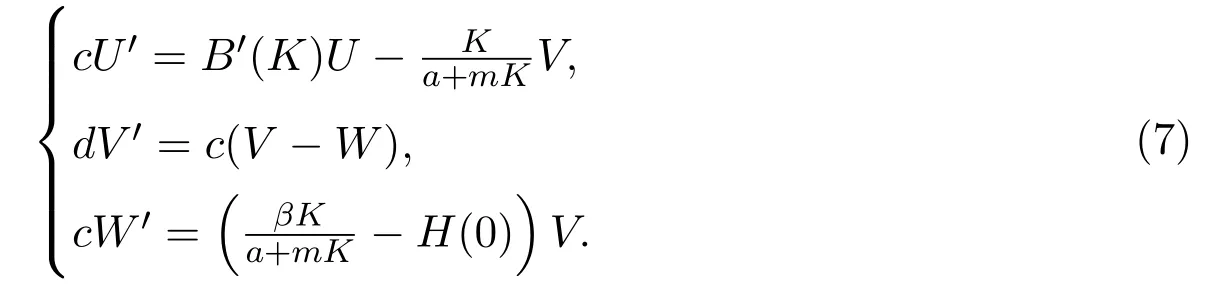
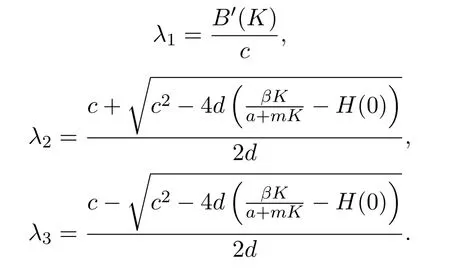
經過計算得到,其系數矩陣有三個特征值

3 定理1.1的證明

通過構造一個Wazewski集來獲得系統(6)以邊界平衡點(K,0,0)為α極限點的非負半軌道,并利用拓撲打靶法證明此半軌道以共存平衡點(u?,v?,v?)為ω極限點,來證得它即為系統(6)的連結(K,0,0)到(u?,v?,v?)的非負完全軌道.

3.1 Wazewski集的構造

3.2 不變軌道的存在性

本節研究系統(6)在Σ內的以平衡點(K,0,0)為α極限點的不變軌道的存在性.為此考慮研究系統(6)在(K,0,0)處的不穩定流形.系統(6)在(K,0,0)處的線性化系統(7)的特征值λ2,λ3,對應的特征向量分別為

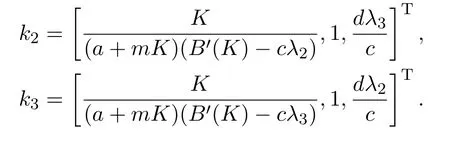
3.3 連結軌道的存在性

對引理3.2.2所建立的Σ內的軌道γ0,本文通過引入它的Lyapunov函數來獲得它的V,W分量的一致正有界性,進而證明γ0是連結平衡點 (K,0,0)和 (u?,v?,v?)的非負軌道.

4 總結與展望

基于國內外研究和生態學意義,本論文研究捕食者和食餌皆具有一般非線性密度制約的一維擴散Beddington-DeAngelis模型的行波解,把文獻[18]的捕食者和食餌皆具有線性密度制約的Beddington-DeAngelis模型的連結邊界平衡點到共存平衡點的行波解的存在性結果推廣到了一般非線性密度制約情形.盡管如此,系統(1)功能反應函數依賴捕食種群密度但非Beddington-DeAngelis型時,其行波解的研究仍面臨挑戰,國內外文獻涉足甚少.此外,當不能忽視食餌種群的擴散時,此時的行波系統是四維ODE系統,對于高維的行波系統,如何應用拓撲打靶法,建立系統的行波解有些難度,仍有待研究.