兩時滯廣義Logistic模型的Hopf分支與混沌

李順異, 熊梅,唐興蕓

(1.黔南民族師范學院數學與統計學院,貴州 都勻 558000;2.黔南民族師范學院數學與統計學院復雜系統與計算智能重點實驗室,貴州 都勻 558000)

1 引言

英國經濟學家,人口學家馬爾薩斯(Malthus)在其出版的《人口論》一書中,認為人口按照幾何級數增長,建立了著名的單種群增長模型N′(t)=rN(t),其中r為種群的凈增長率.考慮到環境因素對種群增長的影響,1838年比利時學者Verhulst提出了Logistic模型N′(t)=rN(t)[1?N(t)/Nm],其中Nm為環境容納量.種群的增長,不僅受到環境因素的影響,還受到種群內部相互作用的影響.種群內部的相互合作,如群體防衛,群體捕食等對種群的增長起著積極作用,而種群內部的相互競爭,如密度制約,擁擠效應等對種群的增長起著消極作用.種群內部的相互作用對種群的增長,不是立刻體現出來的,而是需要一定時間的,即種群內部的相互合作和競爭,對種群的增長有一定時間的滯后效應[1].

文獻[2]構建了時滯單種群模型[2]

其中b∈R,a>0,c>0.當b>0時,種群的競爭時滯與合作時滯是相同的τ,當b<0時,可視為對經典的時滯單種群Logistic的推廣.文獻[2]研究了模型(1.1)正解關于正平衡點N?振動性及正平衡點N?全局漸進吸引的充分條件.時滯作用是系統不穩定的一個重要因素,往往會使穩定的平衡點失穩而出現周期波動,進而出現更為復雜的動力學行為,如擬周期振動,混沌等[3-8].考慮到種群的競爭時滯與合作時滯不一定是相等的(τ1不一定等于τ2),即使只有競爭時滯作用,不同形式的競爭,其時滯也不一定相等.本文在模型(1.1)的基礎上構建兩時滯廣義Logistic模型

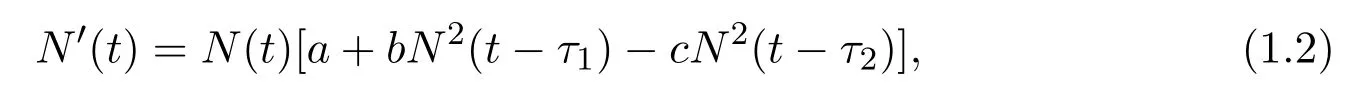
運用特征根方法研究模型正平衡點的穩定性,討論其發生局部Hopf分支和穩定性切換的條件,分析分支點關于系統參數的單調性和極限性質,并給出數值模擬佐證理論結果.

2 平衡點局部穩定性分析

模型(1.2)有唯一的正平衡點

其在N?處的線性化方程為

特征方程為

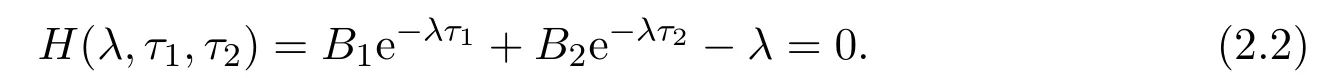
當τ1=τ2=0時,由方程 (2.2)得

由Routh-Hurwitz判別法知正平衡點局部穩定.

3 局部 Hopf分支分析

3.1 情形 1 τ1>0,τ2≡0.

3.2 情形 2 τ1≡0,τ2>0.

4 數值例子及結論

在模型(1.2)中,令a=2,c=2.5,N(0)=0.5,得b?=?2.5820.取b=?4.5b?,由情形 2得,τ1≡0,;取b=?0.9,由情形 3得,τ(0)=0.4702,都在N?附近發生 Hopf分支 (圖 1(b),(c)).

圖1 模型 (1.2)的動力學行為:(a)τ2≡0,,;(b) τ1 ≡ 0,,;(c)τ1≡ τ2= τ,τ=0.45< τ(0),τ=0.49> τ(0)

由分支值關于參數b的單調性和極限性質知

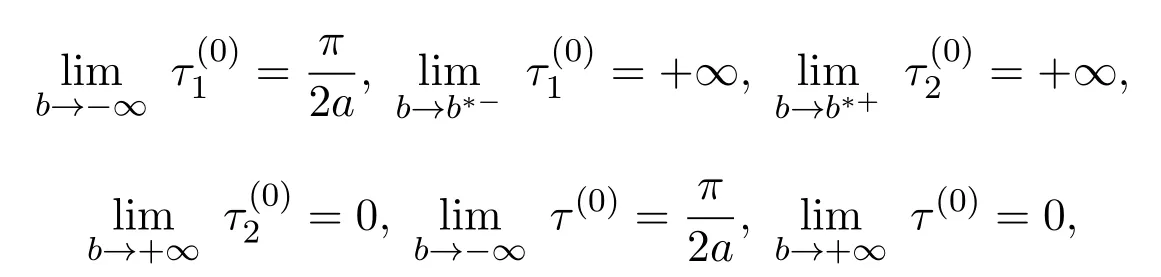
這表明情形1(bb?,τ1≡0)和情形 3(τ1≡τ2)對任何的正數τ?>0,都存在適當的參數b,使得τ=τ?成為第一分支值.情形 1(bb?)都屬于條件分支,分支值關于參數b的單調性相反;而情形2是無條件分支,分支值關于參數b嚴格單調遞減.

令b=?4.5,τ1=0.64∈Sτ1,由 (3.19)式得ω1=2.31838,ω2=1.88341,由 (3.20)式得分支值(圖2).

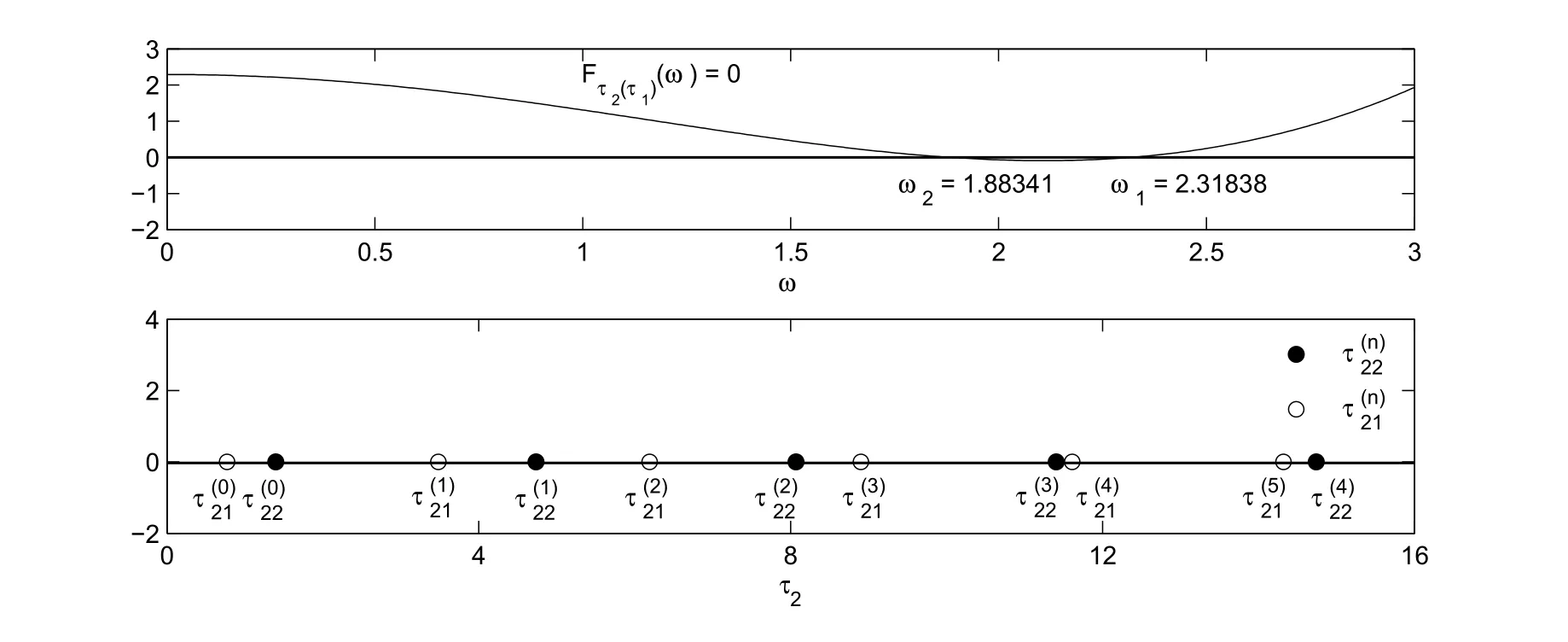
圖 2 Fτ2(τ1)(ω)=0 和分支值示意圖

關于τ2的局部穩定域由5個小區間構成,當τ1=0.64,τ2從0開始增加時,模型(1.2)將經歷5次穩定性切換,最終變得不穩定.

進一步,令b=1.5,當τ2=0.3時作出種群N(t)關于τ1在區間 [0.6,1.0]上變化的分支圖(圖3),由圖3知,模型經歷了倍周期分支到混沌的動力學行為(圖4).

圖 3 當 τ2=0.3時,種群N(t)關于 τ1的分支圖

圖4 當τ2=0.3時,模型(1.2)的典型動力學行為:τ1=0.7,0.78,0.82,1,2倍周期→4倍周期→8倍周期→混沌

本文基于種群內部相互競爭與合作的基本關系,構建了具有兩個離散時滯的廣義Logistic模型,詳細討論了各種情況下系統發生Hopf分支和穩定性切換的充分條件.數值例子展示了系統諸如穩定性切換,倍周期分岔,混沌等復雜的動力學現象.