基于屬性相關性與特征選擇的K-近鄰缺失值順序填充算法


摘要:由于K-局部近鄰插補算法無法直接計算相關性,因此在插補時難以進行特征選擇,提出一種基于屬性相關性的對于多維數據缺失按順序并進行特征選擇的填充方法,在解決相關性計算的問題同時提出了采用相關性進行填充順序選擇。算法首先提取完整數據集或者投影計算距離相關性,并按照一定的方式按相關性從大到小進行填充,保證在填充時不會因為特征選擇出現參照數據集為空的情況,在填充時選擇大于相關性臨界點的特征在投影的基礎上進行近鄰填充。實驗分別在不同缺失率下計算該方法與其它算法的均方誤差結果,結果表明,該算法在填充效果上明顯優于其它算法。
關鍵詞:距離相關性;特征選擇;順序插補
引言
數據缺失在現實中是一種非常常見的現象,它產生的原因可能是信息難以獲取或者是數據傳輸中發生錯誤產生遺漏。數據缺失會導致模型難以建立,使決策分析無法達到好的效果。數據挖掘中預處理占最大比重,而預處理中最關鍵的就是對缺失數據的處理。
常用的處理方法有加權法、刪除法和插補法。加權法通過某些方法把權數從缺失單位上轉移到非缺失單位上,刪除法則是直接刪除存在缺失單位的樣本,直接得到一個完整的數據集。刪除法雖然簡單,但當缺失率比較高的時候可能會刪除較多的樣本,產生較多誤差,因此國內外學者更希望采用其他方法來填補不完整數據,以保證數據的質量,即插補法,插補法是用一個或者多個估計值來代替缺失值的方法,前后分為單值插補和多重插補,常用的單值插補有均值填充、回歸填充、冷卡填充和熱卡填充等。
K-近鄰填充(K-nearest neighbor imputation, KNNI)是一種比較典型的冷卡填充,它是Olga Troyanskaya提出的基于局部相似性的插補算法,它將完整數據集提取出來,缺失值的近鄰樣本將從完整數據集中提取,分類值采用眾數填充,連續值采用平均數填充,這種方法的填充效果極大程度上收到了缺失率的影響,當缺失率極大時,完整數據集的樣本數量將會非常少,這意味著這種情況下得到的近鄰樣本實際上相似性并不高,這可能導致產生較大的誤差,在這個基礎上,楊日東、李琳等提出了基于局部K近鄰的填充算法,它并不直接提取完整數據集,而是在填充缺失值時,將當前樣本的完整屬性投影出來,并根據屬性投影結果從數據集中提取完整數據集,這在缺失率較大的情況下極大地改善了K近鄰插補的缺陷,但以上都并未考慮過屬性相關性以及填充順序對填充準確率的影響。劉春英提出了一種基于屬性依賴度的順序填充方法,利用填充樹按依賴度從大到小進行填充。謝霖銓、趙楠等和張曉琴、王敏都采用了主成分分析法進行二次插補。現有的將相關性應用到算法中的方法很多,但對于填充順序進行處理的方法卻相對較少,本文將通過距離相關性研究填充順序與特征選擇在提升K-近鄰填充準確率的能力。
1相關概念與原理
距離相關性(Distance Correlation)
皮爾遜相關系數常被用于度量兩個變量之間的線性相關程度,兩個變量必須服從正態分布的假設,對于非線性關系無法進行測量,即pearson相關系數為0時,兩個變量不一定是獨立的,自然界中的變量仍有大部分是非線性關系,而距離相關系數能很好地克服這個缺點,距離相關系數為0時,我們可以說這兩個變量一定是獨立的。王黎明、吳香華等對比了皮爾遜相關系數、秩相關系數、距離相關性的利弊,最終采用距離相關系數來衡量預報因子和PM2.5之間的相關性。
研究變量 和 的獨立性,記為 。當 時, 和 相互獨立; 越大,代表 和 的相關性越強。設 是總體 的隨機樣本, Székely等 (2008) 定義兩隨機變量的 和 的DC樣本估計值為
1.2K-局部投影
傳統K-近鄰填充在缺失率較大的時候可能導致完整數據集的樣本數量過小或者為空,填充時難以找到真正的近鄰,K-局部近鄰插補針對這個缺點做了改進,使能夠參考的完整數據集更多。
K-局部近鄰插補中,投影是其中最關鍵的部分。若樣本 在屬性 上的值是缺失值,對于 在數據集T上投影的完整數據子集為TC,其中 ,任意 對應的TC都是不同的。例如表1來說,如果需要對數據aB進行填充,那么缺失屬性集 ,完整數據子集 ,近鄰樣本則在TC中取舍。而對于傳統K-近鄰填充,完整數據集 。
1.3基于屬性相關性與特征選擇的K-近鄰缺失值順序填充算法
在K-局部近鄰插補中,插補從樣本中缺失值最多、屬性中缺失最少的數據開始,這說明算法的插補順序完全是由數據的缺失分布確定的,并且在計算樣本相似度時,也未曾考慮屬性之間的依賴程度,這可能導致相關性不高的屬性介入相似度計算,使計算出的近鄰是相似度不高的偽近鄰。如果要在該算法基礎上將相關性計算與它結合,有缺失值的數據集會無法進行相關性的計算,若在對每個缺失值做相似度計算前計算屬性的相關性再進行屬性篩選,這將極大地增加算法的運行時間與復雜度。因此本文將K-近鄰插補和K-局部近鄰插補兩種算法結合后進行改進,使屬性相關性能夠同時對填充順序和特征選擇作出干預,同時最小化相關性計算、順序填充和特征選擇的運算時間代價。
1.3.1 屬性相關性計算
K-近鄰插補的優點在于它直接篩選出沒有缺失值的完整數據子集,所有插補計算都在這個完整數據子集上進行,因此它十分簡便,計算速度也很快。由于不存在缺失值,距離相關性也可以在完整數據子集上很方便地計算出來。但K-近鄰插補的缺點在于,當缺失率較大時,無法找到完整數據子集或者子集容量太小無法進行計算,此時將屬性兩兩篩選完整子集進行相關性計算,最終計算出屬性相關性矩陣C。
在數據集 中,屬性集 的數量為 , 表示標簽列的數量,樣本數量為 ,樣本中存在缺失值的屬性集為 ,該數據集相關性矩陣為 。 變量 的距離相關性, ,因此 為軸對稱矩陣,其中 。當缺失率較小、通過刪除法得到的完整數據子集 的樣本數量i'占數據集T樣本數量i的比例≥一個給定的 假設值時,直接使用完整數據子集通過式(1)計算相關性矩陣 ;當缺失率較大,可能導致比率 時,通過對數據集 的屬性列 作刪除法,將得到的子集 通過式(1)計算相關性矩陣 。
1.3.2 特征選擇
在進行插補時,如果采用全部的屬性集做近鄰插補,某些屬性與待填充數據的屬性相關性較小或者是相互獨立的情況下,無論是計算相似度還是近鄰填充都會扭曲近鄰分布,降低插補的準確率,因此需要根據相關性剔除參照屬性中相關性過低的屬性。參照屬性指的是對于待插補值選出的用于計算近鄰的完整數據集的屬性,參照集是該完整數據集。對于待插補值 ,首先通過投影得到參照數據集D,其中屬性集為 ,設定相關性臨界點Cr,當 中的屬性在相關性矩陣 中的屬性 列中的對應值小于 時將剔除該屬性列。
當 時,算法不做特征處理,相當于有排序的K-局部近鄰插補; 時,表示只有強相關的屬性才能進行近鄰計算,此時將無法進行填補運算。經過大量實驗, 的取值在0.6左右表現為最好。
1.3.3 順序選擇
由于本文針對的是屬性中的缺失值插補,而標簽中的數據是完整的,因此當標簽列作為參照屬性時,不會減少參照集的樣本數量,因此當按照與標簽的相關性從大到小的順序進行插補能得到較多的參照樣本數量,在極限情況下與當前屬性的相關性只有標簽列達到臨界點要求時,不會出現參照集太小或者為空的情況。
選擇第二個填充列時,選擇 中使值最大的 作為當前填充列 ,以此類推,直到填充完畢。
1.3.4 極端情況
當數據集的缺失率較大時,存在一種情況,即選擇的填充列 與其它屬性列的相關性并不大,甚至小于 ,該列在特征選擇上會刪除所有的參照集的屬性,導致無法進行插補。對于這種情況,本文作如下設計:對于當前設定的相關性臨界點 ,如果在填充時由于 比較高導致參照集為空,那么將 減去一定的值,直到使參照集非空,然后在下一個缺失值填補時返回原設定的 值。
1.4算法的實現
基于屬性相關性與特征選擇的K-近鄰缺失值順序填充算法流程如圖1所示。
2實驗結果及分析
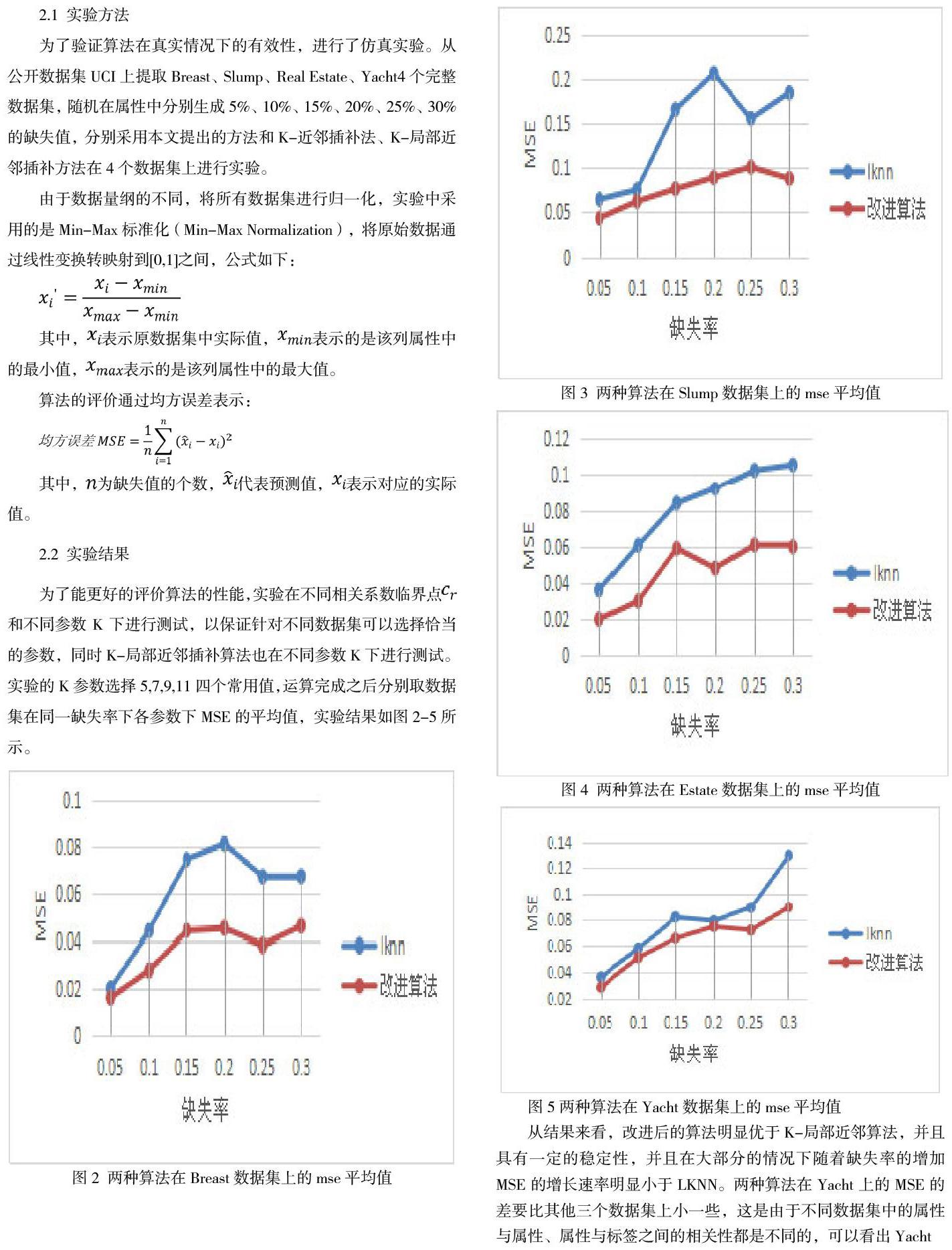
2.1 實驗方法
為了驗證算法在真實情況下的有效性,進行了仿真實驗。從公開數據集UCI上提取Breast、Slump、Real Estate、Yacht4個完整數據集,隨機在屬性中分別生成5%、10%、15%、20%、25%、30%的缺失值,分別采用本文提出的方法和K-近鄰插補法、K-局部近鄰插補方法在4個數據集上進行實驗。
由于數據量綱的不同,將所有數據集進行歸一化,實驗中采用的是Min-Max標準化(Min-Max Normalization),將原始數據通過線性變換轉映射到[0,1]之間,公式如下:
從結果來看,改進后的算法明顯優于K-局部近鄰算法,并且具有一定的穩定性,并且在大部分的情況下隨著缺失率的增加MSE的增長速率明顯小于LKNN。兩種算法在Yacht上的MSE的差要比其他三個數據集上小一些,這是由于不同數據集中的屬性與屬性、屬性與標簽之間的相關性都是不同的,可以看出Yacht數據集的相關性比較強,導致即使做了特征選擇,剔除的屬性也沒有其他三個數據集多,使算法和K-局部近鄰方法更相當一些。
3結語
為解決特征選擇無法直接在KNN局布近鄰插補法上使用的問題,本文采用K近鄰插補算法中提取完整數據集的方法計算距離相關性,并采用距離相關性同時對插補順序和特征選擇進行了融合改進,通過觀察仿真實驗結果,可知基于屬性相關性與特征選擇的K-近鄰缺失值順序填充算法在填充準確率上明顯優于K-局部近鄰插補算法。
但算法也有不足之處,在屬性值較多的情況下,頻繁進行特征選擇將大量提高算法的時間復雜度,在未來的研究中將會對這一不足之處進行優化。
參考文獻
[1]LUKASZ A K, PETR M. A survey of knowledge discovery and data mining process models[J]. Knowledge Engineering Review, 2006, 21(1):1-24.
[2]鄧建新,單路寶,賀德強,唐銳.缺失數據的處理方法及其發展趨勢[J].統計與決策,2019,35(23):28-34.
[3]王敏. 基于成分數據的缺失值補全方法研究[D].山西大學,2016.
[4]曄沙.數據缺失及其處理方法綜述[J].電子測試,2017(18):65-67+60.
[5] TROYANSKAYA O, CANTOR M, SHERLOCK G, et al. Missing value estimation methods for DNA microarrays. Bioinformatics, 2001, 17(6): 520-525.
[6]楊日東,李琳,陳秋源,周毅.LKNNI:一種局部K近鄰插補算法[J].中國衛生統計,2019,36(05):780-783.
[7]劉春英.基于屬性依賴度的缺失值順序填充算法[J].計算機應用與軟件,2013,30(09):215-218.
[8]謝霖銓,趙楠,徐浩,畢永朋.基于屬性相關性的K N N近鄰填補算法改進[J].江西理工大學學報,2019,40(01):95-101.
[9]張曉琴,王敏.基于主成分分析的成分數據缺失值插補法[J].應用概率統計,2016,32(01):101-110.
[10]王黎明,吳香華,趙天良,程國勝,張祥志,湯莉莉,賈夢唯,陳煜升.基于距離相關系數和支持向量機回歸的PM_(2.5)濃度滾動統計預報方案[J].環境科學學報,2017,37(04):1268-1276.
作者簡介:唐晗,女,1993年11月,漢,江西省吉安市,工學學士,江西應用工程職業學院,數據挖掘。

