高軌衛星的月球引力攝動效應研究

趙東方，張捍衛

（1. 河南理工大學 測繪與國土信息學院，河南 焦作 454003；2. 河南理工大學 資源與環境學院，河南 焦作 454003）

0 引言

近年來，隨著我國北斗衛星導航系統（BeiDou navigation satellite system, BDS）的逐步建立，BDS越來越多地應用到測繪、導航制導、氣象等領域[1]。而各項應用對定位的要求越來越高，使得對衛星定軌的要求也越來越高。而衛星在圍繞地球運行過程中，受到的主要攝動包括地球非球形引力攝動、第三體引力攝動、輻射壓力攝動、潮汐攝動、大氣阻力攝動等[2]。各種攝動因素對不同軌道的影響是不同的。

除去地球和空間探測器外，第三個天體引力對空間探測器產生的攝動，稱為第三體引力攝動。而對于圍繞地球的衛星而言，第三體引力攝動主要是由日月引力產生的，稱為日月引力攝動。繞地運行衛星軌道高度越高，第三體引力攝動的影響就越大。對于高軌繞地運行的衛星，第三體引力攝動的影響十分可觀。第三體引力攝動對高軌衛星的影響將僅次于地球中心引力和地球非球形引力攝動[3]。

文獻[4]指出對于圍繞地球運行的衛星而言，第三體引力攝動影響的大小，主要取決于衛星軌道的高度、形狀、軌道面位置和拱線相對于月地、日地連線的位置。文獻[5]指出，第三體引力攝動對偏心率和傾角有影響，而地球扁率項J2對其沒有影響。

因此，對第三體引力攝動的研究，可以探究第三體引力攝動對繞地運行衛星軌道的影響規律和大小，對于衛星軌道保持、自主定軌等都有積極的意義。

由于第三體引力攝動對于高軌衛星的影響更為顯著，而BDS 中有多顆地球靜止軌道（geostationary Earth orbit, GEO）衛星和傾斜地球同步軌道（inclined geosynchronous orbits, IGSO）衛星的高度都在35 000 km 左右[6]，屬于高軌衛星，受到第三體引力的影響較大。因此，對第三體引力攝動的研究，也對BDS 也有積極的意義。

本文主要研究的是在不同衛星軌道面與地月連線向量夾角下，月球引力攝動對高軌衛星的影響。

1 基本原理

衛星運動的微分方程都很復雜，除最簡單的二體等少數問題外，到目前為止都不能給出嚴格解。而衛星的實際運動受到各種攝動因素的影響，其實際微分方程十分復雜，很難給出準確的解析解。而運用數值解法，可以給出滿足一定精度的離散解，可以定性與定量地分析衛星運動的各種規律[7]。

文獻[8]指出，利用龍格-庫特塔-費爾布爾格（Runge-Kutta-Fehlbrg, RKF）單步法，先求出12 步解，然后采用12 階亞當斯（Adams）預估-校正公式往后積分，步長采用75 s，每隔15 min輸出一組結果。結果表明，二體意義下對地球靜止軌道衛星和傾斜地球同步軌道衛星的數值積分結果與真值相差甚小，均在亞毫米級或以內。文獻[9]采用2005-06-07（年積日第158 天）的全球定位系統（global positioning system, GPS）PRN1 衛星星歷，利用Adams 數值積分對PRN1衛星的運動方程進行求解。PRN1 衛星星歷由國際全球衛星導航系統（global navigation satellite system, GNSS）服務組織（International GNSS Service, IGS）提供。積分初值采用IGS 網站下載的G 文件中，年積日第158 天12 時的數據作為初值，積分步長采用75 s，每隔15 min 輸出一組結果，積分時間為20 h，將結果與IGS 精密星歷比較。結果顯示，該數值積分結果與精密星歷差值在2 cm 左右。說明Adams 數值積分方法對于確定衛星軌道是可靠的。

1.1 RKF7、RKF8 單步積分法

RKF 方法是一種嵌套技術的龍格-庫特塔（Runge-Kutta, RK）方法，利用差分格式中右函數系數可有不同選擇的特點，即同時給出n階和n+1階兩組RK 計算公式，用兩組公式計算結果之差來估計截斷誤差，根據截斷誤差的大小來控制步長。本文采用的是RKF7、RKF8 來進行起步，RKF 的7 階（RKF7）和8 階（RKF8）公式[10]為

式中：T為截斷誤差；f10、f11、f12分別為式（2）中k=10、k=11、k=12 時fk的值。

1.2 Adams 預估校正法

在衛星運動方程的數值解法中，單步法的優點是起步和變步長比較容易，但是計算量較大。所以單步法通常用作多步法計算的起算數據。當采用單步法計算出足夠的起算數據后，就可采用效率更高的多步法進行積分[11]。本文使用的是12 階Admas 預估-校正法，預估用顯式的亞當斯-巴什福斯（Admas-Bashforth）公式為

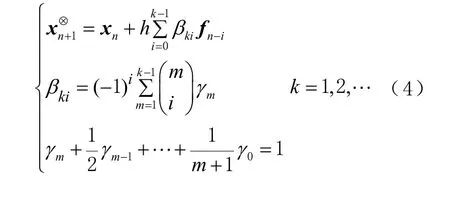
校正用隱式的亞當斯-莫爾頓（Adams-Moulton）公式為

1.3 滑動拉格朗日插值法

利用式（7）在X、Y、Z方向上分別進行插值處理，即可得到任意時刻的衛星坐標。為了提高插值精度，常利用高階拉格朗日插值多項式，但是這又會出現插值區間兩端不穩定，易發生震蕩或跳躍現象，這種情況被稱為“龍格”現象。

為了解決“龍格”現象，可以采用滑動拉格朗日插值法解決插值區間兩端不穩定的問題。該方法使待內插點始終處于插值區間的中央，將插值區間作為一個固定“窗口”，該“窗口”長度固定。“窗口”每向后移動一個單位，內插點也隨之向后移動一個單位[13]。本文采用8 階滑動拉格朗日插值。文獻[14]指出利用8 階滑動式拉格朗日插方法對衛星插值可以達到毫米級。

2 數值計算

2.1 處理流程

衛星初始狀態經過RKF7、RKF8 單步法積分，求得足夠的多步法積分的起步數據；再由Adams預估-校正法求得衛星在一定時間內，一定時間間隔的衛星位置矢量和衛星速度矢量，轉化為衛星軌道根數；最后用8 階滑動拉格朗日插值法求得衛星加速度。

2.2 數據準備

在利用數值積分進行衛星軌道積分過程中，除了考慮月球引力外，還需考慮的力學模型包括表1中所示的力學模型。表2 是一組衛星初始時刻的軌道參數，其中a為衛星軌道的長半軸，e為衛星軌道的偏心率，M為衛星軌道的平近點角，ω為衛星軌道的近地點幅角，Ω為衛星軌道的升交點赤經，i為衛星軌道的傾角，α為地月連線向量與衛星軌道面的夾角，夾角α范圍為 0 ≤α≤ 180° 。

使用表1 中的力學模型，分別對表2 中各個衛星進行軌道數值積分，衛星質量都為1 500 kg，積分時間長度為48 h，歷元間隔為75 s，輸出數據的間隔為15 min。

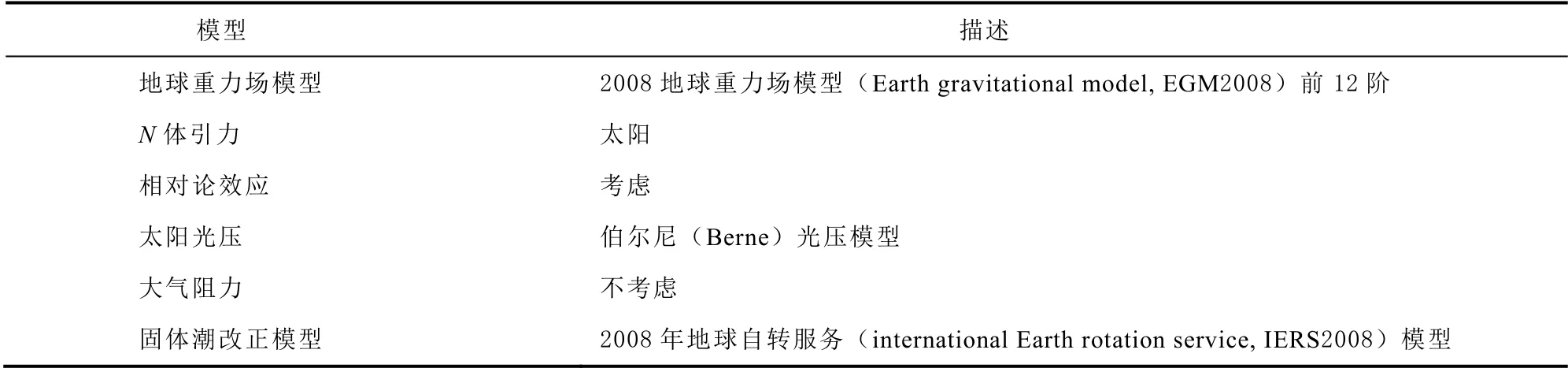
表1 力學模型

表2 衛星初始時刻軌道根數

3 結果分析

通過計算，得到了月球引力攝動加速度和兩個周期軌道根數隨夾角α和時間的變化情況，如圖1至圖12 所示。兩個周期時間可根據開普勒第三定律計算。

開普勒第三定律為

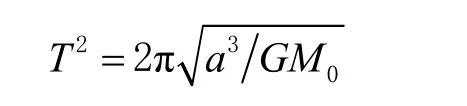
式中：T為衛星運行周期；a為衛星軌道的長半軸，G為引力常數，M0為地球質量。

根據開普勒第三定律可以計算出，在不同夾角α下，衛星的2 個周期時間大約為2 874 min。

3.1 衛星月球引力攝動加速度的變化規律

圖1 為衛星月球引力攝動加速度隨夾角α變化的情況，圖2 為衛星月球引力攝動加速度隨時間變化的情況。從圖2 中可以看出，月球引力攝動加速度的大小為3.0×10-6～8.4×10-6m/s2；當α從0 和180°趨向90°時，月球引力攝動加速度逐漸減小。在夾角α一定的情況下，月球引力攝動加速度隨時間呈一定的周期性變化，震動幅度隨著夾角α趨向90°而減小。

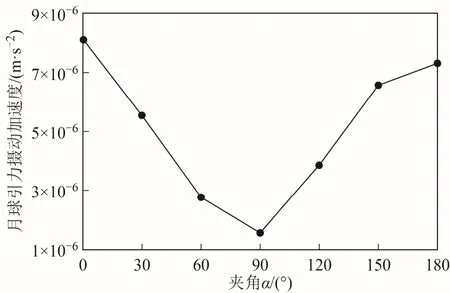
圖1 月球引力攝動加速度隨夾角α 變化情況

圖2 月球引力攝動加速度隨時間變化情況

3.2 衛星軌道長半軸變化規律

圖 3 為兩個周期長半軸增量隨夾角α變化的情況，圖4 為長半軸改變量隨時間變化的情況。從圖3、圖4 可以看出，月球引力使得長半軸長度減小；兩個周期長半軸長度增量絕對值最大位于α=180°處，為0.59 km；長半軸長度增量絕對值最小位于α=90°處，為0.23 km；長半軸增量絕對值隨著夾角α趨向90°而減小。長半軸改變量隨時間呈現周期性變化，震動幅度隨著夾角α趨向90°而減小。

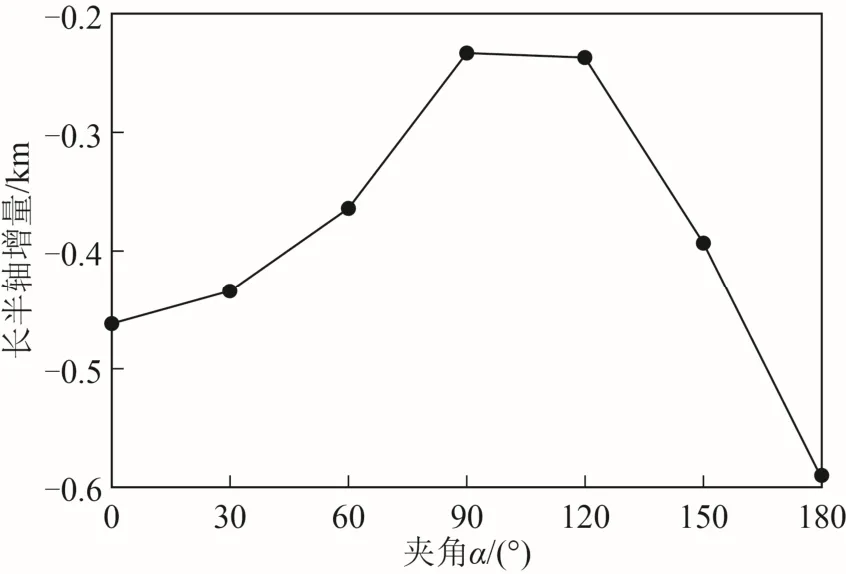
圖3 軌道長半軸兩個周期增量隨夾角α 變化情況

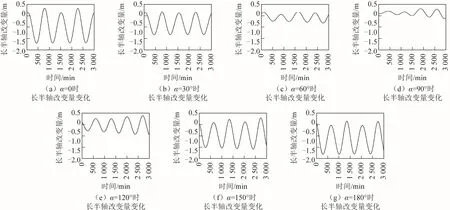
圖4 月球引力引起長半軸改變量隨時間變化情況

3.3 衛星軌道偏心率變化規律

圖5 為兩個周期衛星軌道偏心率增量隨夾角α變化的情況，圖6 為偏心率改變量隨時間變化的情況。從圖5、圖6 可以看出，當0≤α＜90°時，兩個周期偏心率增量逐漸變大；當90°＜α≤180°時，兩個周期偏心率增量逐漸變小。偏心率改變量隨時間震蕩變化，震蕩幅度在α=0 和α=180°附近最大，隨著α趨向90°震蕩幅度逐漸減小。

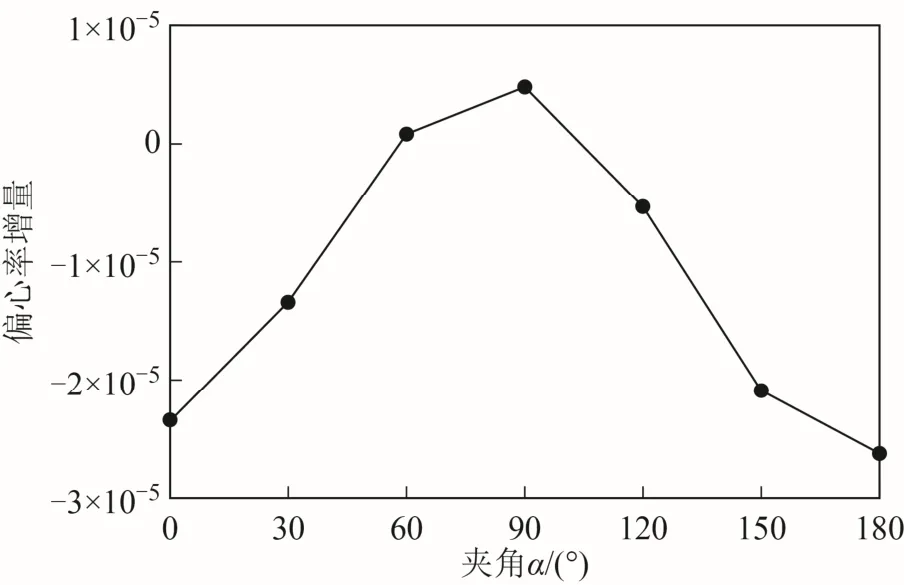
圖5 軌道偏心率兩個周期增量隨夾角α 變化情況

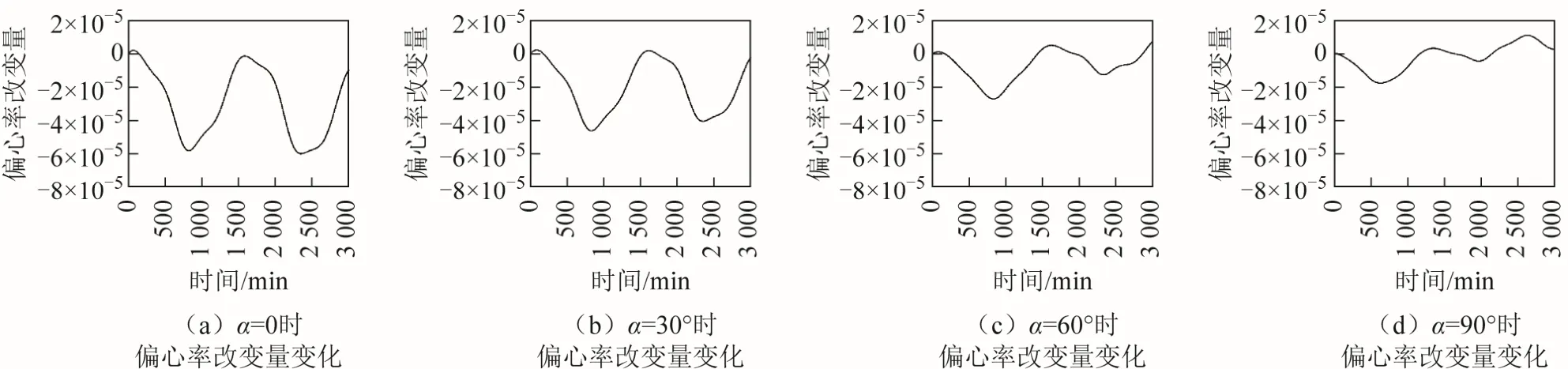
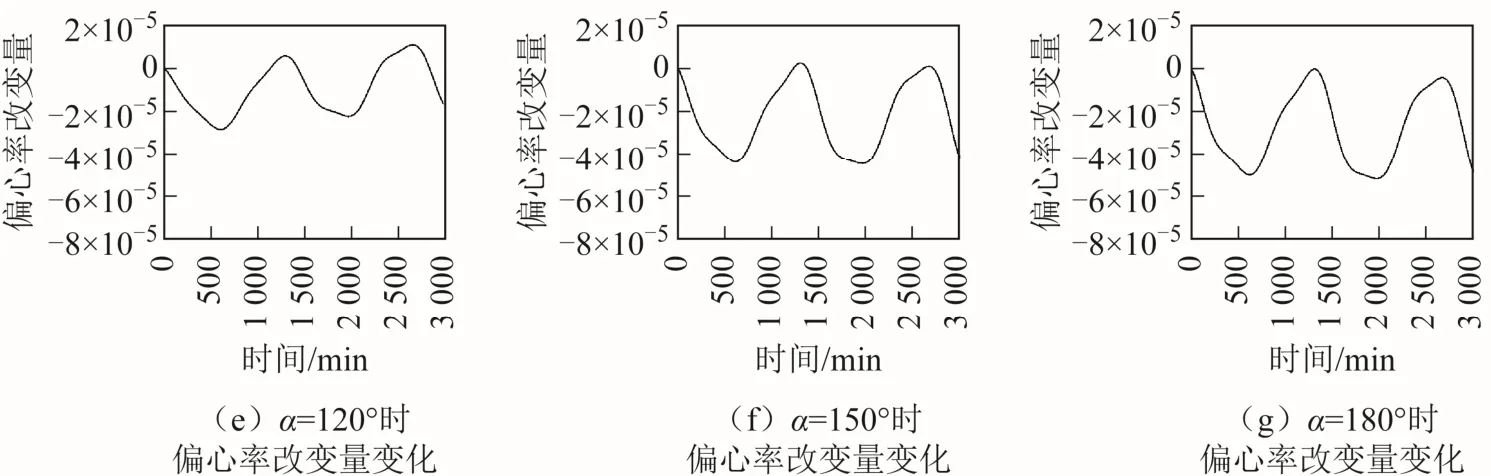
圖6 月球引力引起偏心率改變量隨時間變化情況

3.4 衛星軌道平近點角變化規律

圖7 為兩個周期平近點角增量隨夾角α變化的情況，圖8 為平近點角改變量隨時間變化的情況。從圖7、圖8 可以看出，兩個周期平近點角增量先增加后減小，再增加；增量絕對值在α=0處取得最大值為0.046°。平近點角改變量隨時間呈一定的周期性波動，震蕩幅度在α=0 和α=180°附近最大，隨著夾角α趨向90°震蕩幅度逐漸減小。

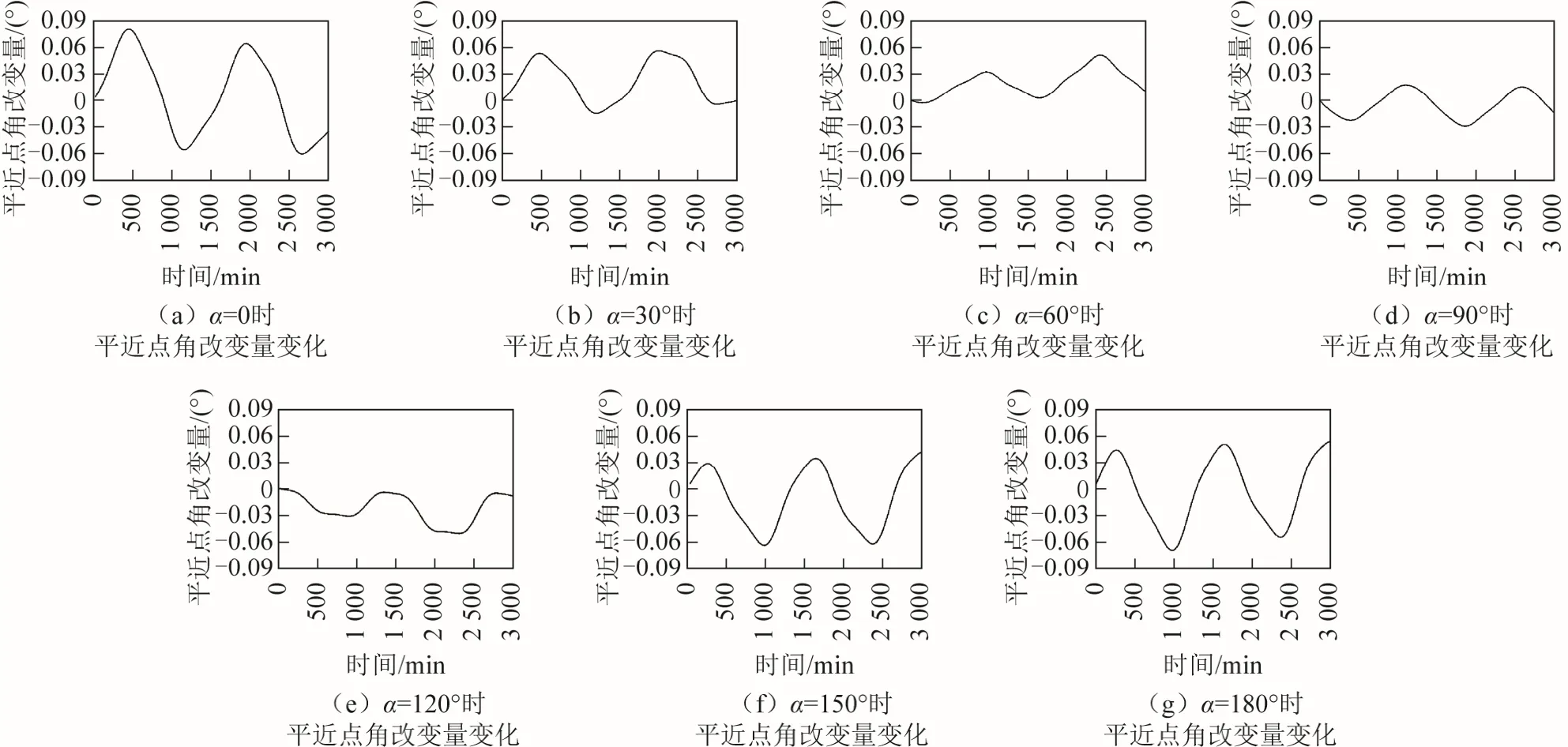
圖8 月球引力引起平近點角改變量隨時間變化情況

3.5 衛星軌道升交點赤經變化規律

圖9 為兩個周期升交點赤經增量隨夾角α變化的情況，圖10 為升交點赤經改變量隨時間變化的情況。從圖9、圖10 可以看出，當α=120°時，升交點赤經增量絕對值最大為 0.000 25°。當0≤α＜90°時，升交點赤經改變量隨時間減小；當 90°＜α≤180°時，升交點赤經改變量隨時間增加。

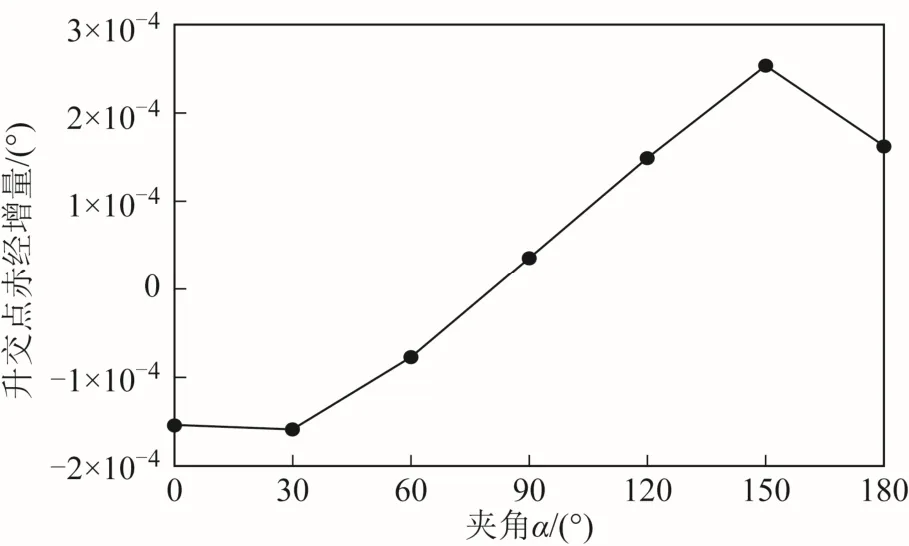
圖9 軌道升交點赤經兩個周期增量隨夾角α 變化情況

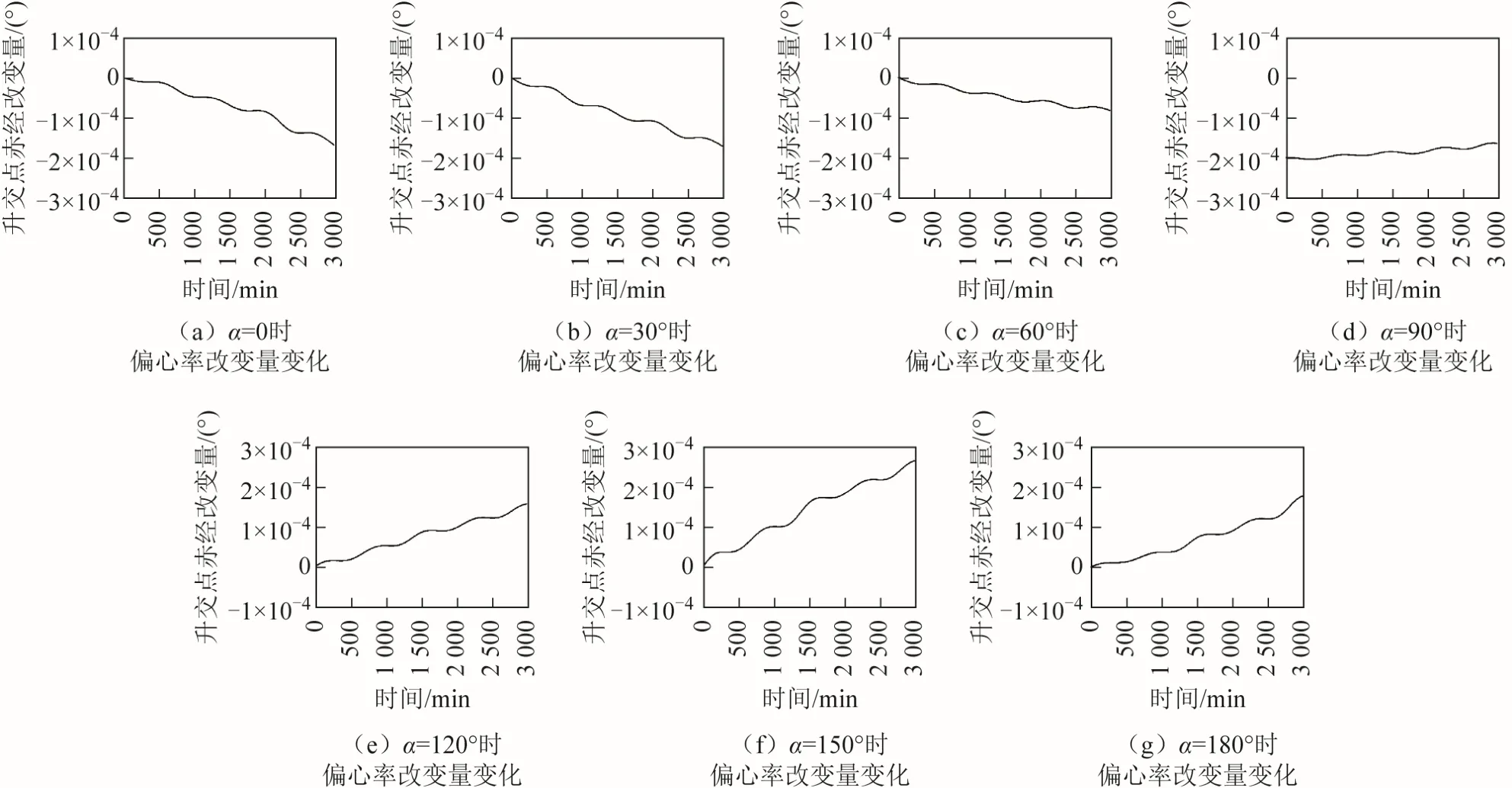
圖10 月球引力引起升交點赤經改變量隨時間變化情況

3.6 衛星軌道傾角變化規律

圖11 為兩個周期軌道傾角增量隨夾角α變化的情況，圖12 為軌道傾角改變量隨時間變化的情況。從圖11、圖12 可以看出，當α趨向90°時，兩個周期軌道傾角增量逐漸變大；在夾角α=90°時，兩個周期軌道傾角增量絕對值最大為0.000 09°；當夾角α=0 或α=180°時，兩個周期軌道傾角增量絕對值最小為0.000 014°。軌道傾角改變量隨時間都逐漸增加。

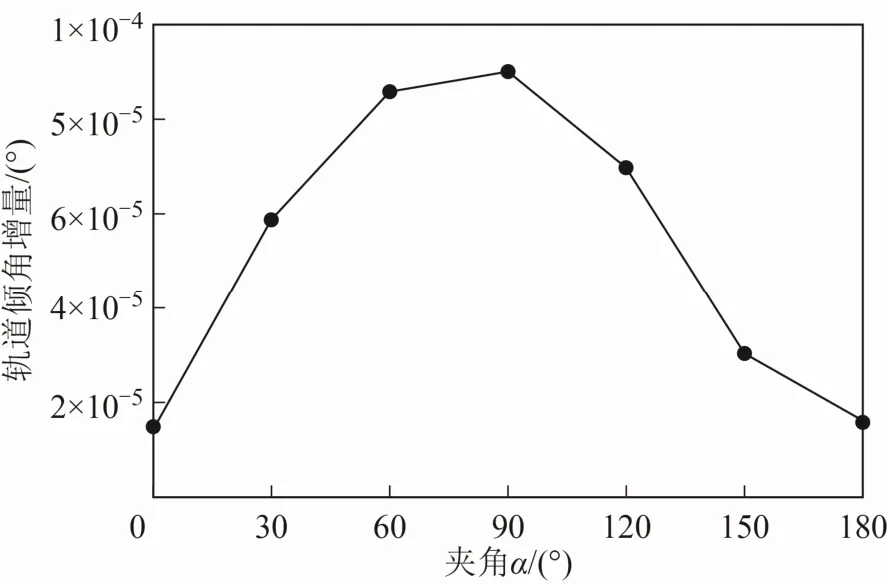
圖11 軌道傾角兩個周期增量隨夾角α 變化情況

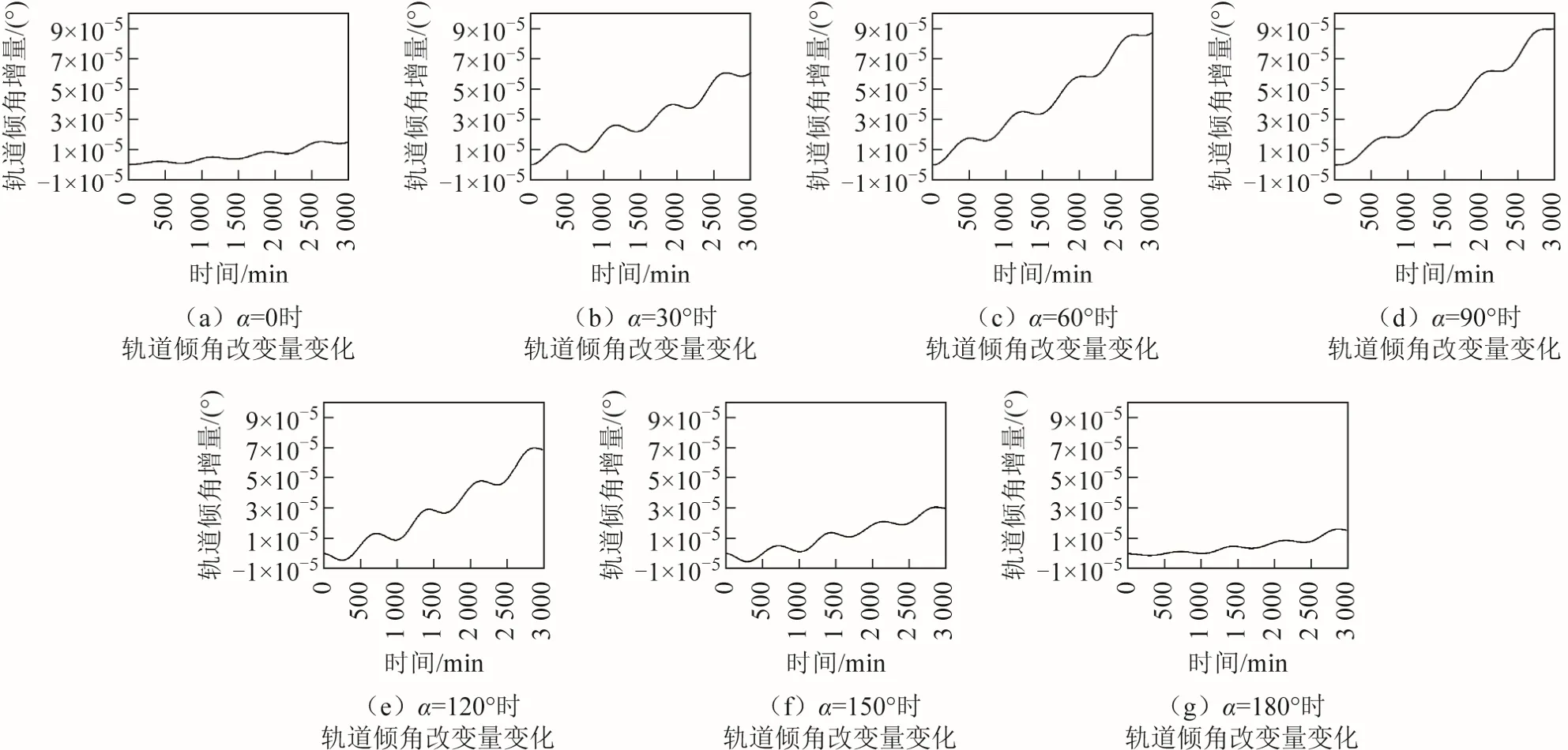
圖12 月球引力引起傾角改變量隨時間變化情況

4 結束語

本文以軌道長半軸為42 167.26 km 的一組衛星為研究對象，通過數值方法對其進行積分。計算結果表明，經過兩個周期，當衛星軌道面與地月連線共面時，月球引力對加速度、軌道長半軸、軌道偏心率和軌道平近點角的影響最大；當衛星軌道面與地月連線垂直時，月球引力對軌道傾角的影響最大。其中，月球引力對衛星軌道的長半軸和平近點角影響較大，分別可達0.59 km 和0.046°。這將有助于認識和了解短時期月球引力對高軌航天器造成的影響。