濟南地區加權平均溫度模型建立及精度分析

徐銘澤，郭秋英，侯建輝，趙 耀，孫英君，李德偉

（1. 山東建筑大學 測繪地理信息學院，濟南 250101；2. 中國測繪科學研究院 北京房山人衛激光國家野外科學觀測研究站, 北京 100036）

0 引言

水汽是大氣重要組成部分，對流層底部分布的水汽約為大氣水汽總含量的99%，是大氣中較為活躍，同時也是難以描述的參數之一[1-2]。水汽作為溫室氣體作用顯著，能夠影響輻射平衡，是云和降水形成的催化劑，也是短期降水預報的關鍵因子。掌握大氣中水汽的分布，對于天氣及洪澇災害預報具有十分重要的意義[3-4]。

無線電探空儀（radiosondes，RS）能夠獲取垂向分辨率極高的大氣可降水量（precipitable water vapor，PWV）數值，但因探空氣球成本高昂，每天只能在00:00 及12:00 收集數據，全球探空站數量分布少，導致其時空分辨率較低。微波輻射計的時間分辨率可達5～8 min，但在雨雪天氣或有云層遮擋時，會產生明顯的觀測偏差，無法滿足全天候的觀測精度要求[5]。全球衛星導航系統（global navigation satellite system，GNSS）技術因其高精度、全天候、高時空分辨率的優點，成為探測大氣水汽的重要補充，廣泛應用于氣象學領域[6]。其原理為通過解算衛星信號穿過對流層時受到大氣的折射而產生信號時延可獲得精確的天頂對流層延遲（zenith total delay, ZTD）。天頂靜力學延遲（zenith hydrostatic delay, ZHD）可通過薩斯塔莫伊寧（Saastamoinen）模型精確計算[7]，天頂對流層延遲減去天頂靜力學延遲即可得到天頂濕延遲（zenith wet delay, ZWD），由ZWD 計算PWV 時需要無量綱轉換系數∏，二者共同影響PWV 的精度。轉換系數∏是關于加權平均溫度（atmospheric weighted mean temperature, Tm）的函數，即Tm的準確與否關系到∏的精度。為獲取與研究地區相符合的大氣加權平均溫度模型，眾多學者進行了多項研究。文獻[8]利用貴州地區的無線探空站的觀測數據，建立了貴州整體及局部的加權平均溫度Tm與地面溫度Ts間的一元線性關系式。文獻[9]利用香港地區的探空數據，建立符合香港地區的加權平均溫度與地面溫度單因子和加權平均溫度與地面溫度、濕度、水汽壓的多因子加權平均溫度模型。文獻[10]則針對季節更替，提出了顧及季節變化的加權平均溫度模型，增加季節變化參數后的模型精度有所提高。文獻[11]利用2005—2011 年全球大地測量觀測系統（global geodetic observing system, GGOS）提供的Tm數據及歐洲中期天氣預報中心（European Center for Medium-range Weather Forecasts, ECMWF）提供的Ts數據，得出緯度影響二者的相關性的結論，按緯度建立起全球分區域線性回歸模型。文獻[12]同樣利用GGOS Tm數據以及ECMWF Ts的再分析資料數據，建立顧及季節性適合澳洲地區的加權平均溫度模型，該模型精度高于再分析資料數據且更符合探空積分計算值。文獻[13]則針對遠海等缺乏探空資料的區域，利用近海探空資料及ECMWF 提供的ERA-Interim再分析資料構建適用于遠洋地區的、平均轉換誤差僅為1%的回歸模型。此外，文獻[14-16]也分別建立銀川地區加權平均溫度模型、吉林地區非線性加權平均溫度模型以及香港地區添加高度改正的區域模型。

基于以上研究，本文利用濟南地區章丘探空站（站號54727）2015—2019 年共5 年探空資料數據，建立符合濟南地區的大氣加權平均溫度模型與貝維斯（Bevis）模型、中國東部地區模型進行精度對比與分析，并利用濟南加權平均溫度模型進行PWV 反演實驗，分析濟南地區PWV 與實際降水的關系，為濟南地區氣象探測等方面的應用提供參考依據。

1 加權平均溫度 Tm計算

在GNSS 氣象學中，ZWD 與PWV 間的轉換因子∏的計算公式為

式中：e為水汽壓，單位為hPa；T為絕對溫度，單位為K；h為大氣厚度，單位為m。

目前，Tm的計算方法有多種，包括常數法、經驗公式法等，但目前精度最高的方法是利用探空資料、采用數值積分法解得Tm，其計算公式為

式中：iT為第i層大氣的平均溫度，單位為K；ihΔ 為第i層大氣的平均厚度值，單位為m；ie為第i層大氣的平均水汽壓，單位為hPa。ie的計算方法為

式中：r為相對濕度；es為飽和水汽壓，單位為hPa；t為露點溫度，單位為℃。當t＜0℃時，使用式（5）進行計算，否則使用式（6）計算[18]。

文獻[2]首次通過收集北美地區（緯度為27°N～65°N），總計8 718 次探空數據，建立起適用于中緯度、均方根誤差為4.74 K 的一元線性Bevis經驗公式，即

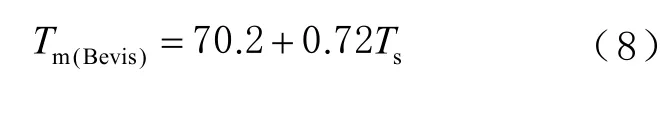
文獻[3]利用1992 年的探空資料，回歸分析出適合中國東部地區（緯度為20°N～50°N，經度為100°E～130°E）的各個月份加權平均溫度與地面溫度（Tm/Ts）線性關系式，全年平均參量化方程為

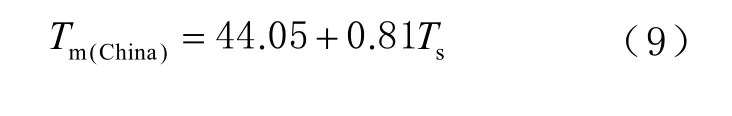
2 濟南區域加權平均溫度區域模型構建

濟南地區并無相關加權平均溫度模型，為了在該地區更好地進行GNSS 水汽反演實驗，運用上述數值分析的方法結合探空數據，建立濟南區域加權平均溫度模型。

2.1 數據預處理

數據來源為美國懷俄明大學（The University of Wyoming，UW）提供的濟南市章丘探空站2015—2019 年共5 年的觀測數據，探空站的平面位置為（36.70° N，117.55° E），高程為123.0 m。使用數值積分法計算探空站每日00:00、12:00 的Tm值，取平均值輸出作為該日的Tm最終參考值。地面溫度Ts數據由 ECMWF ERA-5 再分析資料、地面2 m 溫度每日00:00、12:00 的數據取平均值獲得。因為在釋放氣球時，可能會遇到數據無法收集或遺失的現象，由此造成某時間段的數據缺失，本次實驗采集到2015—2019 年共3 606 個數據樣本。

2.2 Tm/Ts線性回歸分析

將上述收集到的探空數據進行預處理，剔除缺失或無法使用的數據。借助矩陣實驗室（matrix laboratory, MATLAB）應用軟件編寫程序代碼，讀取經預處理后的數據。通過數值積分法，計算樣本的每日加權平均溫度值Tm，圖1 為Tm/Ts隨時間變化關系趨勢圖。

從圖1 可以看出，冬季的Tm/Ts差值小，夏季的Tm/Ts差值大，這可能與冬季較為干燥，夏季多雨水有關。無論是Tm還是Ts值，變化趨勢均滿足以年為單位的周期循環，在每年的1—7 月份上升，7 月份達到峰值后逐月遞減，二者的變化幅度也基本相同。Tm的峰值穩定在292～295 K 附近，Ts的峰值則位于300 K 上下，Tm/Ts在2015—2019 年間的變化情況基本穩定，并且Tm值低于Ts值。根據二者的變化趨勢可知，Tm/Ts之間存在良好的線性相關關系。利用最小二乘原理采用線性回歸方法，擬合Tm/Ts散點分布圖及趨勢線，其結果如圖2 所示。

圖1 章丘站Tm/Ts時間變化趨勢

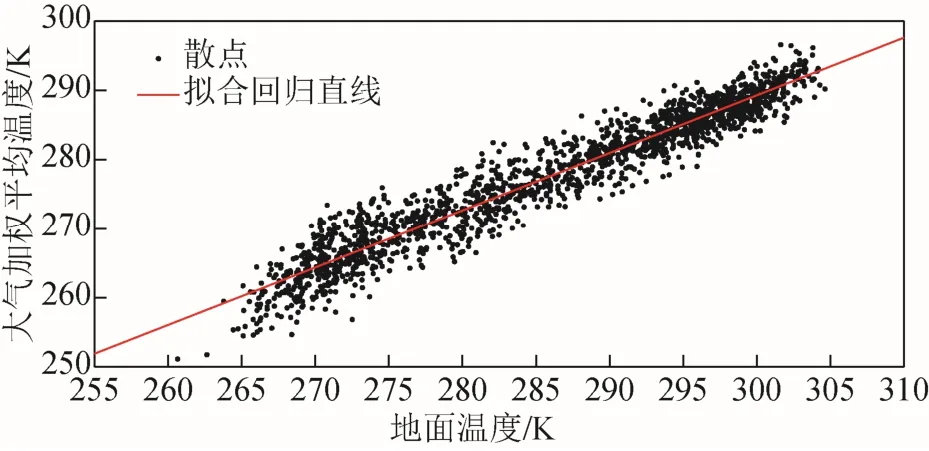
圖2 章丘站Tm/Ts散點圖及趨勢線

由圖2 散點的分布可以看到，所有的散點均集中分布于回歸趨勢線附近，二者的相關系數R為0.927 1，具有極好的線性集中關系，這也說明二者有很好的線性相關關系。

2.3 濟南地區大氣加權平均溫度模型

為了更清晰地表示加權平均溫度與地面溫度全年變化情況，圖3 給出了2015—2019 年間Tm/Ts逐月散點關系圖。

由圖3 可知，各個月份的散點均大致分布于回歸線上下，其中2015—2019 年間，Tm/Ts相關性最高的月份為4 月份，相關系數為0.798 1；相關性最低的月份為6 月份，相關系數為0.545 3，全年12 個月份的相關系數均大于0.5，各個月份的Tm/Ts值均存在線性相關關系。

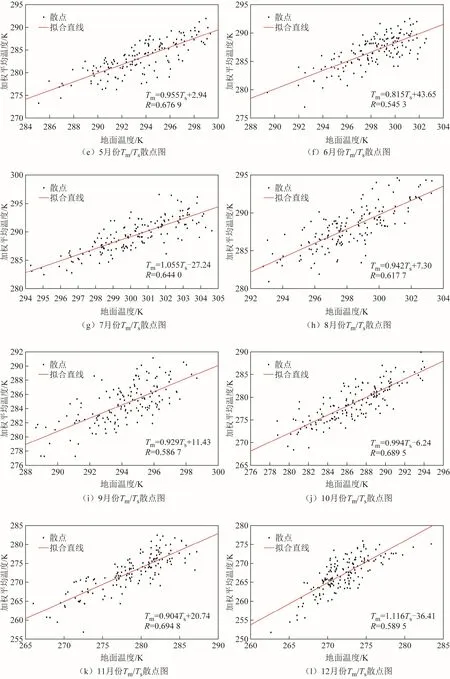
圖3 2015—2019 年章丘探空站Tm/Ts逐月散點圖

表1 為章丘探空站Tm/Ts的相關參數統計值表。

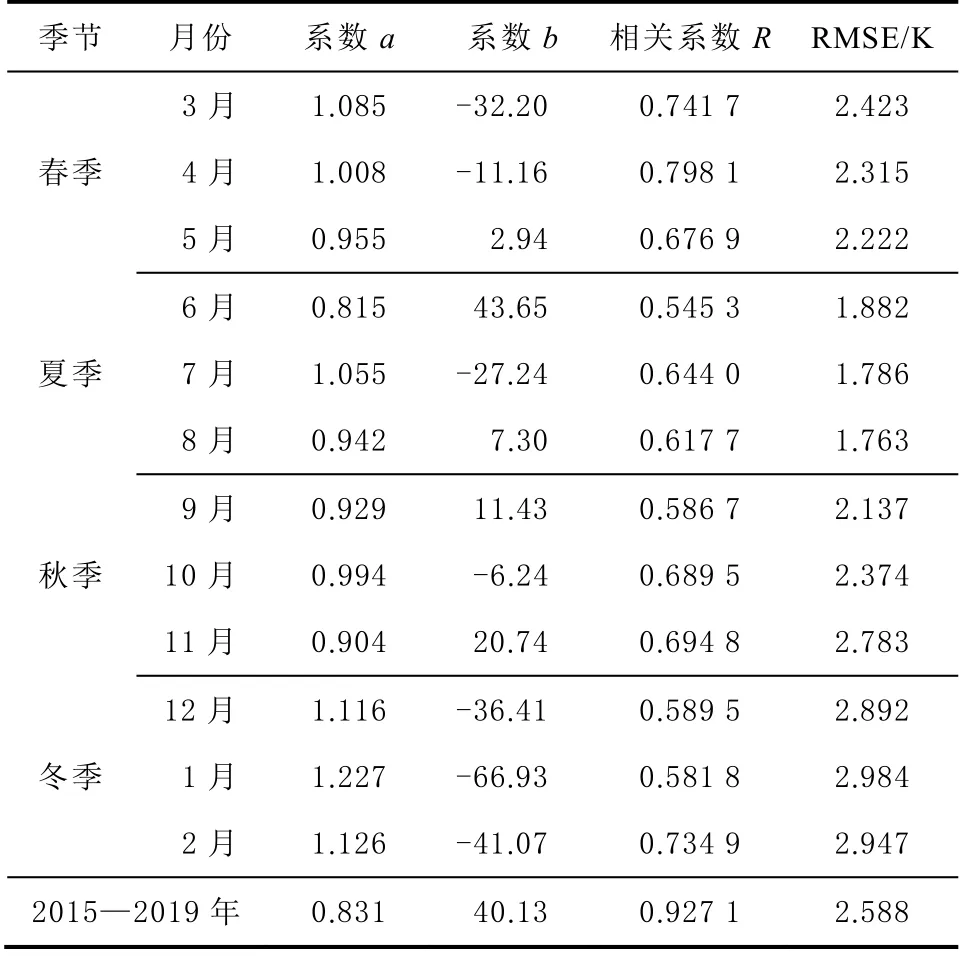
表1 2015—2019 年章丘探空站Tm/Ts逐月相關參數

由表1 可知，各月份間的均方根誤差（root mean square error，RMSE）差距較大。冬季各月份的均方根誤差分別為2.892、2.984、2.947 K，均大于全年的均方根誤差2.588 K；夏季各月份的均方根誤差值分別為1.882、1.786、1.763 K，均小于全年的均方根誤差。冬季與夏季的均方根誤差的平均值分別為2.941、1.810 K，相差1.131 K。因此，在進行反演大氣可降水量時，應選擇相應月份的模型進行反演實驗。根據2015—2019 年章丘探空站的探空數據，本文建立的濟南大氣加權平均溫度模型為

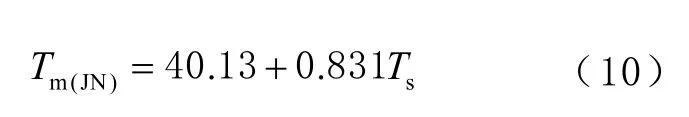
3 濟南加權平均溫度模型精度驗證與應用分析

3.1 濟南加權平均溫度模型精度驗證

3.1.1 內符合精度驗證與分析

為了驗證本文建立的濟南地區大氣加權平均溫度模型的內符合精度[19]，利用章丘探空站2015—2019 年的探空資料進行模型精度對比分析。將利用探空數據解算的Tm每日平均值作為參考值，由濟南加權平均溫度模型計算的Tm值為擬合值。圖4 為探空資料Tm參考值與模型擬合值之間的模型殘差分布情況。

從圖4 統計結果知，濟南加權平均溫度模型的殘差滿足正態分布，其中-3～3 K 區間的殘差所占比重為75.14%，93.3%的殘差位于±5 K 區間內。由此初步可以看出，本文建立的濟南加權平均溫度模型擬合程度很高。

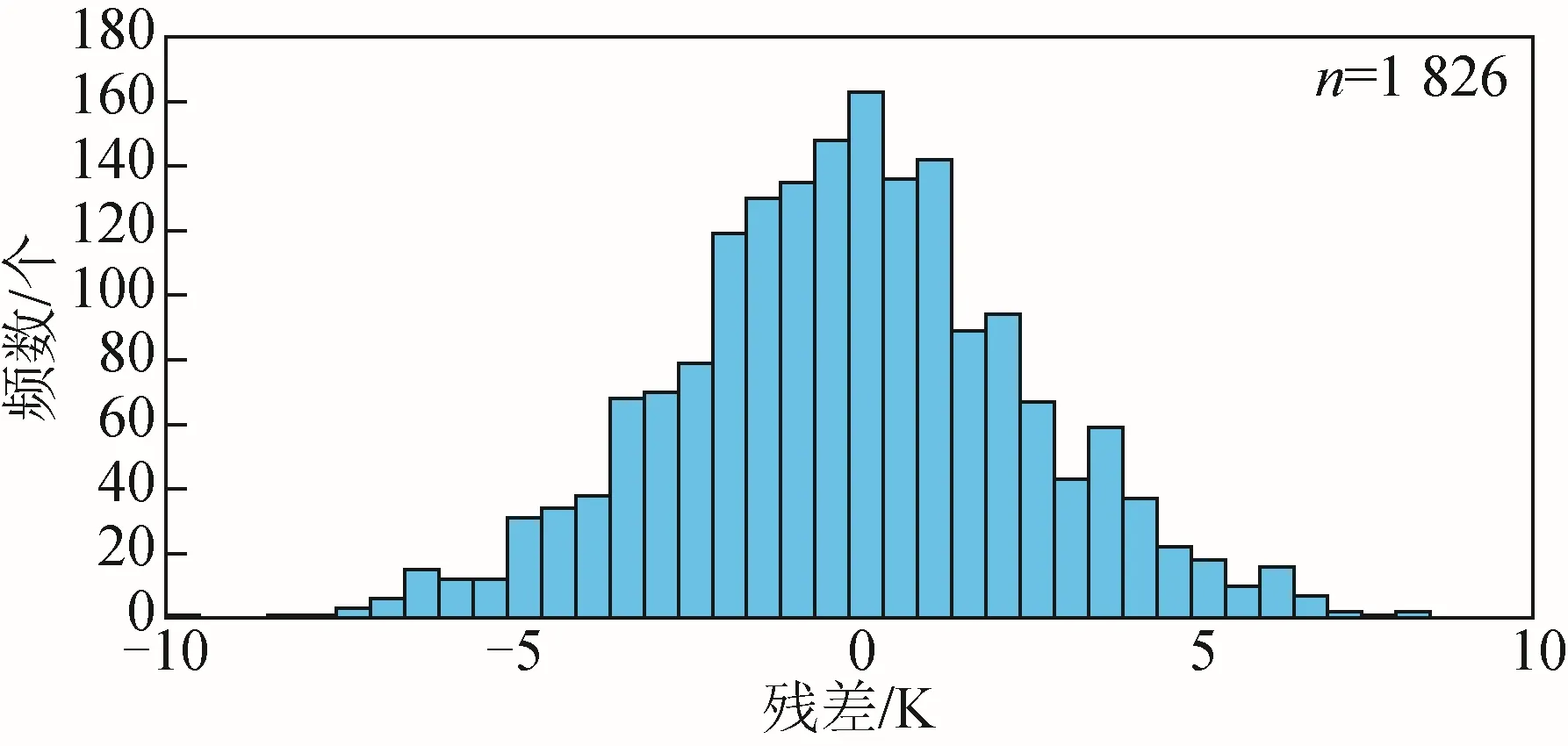
圖4 濟南加權平均溫度模型殘差分布直方圖

為了進一步分析濟南加權平均溫度模型在濟南地區的精度，將濟南加權平均溫度模型（Tm(JN)模型）與Bevis 模型（Tm(Bevis)模型）、中國東部地區模型（Tm(China)模型）進行精度對比分析，計算三種模型在濟南地區2015—2019 年的均方根誤差RMSE、平均絕對誤差（mean absolute error，MAE）和偏差（Bias），結果如表2 所示。

表2 Tm(JN)模型與Tm(Bevis)模型、Tm(China)模型精度對比 單位：K

由表2 可知，Tm(Bevis)模型與Tm(China)模型的均方根誤差、平均絕對誤差、偏差數值相近，兩種模型的精度大致相同；Tm(JN)模型的均方根誤差、平均絕對誤差、偏差分別為2.586 7、2.205 0、-0.010 9 K 均低于另外兩種模型，精度大為提高。其中，Tm(JN)模型的偏差值較Tm(Bevis)模型及Tm(China)模型分別減小了1.5 K 及1.9 K，均方根誤差較Tm(Bevis)模型及Tm(China)模型精度分別提高20%和21%，平均絕對誤差精度則分別提高25%和23%。說明本文建立的濟南加權平均溫度模型較已有模型精度更高，可靠性更好。

從表2 可以進一步看出，中國東部地區模型在濟南地區的精度要低于濟南加權平均溫度模型。為了提高中國東部地區模型在濟南地區的精度和適用性，現利用章丘探空站數據對中國東部地區模型進行優化。由探空數據解算的Tm與中國東部地區模型計算的Tm(China)之間的相關系數R為0.927，二者具有極好的線性相關關系。根據Tm與Tm(China)間的相關關系，利用最小二乘線性回歸方法對中國東部地區模型進行優化，構建適用濟南地區的中國東部地區優化模型式為

由表3 可知，適用于濟南地區的中國東部地區優化模型的精度有了大幅提高，優化后的中國東部地區模型偏差值變化極小，均方根誤差精度提高17.8%，平均絕對誤差精度提高25.5%。經優化后的中國東部地區模型精度與濟南加權平均溫度模型精度大致相當，提高了該模型在濟南地區的適用性。

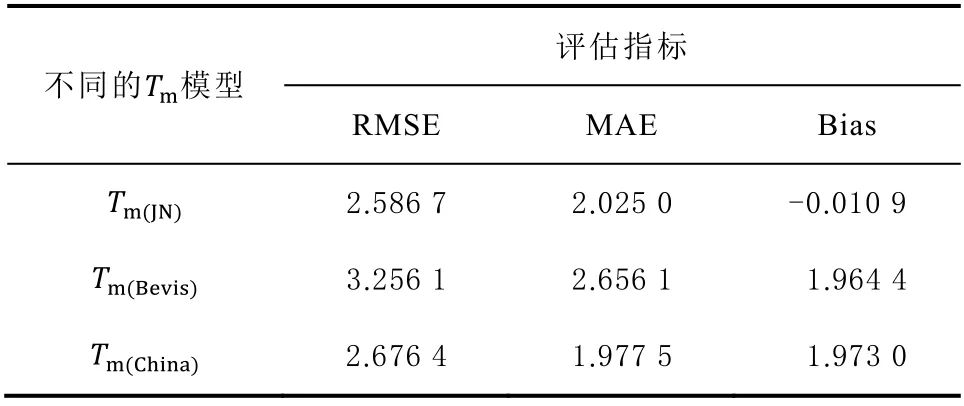
表3 中國東部地區模型優化精度對比分析 單位：K

3.1.2 外符合精度驗證與分析

為了檢驗濟南加權平均溫度模型在其他年份是否適用，檢驗分析其外符合精度，采用章丘探空站2020 年1 月1—18 日探空資料的Tm值為參考值，Tm(JN)模型計算值為預報值，同時與Tm(Bevis)模型、Tm(China)模型的預報值進行對比，對比結果如表4 所示。

表4 不同模型預報值精度對比 單位：K

由表4 可知，Tm(China)模型的偏差值為1.648 5 K在三種模型中偏差值最大，均方根誤差與平均絕對誤差值也遠大于其余兩種模型。Tm(JN)模型的均方根誤差、平均絕對誤差、偏差分別為2.736 8、2.135 9、-0.013 7 K，小于Tm(Bevis)模型及Tm(China)模型。Tm(JN)模型與Tm(Bevis)模型的均方根誤差及平均絕對誤差基本接近，但前者精度仍略高。因此在濟南地區，使用構建的Tm(JN)模型與大氣加權平均溫度吻合度更好、精度更高，表現出更好的適用性，提高了濟南地區GNSS 反演PWV 的精度，可以應用于本地區的PWV 反演計算。

3.2 濟南加權平均溫度模型反演PWV 應用分析

為了進一步檢驗濟南加權平均溫度模型在該地區反演PWV 的精度，利用山東建筑大學連續運行參考站（continuously operating reference stations，CORS）SDJZ 站，2020 年1 月（年積日第1—31天共31 d）、2020 年7 月（年積日第182—212 天共31 d）的觀測數據，以及濟南加權平均溫度模型，對濟南地區的PWV 進行解算。為減弱對流層效應對解算結果的影響，引入三個國際GNSS 服務組織（International GNSS Service, IGS）站（即JFNG站、HKWS 站、LHAZ 站）的觀測數據組網解算。三個IGS 站、SDJZ CORS 站、濟南章丘區探空站站點位置分布如圖5 所示，其中SDJZ 站與章丘探空站相距約30 km。

圖5 IGS 站、SDJZ CORS 站、濟南章丘探空站站點位置

利用加米特（GAMIT）10.71 軟件進行PWV反演實驗，解算得到1 月份及7 月份SDJZ 站00:00、12:00 的ZWD 值，分別通過Tm(JN)模型以及Tm(Bevis)模型，計算得到相應的Tm(JN)的PWV 值、Tm(Bevis)模型的PWV 值，以RS/PWV 值作為參考值進行對比分析，如圖6 所示。

由圖6（a）可知，1 月份的濟南模型的PWV、Bevis 模型的PWV 基本重合，且RS 的PWV 的變化趨勢基本保持一致。以年積日第6 天為例，在有降水事件發生前，PWV 值會急劇增加，當降水結束時，又會迅速減小。由圖6（b）可知，7 月份的濟南模型的PWV、Bevis 模型的PWV 以及RS 的PWV 的變化趨勢同樣保持一致，在年積日第185天、第187 天、第195 天、第205 天、第209 天發生降水時，PWV 均發生迅速增加的現象，其中尤以第205 天最為明顯，降水發生前PWV 含量由21.15 mm 迅速增加至62.83 mm，由此可以判斷PWV 能夠為預報降水提供有力依據。

圖6 SDJZ 站大氣可降水量與實際降水關系

表5 為濟南模型的PWV、Bevis 模型的PWV的精度對比分析。

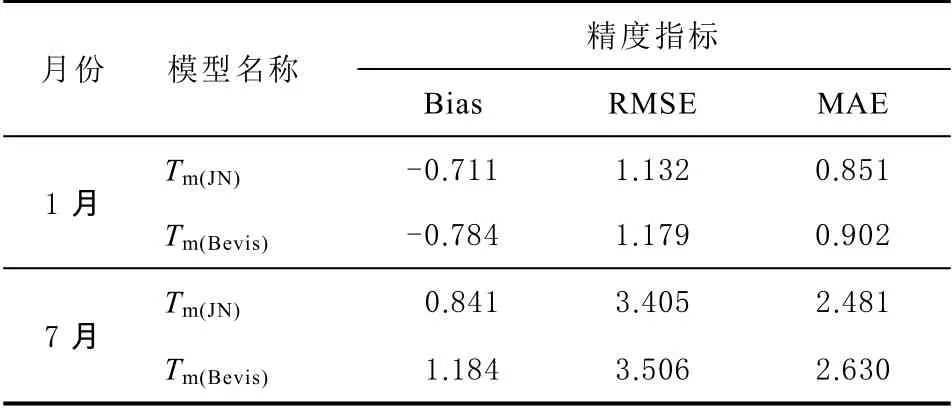
表5 濟南模型與Bevis 模型PWV 精度對比單位：mm

由表5 可知，1 月份的濟南模型的PWV 的偏差、均方根誤差、平均絕對誤差較Bevis 模型的PWV 分別降低0.07、0.04、0.05 mm；二者反演PWV精度大致相同，這可能與冬季天氣寒冷干燥，降水稀少有關，但Tm(JN)模型仍優于Tm(Bevis)模型。7 月份的濟南模型的PWV 的偏差、均方根誤差、平均絕對誤差較Bevis 模型的PWV 精度分別提高0.34、0.10、0.15 mm，與1 月份精度相比，濟南模型的反演精度有了較為明顯的提高。7 月份的均方根誤差、平均絕對誤差要明顯大于1 月份，這可能與夏季天氣濕熱多變，降雨頻繁，冬季天氣寒冷干燥有關。濟南模型7 月份的均方根誤差為3.405 mm，符合國際要求的3～4 mm 的精度要求[20]。通過以上精度對對比分析，本文構建的濟南模型比Bevis 模型精度更高，更適合本地PWV 反演。

4 結束語

本文利用懷俄明大學提供的章丘探空站2015—2019 年的探空資料，利用數值積分解算出大氣加權平均溫度與ERA-5 再分析資料建立符合濟南地區的加權平均溫度模型并與Bevis 模型、中國東部地區模型進行精度驗證與分析，得到下列結論：

1）Tm值小于Ts值，而且二者變化趨勢均滿足以一年為單位的周期循環，變化幅度也基本相同，在7 月達到峰值后逐月遞減。二者的相關系數為0.927 1，表現為線性強相關。根據逐月份Tm/Ts各相關參數可知，冬季各月份的均方根誤差分別為2.892、2.984、2.947 K，均大于全年的均方根誤差2.588 K；夏季各月份的均方根誤差分別為1.882、1.786、1.763 K，均小于全年的均方根誤差。冬季與夏季的均方根誤差的平均值分別為2.941、1.810 K，相差1.131 K。因此在進行反演大氣可降水量時，應選擇相應月份的模型進行反演實驗。

2）濟南加權平均溫度模型擬合值與真值間的殘差滿足正態分布，殘差區間-3～3 K 所占的比重為75%，±5 K 區間內的殘差為95%，濟南加權平均溫度模型擬合程度很高。

3）Tm(JN)模型與Tm(Bevis)模型、Tm(China)模型相比，偏差值減小了1.5 K 及1.9 K，均方根誤差精度分別提高了20%和21%、平均絕對誤差精度分別提高了25%和23%，表明Tm(JN)模型較Tm(Bevis)模型、Tm(China)模型在濟南地區的精度更高，可靠性更好。在外符合精度檢驗中，Tm(JN)模型均方根誤差、平均絕對誤差、偏差均小于其他兩種模型，精度略高于Tm(Bevis)模型，模型精度有所提高。Tm(JN)模型與大氣加權平均溫度吻合度更好、精度更高，表現出較好的適用性，可以應用于本地區的PWV反演計算。

4）利用章丘探空站數據及最小二乘原理對中國東部地區模型進行優化，優化后的中國東部地區模型精度較優化前有了大幅提高，其中均方根誤差精度提高 17.8%，平均絕對誤差精度提高25.5%。優化后的中國東部地區模型與濟南加權平均溫度模型精度大致相當，在濟南地區的適用性得到提高。

5）通過PWV 反演實驗，1 月份的反演實驗濟南模型的PWV 與Bevis 模型的PWV 反演PWV精度大致相同，這可能與冬季天氣寒冷干燥，降水稀少有關，但濟南模型仍優于Bevis 模型。7 月份濟南模型PWV 的偏差、均方根誤差、平均絕對誤差較Bevis 模型的PWV 精度分別提高0.34、0.10、0.15 mm。對于濟南地區PWV 解算而言，本文構建的濟南加權平均溫度模型更適合本地PWV 反演。