覆蓋件型面拉延筋參數化設計系統

種 亮，孔垂品，周雄輝

(上海交通大學 模具CAD國家工程研究中心，上海 200030)

0 引言

汽車覆蓋件多為空間自由曲面，其拉延成形是一個復雜的彈塑性形變過程，不合理的成形工藝參數、模具設計等很容易導致板料各處應力不均勻，從而造成零件不均勻變形，出現拉裂、起皺、回彈、厚度不均和變形量不足等缺陷[1]。在板料成形過程中，為控制材料的流動速度和流動方向，需要在壓料面局部位置設置拉延筋。不同類型的拉延筋會造成板料形變區的形變程度大小和分布的不同，為了有效控制材料的流動，避免各種缺陷的產生，需要合理設計拉延筋的位置、形狀和幾何參數[2]。拉延筋截面通常采用圓形、矩形和三角形等簡單形狀；按照拉延筋閉合與否，也可分為環拉延筋和線型拉延筋；可以是單條也可以是多條，其所在位置通常由凹模口線在壓料面向外偏置一定距離得到。

傳統拉延筋設計主要依靠工藝設計人員手工進行，再利用有限元模擬軟件不斷地校核和優化設計方案，屬于典型的試錯方法。該方法不僅效率低，而且最終工藝方案質量穩定性差，嚴重依賴于設計人員的經驗[3]。為此，國內外學者展開了廣泛的研究，開發了許多拉延筋設計系統。Chung[4-5]采用垂直截面掃掠的方法進行矩形或者圓形拉延筋參數化建模，他設計的拉延筋無沖壓負角的問題，并且非閉合筋的端頭光順處理也十分簡單快速。但是其拉延筋控制點的選取過少，并沒有完全覆蓋拉延筋線上所有的控制點，可能會降低設計精度。最嚴重的是，當拉延筋中心線曲率變化復雜時，經常會出現整個曲面不連續的情況，甚至導致建模失敗。熊洋等[6]提出了從建模到編輯修改的參數化設計方案，實現了拉延筋參數化設計。王振等[7]提出了面向自動化設計的拉延筋參數化建模方法，開發了拉延筋參數化設計系統，可以直接創建和編輯拉延筋，該種應用正交截面法創建的拉延筋不會出現沖壓負角的問題。還有一些研究人員[8-9]提出了將有限元技術和多目標優化方法結合的方法來指導拉延筋的自動化設計。但是很多當前的研究方法中，拉延筋主要采用了等效拉延筋模型[10]，只考慮了平面應變條件下板料流經拉延筋的形變模式，這樣造成拉延模擬精度偏低[11]。由于汽車覆蓋件形狀復雜，存在很多非平面應變區域和變截面形狀的拉延筋，在這些區域的板料形變不完全符合平面應變。采用真實的拉延筋模型，能準確反映拉延筋對板料的約束作用，有效提高拉延成形有限元分析的準確性，還可以直接用于拉延模具表面的數控加工，提升模具制造的效率。

本文研究開發了覆蓋件型面拉延筋參數化設計系統。采用自適應的曲線離散方法得到拉延筋控制點，基于垂直截面完成拉延筋截面線的幾何參數化設計，通過曲面掃掠結合端頭光順處理，創建了拉延筋曲面，實現了矩形、圓形和混合拉延筋的快速、準確的參數化建模。

1 拉延筋參數化模型與自動設計方案

1.1 拉延筋參數化模型

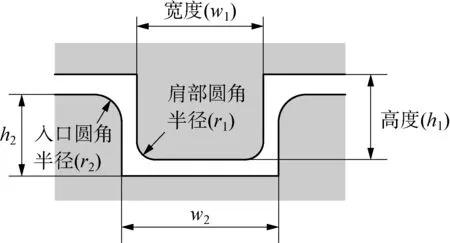
拉延筋的幾何形狀和參數，會影響板料流過拉延筋的流動形式，造成不同大小的拉延阻力。拉延筋幾何形狀是指拉延筋的截面形狀，如圖1所示，一般可分為圓形、矩形和三角形等。通常在企業生成中，拉延筋按照其所處位置不同，分為凸、凹筋，即凸模上的拉延筋叫筋；凹模上的則叫槽。拉延筋參數包括寬度(w)、高度(h)、肩部圓角半徑(r2)和入口圓角半徑(r2)4個參數。對于矩形筋來說，凹槽的寬

w2=w1+2t+2g

(1)

凹槽的高

h2=h1+t+g

(2)

其中，w1為凸筋的寬；h1為凸筋的高；t為板料厚度；g為凸凹筋間隙值。對于不閉合筋，還要加上端頭長度。在企業生產中，實際使用拉延筋時，需要設計凸凹筋配合使用，以達到使零件特定形變的目的，所以凸凹筋的中心線一定處于相同位置。根據覆蓋件的類型不同，通常會將拉延筋與幾種常見的筋槽配合使用，例如矩形筋矩形槽、圓筋矩形槽等。

(a) 矩形

(b) 圓形

此外，關于在曲面壓料面上拉延筋的幾何參數存在兩種不同的定義，如圖2所示。第一種定義拉延筋沿著沖壓方向的高為高度，拉延筋槽的長度為寬度，如圖2(a)所示；第二種定義垂直于拉延筋槽底部的高為高度，沿著水平軸的水平長度為寬，如圖2(b)所示。本文采用比較通用的第二種方式。

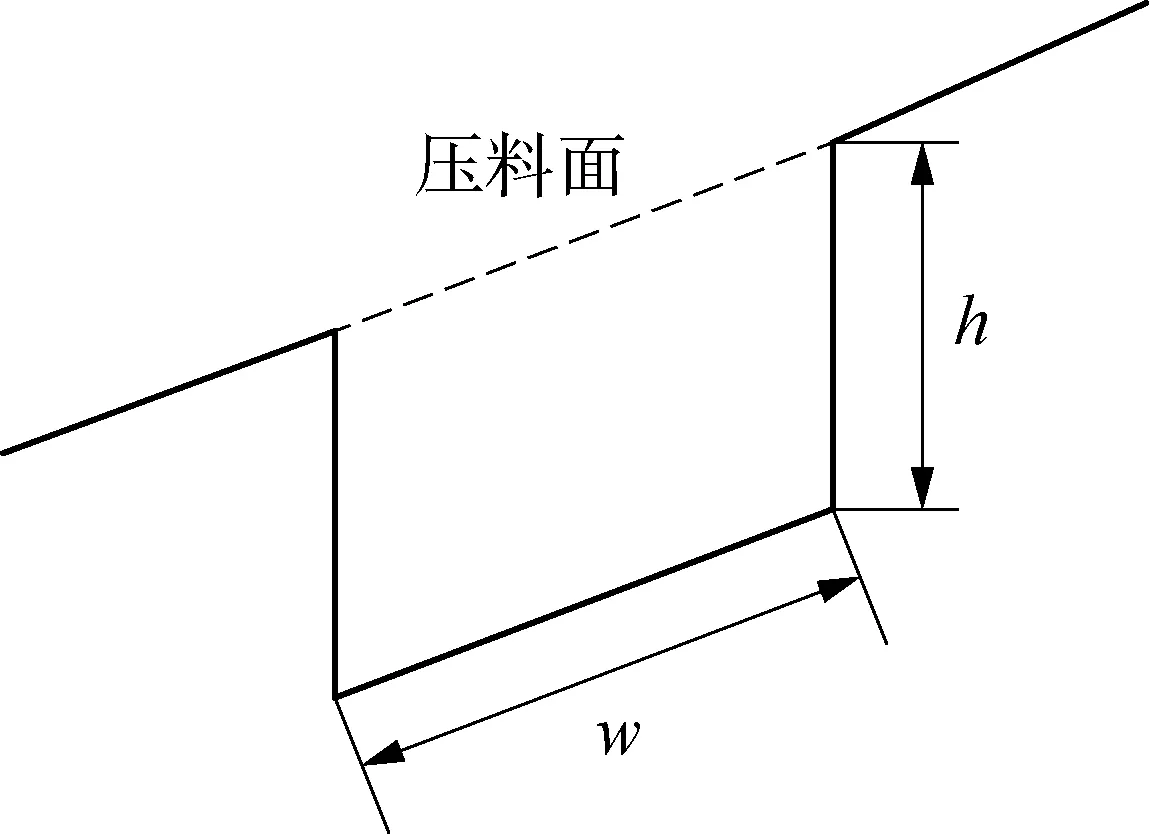
(a) 拉延筋沿沖壓方向為高

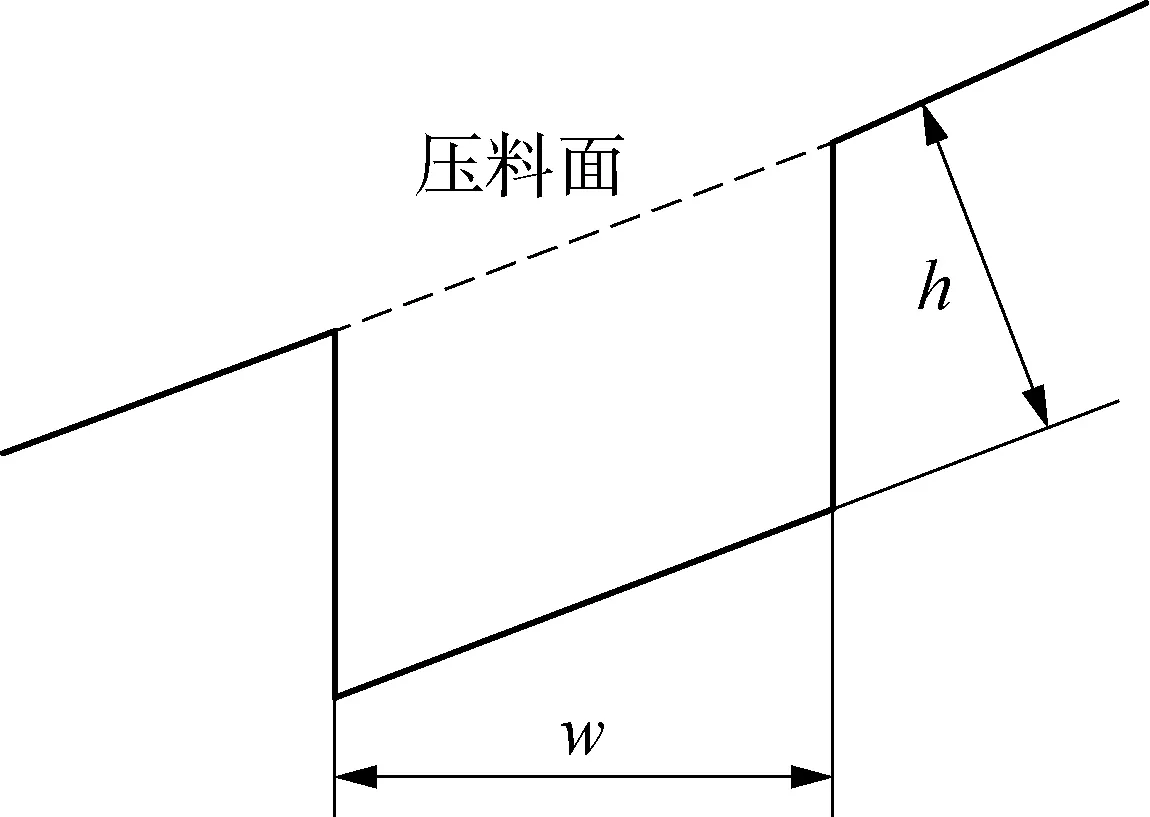
(b) 垂直拉延筋槽底為高

1.2 拉延筋自動設計方案

假設沖壓方向、拉延筋中心線和壓料面已知，提出了一種拉延筋自動化參數建模方案，流程如圖3所示，可以同時保證拉延筋建模的速度和精度。

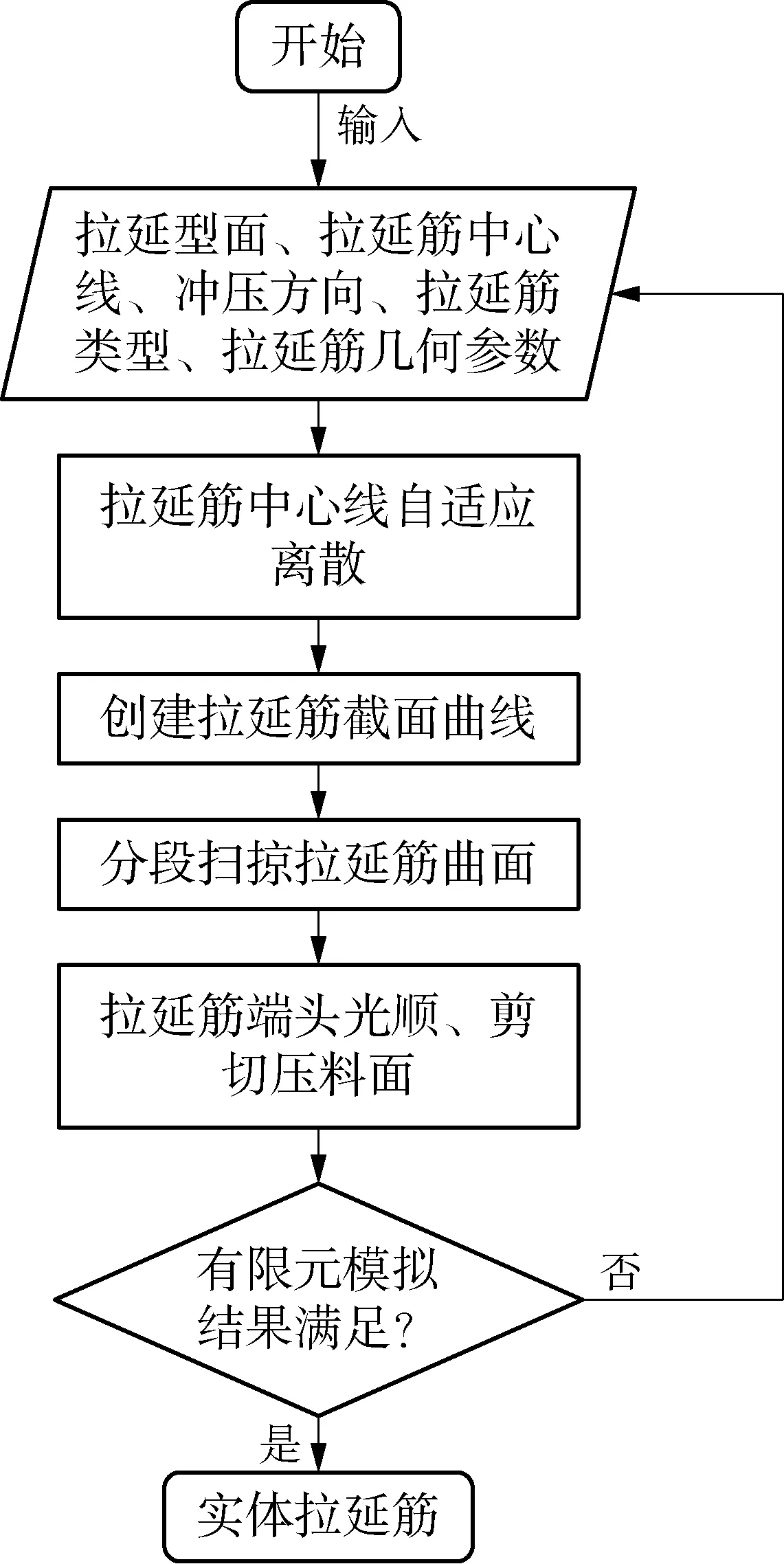
圖3 拉延筋幾何建模的流程

首先采用自適應的拉延筋中心線離散方法將中心線離散為一系列控制點，即生成拉延筋截面線所在的位置點。通過分析每個控制點的空間信息，得到該點下的局部坐標系和垂直截平面。根據用戶指定的該點的截面參數(拉延筋高、寬、高度余量等)和截面類型，利用坐標變換可以得到整體坐標系下的，截面線上端點的三維坐標。通過倒角等一系列操作得到每個控制點的截面曲線的形狀，利用曲面放樣分段創建實體拉延筋。最后對于非封閉的拉延筋，需要進行端頭光順處理和壓料面裁剪，即可得到最終的實體拉延筋。

2 拉延筋自動化設計關鍵技術

2.1 拉延中心線自適應離散

汽車覆蓋件的輪廓尺寸通常較大，其拉延筋布置的數量也比較多，有直拉延筋、環拉延筋和斜拉延筋等，故其拉延筋線較長，曲率變化復雜。此外，在同一段拉延筋中，也存在截面幾何形狀不同的拉延筋，它們在過渡部分的建模中會相互影響，這無疑增加了實體拉延筋建模的復雜性。在采用分段構建實體拉延筋的過程中，若離散距離取得過大，會造成在曲率半徑小的地方建模精度過低；若距離取得過小，則建模速度會降低。為了同時保證拉延筋的建模速度和精度，在離散得到拉延筋型質點的過程中，建立拉延筋線曲率半徑和離散距離的函數映射關系，如圖4所示： 當曲率半徑小于最小曲率半徑rmin時，離散距離保持恒定的最小值dmin；當曲率半徑在rmin～rmax之間時，采用線性插值的方法，得到不同的離散距離d；當曲率半徑大于于最大曲率半徑rmax時，離散距離保持恒定的最大值dmax。因此，當離散直線拉延筋或者其他拉延筋的直線部分時，由于拉延筋線比較平滑，拉延筋線的離散距離較大；而在彎曲部分，離散距離自動減小。該拉延筋線自適應的離散方法能較好地平衡拉延筋建模速度和精度。

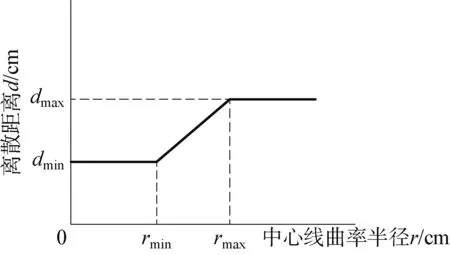
圖4 離散距離和中心線曲率半徑的關系

2.2 拉延筋垂直截面線的生成

本系統采用全參數化的拉延筋截面曲線來控制真實拉延筋的形狀，如圖5所示： 拉延筋中心線上的一點P，該點局部直角坐標系坐標軸為H，V，U，其中V定義為拉延筋截面線所在的局部坐標系的y軸；H定義為沖壓拉延方向單位矢量D和拉延筋中心線在P點的切向矢量T的叉乘；U定義為沖壓方向與H的叉乘，即：

(3)

(4)

圖5 拉延中心線上控制點P的截平面

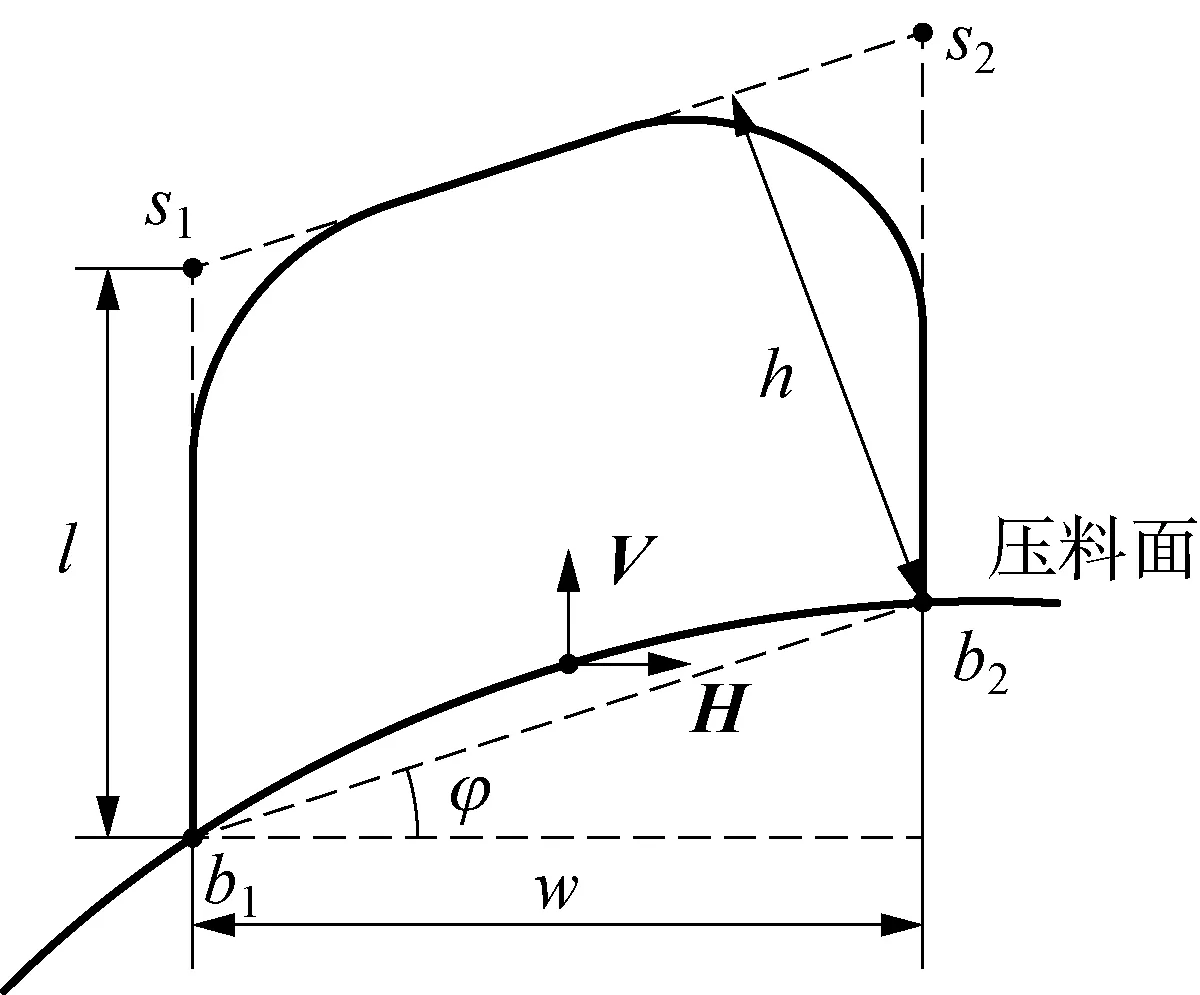
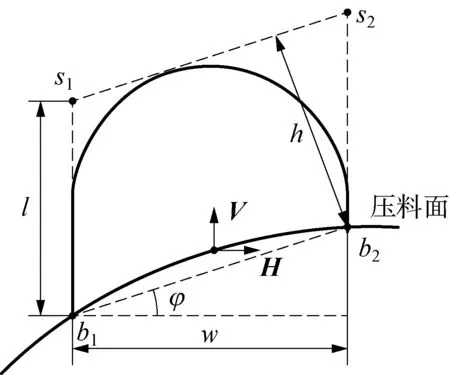
如圖6所示： 一個拉延筋截面線由4個邊界點定義，分別為b1，b2，s1，s2；其中，b1，b2通過投影在壓料面上確定：

(5)

(6)

(a) 矩形拉延筋

(b) 圓形拉延筋

其中，proj(|·)為沿著(·)方向在壓料面投影。為了避免創建的拉延筋存在著沖壓負角的問題，拉延筋肩部的s1，s2點通過沿著V方向移動距離l得到，即：

s1=b1+l·V

(7)

s2=b2-l·V

(8)

由上可得：

(9)

φ為V與水平軸的夾角。通常由于壓料面不是平面，所以l大于拉延筋實際的高。

2.3 混合拉延筋的生成與過渡

在拉延變形比較復雜的變形區域，通常需要在同一條拉延筋上的不同段產生不同的拉延阻力。除了修改對應拉延筋的寬、高和圓角半徑等參數外，還可以采用不同類型的拉延筋，所以經常會出現創建不同截面形狀的混合拉延筋。本系統通過截面形狀控制拉延筋類型，在需要過渡的部分，采用不同類型的拉延筋截面線控制混合拉延筋的生成與過渡，同時還采用曲面掃掠技術生成拉延筋，該方法可以克服不同截面類型拉延筋的光滑過渡問題，提高拉延筋創建的靈活性。

圖7是利用本方法創建的圓形和矩形拉延筋混合筋的實例，中間拉延筋截面線為圓形而兩端拉延筋截面線為矩形，所以拉延筋中間部分為圓形拉延筋，而兩端均為矩形拉延筋。將不同拉延截面線結合拉延筋位置中心線作為控制方法，采用NX自帶的曲面掃掠完成不同類型拉延筋的過渡，可以看出生成的各段拉延筋曲面質量好，過渡區域水平相切過渡，證實了該方法的有效性。

圖7 混合拉延筋創建實例

2.4 端頭光順設計

對于非閉合的拉延筋來說，拉延筋端頭的光順也是十分重要的。為保證拉延筋與壓料面的平滑過渡，以圖8所示的平面料面上的拉延筋為例，來說明本系統采用的拉延筋端頭光順方法。圖8中，在距離拉延筋端點P0長度的P點，創建一段與原來端頭拉延筋中心線P(t)相切的曲線Q(t)，代替原來的拉延筋端頭曲線。

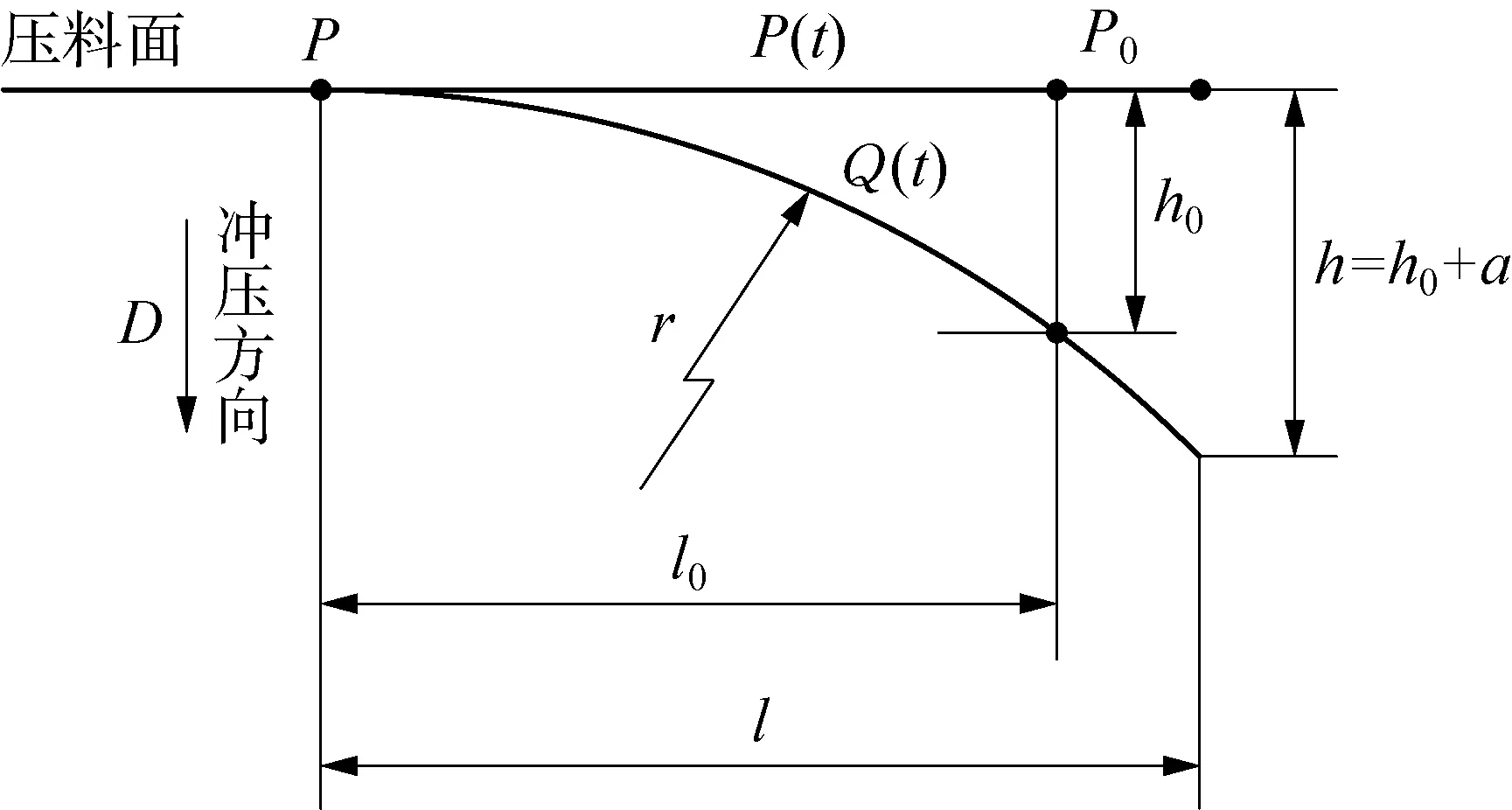
圖8 拉延筋端頭光順處理示意圖

根據設定的端頭的長度和拉延筋的高度，新的端頭曲線Q(t)的半徑

(10)

(11)

其中，h=h0+a，a為高度的余量，對于平面壓料面上的拉延筋，a=0；其他大部分情況，拉延筋通常被布置在曲面壓料面上，故a>0，由于壓料面的曲率不是特別大，所以通常a取10～20。圖9為利用本系統采用的光順方法，創建實體拉延筋的端頭圖。由圖10可知： 拉延筋的端頭與壓料面平滑過渡，符合實際的需求。

(a) 矩形

(b) 圓形

3 系統實現與誤差分析

3.1 系統實現

為了驗證所提出方法的可行性，基于NX 11.0平臺，采用NX的二次開發技術，開發了覆蓋件型面拉延筋參數化設計系統。該系統可以用于矩形拉延筋和圓形拉延筋的自動生成，且參數設置簡單，并進行了大量的汽車覆蓋件拉延筋建模的測試，所得實體拉延筋質量好。圖10為拉延筋設計系統界面，該系統界面包含壓料面、沖壓方向、拉延中心線和拉延筋類型的選擇輸入、拉延筋幾何參數輸入，和板料、端頭長度和尺寸公差的設定。

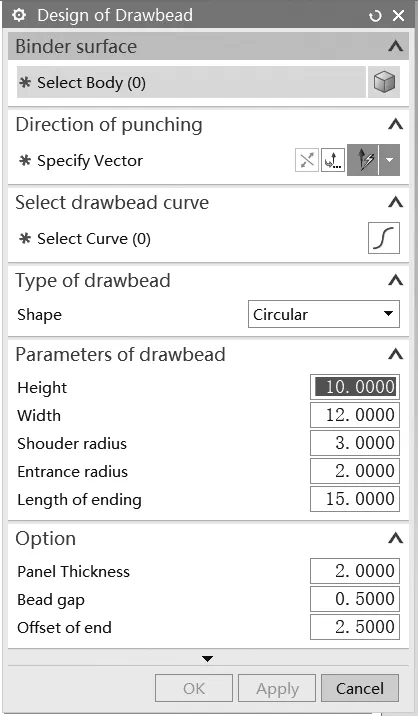
圖10 拉延筋設計系統界面

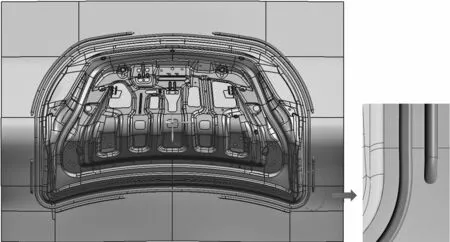
圖11 拉延筋設計實例

圖11展示了使用本系統生成的某汽車后蓋內板拉延型面實體拉延筋的三維幾何模型，該建模過程只需要簡單的幾步人工交互，建模時長僅需數分鐘。該模型的拉延筋包括1段環矩形拉延筋、2段直線圓形拉延筋、4段斜圓形拉延筋。該拉延筋面光順，無沖壓負角，可直接用于拉延模面設計、實體拉延筋的有限元模擬和拉延筋的計算機數字控制機床(computer numerical control, CNC)加工。該實例驗證了本系統的實用性和有效性。

3.2 誤差分析

采用本系統創建的實體拉延筋的真實高度和給定的值存在一定的偏差，壓料面的曲率半徑越大，其誤差越大。如圖12所示： 假設在拉延筋中心P處，壓料面為凹曲面，那么真實的拉延筋的高度比實際設定的拉延筋高度小，最大誤差為：

(12)

其中，r為在壓料面上點P處的曲率半徑；θ為曲線傾角。相反，如果點P所在的壓料面為凸曲面，那么拉延筋實際的高度比設定的拉延筋的高度大。但在實際案例中，高度偏差可以忽略。假如曲率半徑r為600 mm，傾角θ為20°，拉延筋高為6 mm，則最大的高度誤差僅為0.004 mm，所以在壓料面不是很彎曲，且拉延筋線傾角不是很大的情況下，其產生的高度誤差是非常小的，可以忽略。

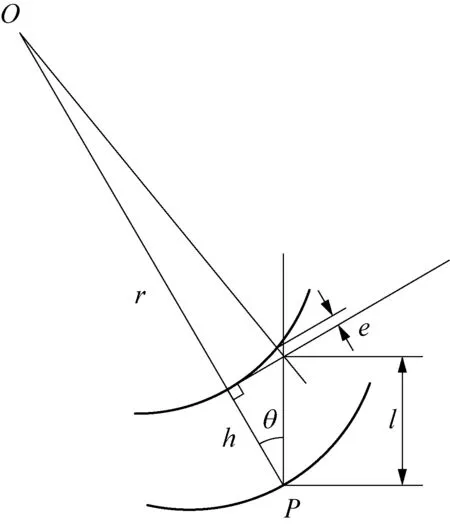
圖12 拉延筋高度誤差

4 結論

本文分析了汽車覆蓋件拉延筋的設計方法，提出了基于垂直截面的分段截面線放樣曲面的拉延筋建模方法，該方法準確度高，穩定性好。開發了實體拉延筋設計系統，用大量的實例驗證了方法的正確性和系統的可行性。該系統能方便、準確地生成各種類型的拉延筋，拉延筋表面質量高、端頭光順，混合筋過渡段平滑，可以直接用于實體拉延筋的有限元仿真和制造，有效地提高了覆蓋件拉延筋設計的效率。