酰化膠原溶液的流變行為研究*

李從虎，龍槿彥，吳 彥，胡佳慧，李國英，李文娟

(1.四川大學 皮革化學與工程教育部重點實驗室，成都 610065；2.安慶師范大學 生命科學學院，安徽 安慶 246133)

0 引 言

膠原是一種天然大分子產物，廣泛存在于動物的皮膚、軟骨等結締組織中，因具有良好的生物相容性、細胞吸附性和低免疫原性等優(yōu)良特性而廣泛應用于食品、生物醫(yī)藥和組織工程等領域[1]。受到剪切力的作用，將膠原溶液制備成凝膠、海綿、膜、纖維等產品時，其粘彈性、抗變性能等理化特性會發(fā)生改變，最終影響到膠原產品的性質和外觀[2]。由于流變學可以準確地反映蛋白質等天然大分子在生產和加工過程中受外力作用而發(fā)生的形變，因此，對膠原溶液的流變性能進行系統(tǒng)的研究，揭示其內部結構與力學響應之間的規(guī)律，對獲得穩(wěn)定的膠原產品具有十分重要的意義。

近年來，對膠原及其衍生物的流變行為的研究已有一定的報道。Ding等將羧甲基纖維素鈉引入到膠原溶液(8 mg/mL)中，其流動性能顯著提升[3]。Yang等人發(fā)現冪律方程、Carreau模型可有效擬合膠原溶液的穩(wěn)態(tài)流動曲線[4]。Chen等考察了己二酸-NHS酯(NHS-AA)對堿溶膠原溶液的流變性能，結果表明隨著NHS-AA濃度的升高到1.5 mmol/L時，溶液的彈性模量、粘性模量和復數粘度不斷增大；隨后，隨著NHS-AA濃度的繼續(xù)升高，溶液彈性模量、粘性模量和復數粘度反而下降[5]。作為一種蛋白質，膠原溶液的流動性能對溫度十分敏感。段煉等研究了溫度對膠原溶液的穩(wěn)態(tài)流變性能的影響，發(fā)現膠原溶液具有明顯的假塑性，溫度升高剪切粘度卻下降[6]。

然而天然膠原難以在中性條件下溶解，且表面活性較低，限制了其應用。若天然膠原能夠自身形成膠束等表面活性劑締合體系，則可將親脂藥物包裹在聚集體內，不僅對藥物起到增溶、保護和穩(wěn)定作用，還對控制藥物的緩釋具有重要的意義。因此，作者在膠原的側鏈引入了疏水的月桂酰殘基和親水的琥珀酰殘基，制備得到一種具有兩親結構的酰化膠原，其結構示意圖如圖1所示[7]。酰化膠原不僅保持了天然膠原的生物活性，還提升了表面性質[8-9]。在酰化膠原溶液的存儲、生產和應用時，其流動性能必然會受到溫度的影響。因此，本文主要研究了酰化膠原溶液的穩(wěn)態(tài)剪切粘度、動態(tài)頻率掃描、蠕變以及觸變行為，并對其流動曲線進行了數學模擬，以期為該產品的生產和應用提供理論依據。

圖1 酰化膠原示意圖[7]Fig 1 Structural scheme of acylated collagen[7]

1 實 驗

1.1 實驗儀器

流變儀：MarsⅢ型，德國Haake公司。

1.2 酰化膠原水溶液的制備

按照文獻[7]制備酰化膠原，將酰化膠原海綿溶解于0.01 mol/L的PBS(pH7.4)中，制備得到7.5 mg/mL的酰化膠原溶液，在4 ℃下保存?zhèn)溆谩?/p>

1.3 穩(wěn)態(tài)流變測試

采用流變儀和錐板模式(外錐角為1°，直徑為35 mm，板間距為0.053 mm)，選用粘度法模式，在控制速率的條件下測試酰化膠原溶液的穩(wěn)態(tài)流變性能，其中溫度范圍分別為25、27.5和30 ℃，剪切速率γ范圍為0.01～100 s-1。

1.4 動態(tài)流變測試

采用流變儀和錐板模式(外錐角為1°，直徑為35 mm，板間距為0.053 mm)，并在動態(tài)測試中選擇應力控制模式下，研究酰化膠原溶液的粘彈性行為，測定彈性模量(G′)、粘性模量(G″)、復數粘度(η*)和內耗(tanδ)隨著頻率的變化。測試溫度分別為25、27.5和30 ℃，應變?yōu)?%，動態(tài)頻率0.01～10 Hz。

1.5 蠕變測試

將制備的酰化膠原溶液置于流變儀的錐-板夾具中(外錐角為1°，直徑為35 mm，板間距為0.053 mm)。分別在25、27.5和30 ℃下，對其施加1 Pa的應力并持續(xù)100 s，記錄其蠕變狀況。隨后，在接下來的400 s里去除樣品上施加的應力，使其慢慢回復，記錄其回復狀況。

1.6 觸變測試

分別在25、27.5和30 ℃條件下，將制備的酰化膠原溶液置于流變儀的錐-板夾具中(外錐角為1°，直徑為35 mm，板間距為0.053 mm)。設置剪切速率在150 s內從0.01 s-1增大到50 s-1，然后剪切速率在接下來的150 s內從50 s-1降低到0.01 s-1。

1.7 數學模擬

采用冪率方程、Carreau和Cross方程對不同溫度的酰化膠原溶液的穩(wěn)態(tài)剪切曲線進行擬合[10-11]；采用Leonov模型對酰化膠原溶液的動態(tài)頻率曲線進行擬合[12]；采用Burger模型對蠕變曲線進行擬合[13]；采用Herschel-Bulkley方程對觸變測試曲線進行擬合[14]。

其中，

冪率方程：

η=Kγn-1

(1)

式(1)為冪率方程的關系式，其中η是剪切粘度(Pa·s)，γ是剪切速率(s-1)，K是粘度指數，n為材料的非牛頓指數。

Carreau方程：

(η-η∞)/(η0-η∞)=[1+(λγ)2](q-1)/2

(2)

式(2)中，η是剪切粘度(Pa·s)，η0為零剪切粘度(Pa·s)，η∞為無窮剪切粘度(Pa·s)，γ是剪切速率(s-1)，n為材料的非牛頓指數，λ為體系常數。

Cross方程：

(3)

式(3)中，η是剪切粘度(Pa·s)，η0為零剪切粘度(Pa·s)，η∞為無窮剪切粘度(Pa·s)，α為特征弛豫時間(s)，m為材料常數。

Leonov方程：

(4)

(5)

式(4)和(5)中，Ωk=ωθk,θk代表在第k次松弛模型的松弛時間，ω和m0分別代表頻率和材料常數。

Burger方程：

γ(t)=σ0t/η0+σ0/G0+σ(1-e-t/λ/G1)

(6)

式(6)中，G0和G1都表示彈性系數，但G0反映酰化膠原溶液在應力作用下抗形變的能力，而G1主要是阻止粘性原件的變形；σ0和η0分別代表應力和產生不可回復殘留變形的粘性系數；λ是回復的延遲時間。

Herschel-Bulkley方程：

τ=τ0+βγa

(7)

式(7)中，τ0是屈服應力，β和a分別是材料參數和冪指數。

2 結果與討論

2.1 穩(wěn)態(tài)流變測試

圖2揭示了酰化膠原溶液在25、27.5和30 ℃條件下的穩(wěn)態(tài)剪切曲線。由圖可知，隨著溫度的升高，酰化膠原溶液的剪切粘度呈現降低的趨勢。這是因為隨著溫度的升高，酰化膠原分子的無規(guī)則熱運動增大，其聚集體逐漸松散，使得粘度逐漸下降[6]。從圖中還可以看出，在測試溫度范圍內，酰化膠原溶液的粘度都隨剪切速率的增加而減小，表現為剪切變稀行為[15]。這是因為剪切力增大，酰化膠原分子之間的相互作用力減弱，使得溶液的流動性逐漸增加[4]。

圖2 酰化膠原溶液剪切粘度和剪切速率的關系Fig 2 Relationship between the viscosity (η)and the shear rate of acylated collagen solutions

表1所示為采用冪律方程擬合酰化膠原溶液的穩(wěn)態(tài)流變測試曲線參數。由表可知，擬合的相關系數R2均接近于1.0，表明該模型擬合效果較好。不同溫度條件下，n值小于1，表明酰化膠原溶液具有假塑性。隨著溫度的升高，n值不斷上升但K值逐漸下降，表明酰化膠原溶液的假塑性和粘度隨溫度的升高而不斷降低。擬合結果與實際測試結果相似，這是因為溫度升高，分子運動加快，分子之間的摩擦力和聚集體的纏結力不斷降低，導致酰化膠原的假塑性和粘度出現降低的趨勢。

表1 酰化膠原溶液在不同溫度下冪率方程擬合得到的參數Table 1 Parameters from Power law model fitting ofacylated collagen solutions at different temperatures

表2和3所示為酰化膠原溶液在不同溫度下Carreau和Cross方程擬合得到的參數。由表可知，用Carreau和Cross方程擬合得到的相關系數R2都接近于1，表明Carreau和Cross方程都能夠準確的描述酰化膠原溶液的剪切流動。Carreau與Cross方程中預測的零剪切粘度都是隨著溫度的上升而減小，說明溫度升高酰化膠原溶液的假塑性越弱，與穩(wěn)態(tài)剪切的實驗結果相符合。然而無窮剪切粘度非常小，這是因為當剪切速率非常高時，酰化膠原聚集體已經解聚成單分子，溶液的流動已經非常不穩(wěn)定，甚至被破壞，導致無窮剪切粘度非常小[16]。

表2 酰化膠原溶液在不同溫度下Carreau方程擬合得到的參數Table 2 Parameters from Carreau model fitting of acylated collagen solutions at different temperatures

表3 酰化膠原溶液在不同溫度下Cross方程擬合得到的參數Table 3 Parameters from Cross model fitting ofacylated collagen solutions at different temperatures

2.2 動態(tài)流變測試

在動態(tài)頻率測試中，彈性模量(G′)和粘性模量(G″)可以提供材料在液—固間響應的結構特性的重要信息[10]。圖3所示為酰化膠原溶液在不同溫度條件下的動態(tài)模量曲線。在所測試的溫度下，酰化膠原溶液均具有末端區(qū)和高彈區(qū)。G′和G″隨著溫度的升高而降低，但隨著頻率的上升而呈逐漸增大。在低頻下(G′G″)，酰化膠原溶液以彈性行為為主。隨著溫度的上升，交叉點(G′=G″)頻率也逐漸從0.037 Hz升高到0.160 Hz，表明在酰化膠原分子的松弛速率隨溫度的升高而加快，即松弛時間隨溫度升高而縮短。當溫度升高時，相鄰分子鏈CO和NH之間的氫鍵被破壞[17]，酰化膠原分子的熱運動能量增加，體系中分子之間的自由體積增大，使鏈段躍遷速度加快，并且形成的聚集體減小。

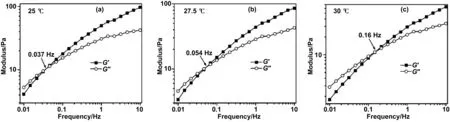
圖3 不同溫度下酰化膠原溶液的動態(tài)模量曲線Fig 3 Dynamic modulus of acylated collagen solutions at different temperatures

圖4所示為不同溫度下酰化膠原溶液的復數粘度和損耗因子曲線。由圖可知，酰化膠原溶液的復數粘度隨溫度的升高而降低，隨頻率的增加而降低。這一趨勢與穩(wěn)態(tài)剪切測試中酰化膠原溶液發(fā)生的剪切變稀是一致的。溫度的升高使分子之間的變換加快并減少分子之間的吸引力。然而在溶液體系中，分子之間的吸引力比分子之間的變換要強得多，因此粘度會隨溫度的升高而降低[18]。損耗因子(tanδ)是指G″與G′的比值(tanδ=G″/G′)。因此，當tanδ>1時，高分子溶液中的G″大于G′，所以該體系為粘性特征占優(yōu)勢；當tanδ<1時，高分子溶液中的G″小于G′，所以該體系為彈性特征占優(yōu)勢[19]。酰化膠原溶液的tanδ隨著溫度的升高而上升，表明酰化膠原溶液的粘性特征隨著溫度的升高而越來越強，這是因為溫度上升，酰化膠原溶液的流動性更強。

圖4 不同溫度下酰化膠原溶液復數粘度(a)和損耗因子(b)Fig 4 Complex viscosity and loss factor of acylated collagen solution under different temperatures

表4為酰化膠原溶液在不同溫度條件下采用Lenovo方程進行動態(tài)頻率測試擬合得到的參數。可見，Lenovo模型對酰化膠原溶液的動態(tài)頻率曲線具有較好的擬合效果(R2≈1.0)。隨著溫度的升高，ηk值不斷降低，表明酰化膠原溶液的粘度隨溫度升高而呈降低趨勢。擬合結果與實驗結果相符，這是因為溫度的升高，使分子間的相互作用力減弱，分子運動能力增強，導致酰化膠原溶液的流動性升高。

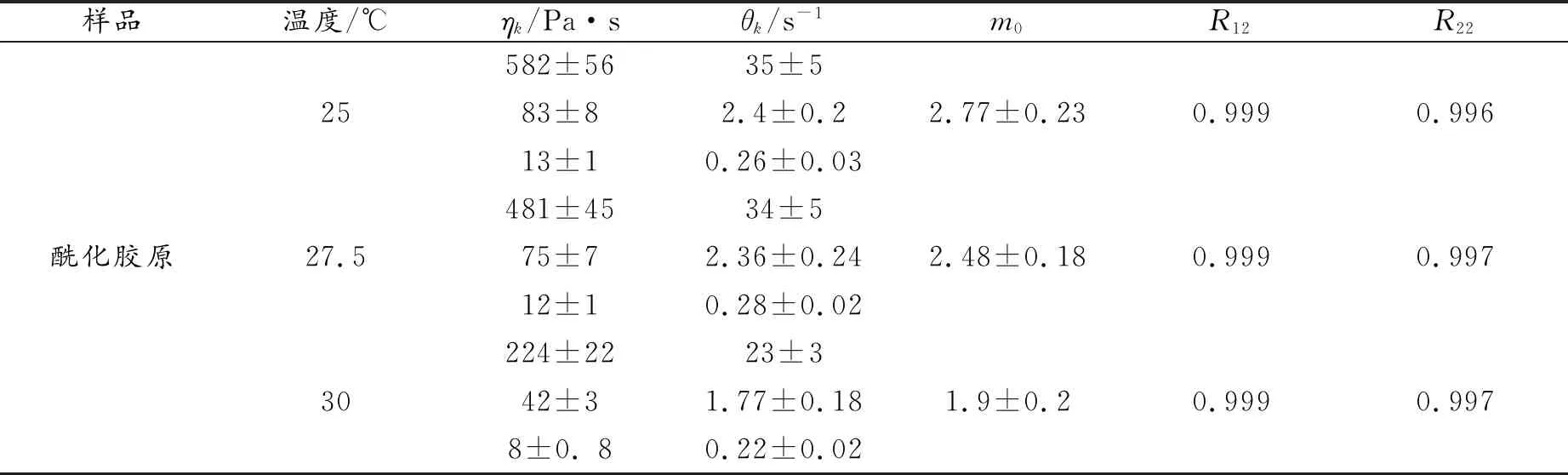
表4 酰化膠原溶液在不同溫度下Leonov方程擬合得到的參數Table 4 Parameters from theLeonov model fitting of the acylated collagen solutions at different temperatures

2.3 蠕變測試

圖5是對酰化膠原溶液在不同溫度條件下施加1 Pa的應力所測得的蠕變曲線。從圖中可以看出，酰化膠原溶液在所測試的溫度范圍內都表現出典型的蠕變行為，都具有可回復應變和不可回復應變。因此，在所測試溫度范圍內，酰化膠原溶液依然具有普彈形變、高彈形變和粘性流動響應，并表現出明顯的粘彈性。通常，柔量越大表明材料抵抗變形的能力越弱[20]。對酰化膠原溶液施加1 Pa的應力持續(xù)100 s后，柔量隨溫度的升高而逐漸降低，表明酰化膠原溶液在低溫下具有較強的抵抗變形的能力。這是因為隨著溫度的升高，酰化膠原分子的熱運動增加，聚集體減小，使其更容易發(fā)生形變，最終導致其抵抗形變的能力變弱。當外力去除后，隨著溫度的升高，酰化膠原溶液均出現回復現象，其回復部分占最大柔量的比值從31%降低到26%，表明酰化膠原溶液發(fā)生形變后所能回復的應變越小，在應力作用下發(fā)生粘性流動所占的比例也越大。

圖5 不同溫度下酰化膠原溶液的蠕變測試曲線Fig 5 Creep curves of acylated collagen solutions at different temperatures

圖6為酰化膠原溶液在不同溫度條件通過Burger模型對蠕變階段的擬合示意圖。結果發(fā)現Burger模型可以有效描述酰化膠原溶液抵抗變形的能力。通過模型可以預測，隨著溫度的升高，由于分子間的相互作用力減弱，導致酰化膠原溶液的彈性響應和抵抗變形的能力逐漸降低。

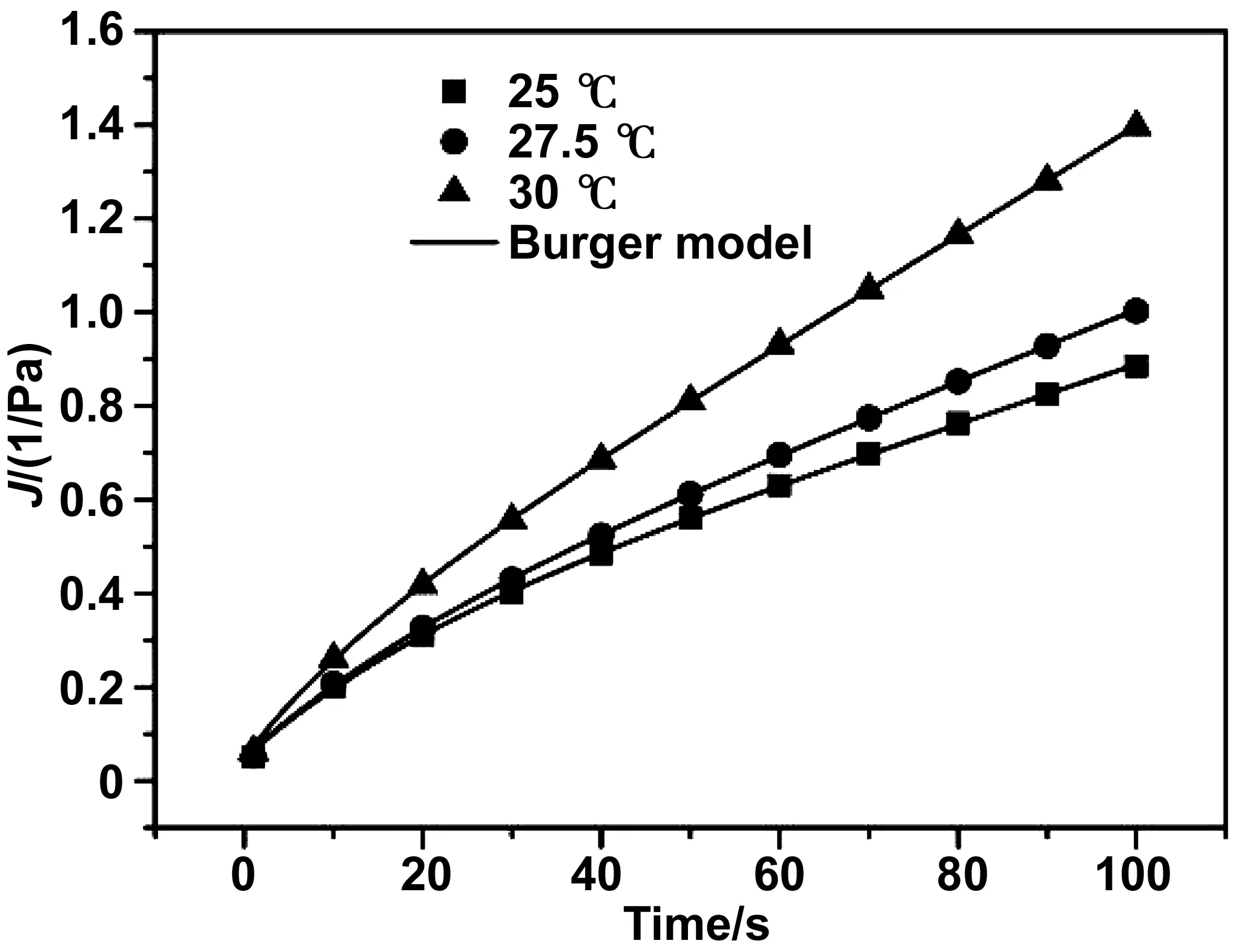
圖6 Burger模型對酰化膠原溶液在不同溫度條件下蠕變曲線的擬合Fig 6 Creep curves of acylated collagen solutions simulated by the Burger model at different temperatures

2.4 觸變測試

圖7是酰化膠原溶液在不同溫度條件下的觸變環(huán)曲線。由圖可見，觸變環(huán)面積未見明顯改變，可能是因為所測試溫度范圍較小。然而，在50 s-1的剪切速率下，其剪應力由52 Pa降低到41 Pa，表明酰化膠原溶液的粘度隨溫度升高而降低。隨著剪切速率的增加，酰化膠原分子纏結形成的網絡結構被破壞。當剪切速率逐漸降低時，酰化膠原分子結構逐漸回復。由于這種回復程度小于分子結構的破壞速率，導致酰化膠原觸變曲線的上行線和下行線不重疊[21]。

圖7 酰化膠原溶液在不同溫度下的觸變環(huán)曲線Fig 7 Thixotropic loop of acylated collagen solutions at different temperatures

圖8是使用Herschel-Bulkley方程對酰化膠原溶液在25 ℃條件下觸變測試的上行線和下行線分別進行的擬合示意圖。可以看出，Herschel-Bulkley方程的擬合曲線與實驗數據曲線可以較好的重合，且擬合的相關系數R2均接近于1.0。

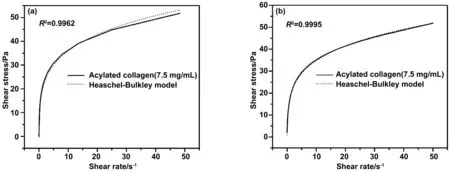
圖8 Herschel-Bulkley方程對酰化膠原溶液觸變環(huán)曲線的上行線(a)和下行線(b)的擬合(25 ℃)Fig 8 Up curve and down curve of CBS solution (7.5 mg/mL)and simulated curves from Herschel-Bulkley model (25 ℃)

3 結 論

以一種新型的酰化膠原為研究對象，采用流變學方法研究其溶液的流變行為，得到以下結論：

(1)酰化膠原溶液屬于假塑性流體，隨著剪切速率的增大，表現出明顯的剪切變稀行為。

(2)隨著溫度的升高，酰化膠原溶液的粘度、觸變性和抵抗變形的能力降低。

(3)冪律方程、Carreau方程、Cross方程、Leonov方程、Burger模型和Herschel-Bulkley方程可以有效擬合酰化膠原溶液的流變曲線。