Comp.B含能材料落錘沖擊應力特性分析

屈雪蕊

(西安航空學院 教務處，西安 710077)

0 引言

含能材料是指在一定的外界能量刺激下，能自身發生強烈的氧化還原反應，同時可以釋放出大量能量的物質。含能材料是許多領域研究的熱點問題[1-5]。從軍事用途上來看，一般意義上的含能材料主要包括發射藥、推進劑、猛炸藥、起爆藥等，是武器殺傷力和動力推進系統的主要能量來源[6]。近年來，世界軍事技術迅猛發展，精確打擊、高效毀傷能力和高生存能力是現代武器裝備追求的目標。要實現這些目標，作為武器能量載體的含能材料必須滿足高能量密度、低易損性和環境適應性的要求。

通常，含能材料的服役環境非常復雜，在生產、加工、運輸、儲存、發射、穿靶、破片等意外撞擊時，均處于不同的加載速率、不同的應力狀態和不同的溫度之中，有時需要承受很高的沖擊載荷，可見，復雜的服役環境對含能材料的安全性要求也越來越高[7]。

含能材料在動態沖擊下的力學性能響應也是軍事領域研究的重要問題之一。通過含能材料在動態沖擊下響應的研究有助于了解含能材料的動態響應特性和起爆機理，使之在需要起爆時能正常起爆，在不需要起爆的時候不會因為意外沖擊引起爆炸造成嚴重后果，這對于指導彈藥設計，提高彈藥的防護能力及運輸儲存的安全性具有非常重要的意義[8]。本文以常用的Comp.B炸藥為分析對象，對其動態沖擊相應特性進行分析。

1 實驗模擬系統

實驗采用含能材料沖擊實驗常用的落錘沖擊加載模擬系統，其實驗裝置示意圖如圖1所示。該系統主要是針對炸藥裝藥在火炮發射過程中的受力情況而建立起來的，可以很好地模擬火炮發射時的膛內加載特性。落錘通過活塞實現對炸藥裝藥的應力加載，系統中模擬受力的部分由上活塞、下活塞、上墊片、下墊片、藥柱、套筒和底座構成。其中：活寒、底座和套筒的材料采用T10鋼；藥柱材料為Comp.B炸藥；墊片材料為聚四氟乙烯，主要是為了吸收沖擊過程中所產生的高頻干擾波。通過支撐臺內的應力傳感器測得落錘在指定落高下炸藥未發生爆炸情況下底部的應力曲線。

圖1 落錘沖擊裝置示意圖

2 理論模型

Johnson-Cook本構模型(簡稱為J-C模型)一般用于描述大應變、高應變率、高溫環境下金屬材料的強度極限以及失效過程[9]。在J-C強度模型中，屈服應力由應變、應變率以及溫度決定。通常情況下，一種簡單的經驗式的本構方程可以表示為：

σ=f(ε)g(ε)

(1)

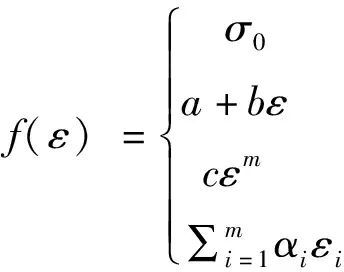
(2)

(3)

式中：σ為應力；ε為塑性應變；a、b、c、m、n和K為J-C模型與材料有關的常數。

由式(1)～式(3)可知，只有當應變率出現量級上的變化時，應變率對流動應力才會有顯著的影響。在應變率比較低或者常應變率條件下，材料的強化通常可以用冪函數強化模型來表示，其表達式如下：

σ=σ0+kεn

(4)

式中：σ0為屈服強度；k和n為與材料有關的常數。

雖然應力是一個二階矢量，但在一些條件下是可以將其看成一個標量，通過下式可將應力應變轉化為“有效”應力和“有效”應變：

(5)

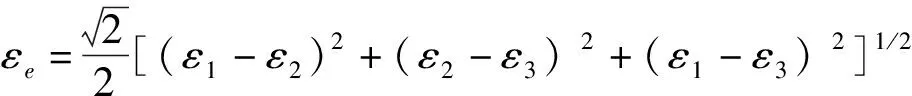
(6)

式中：σ1、σ2和σ3分別為空間三個方向上的主應力；ε1、ε2和ε3分別為空間三個方向上的主應變。這樣就將復雜的二維應變和應變率張量利用簡單的標量形式表達了出來。

實驗研究表明，Comp.B炸藥是一種脆性材料，不過其力學性能與應變率相關，具有明顯的應變率效應[10]。此外，應變速率相關的J-C模型比較精準的描述了多種材料的動態力學特性，較好的反映了材料的加工硬化，應變率效應，是一種行之有效并且被廣泛應用于工程實際問題的本構模型[11]。據此，本文采用應變速率相關的J-C模型來分析Comp.B炸藥受到沖擊時的應力、應變、應變速率和溫度之間的關系，其表達式如下：

(7)

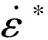
由式(7)可知應力由三部分組成，第一部分反應材料的應變硬化效應，第二部分反應應變率對材料力學性能的影響，第三部分反應溫度軟化效應。當溫度T為室溫時，T*=0，則式(7)可以簡化為

伍姍姍最樂于看到的醫患和諧場景是：為患者營造溫馨、方便、安全的就醫環境；為醫務人員營造開放、公平、非懲罰性的安全事件報告通路，分享錯誤并實時從中學習；多部門協助，積極、主動處理接受各類安全不良事件，有改進，有提高，有創新，保證患者安全，醫務人員安全。

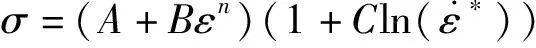
(8)

室溫下分析Comp.B炸藥受到沖擊時的情形可采用式(8)進行分析。在室溫條件下，采用圖1所示的實驗裝置進行實驗，通過對實驗的結果分析即可擬合出式(8)中的參數A、B、C和n，在此基礎上，利用數值計算軟件對室溫下Comp.B炸藥受到沖擊時動態響應過程進行分析。

3 數值建模

可用于應力應變分析的軟件有多種。其中，LS-DYNA軟件是功能齊全的幾何非線性、材料非線性并涉及多種接觸類型分析的有效工具，其分析計算的可靠性已經被試驗所證明，在工程應用領域也是被廣泛認可為最佳的分析軟件[12]，因此，本文選用LS-DYNA軟件對Comp.B炸藥受到沖擊時響應進行分析。

圖2所示為有限元分析的幾何模型及網格劃分圖，圖中的網格劃分采用SOLID164單元。SOLID164單元是三維的顯式結構實體單元，該單元自身為六面體結構，由8個節點構成，專門用于顯式動力學分析，支持非線性特性，其支持的材料包括彈塑性流體動力材料、彈黏塑性熱力學材料和Johnson-Cook彈塑性材料等。由于實體模型為軸對稱結構，劃分網格時采用映射網格劃分方式。

圖2 有限元分析模型及網格劃分圖

模擬計算使用的參數如下：藥筒尺寸為?60 mm×60 mm；實驗中落錘的重量分別為40 kg和400 kg；落高分別為1000 mm和1500 mm。表1中所示為計算所用的其他物性參數。

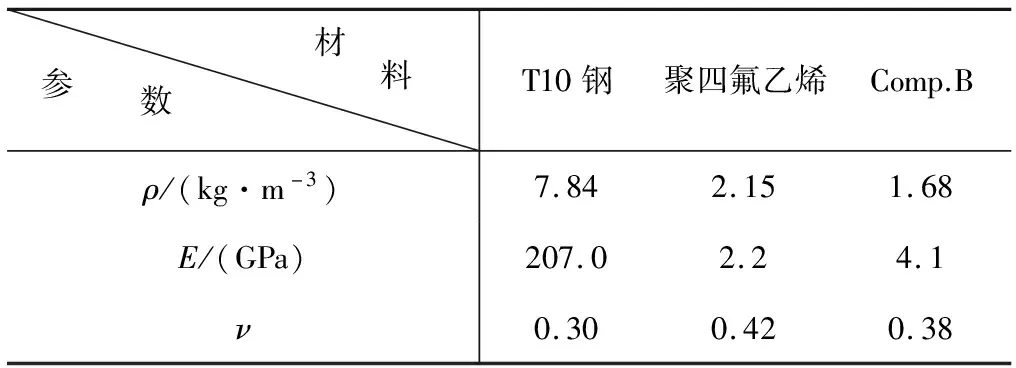
表1 材料的物性參數

4 結果與討論

對落高為1000 mm不同沖擊載荷沖擊作用下藥柱的應力進行分析以了解藥柱的動態力學性能響應的基本情況。圖3所示為落錘質量為40 kg，落高為1000 mm藥柱的應力云圖。由圖3可見，藥柱撞擊面邊緣和撞擊面附近的側面圓周上應力分布不均勻，且最大應力和最小應力在這些區域內間隔分布。圖4所示為落槌質量為400 kg，落高為1000 mm藥柱的應力云圖。和圖3相比較而言，圖4所示藥柱中的應力分布較為均勻，且最大應力出現在藥柱撞擊面邊緣和撞擊面附近的側面圓周上，應力沿徑向從撞擊面邊緣到撞擊面中心逐漸減小，沿軸向從撞擊面附件的圓周到藥柱底部逐漸減小。

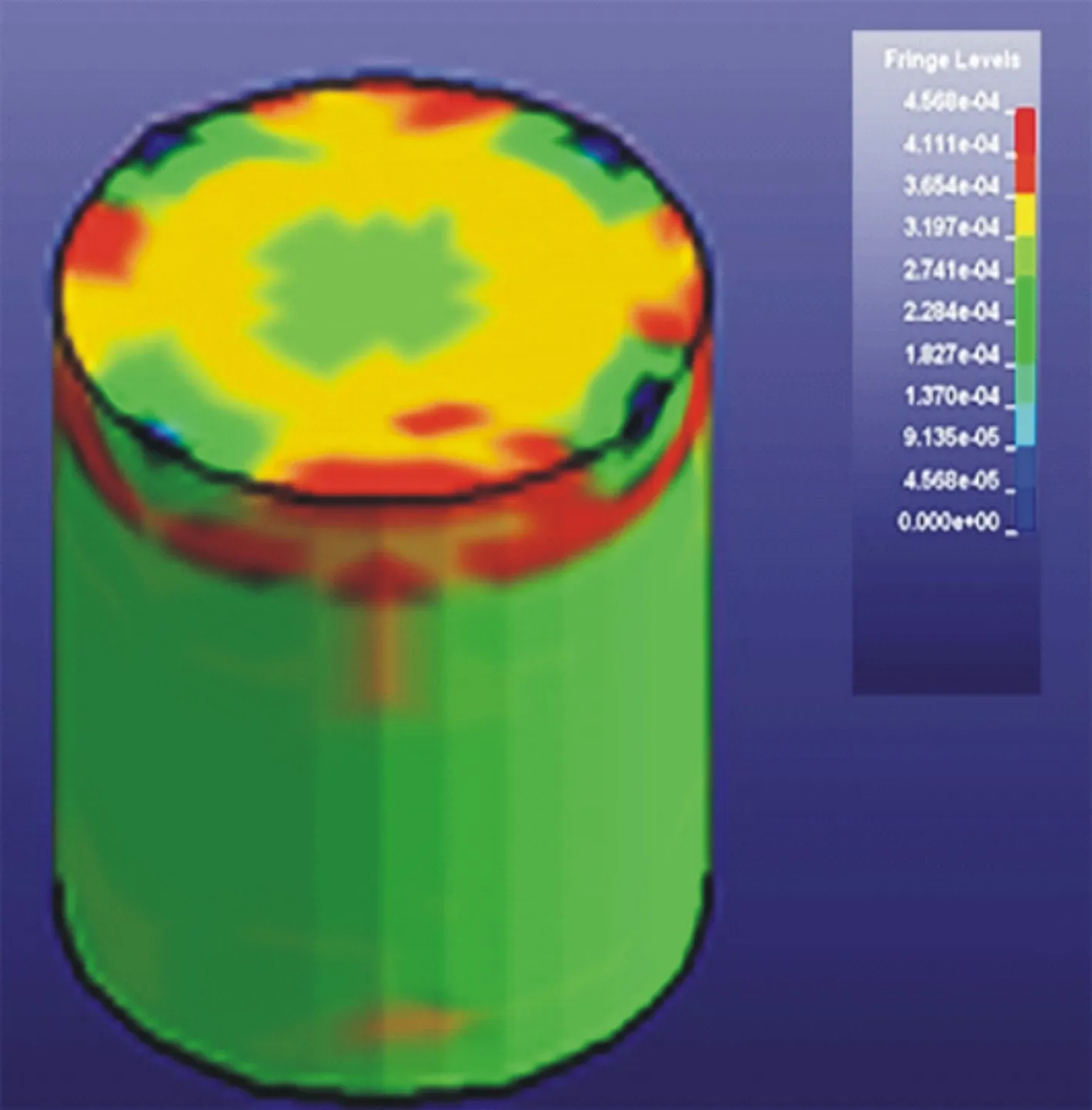
圖3 落錘質量為40 kg，落高為1000 mm藥柱的應力云圖

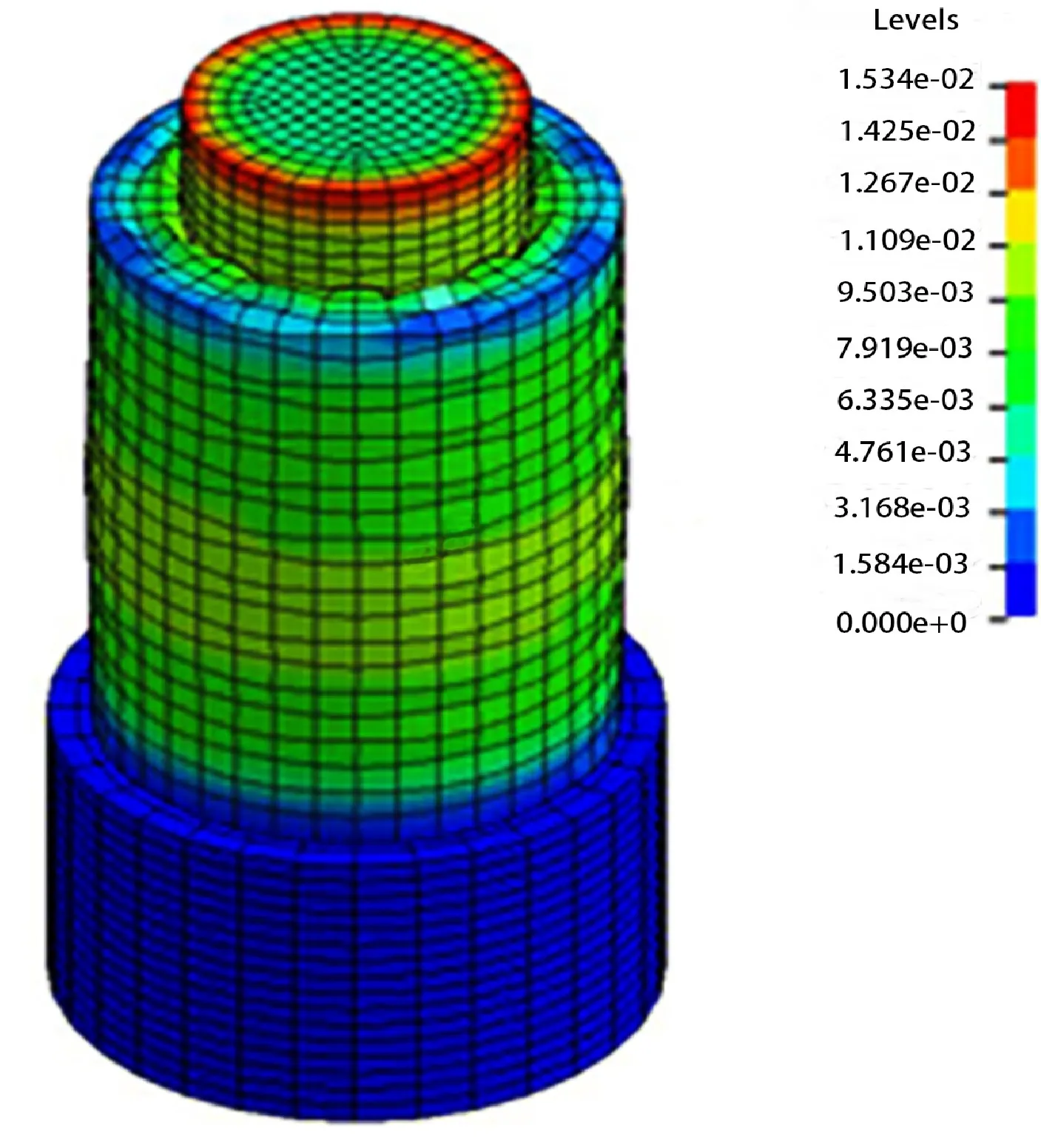
圖4 落錘質量為400 kg，落高為1000 mm藥柱的應力云圖

圖5所示為落錘質量為40 kg，落高為1000 mm，數值模擬的有效應力隨時間的變化關系曲線。由圖5可見，隨著時間的增加，應力先增大，當時間為0.5 ms時，應力達到最大值41.0 MPa。此后，隨著時間的增加應力開始下降，并在1.2 ms時達到最小值12.5 MPa。隨著時間繼續增加，應力繼續增大并在1.5 ms時達到穩定值 25.0 MPa，此后，應力基本保持恒定，不再隨時間發生變化。藥柱的應力-時間曲線左端波形近似為一個周期的正弦函數曲線，其二階導數為藥柱的加速度方程，其形式仍為一元正弦函數，符號與圖5中的曲線相反。

圖6所示為落錘質量為40 kg，落高為1500 mm，數值模擬的有效應力隨時間的變化關系曲線。由圖6可見，落錘質量相同，落高不同時，藥柱的應力變化趨勢與圖5的類似：應力先增大后減小；達到最小值后開始增大并隨后趨于穩定。由圖6可知，藥柱的應力最大值為80.0 MPa，最小值為6.0 MPa，應力加載達到最大值的時間為0.7 ms，應力值為最小時對應的時間為1.3 ms。此后，隨著時間的增加，應力增大，并在1.5 ms時達到穩定值50.0 MPa，此后，應力值基本不隨時間的增加發生改變。

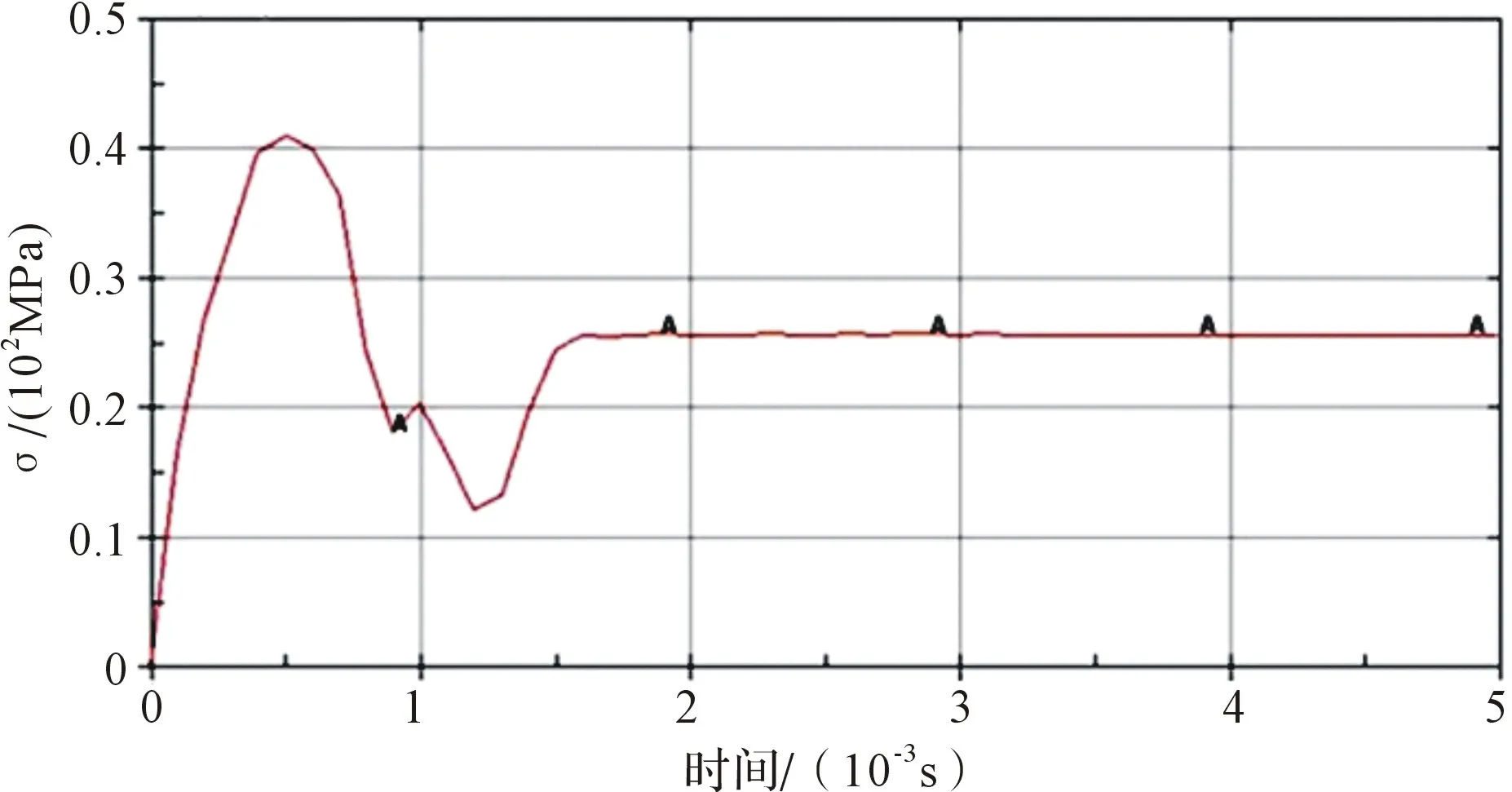
圖5 落錘質量為40 kg，落高為1000 mm沖擊作用下應力-時間曲線

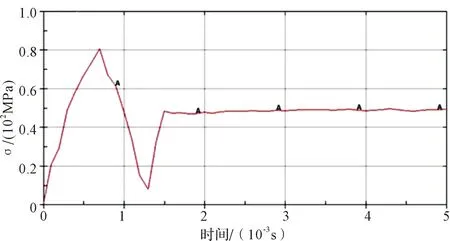
圖6 落錘質量為40 kg，落高為1500 mm沖擊作用下應力-時間曲線

為了分析不同沖擊載荷下的應力變化規律，落錘質量選定為400 kg，在落高分別為1000 mm和1500 mm條件下下對藥柱的應力隨時間的變化關系進行仿真計算，所得的應力-時間關系曲線分別如圖7和圖8所示。

由圖7可知，當落錘質量為400 kg，落高為1000 mm時，應力波動比較劇烈。隨著時間的增加，應力曲線有三個明顯的應力上升和下降的階段。第一階段的應力上升時間為1.1 ms，應力峰值為90.0 MPa，隨后隨著時間的增加，應力值開始下降，在時間為1.4 ms時，應力值降為5.0 MPa。而后隨著時間的增加，應力響應開始進入第二個上升階段，且應力增大的速率明顯快于第一階段。在時間為1.85 ms時，應力達到第二個峰值，其大小為150.0 MPa。此后，應力快速下降，在0.15 ms內降為0 MPa后進入應力上升的第三階段。在第三階段應力上升速率先快后慢，并在時間為4.0 ms時達到峰值180.0 MPa，隨著時間的繼續增加，應力開始下降，且下降的速率逐漸增大。

由圖8可知，當落錘質量為400 kg，落高為1500 mm時，應力隨時間的變化關系曲線仍有三個上升和下降階段，第二個階段變得不明顯。和圖7相比較而言，圖8的應力-時間曲線應力波動范圍大，但應力隨時間的變化沒有圖7中曲線波動劇烈。由圖8可見，第一階段的應力上升時間為0.7 ms，應力峰值為100.0 MPa，隨后隨著時間的增加，應力值開始快速下降，在時間為0.75 ms時，應力值降為0 MPa。而后隨著時間的增加，應力響應開始進入第二個上升階段，且應力增大的速率明顯慢于第一階段。在時間為1.1 ms時，應力達到第二個峰值，其大小為30.0 MPa。此后，應力快速下降，在0.1 ms內再次降為0 MPa進入應力上升的第三階段。在該階段應力上升速率先快后慢，并在時間為3.0 ms時達到峰值225.0 MPa，隨著時間的繼續增加，應力開始下降，且下降的速率逐漸增大。

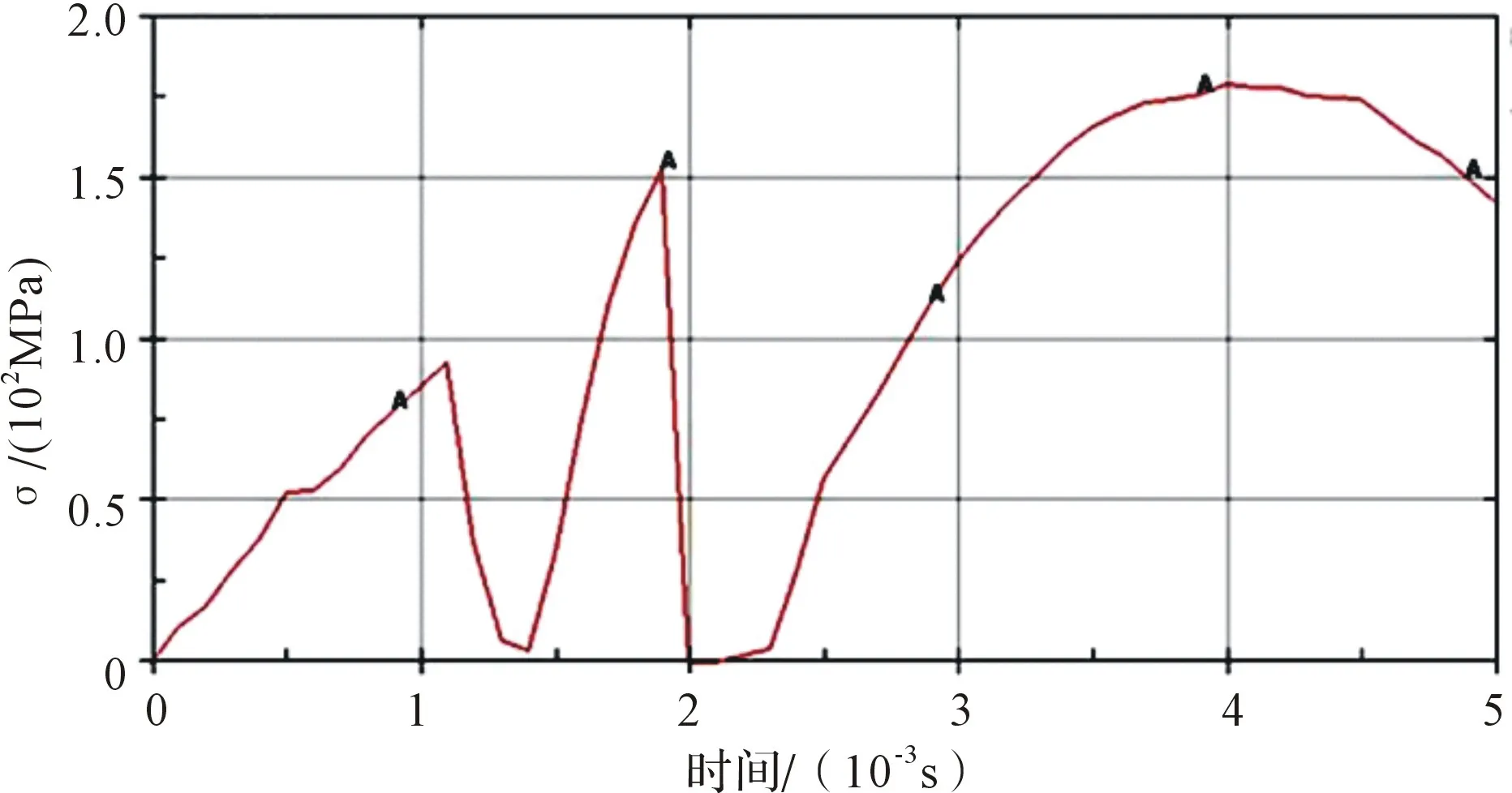
圖7 落錘質量為400 kg，落高為1000 mm沖擊作用下應力-時間曲線

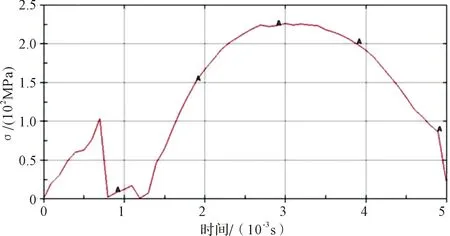
圖8 落錘質量為400 kg，落高為1500 mm沖擊作用下應力-時間曲線

綜合圖7和圖8可知，和落錘質量為40 kg的情形不同，落錘質量為400 kg時，落高增大，藥柱應力達到峰值的時間縮短。

5 結論

基于實驗結果擬合的應變率相關Johnson-Cook本構模型，利用LS-DYNA非線性有限元軟件對含能材料Comp.B炸藥的落錘沖擊特性進行分析。模擬選定的條件為：落錘質量為40 kg和400 kg。落高為1000 mm和1500 mm。通過模擬分析得出如下結論：

(1)當落錘質量為40 kg而落高不同時，應力-時間曲線的變化趨勢相同：隨著時間的增加應力先增大后減小，再增大直至維持穩定。不同之處在于：落高增大，應力波動范圍變大；落高增大；應力增大到最大值所需的時間增加；落高增大，應力-時間曲線的峰變尖銳。

(2)當落錘質量為400 kg而落高不同時，應力-時間曲線的變化趨勢也相同：隨著時間的增加應力先后經歷三個先增大后減小的過程。不同之處在于：落高增大，應力波動范圍變大；落高增大；應力增大到最大值所需的時間減少；落高增大，應力-時間曲線第二階段的增大減小過程變得不明顯。

(3)落錘質量相同落高不同時，應力-時間關系曲線變化趨勢相似；落高相同落錘質量不同時，應力-時間關系曲線變化趨勢不同。