基于灰色神經網絡在新零售目標產品預測中的研究

汪 想，龔誼承，程明輝，曾慶蓉

（1.武漢科技大學汽車與交通工程學院，湖北 武漢 430065；2.武漢科技大學理學院，湖北 武漢 430065）

隨著中國經濟的不斷發展，人們對目標產品的需求發生了顯著變化。性價比不再是人們的唯一訴求，人們更加愿意關注個性化、時尚化及美觀化，并將其作為對目標產品的重要需求。

同時，隨著新零售行業的不斷發展，新零售產品的種類呈爆發式增長，新零售產品類別不斷細化。這也導致商家對目標產品的分類管理十分困難。如何根據層次復雜、種類繁多的歷史數據，對目標產品的需求進行精準預測，成為目前絕大部分零售商家關注的主要問題。

本文首先通過逐步回歸分析篩選出影響目標產品銷量的主要因素，接著通過灰色神經網絡對目標產品的銷量進行預測。由于灰色神經網絡的初始權值與閾值隨機選擇，導致網絡在學習與進化過程中較容易陷入局部最優解。故引入遺傳算法對灰色神經網絡進行優化，以提高模型預測的準確度。

1 研究方法

1.1 逐步回歸理論

逐步回歸理論（Stepwise Regression Theory）是運用回歸原理并進行雙檢驗的一種理論。從本質上來說，逐步回歸是從一組候選變量中構建回歸模型，并識別出顯著變量的過程。

具體按如下3 步展開：①引入變量。對未引進變量進行F 檢驗，若顯著則引進。②剔除變量。對引進的自變量進行F 檢驗，若不顯著則剔除。③重復步驟①及步驟②，直至既沒有顯著的變量選入方程，也沒有不顯著的變量從方程中剔除為止，保證最后所篩選出的變量集達到最優。

1.2 灰色系統理論

灰色系統理論（Grey System Theory）是一種研究貧信息、小樣本、不確定性問題的一種理論。從本質上來說，主要是依據對少量確定信息的開發與提取，獲取有效信息，并以此為基礎達到對系統運行行為、演化過程的明確描述與有效監控。

1.3 灰色神經網絡

灰色神經網絡（Gray Neural Network）是一種基于灰色理論構建的神經網絡，適用于不確定系統行為特征值發展變化的預測。通過灰色神經網絡將初始樣本分為5 部分：標簽價、銷售價、折扣、庫存量、銷售特征，然后綜合這些因素對銷量進行預測。

對初始樣本中的skc 進行分類以及合并，選取累計銷售額前10 的skc 作為目標skc。將得到的目標skc 和日期代入模型，具體模型如下：

涉及n個參數的灰色神經網絡模型的微分方程表達式為：

式（1）中：y1為系統輸出參數；a，b1，b2，…，bn-1為微分方程系數；y1，y2，…，yn為系統輸入參數。

式（1）的時間響應式為：

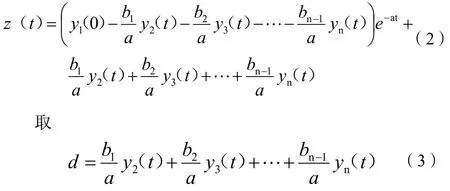
式（2）可作如下轉化：

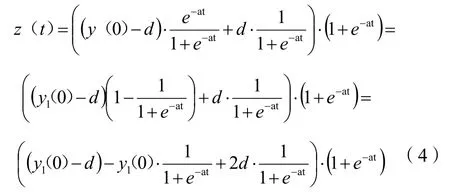
將變換后的式（4）映射到一個拓展的BP 神經網絡中就得到了n個輸入參數，1 個輸出參數的灰色神經網絡，網絡拓撲結構如圖1 所示。

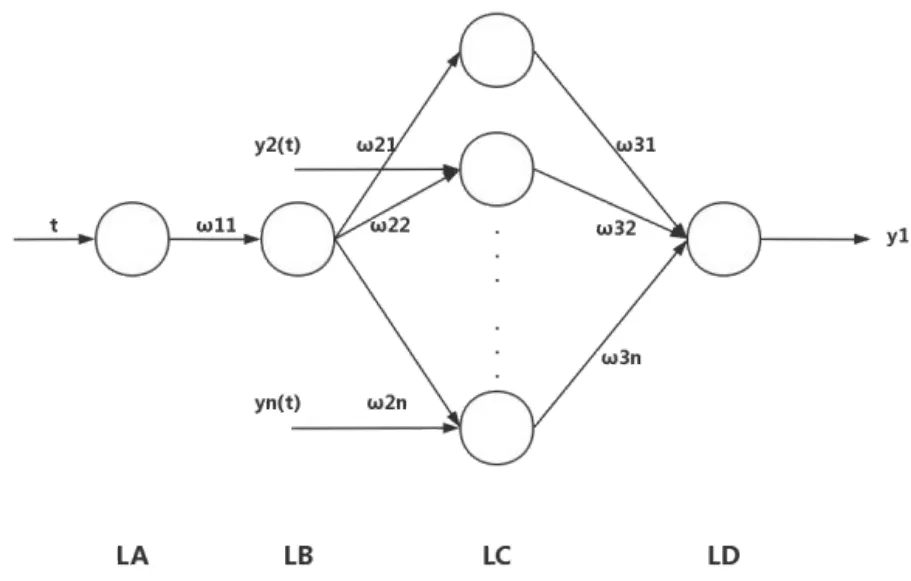
圖1 灰色神經網絡拓撲結構圖

1.4 遺傳算法

遺傳算法（Genetic Algorithms）是一種隨機搜索最優化方法。它將自然界生物進化的原理結合優化參數形成的編碼串聯群體。按照所選擇的適應度函數，通過選擇、交叉和變異操作對個體進行篩選。使適應度值好的個體被保留，適應度差的個體被淘汰。這樣反復循環，直至滿足條件。具體按如下5 步展開：①種群初始化，并對個體進行評價。②選擇操作。從舊群體中，以一定概率選擇個體到新群體中，個體適應度值越好，對應的概率越大。③交叉操作。從群體中任選兩個個體，隨機交換一點或多點染色體。④變異操作。從群體中任選個體，選擇染色體中的一點進行變異以產生適應度值更好的個體。⑤終止條件判斷。滿足則結束，否則返回步驟②。

2 本文的分析思路與框架

基于灰色系統理論（GST）、灰色神經網絡（GNN）、遺傳算法（GA）的理論基礎，本文具體做了如下6 步工作：①對原始數據進行預處理。包括對異常值N/A 和空值的剔除、對skc 的銷售數據進行分類及整合、篩選出累計銷量前10 的skc 作為目標skc、對目標skc 相關銷售數據進行標準化處理。②確定灰色神經網絡結構。根據逐步回歸分析確定輸入數據為5 維，輸出為1 維，所以灰色神經網絡結構為1—1—6—1，即LA 層有1 個節點，輸入為時間序列，LB 層有1 個節點，LC 層有6 個節點，第2～6 個分別輸入標簽價、銷售價、折扣、庫存量、銷售特征的5 個因素的歸一化數據，輸出為預測銷量。③按照5∶1 的比例劃分訓練集與測試集。④運用遺傳算法優化灰色神經網絡，確定最優的初始權值與閾值。⑤基于訓練集和測試集對灰色神經網絡進行訓練，直至滿足條件。⑥利用訓練好的灰色神經網絡對目標skc 的銷量進行預測，并對預測結果的誤差進行檢驗。

3 數據概述及預處理

本文所使用的數據集來自MathorCup 官網賽題（http://www.mathorcup.org/detail/2294）。包含了某新零售公司于2018—2019 年留存的16 539 種skc 的相關銷售數據，共6 個變量（前5 個為特征變量，最后一個“tiny_class_code”為標簽變量）。

為了方便后續的機器學習，對原始數據進行如下3 步預處理：①對原始數據進行篩除。檢測出原始數據中存在的異常值N/A 及空值，并進行剔除。②選取目標skc。篩選出2018—2019 年累計銷量前10 的skc 作為目標skc，并對目標skc的相關銷售數據進行分類與整合，同時將各目標skc 所對應的產品年份（year_id）作為目標skc 的銷售特征。③數據標準化處理。為消除量綱的影響，對提取的目標skc 相關數據進行Z 標準化處理，如式（5）所示。

式（5）中：u為所有目標skc 的均值；σ為所有目標skc 的標準差。

4 灰色神經網絡求解結果

4.1 灰色神經網絡的構建

首先建立多元線性回歸模型，對自變量X1，X2，…，X6與因變量Y進行多元線性回歸：

式（6）中：Y為目標skc 的銷量；X1，X2，…，X6為影響因素（標簽價、銷售價、折扣、庫存量、小類編碼、銷售特征）；ε為誤差項。

由于建立回歸模型時，并不是每一個因素對Y的影響程度都很大。我們應用逐步回歸分析法對因素進行篩選。利用MATLAB 從目標skc 中隨機抽取了36 個樣本。然后利用這36 個樣本的指標值通過SPSS 軟件進行求解，得到相關因素對目標skc 銷量的五元線性回歸方程。如式（7）所示。

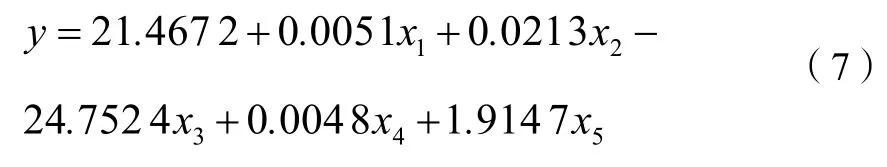
其中最后篩選和剔除后剩下的影響因素為：標簽價x1、銷售價x2、折扣x3、庫存量x4以及銷售特征x5。

為表明選取的影響因素與目標skc 的銷量具有顯著聯系。本文利用MATLAB 對五元線性回歸方程進行顯著性檢驗。結果如表1 所示。

由表1 可得：相關系數R2=0.903 192 107 016 042，說明五元線性回歸方程十分顯著，F值對應的概率P＜α，拒絕H0，根據F檢驗，五元線性回歸模型成立。

表1 統計檢驗表

4.2 灰色神經網絡求解

由于灰色神經網絡的初始權值與閾值隨機選取，在網絡學習進化時很容易陷入局部最優解，會對預測精確度產生較大影響。

本文決定采用遺傳算法對灰色神經網絡進行優化，即利用遺傳算法來優化a、b1、b2、b3、b4、b5這6 個參數。

遺傳算法對目標skc 的樣本個體進行實數編碼，將個體對應的灰色神經網絡預測誤差作為個體適應度值。經過不斷調試，設置種群規模為25，迭代次數為100。遺傳算法優化得到的最佳初始參數值如表2 所示。

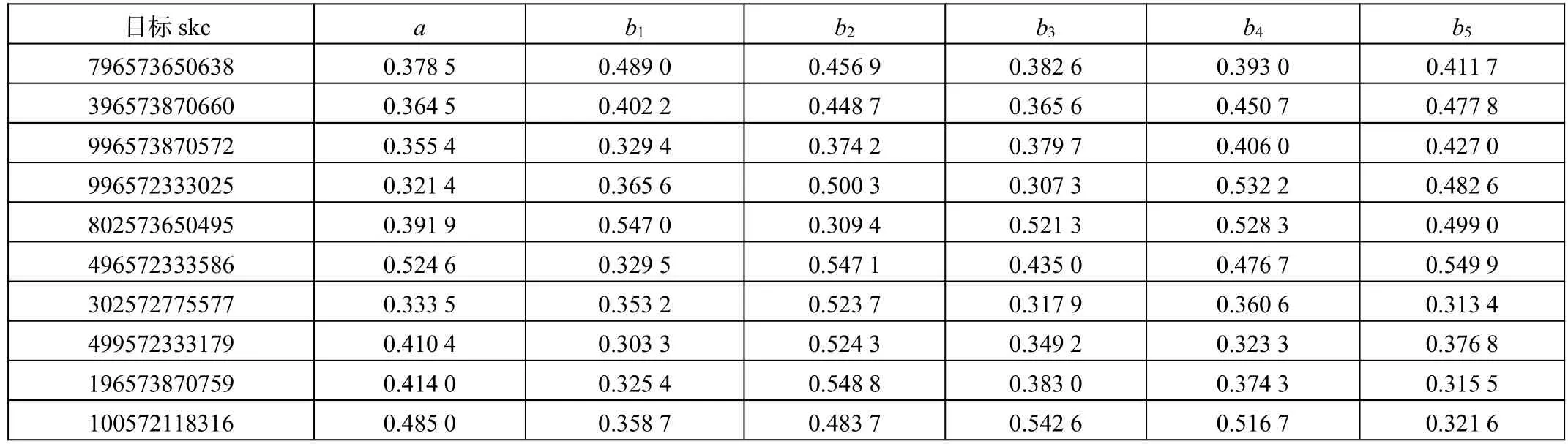
表2 目標skc 最佳初始參數值

將最佳初始參數值賦給灰色神經網絡，利用遺傳算法優化的灰色神經網絡模型對目標skc 的銷量進行預測。首先取前30 周的數據作為訓練集訓練網絡，網絡學習共100 次，然后用后6 周的數據評價網絡的預測性能。將得到的預測值與真實值以折線圖的形式進行對比，并對預測值的誤差進行檢驗。結果如圖2 所示。

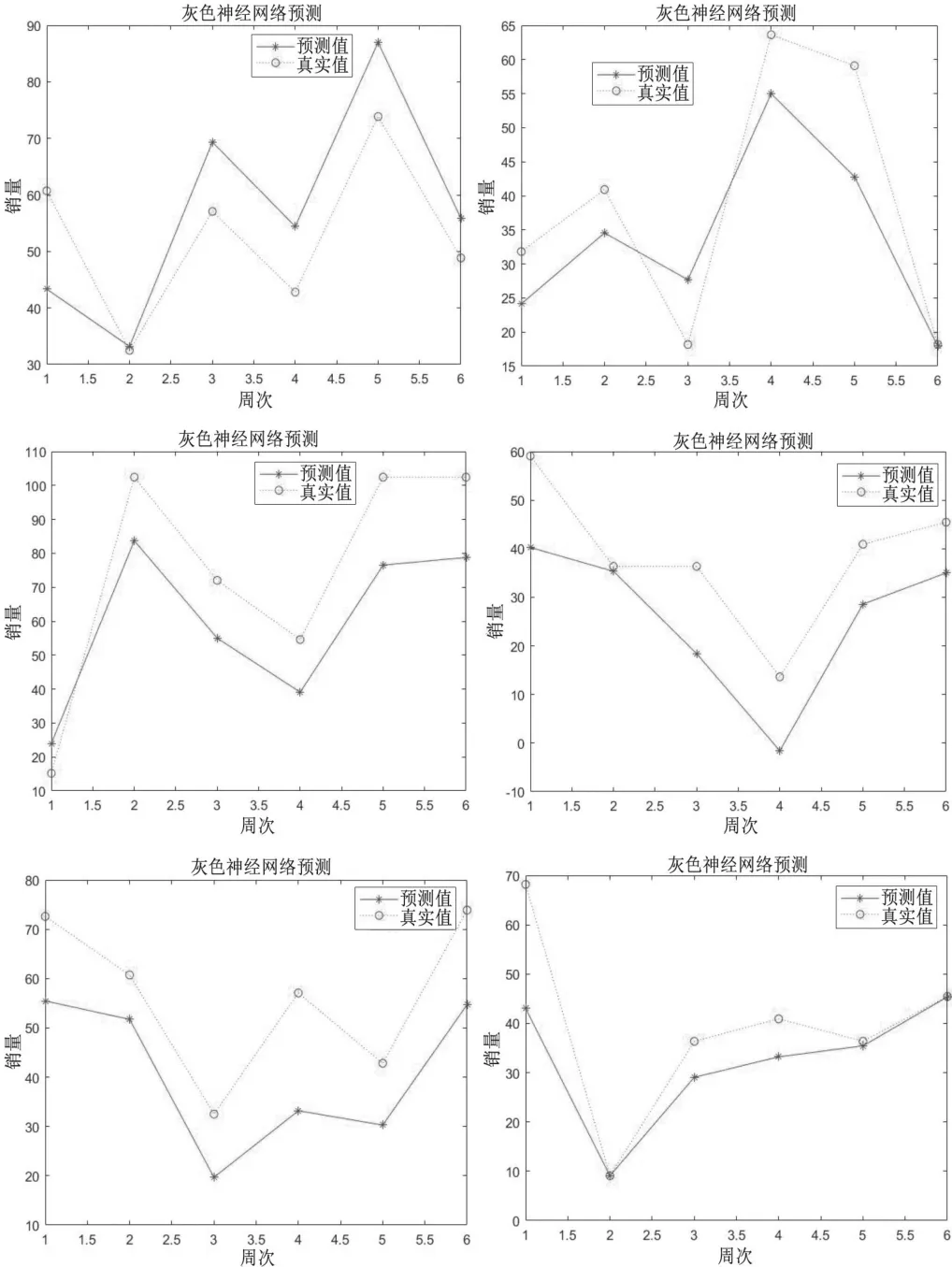
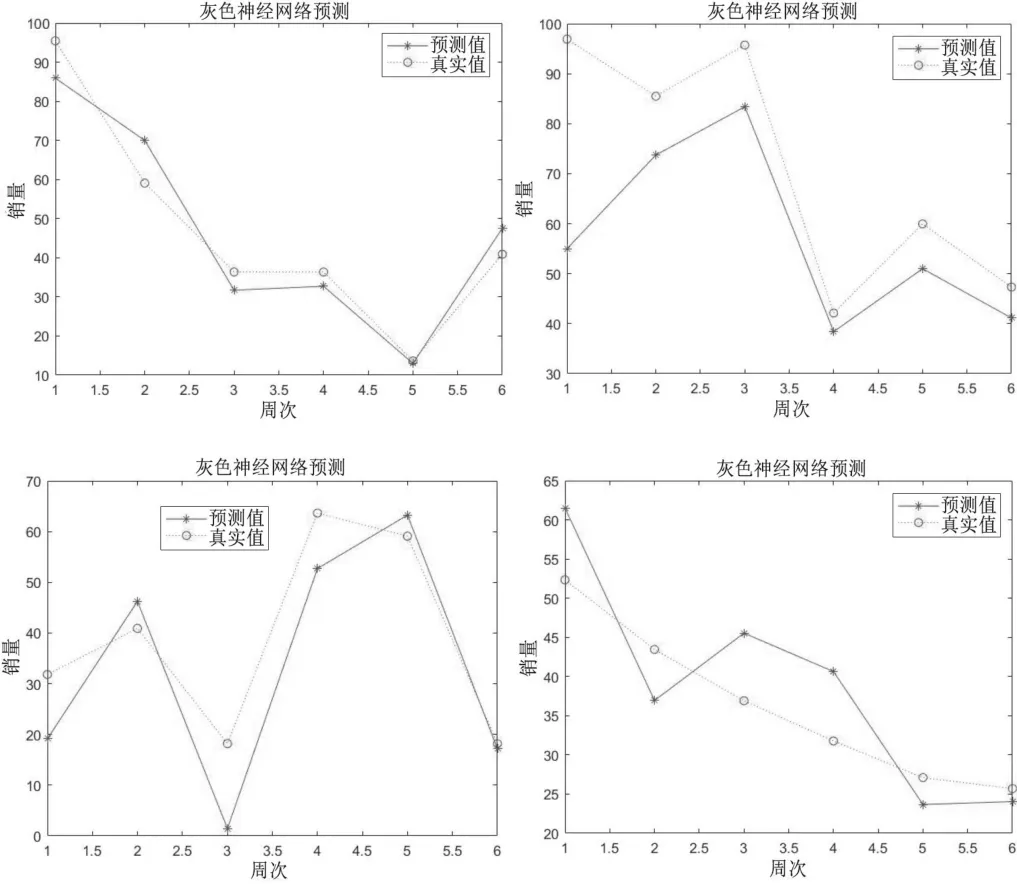
圖2 目標skc 預測結果

4.3 灰色神經誤差分析

為了證明模型預測的準確度，本文對灰色神經網絡模型的預測誤差進行R2檢驗。結果如表3 所示。

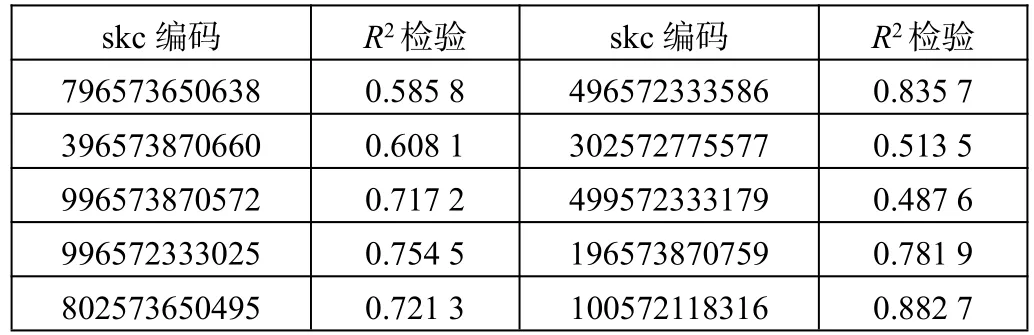
表3 R2 誤差檢驗表

從表3 中可看出，R2的值基本處于0.5～1 之間。故該灰色神經網絡模型的擬合優度非常優異，模型的預測結果十分準確。

5 結語

針對新零售行業目標產品需求的精確預測。首先，本文構建了基于逐步回歸的多元線性回歸模型，用于目標產品銷量影響因素的篩選及分析，得到影響目標產品銷量的因素有標簽價、銷售價、折扣、庫存量、銷售特征。其次，本文基于灰色系統理論構建了灰色神經網絡，用于目標產品銷量的預測，由于灰色神經網絡的初始權值與閾值隨機選取，在網絡學習進化時很容易陷入局部最優解，會對預測精確度產生較大影響，故本文采用遺傳算法對灰色神經網絡進行優化。最終依據誤差檢驗結果，該模型所得目標產品銷量的預測值與真實值之間的誤差非常微小，預測誤差在0.05～0.1 之間，預測準確度較高。該模型十分適用于新零售行業目標產品需求的精確預測。