大跨度公鐵平層合建斜拉橋主梁有效寬度研究

李秀華,任萬敏,曹海靜

(1.中鐵二院工程集團有限責任公司,成都 610031； 2.中鐵西南科學研究院有限公司,成都 610031)

大跨度公鐵平層合建橋主梁常采用寬幅鋼箱梁截面形式，鋼箱梁具有抗彎能力強、抗扭剛度大、材料利用率高、造型優美等特點被廣泛應用于橋梁工程中[1]。箱梁在彎曲橫向力作用下，橫向力通過腹板傳遞給頂底板，由于頂底板剪切變形的不均勻性，遠離腹板的位置其縱向位移滯后于靠近腹板的位置，因此產生頂底板內彎曲法向應力的不均勻分布，稱為剪力滯效應[2]。對于寬幅鋼箱梁斜拉橋，主梁在彎矩、軸力的復合作用下，相比一般的簡支、連續梁體系更為復雜，箱梁翼緣的剪力滯效應尤為突出。若忽略剪力滯效應的影響，可能導致結構局部應力超限，甚至產生橋梁結構的整體破壞[3]。

目前，國內外規范對于鋼箱梁剪力滯效應并未統一，我國公路、鐵路的橋梁設計規范均僅適用于純彎構件，而斜拉橋由于拉索的作用，主梁為多點彈性支撐的壓彎構件，規范中的計算方法并不適用[4]。斜拉橋規模較大，結構復雜，拉索和支座縱向分布對主梁剪力滯有明顯影響和規律性，需要根據橋梁自身特點進行專門研究和設計。聶建國等研究了組合梁在軸向力作用下混凝土橋面板正應力分布情況及傳遞角度[5]。翟曉亮等提出了斜拉索水平軸向力作用下橋面板有效寬度系數沿跨長方向分布曲線計算公式，同時理論分析得出了彎矩作用下橋面板有效寬度系數的計算方法[6]。本文針對大跨公鐵平層合建斜拉橋多點連續彈性支撐且同時承受軸力和彎矩的特點，通過建立全橋空間有限元分析模型，研究拉索軸力和成橋荷載作用下寬幅箱梁的法向應力分布，總結提出了斜拉橋全橋有效寬度分布規律。總體來看，跨中區、塔梁交匯區、輔助墩區有效寬度下降趨勢明顯，與現有研究成果結論相近，設計時應重點關注此類區域，通過加厚板厚、加勁構造等方式優化結構設計。

大跨度公鐵平層合建橋具有跨度大、橋面寬、公鐵共同作用荷載重等特點，與相近跨度的斜拉橋相比，同等索距下寬幅箱梁的彎曲剪力滯特性更為突出。加之高速鐵路對結構剛度要求高，上行荷載較大，斜拉索索力隨之增大，由此帶來的拉索軸向力傳遞過程中，應力不均勻更為顯著。因此，有必要針對大跨公鐵平層合建斜拉橋主梁剪力滯效應開展深入研究。

1 項目概述

宜賓臨港長江大橋于宜賓市臨港區跨越長江，是新建川南城際鐵路與渝昆高鐵的過江通道，也是宜賓市規劃的過江通道。為節約通道資源和工程投資，采用“四線鐵路六車道公路”公鐵兩用橋梁方案。主橋按四線客運專線與六車道城市快速路同層設計，主橋梁長1 075.2 m，全橋孔跨可布置為9×40.7 m+(72.5+203+522+203+72.5) m+7×40.7 m，全橋立面布置見圖1。

圖1 全橋立面布置(單位：m)

主梁采用鋼箱梁，橋面布置四線，300 km/h高速鐵路設置在橋面中間，兩側各布置三車道設計速度80 km/h的城市主干道和人行道及非機動車道。橋寬63.9 m，采用國內首創公鐵平層設計，為目前世界寬度最大的公鐵兩用橋，主橋橋面布置及鋼箱梁斷面見圖2[7]。鋼箱梁采用單箱五室結構，流線型輪廓，梁高5.0 m，主梁總寬63.9 m，底寬34.45 m。橋面設2%人字橫坡，拉索錨固在鐵路和公路之間，采用內置式鋼錨箱，鋼梁標準節段長12 m，單側拉索采用2根索并置方案，拉索中心距0.9 m，順橋向索距12 m。橋面布置見圖2。

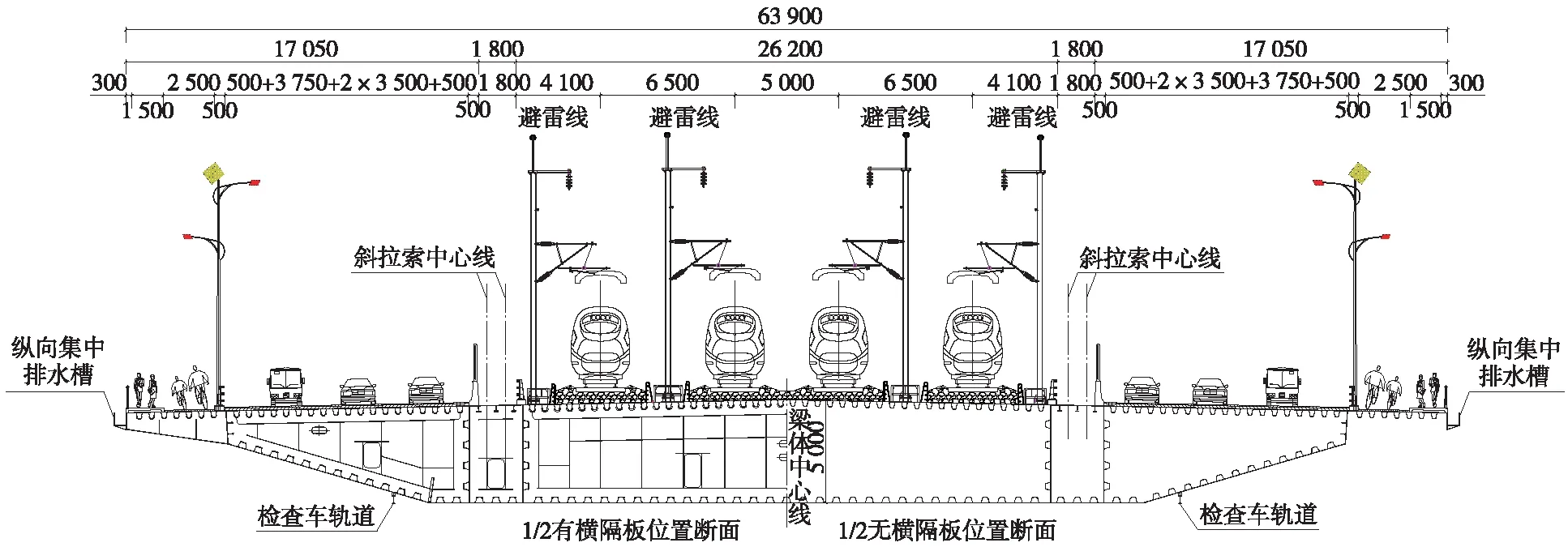
圖2 鋼箱梁橋面布置(單位：mm)

2 研究方法與模型建立

目前剪力滯效應的分析方法主要分為彈性力學解析法、比擬桿法、能量變分法[8]、有限元數值法和試驗研究法等。基于理論的分析方法往往需要對復雜結構進行簡化處理，對于鋼箱梁斜拉橋這種大型復雜結構體系，采用理論分析得到的結果與實際情況差異較大。隨著計算機技術的發展，基于板殼元的空間有限元方法成為了橋梁精細化分析的有效手段，通過建立全橋空間板殼單元模型，研究寬幅鋼箱梁斜拉橋的傳力路徑和受力行為，分析剪力滯效應和分布規律。

主橋采用有限元軟件Midas Civil建立空間有限元模型，主梁采用板單元模擬、主塔采用梁單元模擬、斜拉索采用桁架單元模擬，模型共有13 375個節點，24 768個單元。墩頂支座與主塔塔底采用一般支承模擬，塔梁間支座與索梁間采用彈性連接。全橋空間有限元模型如圖3所示，基于該模型開展剪力滯效應分析。

圖3 全橋空間有限元模型

采用該模型在成橋狀態下非線性靜力分析，研究恒載作用下鋼梁頂底板的應力分布，進而求得恒載作用下有效寬度，計算公式如式(1)所示，有效寬度系數如式(2)所示[9]。

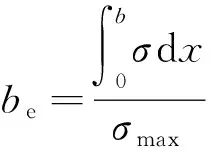
(1)

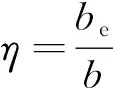
(2)

式中：be為鋼箱梁頂板有效寬度；b為箱梁頂板寬度；σ為箱梁頂板正應力；σmax為箱梁頂板最大正應力；η為頂板有效寬度系數。

3 縱向力作用下有效寬度系數

3.1 各國規范傳力規定

AASHTO LRFD規范[10]規定梁體在縱向集中力作用下，軸向力將沿兩側30°角方向傳遞，并逐漸均勻分布在整個橋面上，直至整個截面參與工作。German Deutsche Norm(DIN 1075)規范與之類似，角度為26.5°[11]。中國及歐洲國家等規范并未涉及軸向力作用下橋面有效寬度的問題。

3.2 拉索軸力作用下箱梁有效寬度

斜拉橋主梁為多點彈性支撐的壓彎構件，主梁成橋計算結果包含有恒載彎矩和拉索軸力的綜合影響，直接分析成橋結果很難分離拉索軸力影響結果。因此，國內外研究者常采用建立鋼梁節段模型，在節段端部施加集中荷載，分析節段各截面應力分布的方式查看軸力作用影響的情況，研究結論與現有規范結果較為接近。

對于斜拉橋，斜拉索連續作用于梁體，多根拉索作用下箱梁應力分布與單獨集中力效果不同。基于此，為研究斜拉索作用效果，可提取成橋狀態下錨固點索力值，通過拉索傾角換算縱向水平分力，將該分力以集中荷載方式作用于錨固點位置，計算箱梁頂板應力。根據應力不均勻情況，按式(1)、式(2)計算有效寬度系數，繪制成橋狀態(恒載)拉索軸力作用下全橋(半跨)有效寬度系數如圖4所示。

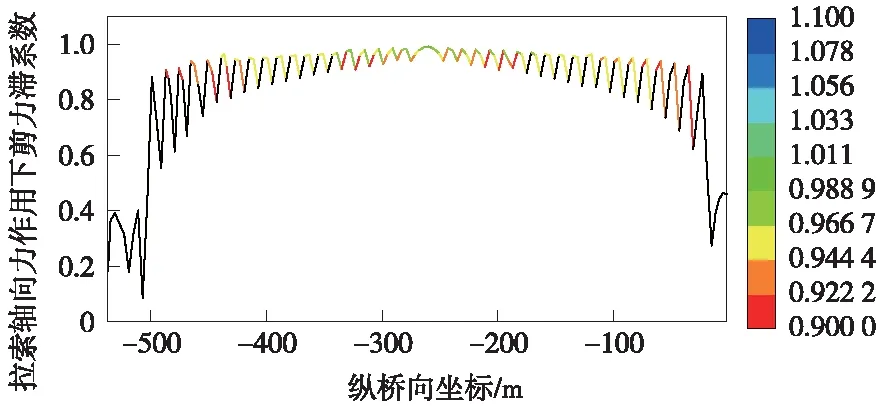
圖4 拉索縱向水平力作用下有效寬度系數分布

圖4中縱橋向坐標范圍為小里程側梁端至主跨跨中，坐標值為-537.6～0 m。從全橋有效寬度系數分布可以看出，受局部應力影響，最外側拉索作用點(坐標-520 m、-20 m)處縱向力作用下箱梁應力不均勻程度最高，有效寬度系數為0.1～0.3，隨著更多組拉索持續作用，應力擴散不斷積累，應力分布逐漸均勻，箱梁有效寬度系數逐漸增大并趨于平穩，主塔位置(坐標-261 m)處有效寬度系數為1。

4 成橋狀態主梁有效寬度

4.1 關鍵截面應力橫橋向分布

在成橋狀態下主梁受軸力、彎矩的共同作用，箱梁頂板縱向應力出現明顯的不均勻現象[12]。為計算頂板應力不均勻的變化規律，通過空間有限元模型成橋計算，確定主梁恒載、主力工況作用下關鍵截面鋼箱梁頂、底板縱向正應力沿橫橋向分布情況[13]，公鐵活載以車道面方式加載[14]。邊跨跨中箱梁頂(底)板縱向正應力分布見圖5、圖6，橋塔位置箱梁頂(底)板縱向正應力分布見圖7、圖8， 主跨跨中箱梁頂(底)板縱向正應力分布見圖9、圖10，輔助墩位置鋼箱梁頂(底)板縱向正應力分布見圖11、圖12。

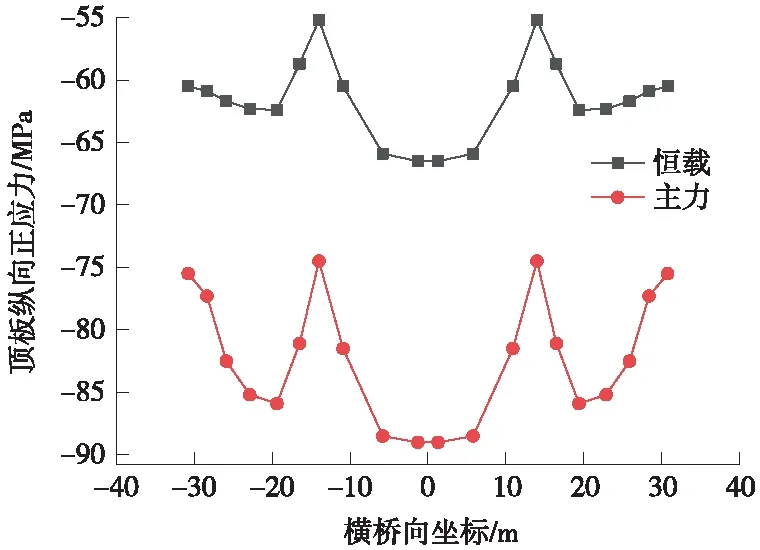
圖5 邊跨跨中箱梁頂板縱向正應力

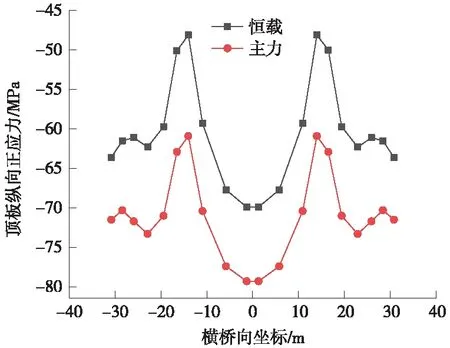
圖7 橋塔位置箱梁頂板縱向正應力

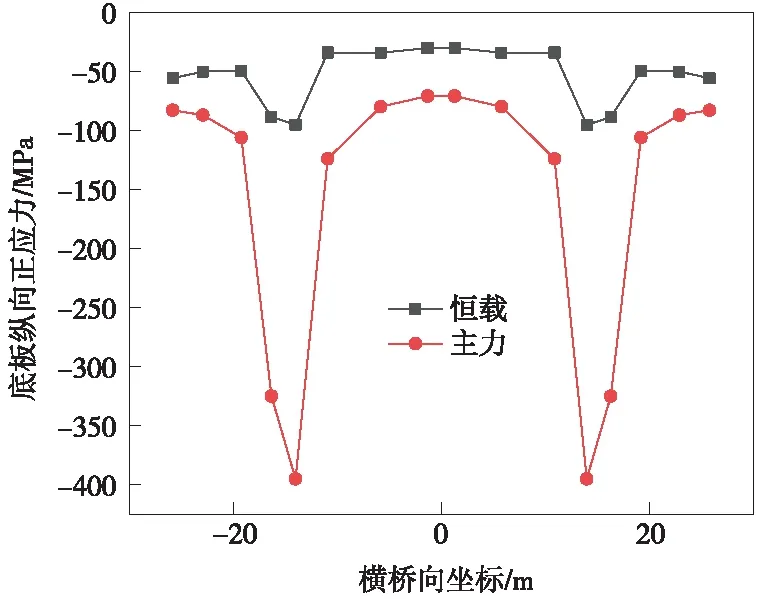
圖8 橋塔位置箱梁底板縱向正應力

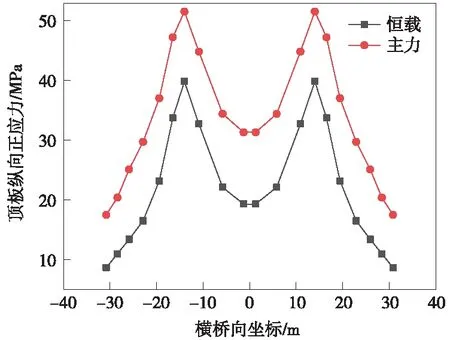
圖9 主跨跨中箱梁頂板縱向正應力

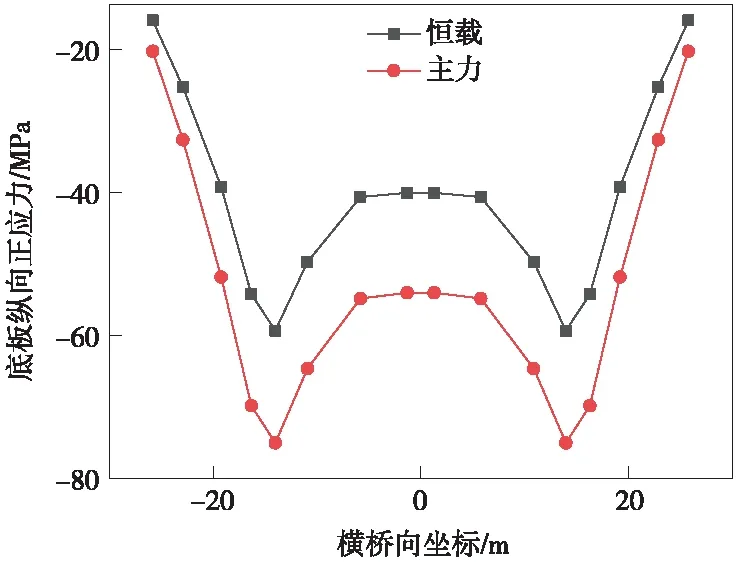
圖10 主跨跨中箱梁底板縱向正應力

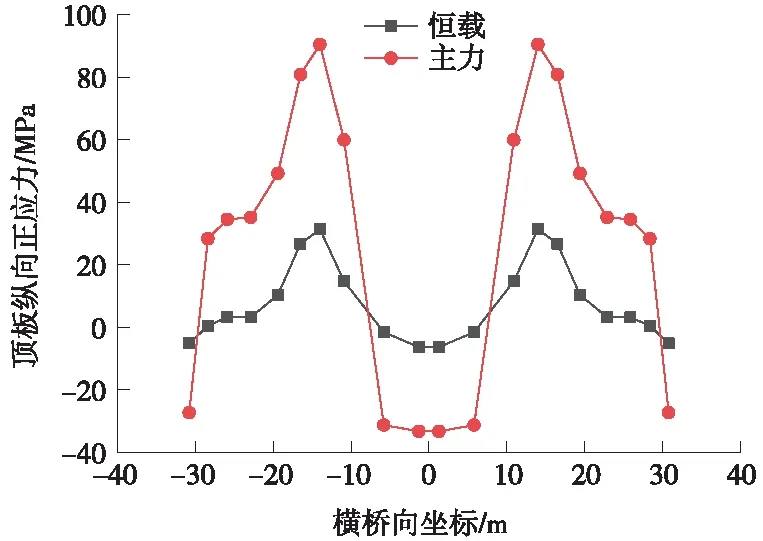
圖11 輔助墩位置鋼箱梁頂板縱向正應力

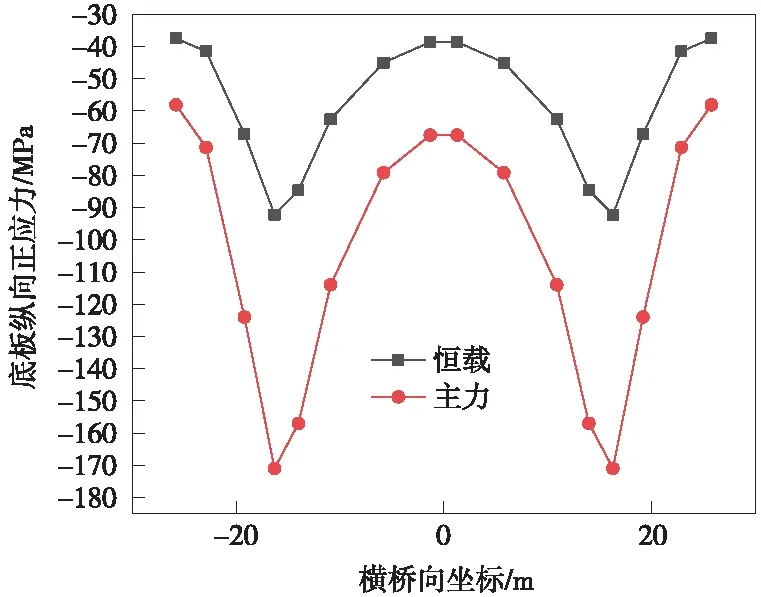
圖12 輔助墩位置鋼箱梁底板縱向正應力

根據圖5～圖12所示，鋼箱梁頂底板的縱向應力沿橫向分布應力相差不明顯，全橋典型位置處均呈現錨箱位置處應力較大，橫向跨中及兩翼應力較小的趨勢[15]。主力工況與恒載工況縱向應力的橫向分布變化趨勢一致。

由以上分析可知，邊跨跨中、橋塔位置頂板縱向為壓應力，主跨跨中頂板縱向應力為拉應力，輔助墩區域由于主梁負彎矩及拉索軸力的作用，呈現部分受拉，部分受壓的狀態，應力不均勻程度雖然較高，但應力水平滿足規范要求。無論頂板內縱向應力為拉壓狀態，在橫向分布均呈現拉索作用位置附近較大的趨勢，可知寬幅鋼箱梁縱向主要經由拉索錨箱及縱腹板傳力[16-17]。全橋底板縱向為壓應力，橋塔底板應力出現應力集中，因為該處為支座位置的緣故，因本模型未考慮支座位置處加勁加強處理[18]，故該處應力超限不反映真實情況，應由支座位置局部分析確定。

本橋邊跨跨中、橋塔、主跨跨中等位置處頂板應力主力與恒載工況之比為1.1～1.3，而輔助墩位置主力與恒載比值達到2.89，輔助墩位置活載作用占比明顯，且應力相對其他區域較大。因此，應著重考慮輔助墩區域頂板設計。

對于底板，邊跨跨中主力與恒載應力整體應力水平相差較大，最大應力比值為92/52.8=1.74。輔助墩位置處最大應力比值為171/92.2=1.85，輔助墩區域應力相對集中于支座位置處。成橋狀態下底板應力水平沿全橋(除支座附近外)基本一致，均在40～60 MPa以內，支座位置處應力水平較大，因此應根據應力分布合理確定底板板厚及分布。

4.2 鋼箱梁頂底板有效寬度

根據應力不均勻情況，按式(1)、式(2)計算有效寬度系數，繪制半個橋跨(對稱)的頂底板有效寬度系數如圖13、圖14所示。

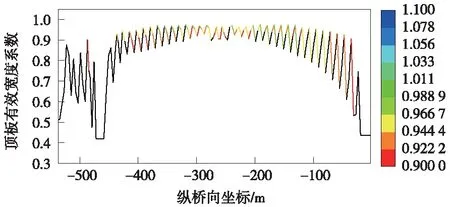
圖13 主梁頂板有效寬度系數全橋分布

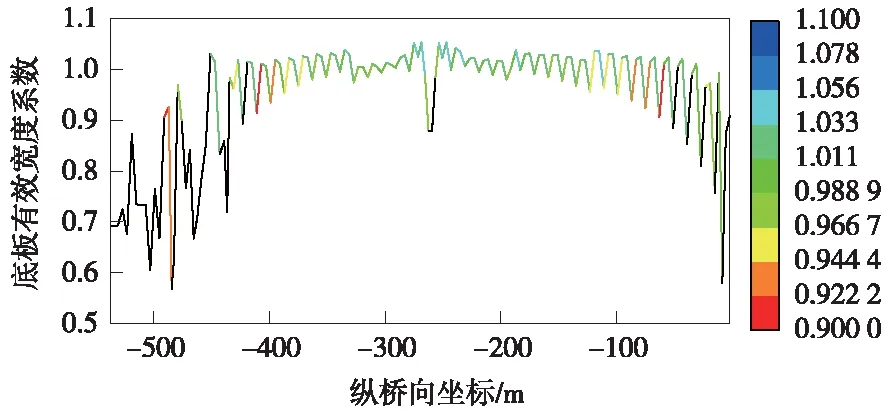
圖14 主梁底板有效寬度系數全橋分布

從圖13、圖14分析可知，頂板有效寬度系數最小為輔助墩頂處，其值為0.43，說明該截面處剪力滯效應最嚴重。索塔支座附近的剪力滯效應次之[19]。跨中附近的剪力滯效應較前兩者小，其有效寬度比為0.5。其余幾處斷面的剪力滯效應最小，有效寬度比基本在0.92左右，總結原因為彎矩作用下主跨跨中有效寬度系數最大，且在較長區域內均勻分布。軸力作用下主跨跨中有索區段內有效寬度系數沿跨長方向呈線性變化，有索區越靠近邊索有效寬度系數越小。底板有效寬度分布與頂板情況類似，由于橋塔支座局部應力集中等影響，橋塔位置處有效寬度折減更為明顯。以上規律符合斜拉橋鋼箱梁壓彎構件的受力特點[20]。相比拉索軸力作用成橋狀態下有效寬度系數受彎矩作用影響突出，主梁在塔梁交匯處、輔助墩墩頂位置處有效寬度系數明顯下降。

5 結論

以宜賓臨港長江大橋為例，研究大跨公鐵平層合建橋梁的主梁有效寬度分布規律，得到以下結論。

(1)大跨度公鐵平層合建橋因其橋面寬、公鐵共同作用荷載重等特點，同等索距下寬幅箱梁的彎曲剪力滯特性更為突出，拉索軸向力作用下應力不均勻更為顯著。

(2)斜拉索軸力作用下鋼箱梁有效寬度變化符合以下規律：外側拉索位置箱梁應力不均勻程度最高，隨著更多組拉索持續作用，應力擴散不斷積累，應力分布逐漸均勻，箱梁有效寬度系數逐漸增大并趨于平穩，橋塔位置處有效寬度最大。

(3)鋼箱梁頂底板的縱向應力沿橫向分布應力相差不明顯，全橋典型位置處均呈現錨箱位置處應力較大，橫向跨中及兩翼應力較小的趨勢。寬鋼箱梁縱向主要經由拉索錨箱及縱腹板傳力。輔助墩位置活載作用占比明顯，應力相對其他區域較大。

(4)頂板有效寬度比最小為輔助墩頂處，該截面處剪力滯效應最嚴重。索塔支座附近的剪力滯效應次之。跨中附近的剪力滯效應較前兩者小，其余幾處斷面的剪力滯效應最小，有效寬度比基本在0.92左右，符合斜拉橋鋼箱梁壓彎構件的受力特點。

(5)主梁在跨中區、塔梁交匯區、輔助墩區有效寬度下降明顯，設計時應重點關注此類區域，通過局部節段加厚板厚、優化加勁構造等方式滿足結構受力性能要求。