基于需量管理的工業園區混合儲能配置及運行優化研究

方濟城 楊俊杰 樊安潔 蔣 偉 邵凌峰

1(上海電力大學電子與信息工程學院 上海 200090) 2(國網江蘇電力有限公司經濟技術研究院 江蘇 南京 210000)

0 引 言

為應對全球能源緊缺和環境惡化問題，各國都在大力發展可再生能源發電技術并出臺太陽能等清潔能源的相關政策[1]。國家“十三五”規劃明確規定將繼續發展分布式光伏發電，鼓勵大型公共建筑及公共設施、工業園區等建設屋頂分布式光伏發電[2]。然而新能源的大規模應用也進一步影響著園區系統的供電穩定，為進一步提高供電可靠性，國家大力推動儲能的商業化應用[3]。

現普遍運用在用戶側的儲能設備多為蓄電池，能量密度較高。通過引導單類型蓄電池儲能(Single-type Battery Energy Storage,SBES)利用分時電價峰平谷的差異，“低儲高發”實現峰谷套利，改善整體電力系統的收益[4]。文獻[5]為工業用戶側儲能電池的商業推廣提供了初步的方案，評估用戶加裝儲能的經濟性并優化儲能配置。但考慮到工業園區負荷存在高頻功率波動的特點，電池受制于充放電周期、功率密度、成本等因素，并不能完全滿足園區系統需求。而以超級電容器(Super Capacitor,SC)為代表的功率型儲能可以彌補能量型儲能功率密度低的缺陷。因此本文應用能量型儲能鋰電池(Lithium Battery,Li-B)結合功率型儲能SC，形成HESS。HESS中的Li-B和SC可以形成能量響應幅度以及響應速率的互補，使得電力系統運行更加平穩，也減小了運行成本。

許多國內外學者圍繞HESS的應用問題展開深入探討。合理配置HESS需要對原始輸入數據進行高低頻功率分解，小波變換方法一直被廣泛應用，文獻[6-8]基于小波包分解技術，將風電功率分解為高頻分量和低頻分量，低頻分量并入電網，高頻分量由儲能裝置平抑。然而小波變換需要選擇合適的母小波，并且需要設置可行的分解層數，增加了高低頻的分解的不確定性。本文應用的經驗模態分解技術以原始數據為基礎的自適應分解，可以彌補小波變換的缺陷。HESS的應用多見于平抑新能源發電功率短時間尺度的波動，提高其電能質量。文獻[9-11]將風電功率分解為高頻分量、低頻分量和并網分量，高頻和低頻分量分別由SC和蓄電池補償，實現并網功率波動的平抑，并采用遺傳算法優化混合儲能系統容量配置。文獻[12-13]基于超級電容器和蓄電池組成的混合儲能系統，建立了短期動態控制模型，實現并網功率的平滑控制，并優化了儲能系統容量配置。從上述文獻可以看出，國內外研究HESS主要應用在風光發電側，而在工業用戶側配置方面的研究較少，優化過程單一。另外，在需量管理[5]以及兩部制電價計費模式的背景下，針對工業園區場景用戶負荷存在尖峰多、峰谷差大的特點，需要對其進行精細的運行優化研究，以進一步提升運行的經濟性。

基于目前研究的現狀，本文提出一種計及工業用戶用電需量的多時間尺度HESS容量配置和經濟運行模型。通過優化受電側混合儲能配置運行方法來降低工業園區用戶用電成本。以Li-B和超級電容器SC作為工業園區供電系統的HESS模塊，建立以HESS額定功率容量、最大需量為變量，需量收益、HESS全壽命周期、系統波動性為目標的兩階段月度和日前優化模型。模型中確定工業用戶上報的最大需量，引入峰谷差為評估約束，最大化用戶收益。應用改進的CPSO進行兩階段優化求解，將混沌映射加入常規粒子群算法，在算法后期保持了粒子多樣性。仿真結果表明，通過HESS替代SBES，能夠更好地實現削峰效果、平滑波形，且能大幅減少工業園區的電度電費和需量電費的繳納，進一步提升系統的經濟運行。

1 工業園區供電系統模型

針對工業園區負荷存在瞬時功率高、峰谷落差大的特點，本文引入SC與Li-B組成HESS，使電網系統平穩運行，進一步減少用電成本。

所設計的工業園區供電系統如圖1所示，該系統主要由新能源發電單元和混合儲能系統單元組成的光儲一體化系統以及工業用戶綜合負荷單元組成，通過能源管理中心對工業園區負荷進行控制調度。新能源發電單元包含就地安裝的光伏電池板，通過變換器連接母線。HESS單元主要包含Li-B以及SC。能量型儲能如Li-B用于平抑大幅值、小波動頻率的低頻分量；而功率型儲能如SC用于平抑小幅值、大波動頻率的高頻分量。光儲一體化結合工業用戶負荷一并與大電網相連，在兩部制電價機制下，HESS的充放電策略具體是：太陽能發電供給用戶有余電且電價較便宜時，考慮效益最大化，對HESS進行充電操作。而在電價較高時，對HESS進行放電操作，將多余的電能賣給電網。這種策略滿足了工業園區的負荷，又實現了清潔能源的高效利用。錯峰用電方式也減輕了電網的能源調度壓力，滿足了系統可靠運行要求，實現主網側與用電側的雙贏。

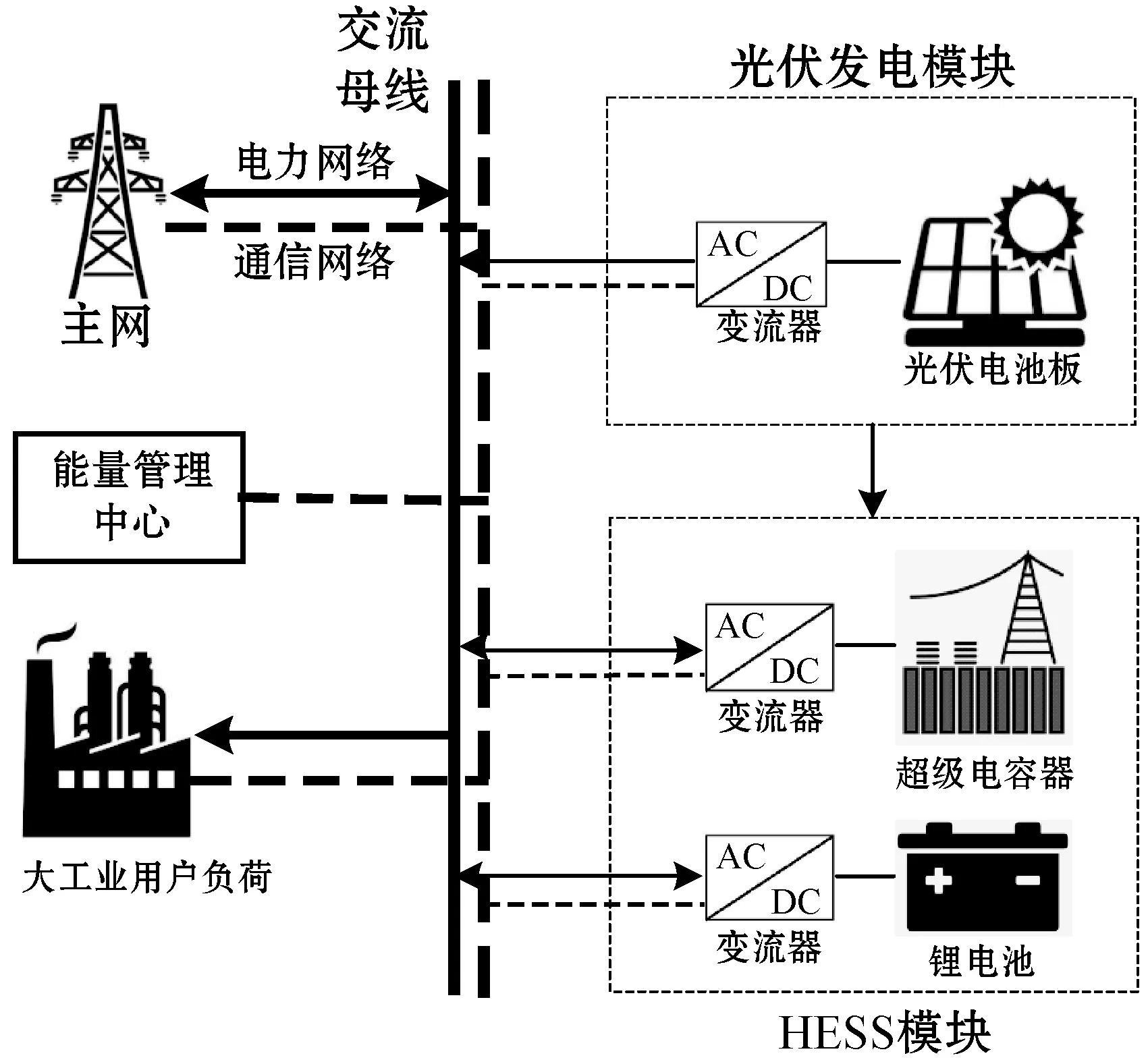
圖1 工業園區供電系統結構

將光伏輸出功率和用電負荷的等效值定義為凈負荷[14]，凈負荷PJ與負荷功率PL和光伏出力PPV的關系表示如下：

PJ=PL-PPV

(1)

對于多個隨機變量的處理，可應用蒙特卡洛模擬產生隨機值，將隨機量按照時序疊加，得到時段t內的凈負荷隨機量：

PJ(t)=[PL(t)+δL(t)]-[PPV+δPV(t)]

(2)

式中：δL(t)與δPV(t)分別為負荷和光伏出力的波動功率。

2 基于經驗模態分解(EMD)的混合儲能功率分配

本文通過應用EMD技術分解凈負荷功率信號來滿足HESS中超級電容和鋰電池不同平抑特性的要求，將多分量原始信號分解為固有模態函數(Intrinsic Mode Function,IMF)，不需要其他的先驗信息，是一種自適應的信號處理方法[15-16]。將單月的大工業用戶負荷與光伏模塊發電數據合成出的等效凈負荷曲線分解成一系列IMF分量。根據頻率混疊情況確定分頻頻率k，如圖2所示，可以在混疊區域最少的條件下分離高、低頻波動分量。具體公式如下：

(3)

式中：PL_bat與PL_cap表示分別提供給Li-B和SC平抑的低高頻波動分量；ci表示各階IMF分量；r為余量。

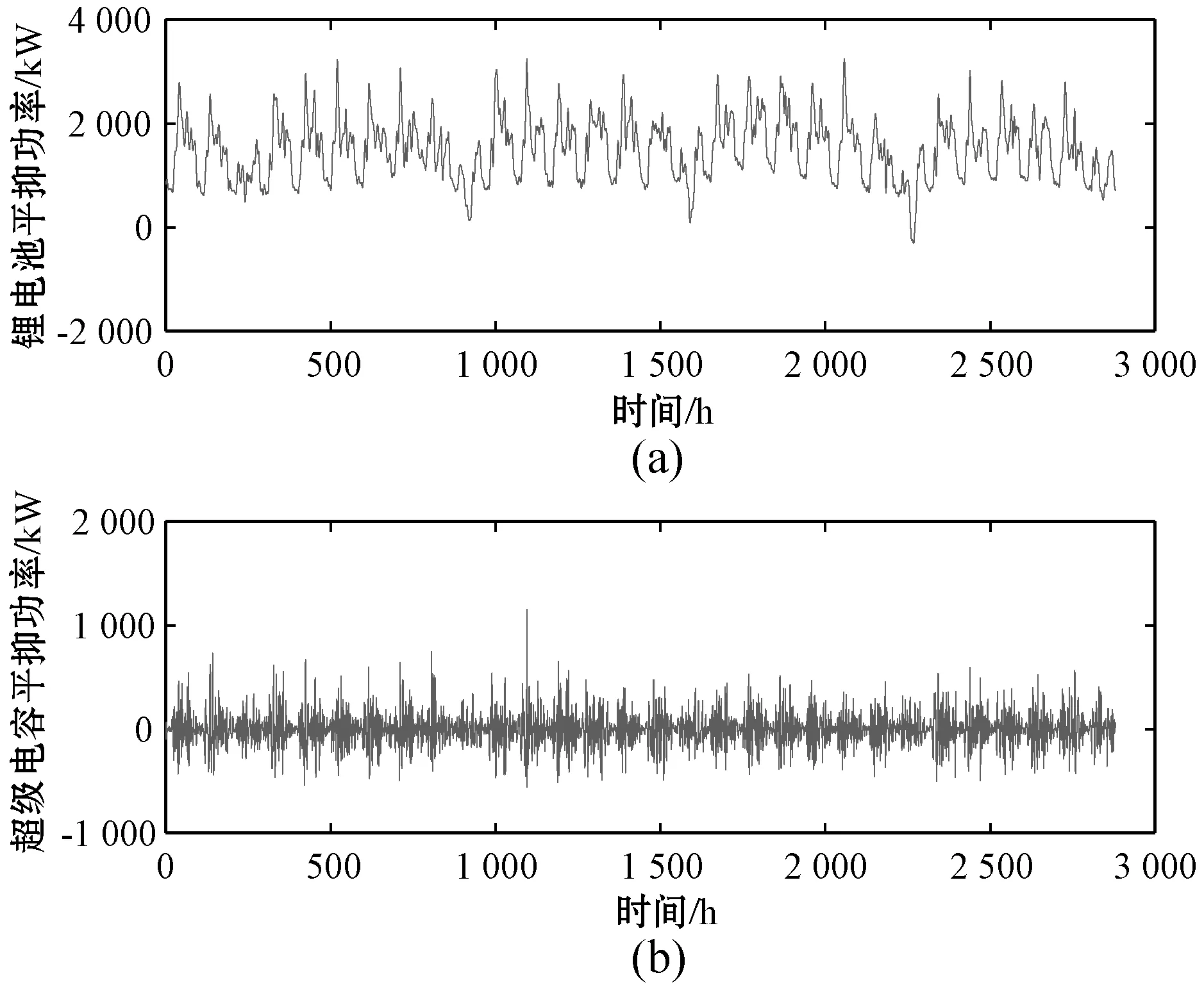
圖2 HESS系統平抑的高低頻分量

HESS的設計特征在功率密度、能量密度、壽命和成本方面各不相同；本文設定的HESS系統主要由Li-B和SC組成，兩者具有互補特性。高能量密度的Li-B能夠存儲大量電能，而SC具有高功率密度以便在充放電過程中提供快速響應。規劃HESS的主要目的是及時平抑瞬時功率并且最大程度節約單位時間內的壽命周期成本。HESS可以解決兩種儲能單獨使用時受能量密度和響應速度制約的問題，成為提高電網運行經濟性和穩定性的有效措施。所以，HESS里的Li-B和SC應對不同的平抑目標。具體地，Li-B被安排當作經濟調度的單元運行，而SC能夠彌補瞬時功率的不平衡。

本文所采用的HESS設備參數詳見表1，加裝的鋰電池相比于常規蓄電池擁有容量大、使用年限長、電能傳輸效率高、循環次數多等特點，未來將在儲能電站的建設中廣泛應用。但相比于超級電容器，鋰電池還不能進行高頻的充放電，且超級電容具有較高的可靠性，維護成本不高。如果單獨利用鋰電池對凈負荷進行平抑，配置容量性價比方面不高。另一方面，當鋰電池運行在較大放電倍率(C-rate)和放電深度(Depth of Discharge,DOD)等工況下，則一定程度上降低其壽命。因此，配置HESS可以形成資源互補，相比獨立的鋰電池配置能夠降低工業用戶的用電成本。

3 基于需量管理的混合儲能兩階段調度規劃模型

本文提出一種計及工業用戶用電需量的多時間尺度HESS容量配置和經濟運行兩階段模型。通過改進的CPSO優化受電側混合儲能配置運行方法來降低工業園區用戶總用電成本。當前，工業園區普遍執行兩部制電價計收，增強了模型的說服力。

3.1 兩部制電價機制

當前，中國大多數地區受電變壓器容量在315 kVA以上的工業用戶執行兩部制電價，容量在100～315 kVA的電力負荷可自行選擇兩部制或單一制。兩部制電價計收方式分為電度電價和基本電價，電度電價根據“峰—平—谷”階段分時電價計收，而基本電價則以月時間尺度根據受電變壓器容量(kVA)或最大需量(kW)計收。最大需量是從月用戶負荷曲線中提取出每個需量周期(本文取15 min)平均功率的最大值[17-18]。

需量管理是通過控制負荷需求，實現最大需求功率低于合同用電功率，并且通過管理降低合同用電功率，從而提高負荷利用率。本文通過優化需量系數降低用戶的最大用電需量，這個過程進一步減少了用戶基本電費的支出，在整體上提高用戶的需量收益。

3.2 一階段月度HESS容量優化配置優化模型

一階段月度HESS容量優化配置模型以規劃總成本F最小為優化目標，優化函數的變量包括鋰電池的額定功率及容量、超級電容器的額定功率及容量和最大需量。總成本F包括：電度電費、按需量計費的基本電費、HESS全壽命周期成本，以及波動率折算成本。

目標函數表示為：

minF1=C1+C2+C3+C4

(4)

式中：F1為月時間尺度優化配置總成本；C1為月電度電費成本；C2為用戶按月最大需量計費的基本電費成本；C3為折算到月周期的HESS全壽命周期成本；C4為波動率的折算成本。

月電度電費成本C1中功率測量的時間間隔為15 min，一天24 h共有96個功率點，具體公式為：

(5)

式中：T為每個月的天數，本文所設典型月為30天；m為分時電價；PL_bat(i,t)和PL_cap(i,t)為第i天t時刻鋰電池與超級電容的輸入功率；Pdis_bat(i,t)和Pdis_cap(i,t)為第i天t時刻鋰電池與超級電容的放電功率；Pch_bat(i,t)和Pch_cap(i,t)為第i天t時刻鋰電池與超級電容的充電功率；PL_HESS為輸入混合儲能系統總功率。

用戶按月最大需量計費的基本電費成本C2如下：

(6)

式中：a為可選擇基本電價；M表示最大需量；Ppeak表示實際需量值。

HESS全壽命周期成本C3考慮鋰電池和超級電容的綜合功率容量折算成本，具體公式如下：

(7)

式中：Spb、Seb、Spc和Sec分別代表鋰電池的功率單價和容量單價以及超級電容的功率單價和容量單價；Pmbat、Embat、Pmcap和Emcap分別代表鋰電池的額定功率和額定容量以及超級電容的額定功率和額定容量；Nbat、Ncap分別表示鋰電池的使用年限壽命和超級電容的使用年限壽命。

等效凈負荷波動性成本C4通過累加單位時刻間的凈負荷差值，并通過折算得出，公式如下：

(8)

式中：λ為波動折算因子。

在優化配置HESS容量時，應充分考慮以下約束條件：

(1) 電網能量守恒約束。光伏模塊出力、HESS功率與工業用戶負荷之和應與并網功率一致，合理進行電價交易。

(2) 混合儲能系統荷電狀態(SOC)約束。鋰電池和超級電容器的SOC都應當在合理的限定范圍內，過充過放會降低儲能的使用壽命；且不同種類儲能的SOC變化范圍也不同，應當根據所采用的儲能介質具體分析[19-20]。

(3) 混合儲能系統最大充放電功率約束。鋰電池與超級電容器的充放電功率的限制分別是其各自的額定功率。

(4) 負荷功率峰值約束。平抑后的負荷功率需要低于設定的峰值上限約束。

(5) 負荷功率波動率約束。平抑后的負荷功率前后時刻的差值需要滿足限值，滿足系統的波動性要求。

結合上述的分析，約束條件整理如下：

(9)

式中：Pex為電網與用戶交換功率；PPV、PHESS、PL分別表示光伏出力、混合儲能輸出功率、用戶負荷；SOCbat和SOCcap分別為鋰電池與超級電容的荷電狀態；Pbat和Pcap分別為鋰電池與超級電容的充放電功率；Ppeak_max為峰值約束的限值；Pflu_max為波動差額限值。

3.3 二階段日前調度優化模型

二階段日前調度模型以第一階段優化配置的功率和容量結果作為約束，優化的最大需量值作為該模型已知量。以24 h為周期、15 min為時隙對用戶的兩部制電費和波動性進行優化，進一步提高用戶的峰谷套利，具體表示為：

minF2=C1+C2+C4

(10)

式中：F2為日時間尺度優化運行調度成本。

該模型的約束條件與月度模型類似，滿足電網能量守恒約束、混合儲能系統荷電狀態(SOC)約束、混合儲能系統最大充放電功率約束、負荷功率峰值約束，以及負荷功率波動率約束。此外，模型將一階段優化出的鋰電池的額定功率和額定容量以及超級電容的額定功率和額定容量作為約束條件。公式如下：

(11)

式中：Pbat(t)和Pcap(t)分別為鋰電池與超級電容t時刻的充放電功率；Δt表示單位時間序列。

3.4 算法求解

本文采用改進的混沌粒子群算法(CPSO)[21-22]對雙階段模型進行優化求解。在粒子群算法中增加混沌映射，有利于增加粒子群算法的全局搜索能力。如果每次迭代都對粒子進行混沌化，可能會破壞粒子向最優解進化的趨勢。因此本文提出一種改進的CPSO，每次迭代時，根據粒子每維的值相對最優解此維度的值位置賦值為0、1、2、3，從而對每個粒子進行編碼。對粒子Pi的編碼規則如下：

(12)

式中：xmid1 j和xmid2 j為粒子上下限與xbest j之間的二分點，xmid1 j=(xbest j+xmin)/2，xmid2 j=(xbest j+xmax)/2；xij為粒子Pi第j維的數值；xbest j為當前迭代次數下的最優粒子第j維的數值，j=1,2,…,N。

可以得到每個粒子的編碼矩陣Mbin：

(13)

算法后期，粒子群傾向于集中在某極值附近，部分粒子的二進制編碼變得相同，為了防止陷入局部最優，可以通過設定編碼矩陣Mbin的閾值來判斷粒子的多樣性，并求解編碼矩陣Mbin的極大線性無關組，極大線性無關組對應的粒子具有多樣性，繼續回到PSO的迭代過程中，對剩余聚集度高的粒子混沌化，增強算法的全局搜索能力。

模型的上層容量配置層在月周期內以規劃總成本為目標，計算粒子的適應度值，優化出鋰電池與超級電容器的額定容量和額定功率四個變量以及最大需量M。確定HESS額定容量功率以及最大需量的基礎上，下層日前優化調度層進一步降低工業用戶的用電成本，以及減小對電網功率波動的影響。具體流程結構如圖3所示。

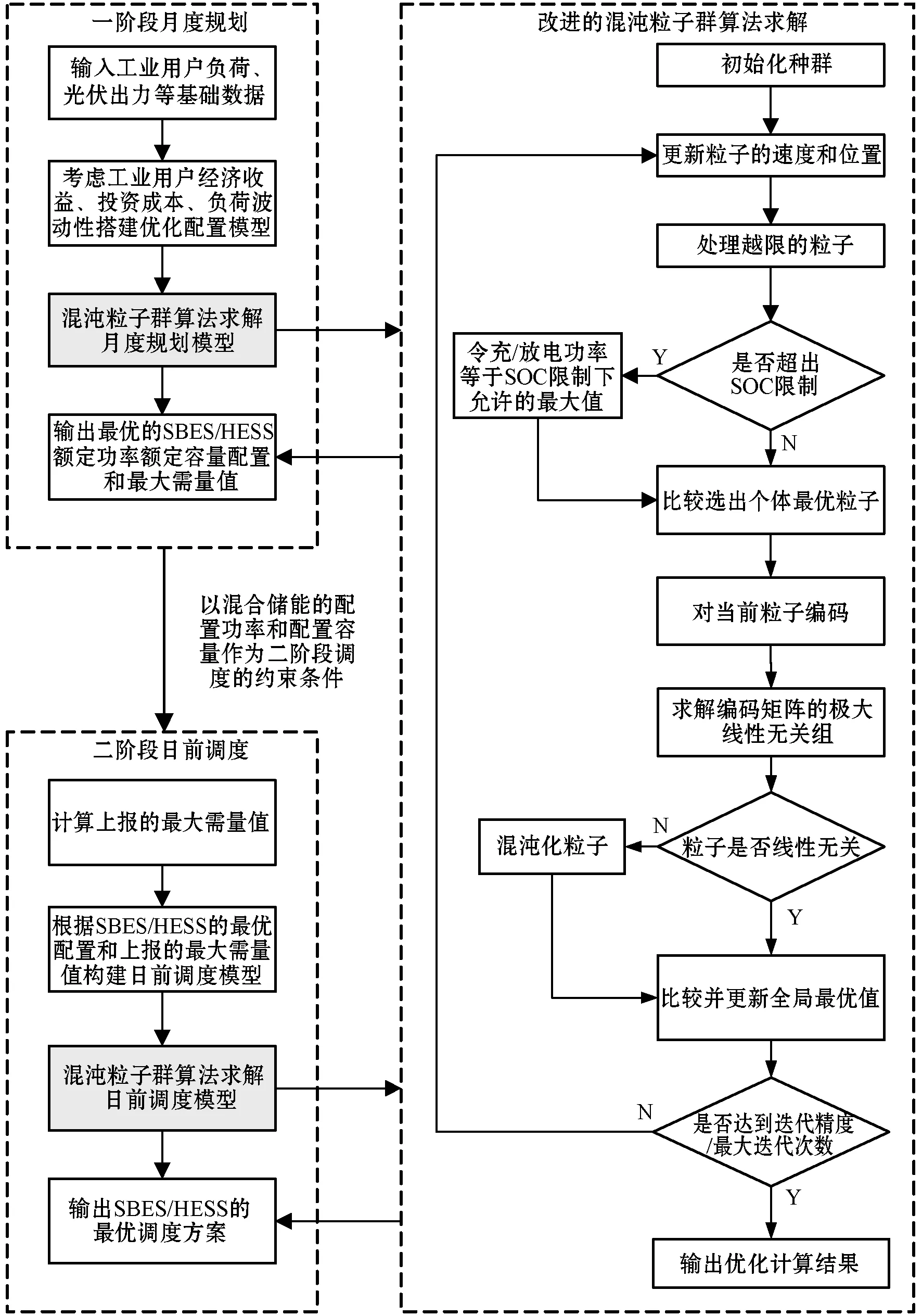
圖3 兩階段優化流程

4 算例分析

為了驗證HESS容量和功率配置以及經濟性的有效性，在MATLAB R2016a的開發環境下應用經驗模態分解技術將凈負荷功率分解成HESS平抑的高頻、低頻波動分量，并用改進的混沌粒子群算法對HESS模型與單儲能(SBES)模型分別進行兩階段優化對比。本文以江蘇某工業園區典型年負荷為仿真對象。工業凈負荷與分時電價如圖4所示。

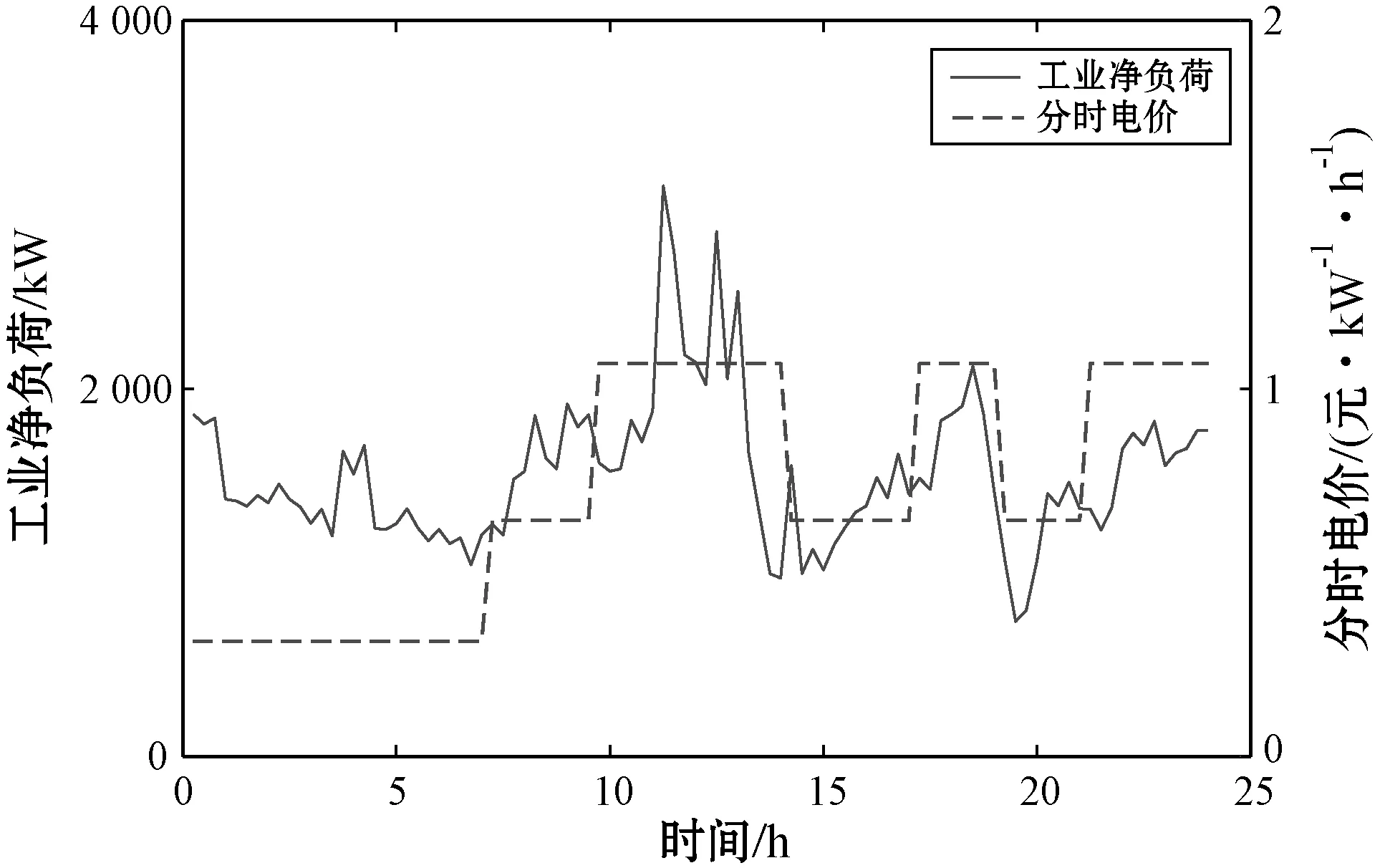
圖4 工業凈負荷與分時電價曲線

4.1 EMD分解結果

本文將大工業用戶負荷與光伏模塊發電數據合成出的等效凈負荷曲線分解成一系列IMF分量。如圖5所示，其中：c0代表原始凈負荷功率；c1-c5代表分解得到的各階IMF分量；r代表分解得到的趨勢性余項。可以看出:第1階IMF分量具有最高瞬時頻率成分，第5階IMF分量具有最低瞬時頻率成分，階數越高則所含瞬時頻率成分越低;第i階IMF分量的瞬時頻率幾乎是第i+1階IMF分量瞬時頻率的兩倍。根據頻率混疊情況選擇接近分頻頻率的c4選擇0.000 5 Hz作為分頻頻率能在混疊最少的情況下區分高低頻波動分量的k值。

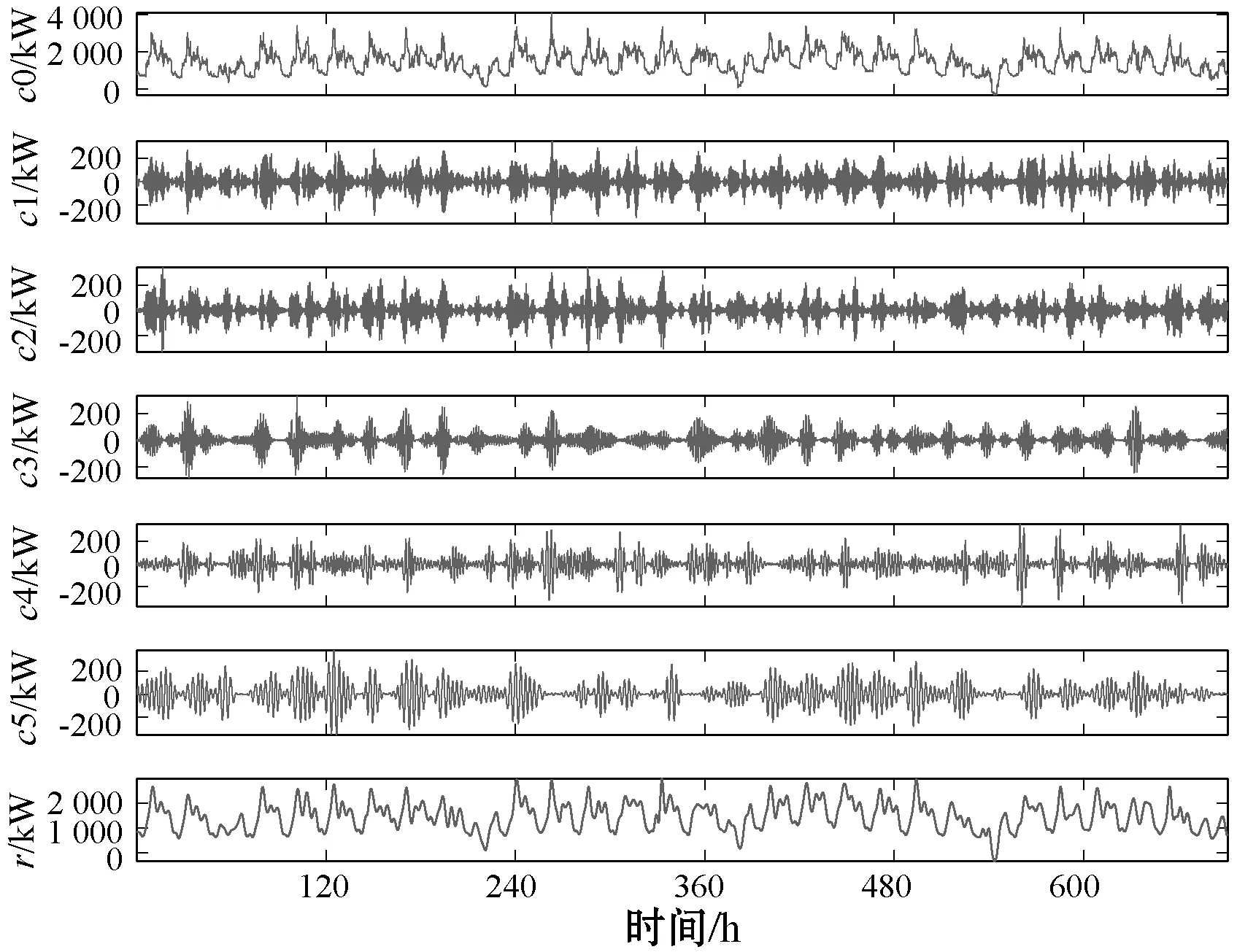
圖5 經驗模態分解凈負荷功率

4.2 優化參數設置與算法流程

本文以江蘇地區某工業園區11月份負荷作為典型月，月中選擇某日作為典型日研究，其合成凈負荷峰值為4 033.73 kW，光伏出力峰值為1 257.8 kW。混合儲能系統參數參照表1。所設電價參照江蘇省工業分時電價，高峰1.069 7元/kW·h，平段0.641 8元/kW·h，低谷0.313 9元/kW·h。可選擇基本電價，需量電價為40元/kW·mon，容量電價為30元/kVA·mon。

本文算法流程如圖6所示。

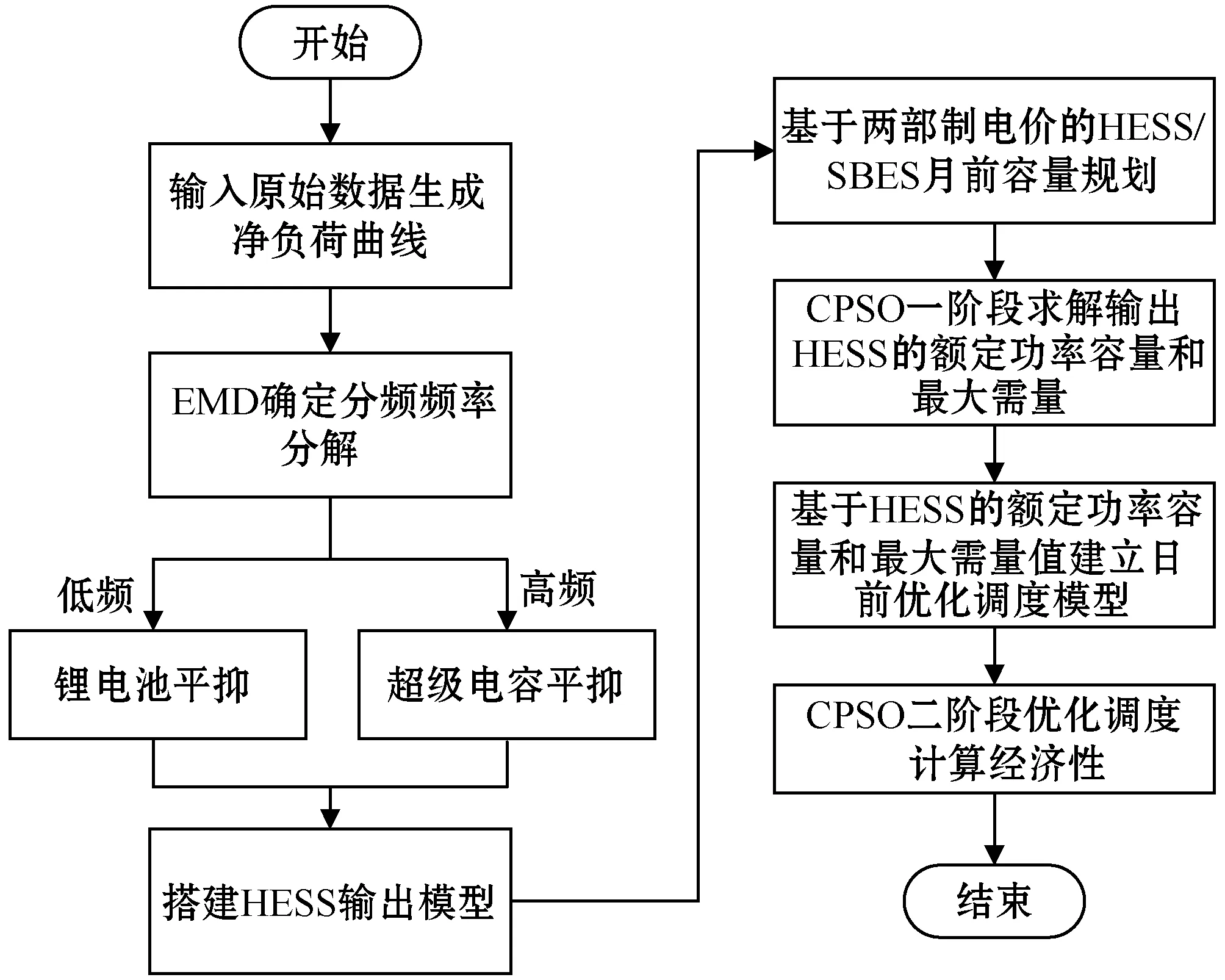
圖6 分頻優化流程

原始凈負荷曲線被EMD劃分所產生的高頻功率和低頻功率，分別被超級電容和鋰電池平抑。對HESS的容量進行優化配置，第一階段采用改進的CPSO求解額定功率、額定容量、最大需求量。第二階段建立日前調度模型，優化HESS最佳充放電功率，計算用戶的綜合成本。

4.3 儲能配置成本分析

采用HESS替換SBES，通過減少儲能配置成本來增加收益。利用改進的CPSO進行計算，所設最大迭代次數為200，迭代精度為10-3,與常規粒子群算法優化對比如圖7所示，改進的CPSO收斂速度變緩，適應度值更低，說明該方法更易搜尋到全局最優解。

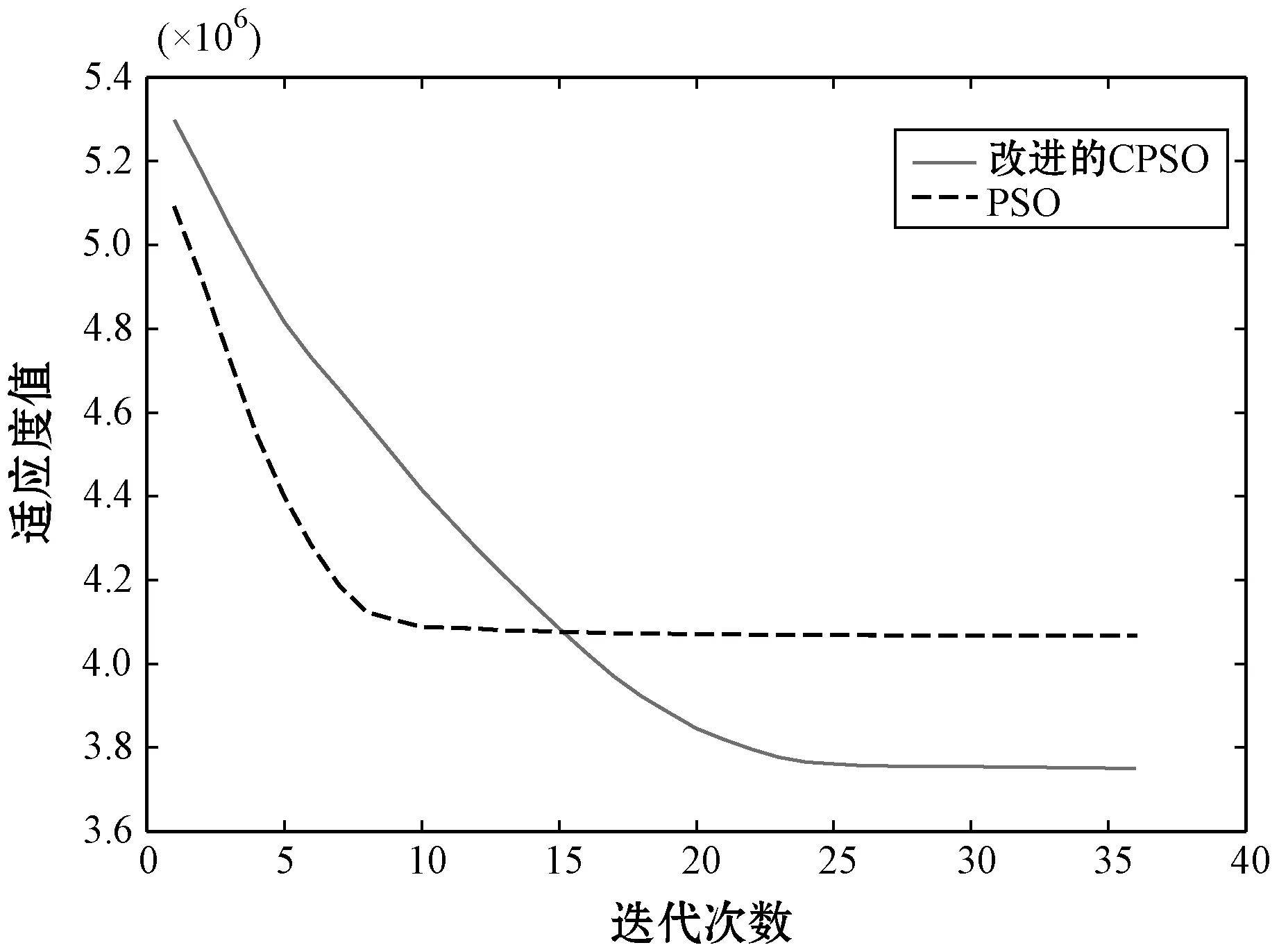
圖7 適應度值對比

優化結果如表2所示，HESS雖然多出SC的額定容量成本，但同時降低了Li-B的額定容量。雖然SBES和HESS的額定容量參數有區別，但可以實現相同的功率平抑效果。對照月均最小成本，采用SBES的月均最小成本為151 566.7元，而HESS的年均最小成本僅為136 427.2元，降幅約為10%。

表2 儲能優化配置結果對比

表3所示為無儲能配置、SBES與HESS配置經濟性對比，配置SBES相較于無儲能配置，即便多出一部分儲能成本，其總成本還是稍有下降。配置HESS的月均成本以及工業用戶總成本好于SBES的削峰填谷，其改進的混沌粒子群優化適應度要好于傳統粒子群優化結果；雖基本電費上升了8.34%，但電度電費、儲能月均成本分別下降19.39%、6.04%，工業用戶總成本少花費642 525元，下降17.8%。

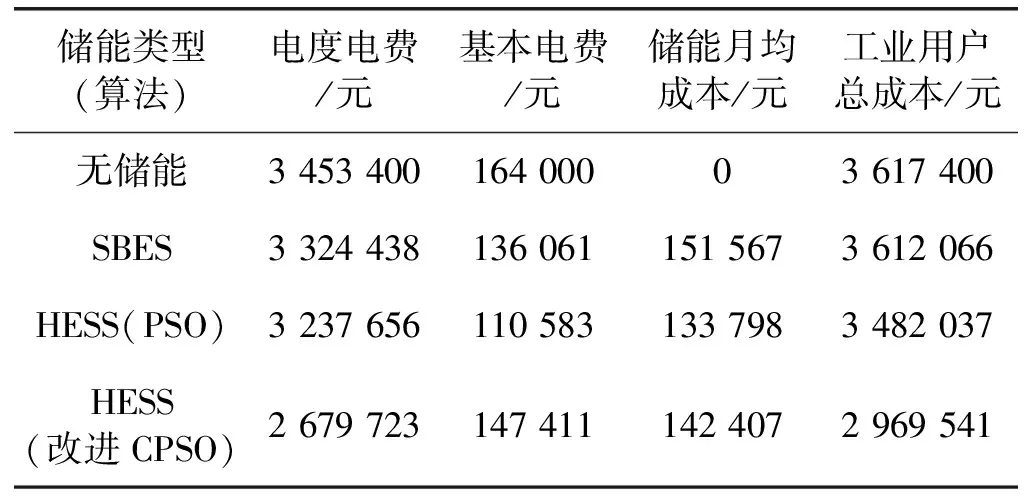
表3 儲能配置經濟性

4.4 典型日優化運行分析

二階段日前調度優化模型選用江蘇某輕工業園區典型日負荷數據，HESS和SBES優化的充放電功率分別如圖8-圖9所示，可以明顯看出，單儲能的充放電功率跟隨凈負荷的波動規律，而混合儲能工作時，可結合圖2對比，其鋰電池和超級電容器的充放電分別跟隨凈負荷低頻分量以及高頻分量的波動規律。

凈負荷的優化結果對比如圖10所示，HESS的削峰效果明顯好于單儲能平抑，其波動性也比單儲能小。具體地，單儲能的削峰率為34.78%，HESS的削峰率為43.92%。單儲能平抑的峰谷差是原始凈負荷曲線峰谷差的30.37%，HESS平抑的峰谷差是原始凈負荷曲線峰谷差的15.10%。圖11為HESS分頻優化結果，可以看出凈負荷高頻分量的劇烈波動基本上被超級電容所平抑，因此HESS的優化的凈負荷曲線比單儲能更加平滑，體現了HESS在提升用戶的用電質量、消除工業用戶并網的不利影響上的優勢。

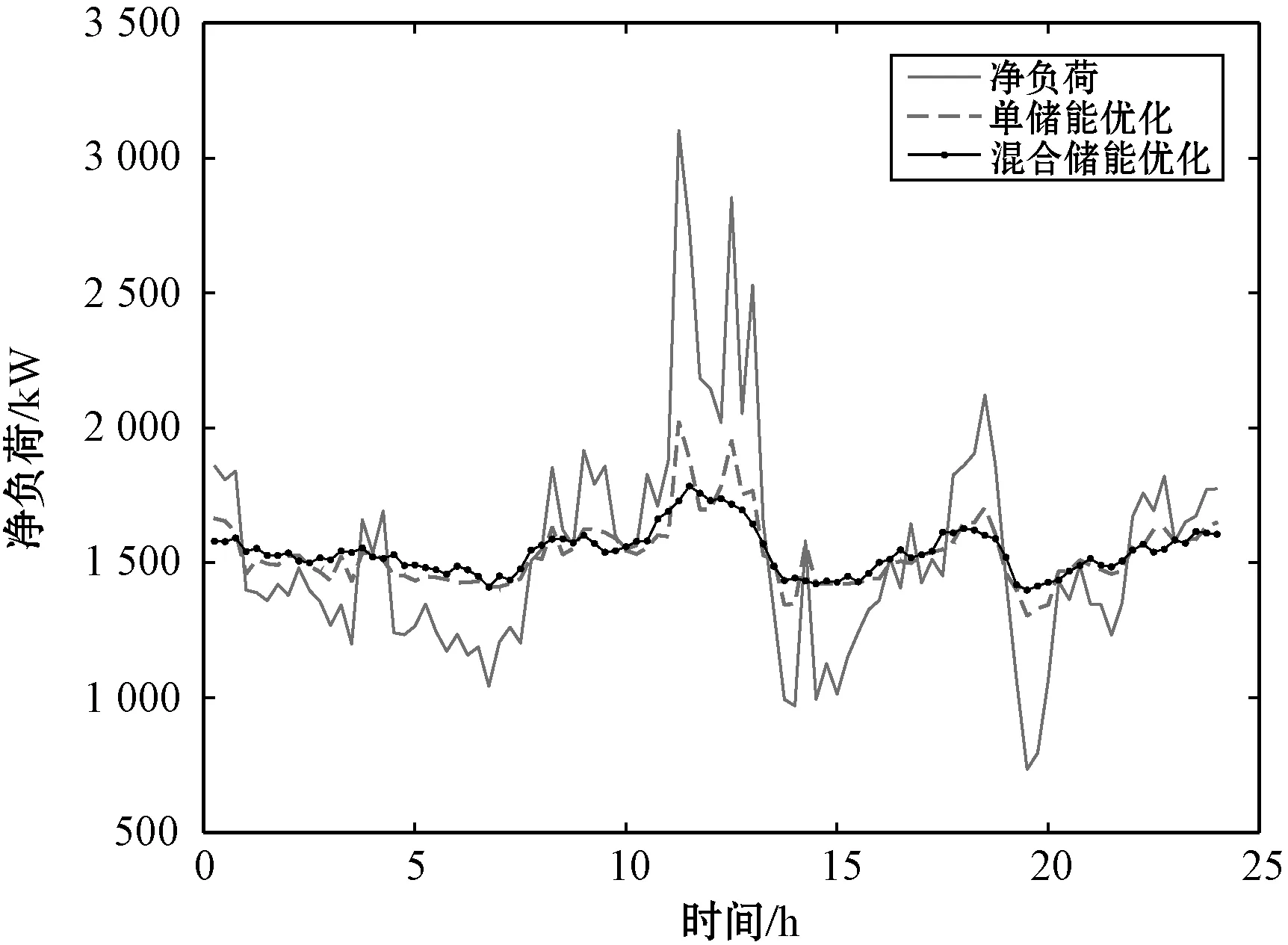
圖10 凈負荷優化對比

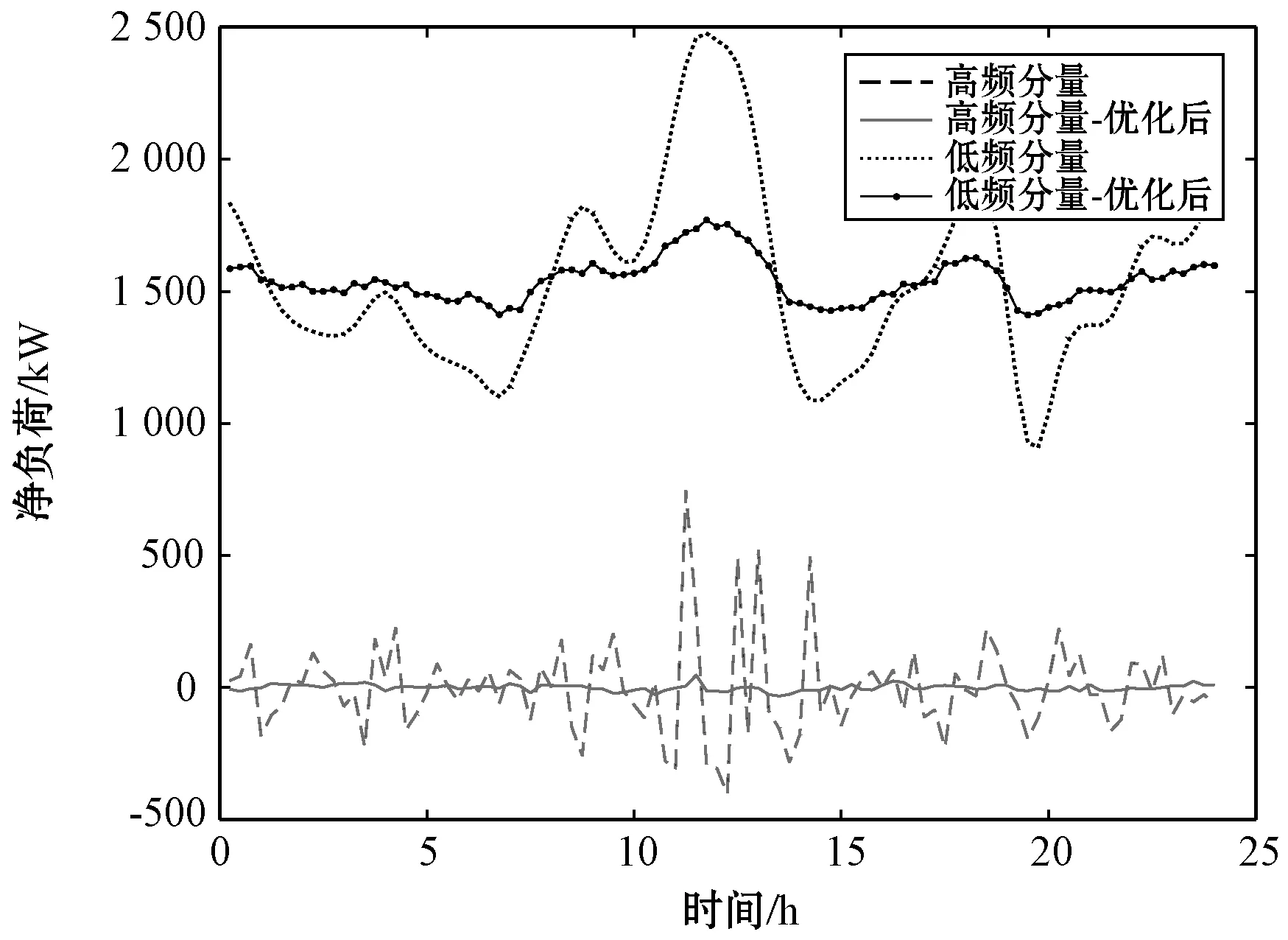
圖11 混合儲能分頻優化結果

5 結 語

本文采用EMD分解工業用戶凈負荷功率，由混合儲能平抑，對電池和超級電容器的容量配置進行了具體量化。建立了不同時間尺度的兩階段優化模型，在月度優化中，以用戶的總電費、HESS安裝成本、負荷的波動性最小作為目標函數，確定上報的最大需量以及HESS的容量配置。在日前優化中，以工業用戶收益最大和電能質量最優為目標函數，優化儲能充放電功率，進一步提高用戶的經濟收益。實例分析結果表明：

(1) 通過不同時間尺度的兩階段優化，應用改進的CPSO增加了全局尋優能力，提高了儲能系統的出力性能并降低儲能容量配置成本，進而提高了工業用戶儲能安裝收益。

(2) 相比單儲能優化，配置HESS可以降低用戶負荷的最大需量，相應地降低基本電費。同時，也減少了用戶側受電變壓器的配置容量，大幅降低工業用戶的用電成本，充分滿足工業用戶節約用電費用需求。

(3) 配置HESS有利于提升并網的工業用戶負荷的平滑度，實現電網與用戶的雙贏，有利于HESS商業化推廣。

本文后續的工作主要是針對HESS在工業用戶中的長期運行情況進行研究，進一步提高用戶收益，深入HESS在用戶側的應用研究。