基于隨機森林的光譜分類模型研究

摘要：文章第一節(jié)介紹集成算法原理;第二節(jié)系統(tǒng)理論地說明了Bagging算法;第三節(jié)介紹隨機森林算法;第四節(jié)介紹實驗內(nèi)容以及程序模塊，利用Python實現(xiàn)光譜數(shù)據(jù)的分類并評估結(jié)果，然后實行調(diào)參，得到最優(yōu)的參數(shù)搭配;第五節(jié)對優(yōu)化模型進行測試，與原模型比較準確率、查準率、召回率、F-score值等指標(biāo)，發(fā)現(xiàn)優(yōu)化后的結(jié)果優(yōu)良;第六節(jié)總結(jié)隨機森林算法的優(yōu)缺點。

關(guān)鍵詞：集成學(xué)習(xí);Bagging;隨機森林

中圖分類號：TP273.4 文獻標(biāo)識碼：A? 文章編號：2096-4706（2021）07-0081-04

Study on Spectral Classification Model Based on Random Forest

YUAN Zhengxi

（South China Normal University，Guangzhou? 510631，China）

Abstract：In this paper，the first section introduces the principle of the ensemble algorithm;in the second section，the Bagging algorithm is explained systematically and theoretically;the third section introduces the random forest algorithm;the fourth section introduces the experimental content and program modules，Python is used to classify the spectral data and evaluate the results，and then adjust the parameters to obtain the optimal parameter matching;the fifth section tests the optimized model and compares the indexes of the accuracy，precision，recall and F-score value with the original model. It is found that the optimized result is excellent;the sixth section summarizes the advantages and disadvantages of random forest algorithm.

Keywords：ensemble learning;Bagging;random forest

收稿日期：2021-03-20

0? 引? 言

機器學(xué)習(xí)，一般來說是致力于研究如何通過計算的手段、利用經(jīng)驗來改善系統(tǒng)自身性能的一種方法。對于機器學(xué)習(xí)而言，“經(jīng)驗”往往是以數(shù)據(jù)形式儲存起來的。機器改善性能的方法是通過數(shù)據(jù)的不斷訓(xùn)練產(chǎn)生“模型”，繼而使得該“模型”能夠盡可能地適用于更多的數(shù)據(jù)。目前，機器學(xué)習(xí)有多種算法，比如：決策樹、神經(jīng)網(wǎng)絡(luò)、支持向量機、貝葉斯分類、LDA，等等。通常來說，一個研究可以使用多種算法，而集成學(xué)習(xí)則能夠結(jié)合多個算法使得機器學(xué)習(xí)具有更好的效果以及更優(yōu)越的泛化性能。

1? Bagging算法

集成學(xué)習(xí)的方法有并行和串行兩種，Bagging算法是并行式集成學(xué)習(xí)方法最著名的代表。Bagging是基于Boostrap Sampling采樣方法，給定m個樣本的數(shù)據(jù)集，隨機取出一個樣本，接著再把剛才抽到的樣本放回數(shù)據(jù)集中，由此使得下一次抽樣的數(shù)據(jù)集與上一次的情形完全相同。這樣，經(jīng)過m次抽取，我們得到m個樣本集。根據(jù)Boostrap Sampling采樣方法，這m個樣本集里的某些元素可能重復(fù)多次，也可能有部分樣本未出現(xiàn)在樣本集中。

相比于其他集成學(xué)習(xí)方法，Bagging算法更為高效，其學(xué)習(xí)復(fù)雜度和學(xué)習(xí)器是同階的。另外，Bagging可以直接用于多分類和回歸等任務(wù)。再者，Bagging可以降低方差，因此把它使用到不剪枝的決策樹上效果非常好。這也為隨機森林算法的出現(xiàn)奠定了基礎(chǔ)。

2? 隨機森林

隨機森林是使用多棵決策樹對樣本進行訓(xùn)練并預(yù)測的一種集成分類器，該分類器最早由Leo Breiman和Adele Cutler于1995年提出。它以決策樹為基學(xué)習(xí)器，使用Bagging集成方法，并在此基礎(chǔ)上引入隨機屬性的選擇。隨機森林有許多優(yōu)勢：算法簡單、易于實現(xiàn)、計算開銷小等，其甚至被譽為“代表集成學(xué)習(xí)技術(shù)水平的方法”。

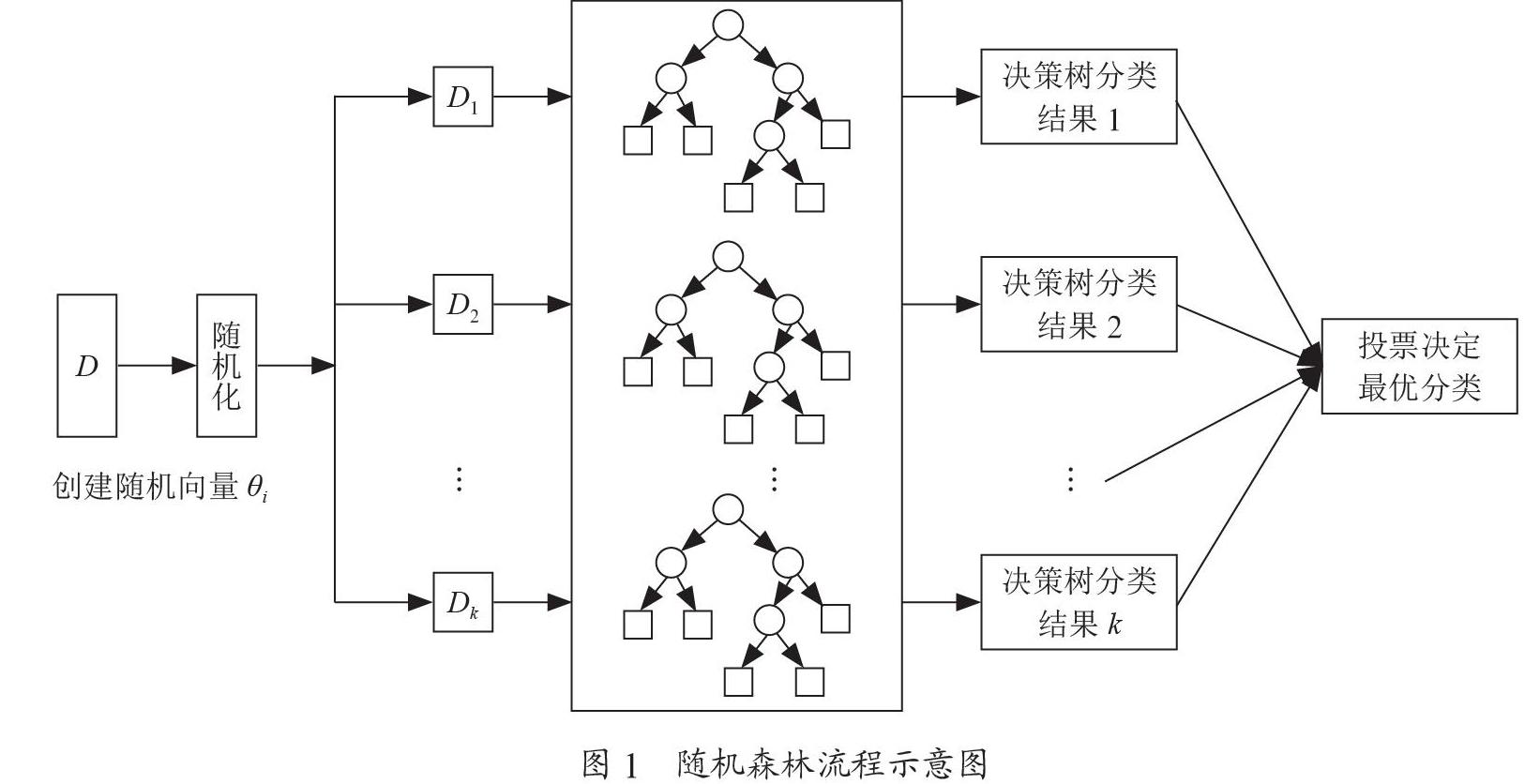
簡單來說，隨機森林分為四個步驟：第一，使用Bagging方法形成每棵樹的訓(xùn)練樣本集;第二，隨機選取分裂屬性集，假設(shè)當(dāng)前節(jié)點共有d個可用屬性，指定一個屬性數(shù)k（k≤d），從d個屬性中隨機抽取k個屬性作為分裂屬性集，并從分裂屬性集中選擇最優(yōu)屬性用于數(shù)據(jù)劃分;第三，每棵樹任其生長，不進行剪枝;第四，根據(jù)投票法則對樣本類別進行投票。

具體形式如圖1所示，設(shè)數(shù)據(jù)集為D且創(chuàng)建k棵決策樹，則對應(yīng)有k個隨機向量θi（其中i=1，2，…，k），數(shù)據(jù)集D在每個θi對應(yīng)有一個子集數(shù)據(jù)集供Di第i棵決策樹學(xué)習(xí)，得到?jīng)Q策樹分類結(jié)果i。最后利用投票決定最優(yōu)的分類結(jié)果。

3? 實驗及調(diào)參優(yōu)化

3.1? 數(shù)據(jù)預(yù)處理

3.1.1? 標(biāo)準化處理

采用z-score標(biāo)準化。這種方法基于原始數(shù)據(jù)的均值和標(biāo)準差進行數(shù)據(jù)的標(biāo)準化。定義均值為u，方差為σ，x為原始數(shù)據(jù)，則標(biāo)準化后新數(shù)據(jù)x'計算方式如式（1）所示：

（1）

3.1.2? 連續(xù)值處理

一般地，我們考慮將連續(xù)值離散化以適應(yīng)決策樹模型。這里，我們應(yīng)用二分法對連續(xù)值進行處理。

給定樣本集D和連續(xù)屬性a，假定a在D上有n個不同的取值，將這些值從小到大進行排序，得到序列（a1，a2，…，an）。對于該序列，選擇一個a屬性取值m，則可以把D分成兩個子集A、B。第一個子集A包含那些在屬性a上取值不大于m的樣本，另一子集B則包含那些在屬性a上取值大于m的樣本。如此，只要取值m在[ai，ai+1）上，m的劃分結(jié)果就不變。這樣，n個屬性值就形成n-1個離散值。由此，我們定義一個長度為n-1的序列M，第i個元素取值如式（2）所示：

（2）

即把區(qū)間[ai，ai+1）的中位點作為劃分點。然后，我們就可以像離散屬性值一樣來考察這些劃分點，選取最優(yōu)的劃分點進行樣本集合的劃分。

3.2? 實驗流程

我們采用隨機森林算法，使用Matlab實現(xiàn)對數(shù)據(jù)的分類，將代碼劃分為訓(xùn)練、測試、調(diào)度三個模塊。

在訓(xùn)練模塊中，如表1所示，首先輸入訓(xùn)練集;第一步，初始化隨機森林;第二步，循環(huán)生成N次隨機森林，其中每次循環(huán)都對單棵樹進行初始化，然后使用有放回采樣的方法從訓(xùn)練集中抽樣，使用的函數(shù)有“sort”和“randsample”;第三步，利用二分法將所選擇的連續(xù)屬性離散化;最后，輸出含N棵決策樹的隨機森林。

訓(xùn)練模型為整個實驗的核心，因此將訓(xùn)練模塊的關(guān)鍵代碼特別進行展示，以下為代碼清單：

#-*-coding： utf-8 -*-

%train為存放train_x（trian{1}）， train_y（train{2}）的cell 1*2

%? ?其中train_y 為k*1矩陣;矩陣存放標(biāo)簽

%? ?數(shù)據(jù)都已標(biāo)準化

%? ?test與train數(shù)據(jù)結(jié)構(gòu)類似

%? ?N：為隨機森林內(nèi)決策樹的數(shù)量

%? ?m：為抽取樣本量占總樣本量的比例

%? ?theTrees：為含有N棵決策樹的隨機森林（cell*N）

%% 初始化隨機森林

theTrees=[];

global Tree;

%%循環(huán)N次生成隨機森林

for i=1：N

%%單棵樹的初始化

TrainIndex=[];

train_x=[];

train_y=[];

Tree=[];

attr_list = cell（size（train{1}，2）， 1）;

attr_value_list=[];

Tree=struct（'father_Node_name'，[]，'Node_name'，[]， 'best_Attr'，[]， ... 'best_breakpoint'，[]，'MostVal'，[]）;

%%有放回采樣訓(xùn)練集

TrainIndex =sort（randsample（size（train{1}，1），round（size（train{1}，1）*m），true））;

train_x=train{1}（TrainIndex，：）;

train_y=train{2}（TrainIndex，：）;

%% 以下步驟為把所選的屬性離散化

for i1 = 1 ： size（train{1}，2）

attr_value_list = unique（train_x（：，i1））;

%利用二分法將連續(xù)屬性離散化

attr_list{i1} = （attr_value_list（2 ： end） + attr_value_list（1 ： end - 1）） / 2;

end

%% 開始生成樹

TreeGenerate（'root'， train_x， train_y， attr_list）;

Tree（1）=[];

theTrees{i}=Tree;

end

end

在測試模塊中，如表2所示，首先輸入測試集;第一步，初始化數(shù)據(jù)，添加若干空列表用于接下來儲存數(shù)據(jù);第二步，利用訓(xùn)練模塊得到的隨機森林模型對測試機數(shù)據(jù)進行預(yù)測;第三步，根據(jù)投票原則生最終預(yù)測結(jié)果，投票采用的方法是“相對多數(shù)投票法”。使用Matlab里的“tabulate”函數(shù)，計算出某樣本不同類別對應(yīng)的分類概率，從而選擇概率最高的一類作為最終的所屬類別;最后，輸出測試集的分類結(jié)果。

在調(diào)度模塊中，如表3所示，首先讀取訓(xùn)練數(shù)據(jù)、測試數(shù)據(jù)、標(biāo)簽集和光譜型的7種類型;第一步，調(diào)用訓(xùn)練模塊;第二步，調(diào)用測試模塊;第三步，評估結(jié)果即測試隨機森林的精度;最后，計算程序運行時間并輸出分類準確率。

3.3? 實驗數(shù)據(jù)

本文運用的數(shù)據(jù)是LAMOST平臺提供的恒星光譜數(shù)據(jù)，該樣本數(shù)據(jù)有481個屬性，其中訓(xùn)練集保存了159條樣本數(shù)據(jù)和標(biāo)簽，測試集保存了200條樣本數(shù)據(jù)和標(biāo)簽。每條數(shù)據(jù)的標(biāo)簽有三列信息，第一列是對應(yīng)光譜數(shù)據(jù)的光譜型，第二列是光譜次型，第三列是光度型。本文只對第一列的光譜型數(shù)據(jù)進行分類，其他兩列類同。

3.4? 實驗結(jié)果

運行程序，我們得到隨機森林算法對數(shù)據(jù)庫的分類效果。默認使用50個子樹數(shù)量、8個特征數(shù)量，得到準確率約為82%。

4? 模型優(yōu)化及測試

4.1? 模型優(yōu)化

為了得到更滿意的學(xué)習(xí)效果，本文需要盡量遍歷盡可能多的組合方式，找到最優(yōu)分類效果。假設(shè)樣本特征數(shù)為N，我們分別使用“50、100、1 000、1 500”子樹數(shù)量與N個、8個、log2N個、 √N個特性數(shù)量兩兩搭配，運行結(jié)果如表4所示。

由表4可知，當(dāng)取子樹棵樹為1 500、特征數(shù)量為√N時，能達到最高86%的準確率。因此對于本次分類任務(wù)，本文認為使用上述搭配效果最佳。

4.2? 模型測試

雖然得到了更好的參數(shù)搭配，但是我們還要測試優(yōu)化模型在該參數(shù)搭配下的其他性能。為此我們重復(fù)100次實驗，統(tǒng)計每次實驗下原模型和優(yōu)化模型的準確率，計算100次實驗中兩個模型的平均準確率。

由于隨機森林采取的是有放回的隨機抽樣，因此每次運行的準確率略有不同，故通過這種方法得到的準確率波動是具有參考價值的。通過這樣的比較，我們希望看到的是優(yōu)化后的模型比原模型具有更好的穩(wěn)定性以及更高的預(yù)測準確率，甚至可以有更高的查準率、召回率以及F-score值。于是，我們分別運行原模型和優(yōu)化模型，得到各自的預(yù)測準確率，繪制它們的對比圖，詳情如圖2所示。

原模型取子樹棵樹為50，特征數(shù)量為8時的預(yù)測準確率波動圖;優(yōu)化模型選取子樹棵樹為1 500，特征數(shù)量為√N的預(yù)測準確率波動圖。兩模型均值和方差對比如表5所示。

對比發(fā)現(xiàn)，原模型平均準確率是82.48%，優(yōu)化后的預(yù)測準確率在85.22%上下波動，比原來提高2.00%以上。另外，原模型準確率最低是77.80%，最高是86.70%，最大波幅4.00%以上;優(yōu)化模型準確率最低為83.10%，最高為87.30%，波幅不超過2.20%，最大波幅比原來減小2.00%以上。

由表5可以看出，調(diào)參之后隨著生成子樹的數(shù)量的提高，模型的穩(wěn)定性也提高了，同時隨著選取特征數(shù)量的調(diào)整，預(yù)測準確率也有所上升，達到了預(yù)期目標(biāo)。

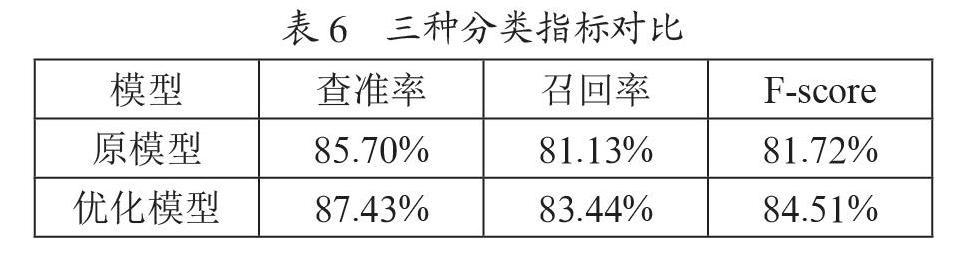
接著，再來看看原模型和優(yōu)化模型在micro算法下運行100次的查準率、召回率以及F-score值這三種分類指標(biāo)的均值，如表6所示。

顯然，優(yōu)化模型三種分類指標(biāo)均有明顯提升。綜上所述，優(yōu)化后的模型具有比原模型更好的穩(wěn)定性以及更高的預(yù)測準確率，甚至可以有更高的查準率、召回率以及F-score值。故此可以采納該參數(shù)配置的隨機森林算法。

5? 結(jié)? 論

本文介紹了機器學(xué)習(xí)，講解了集成學(xué)習(xí)的Bagging算法，重點放在Bagging中的隨機森林上，并用Matlab代碼實現(xiàn)了隨機森林算法。

對于隨機森林，其優(yōu)點是具有極高的準確率;它引入隨機性，使得隨機森林不容易過擬合，具有很好的抗噪聲能力，對異常點/離群點不敏感;而且它能夠處理很高維度的數(shù)據(jù)，并且不用做特征選擇;隨機森林還可以得到變量重要性排序。其缺點是相比于其他算法，隨機森林的輸出預(yù)測可能較慢。

用Matlab實現(xiàn)隨機森林算法的難點在于算法的子函數(shù)很多，邏輯關(guān)系較為復(fù)雜，代碼需要調(diào)試很久。

應(yīng)用隨機森林算法的難點在于參數(shù)調(diào)整是否合適，另外，訓(xùn)練樣本集、隨機劃分和選擇屬性也很重要。

參考文獻：

[1] 周志華.機器學(xué)習(xí) [M].北京：清華大學(xué)出版社，2016.

[2] 方匡南，吳見彬，朱建平，等.隨機森林方法研究綜述 [J].統(tǒng)計與信息論壇，2011，26（3）：32-38.

[3] 董樂紅，耿國華，高原.Boosting算法綜述 [J].計算機應(yīng)用與軟件，2006，23（8）：27-29.

[4] 胡永德.海量光譜數(shù)據(jù)降維方法的研究與應(yīng)用 [D].濟南：山東大學(xué)，2021.

[5] BREIMAN L. Random forests [J].Machine Learning，2001，45（1）：5-32.

[6] 周惠慧.恒星天文光譜數(shù)據(jù)分類方法探究 [J].信息與電腦（理論版），2021，33（7）：84-86.

[7] 劉曼云，趙正旭，王威，等.LAMOST恒星光譜數(shù)據(jù)分析 [J].信息技術(shù)與信息化，2019（11）：193-197.

作者簡介：袁正熙（2000—），男，漢族，廣東東莞人，本科在讀，研究方向：應(yīng)用統(tǒng)計。