一種基于“移去-恢復”理論的重力數據格網化方法

馮進凱，王慶賓，趙東明，楊 洋，黃子炎，黃 炎

（1. 信息工程大學，鄭州 450001；2. 鄭州大學，鄭州 450001）

重力數據是研究重力場理論和應用的基礎。為使用的方便，重力數據一般需要以等經緯度格網的數字形式存儲，以格網中點重力值表征網格區域內重力場特征。但在實際測量過程中，實測點通常按照測線方式推進、閉合。而且測量過程中容易受到地形等外界因素的干擾，實際測量數據不一定是格網中點的重力值，這就需要對實測重力點進行格網化，使其按照一定的分辨率等經緯度排列，以利于重力數據的建模和應用[1]。

傳統的重力數據格網化的本質是數學擬合，其原理是對已知的離散重力實測數據進行數學內插或外推，從而求得未知點（格網點中點）的重力值。常用的方法有曲面擬合法、反距離加權法[2]、Shepard 擬合方法[3]、Kriging 方法[4,5]以及最近興起的BP-神經網絡和深度學習擬合算法[6]，這些方法從二維數值擬合的角度出發處理重力實測數據，達到了一定的精度，但是這類方法忽略了重力場數據本身具有的物理特性。文獻[7]研究表明，由于地球重力場信號的中高頻部分和地形之間存在較強的函數關系，在一定范圍內，地形數據和重力數據展現出極強的相似性。而且，現階段全球地形數據已經能達到相當的精度和分辨率，這為利用結合地形數據進行重力數據的格網化奠定了基礎。基于此，本文利用重力場數據頻譜疊加原理，在顧及重力數據物理特性的基礎上結合實驗區地形數據，提出一種基于“移去-恢復”理論的重力數據格網化方法，設計出“計算-移去-推估-恢復”的四步重力數據格網化方法（簡稱“移去-恢復”法），實驗結果表明，相比于傳統的Kriging 格網化方法，本文提出的方法在精度上有一定的提升，算法穩定性更高，自洽性更好，而且格網化結果能夠反映目標區域更多的局部特征。

1 原理和方法

1.1 均衡理論

根據均衡理論[8]，均衡異常應滿足浮平衡理論，即均衡重力異常ΔgI理論上應滿足如下條件：

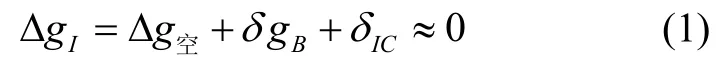
其中， Δ g空為空間重力異常，δ gB和 δIC分別為布格改正和地形均衡改正。布格改正δ gB可表示為：

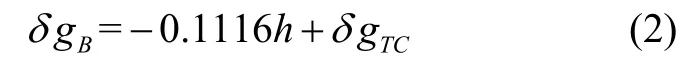
其中，h 為高程， - 0 .1116h 為層間改正，δgTC為局部地形改正。在局部平面坐標系下，局部地形改正計算時，為了兼顧計算精度和效率，通常將積分區域σ 劃分為中央區 σ0和遠區σ -σ0，中央區采用棱柱積分法，遠區采用線性卷積方式逼近真實積分[9]：

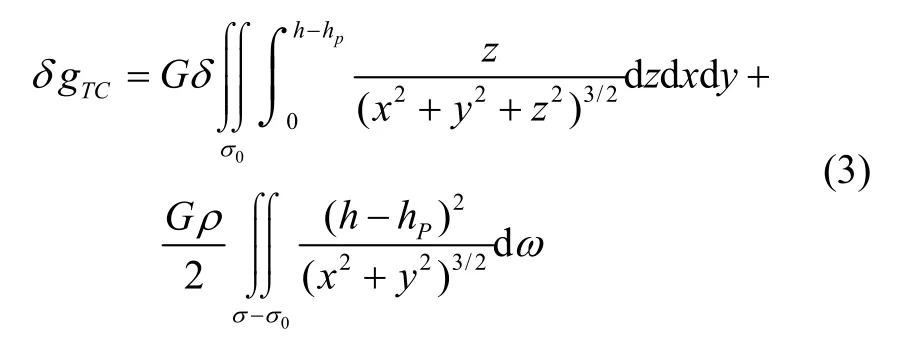
其中，( x , y , z )為流動點平面坐標，G 為萬有引力常量，δ 為地球密度常數，h 和 hp分別為流動點和計算點高程。

均衡改正采用較為符合地球實際均衡狀態的Airy—Heiskanen 模型[10,11]，該理論認為常密度的地殼漂浮在密度為 ρm的地幔上并保持平衡，超出海平面的部分或低于海平面的部分分別在均衡面以下的部分以“山根”或“反山根”的形式進行補償。在局部平面直角坐標系下，直接給出均衡改正的計算表達式：

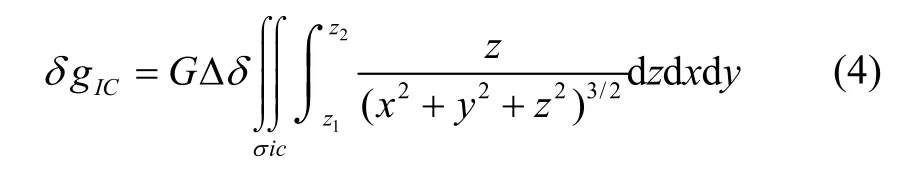
其中，z2=- T，z1=-（ T+t） ，T 為均衡面深度，t 為補償深度， Δδ 為地殼和地幔部分的密度差，均衡改正計算方法參照局部地形改正。一般來說，空間重力異常變化較為劇烈，在構造高分辨的格網數據時對測點的密度要求較高，而均衡重力異常變化較為平緩，對測點的密度要求較低，比較適合重力點的格網化。

1.2 Kriging 法

Kriging 方法是一種常用的擬合方法，廣泛的應用于數據處理以及工程應用等領域，從本質上講，該方法是利用區域原始數據對估計點進行的最優無偏估計[4,5]。其滿足以下條件：

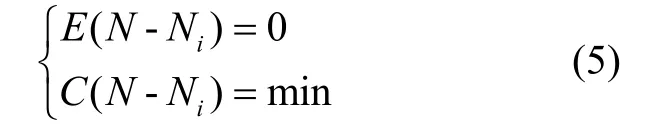
其中，E 與C 代表數學期望與方差，N 與 Ni分別表示計算點與擬合點的大地水準面高。插值模型如下：

其中， λi為每個擬合點的權值。通常利用變異函數代替方差元素：

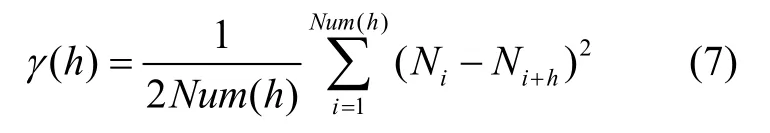
其中，h 表示滯后距，Num(h) 表示滯后距個數，詳細推導見文獻[5]。

1.3 “移去-恢復”方法

“移去-恢復”理論在局部重力場建模中有著廣泛應用[12,13]，基本思想為：根據重力場頻譜疊加性原理將重力場信號分為低頻、中頻、高頻三部分，重力場元看作不同頻段重力場信號的組合。隨著重力衛星技術的發展，低頻信號已能達到相當精度，高頻和超高頻部分主要來自地形起伏影響，可以通過高分辨率的地形數據計算得到。在計算時，移去輸入數據的低頻、高頻信號，對殘余值進行建模計算，最后在計算結果中恢復相應頻段的重力場信號，即可得到計算點完整頻段的重力場元數據[4,14]，其計算步驟可簡單概括如下：

（1）首先在重力場元中移除低頻和高頻頻段信息，獲得殘差重力場元；

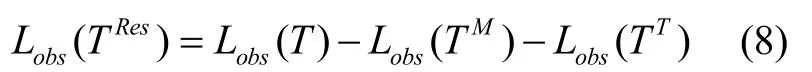
其中，L表示擾動位T 的泛函，TRes為殘余擾動位，TM和TT分別為低頻信號和高頻信號。

（2）利用步驟（1）中產生的殘差重力場信息結合適當的建模方法進行模型構建；

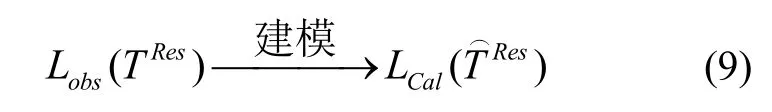
（3）最后，在計算點中恢復步驟（1）中移去的低頻和超高頻信息。

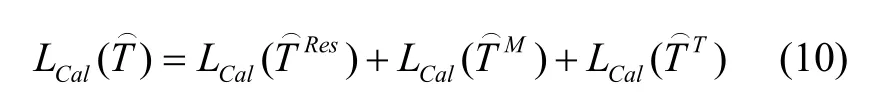
需要注意的是，“移去-恢復”過程中，移去和恢復的部分必須是可以在一定的精度條件下精確計算得到的，否則“移去-恢復”過程將無法完成。

同理，公式(1)可改寫為如下形式：

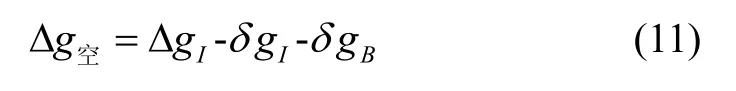
空間重力異常可以看作是布格改正、均衡改正和均衡異常三種信號的疊加，從1.1 中可以看出，布格改正和均衡改正均與地形數據相關，可通過地形數據和地殼、地幔密度信息計算得到，符合“移去-恢復”理論的基本前提。現將“移去-恢復”理論應用到重力數據格網化中，基本思路可概括為“計算-移去-推估-恢復”四步，具體計算步驟如下：

（1）計算：根據Airy 均衡理論，利用式(2)-(4)并結合高精度、高分辨率的地形數據和密度信息計算目標區域內布格改正和均衡改正的改正項；

（2）移去：利用式(1)在建模點的空間重力異常中移去地形數據產生的影響（布格改正、均衡改正），得到在建模點較為平滑的均衡重力異常；

（3）推估：利用1.2 中介紹的Kriging 格網化方法對均衡重力異常進行格網化，獲取目標點的均衡重力異常數據；

（4）恢復：利用步驟（1）計算的數據，在目標點均衡重力異常的基礎上恢復地形數據的影響，即可得到目標點的空間重力異常，公式如下：

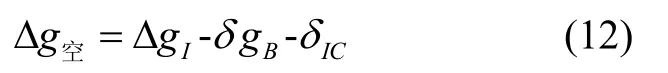
2 數值實驗

實驗區位于南非共和國境內的馬塔貝萊高原，范圍如圖1 所示，實驗區內地形變化劇烈，重力場信號復雜，地形數據采用美國國家地球物理數據中心(NGDC)開發的Etopo1 的1′分辨率格網化地形數據[15]，實驗區內最大高程落差 2334 m，平均高程1052.2284 m，選用離散點所在地形格網為離散點高程，顧及地形改正和均衡改正邊界效應，選取圖1 紅框部分為中心計算區域。從“GRAVCD-africa”數據集中搜集到計算區1789 個實測空間重力異常數據（圖1 中三角點和圓點），地形數據和實測點空間重力異常數據統計信息見表1。

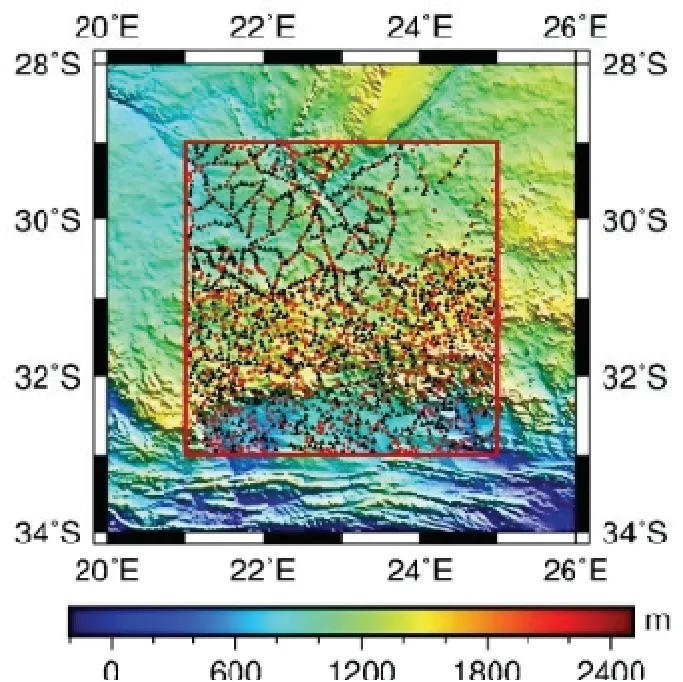
圖1 實驗區域高程及點位分布示意圖Fig.1 Elevation and points distribution of the experimental area

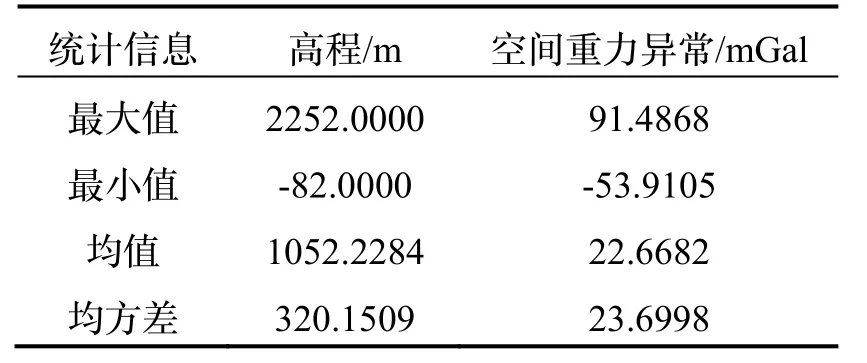
表1 高程和實測點空間重力異常統計表Tab.1 Statistics table of free-air gravity anomaly and elevation

為驗證本文所提方法的正確性，隨機選擇計算區內894 點為建模點（圓點），其余895 個點為檢核點（三角點），設計如下對比實驗：

方案一：直接格網化方法，利用傳統的格網化方法直接對實驗區內的建模點進行數據格網化，格網化時采用物理大地測量學中常用的 Kriging 插值方法[17,18]，其為區域原始數據對估計點進行的最優無偏估計。利用離散建模點位置信息和空間重力異常得到檢核點空間重力異常數據，最后和檢核點實測數據進行對比，從而得到本方案的格網化精度；

方案二：利用本文提出的“計算-移去-擬合-恢復”格網化方法，并結合實驗區高精度、高分辨率的地形數據和密度信息構造計算區域的均衡改正、地形改正和層間改正項，在建模點移去各項改正，得到建模點均衡重力異常，利用Kriging 格網化方法將實驗區格網化均衡異常格網化；最后根據點所在網格恢復移去項（均衡改正和布格改正），得到檢核點空間重力異常，并和檢核點實測數據進行對比，分析格網化精度。

2.1 方案二各類改正項分析

方案二“計算”步驟中，均衡面深度選為40 km，地殼密度為2670 kg/m3，巖漿密度為3270 kg/m3，地形改正積分半徑選取30′，利用以上數據分別計算出中心區域地形改正、均衡改正和層間改正，計算結果見圖2、表2。

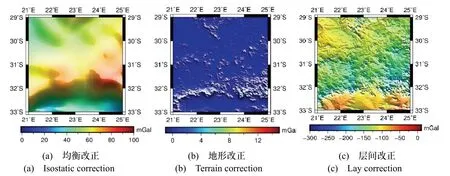
圖2 計算區各項改正示意圖Fig.2 Diagram of various corrections

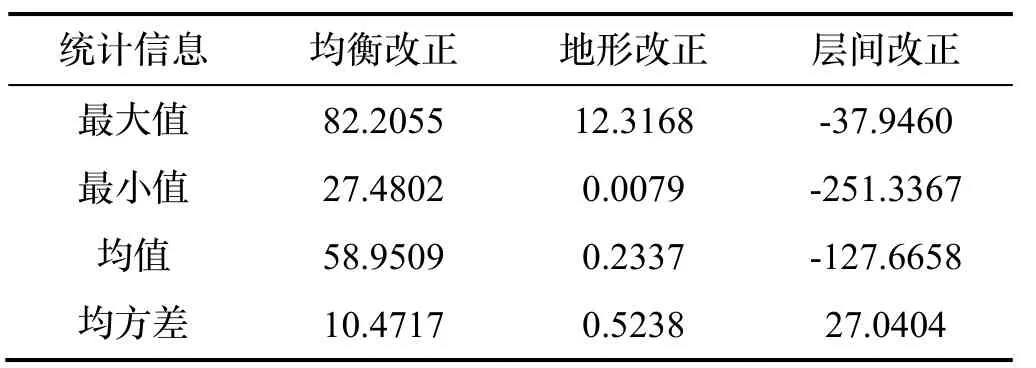
表2 各項改正統計表/mGalTab.2 Statistical table of all types of corrections/mGal

分析圖2 可以發現，在計算區內地形改正、均衡改正和層間改正的分布和地形趨勢基本一致，相似度極高，而且計算區內任何位置的改正項均可以通過嚴密公式和高分辨率的地形數據以及地殼密度項計算出來，符合“移去-恢復”理論的基本條件。

方案二“移去”過程中，依次移除建模點空間重力異常中的布格改正、均衡改正，分別得到布格重力異常和均衡重力異常，統計信息見表3，繪制如下，見趨勢圖3（為方便對比，圖中數據消除均值）。

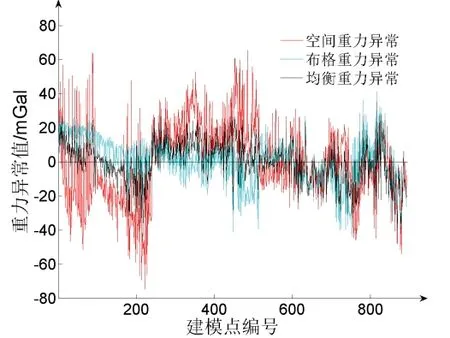
圖3 “移去”過程趨勢圖Fig.3 Diagram of “Remove” process

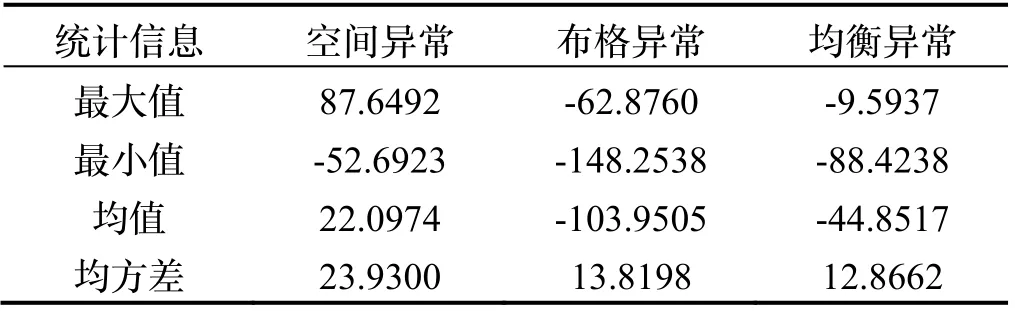
表3 建模點各項重力異常統計表/mGalTab.3 Statistics table of all types of gravity anomaly/mGal

從圖3 中可以看出，在空間重力異常中依次加入布格改正和均衡改正后，建模點的重力異常信號變化由原來的23.93 mGal 衰減為12.8662 mGal，差值閾由原來的140.3415 mGal 減小為78.8301 mGal，毛刺點明顯減少，變化趨勢更加平滑，所以空間重力異常在經過布格改正和均衡改正后更適合目標點的格網化，數據處理過程中的誤差將會減小。

2.2 不同格網化方法精度分析

按照方案一和方案二組織對比實驗，統計兩個實驗方案的結果于表4，差值見圖4。

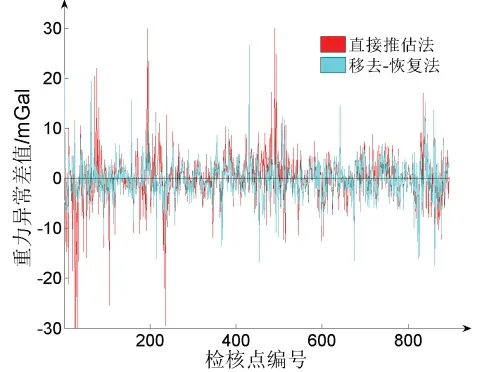
圖4 兩種方法各點差值示意圖Fig.4 Diagram of the differences between the two methods

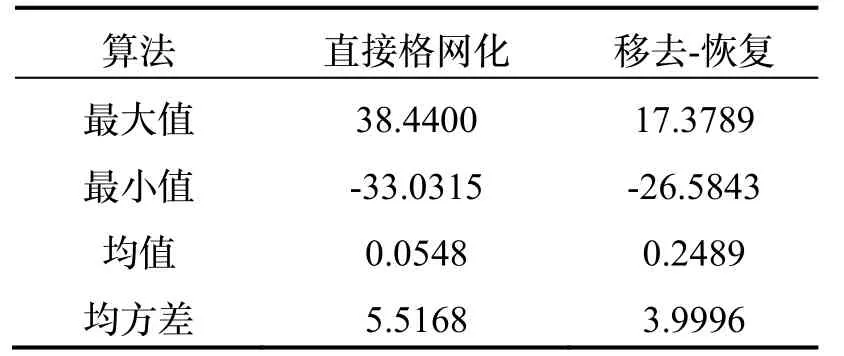
表4 兩種方法差值統計表/mGalTab.4 Statistical table of differences between two methods/mGal

實驗結果證明，無論哪種方案均能以一定的精度推估未知點的空間重力異常，其中方案一從數學角度建立已知點和未知點的聯系，進而根據建模點的空間重力異常推估出檢核點空間重力異常，檢核精度為5.5168 mGal；方案二在數學格網化的基礎上顧及了地球自身的物理信息，擬合精度為3.9996 mGal，相比于方案一，精度提升了27.5%，從精度上來看，本文提出的方法更優。“移去-恢復”法計算結果差值最大值和最小值相比傳統方法均有了一定的收斂，閾值縮小近一倍。從圖4 中看，方案二各檢核點差值分布更加集中，誤差分布更加均勻，粗差點更少。這是由于“移去-恢復”中在純數學擬合中加入了地球的物理信息，整體擬合趨勢和重力數據分布趨勢更加符合，擬合精度更好，差值分布更收斂，殘差值波動也更小。

根據以上兩種實驗方案，利用計算區內全部的1789 個重力實測數據作為建模數據，構造出計算區內1′分辨率的空間重力異常，得到實驗結果如圖5 所示，再將1789 個建模數據作為檢核數據驗證算法的自洽性，統計結果見表5 和圖6。

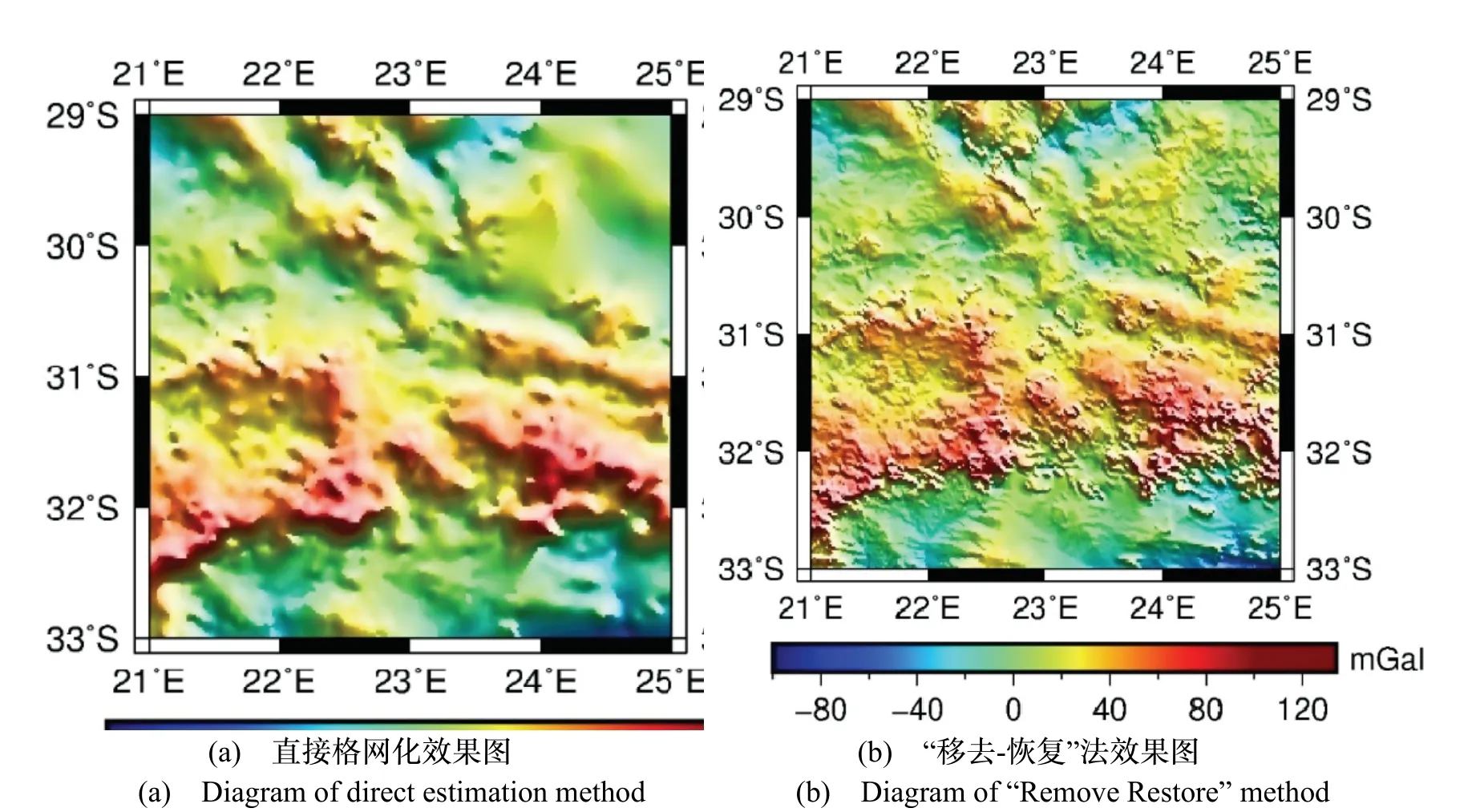
圖5 兩種方法構造的區域重力異常圖Fig.5 Regional Free-air gravity anomaly constructed by two methods

圖6 和表5 表明，本文提出的“計算-移去-推估-恢復”方法自洽性檢核的各項數學統計指標均優于直接推估方法，精度更高，系統差更小。而且在圖5 中可以看出，“移去-恢復”法所構造的局部空間重力異常包含更多的細節特征，細部信息刻畫更為詳細。這是 因為傳統的數學推估方法在計算時，會損失數據中原有的高頻信號，推估結果較為平滑；本文所提方法在“移去-恢復”的過程中，充分考慮了地形數據的影響，補齊了實驗區內空間重力異常的高頻項，使得重力場元的頻段更加完整。

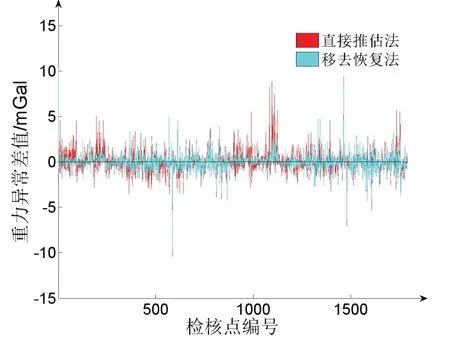
圖6 兩種方法自洽性差值示意圖Fig.6 Diagram of self-consistent error by two methods

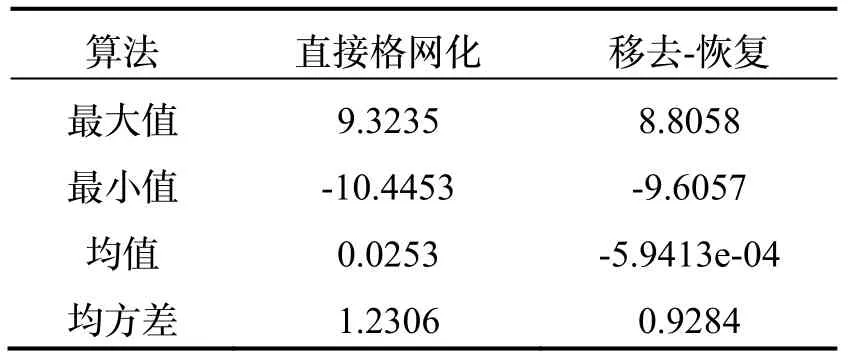
表5 兩種方法自洽性誤差值統計表/mGalTab.5 Statistics table of self-consistent error by two methods/mGal

3 結 論

本文將“移去-恢復”理論應用到局部重力數據格網化中，在格網化過程中加入地形數據和密度信息，將傳統的純數學擬合轉化為顧及地球物理場信息的格網化，通過實驗區實測數據對比實驗，得到如下結論：

（1）實測空間重力異常較為“毛糙”，直接對其進行數學擬合時，過程性誤差較大；在消除掉布格改正和均衡改正后數據變得平滑，有利于重力數據的格網化；

（2）實驗區內，“移去-恢復”方法構造的目標區域空間重力異常精度相比于Kriging 格網化的精度更高，差值波動范圍更小，而且能夠描述實驗區內重力場的細節特征，重力場元的頻段更加完整；

（3）“移去-恢復”方法利用地形數據將變化劇烈的空間重力異常轉化為較為平滑的均衡重力異常，然后再進行數據處理。可以預測，當目標區域內實測重力數據較少時，“移去-恢復”結合高分辨率地形數據方法的優勢將更加顯著。