基于ACS算法的MEMS加速度計(jì)現(xiàn)場標(biāo)定方法

喬美英，高翼飛，李宛妮，趙 巖

(河南理工大學(xué)電氣工程與自動化學(xué)院，焦作 454000)

近年來隨著微機(jī)電系統(tǒng)（Micro-Alectro-Mechanical System, MEMS）技術(shù)的快速發(fā)展，低成本、低功耗型傳感器得到了廣泛應(yīng)用。MEMS 加速度計(jì)更是在無人機(jī)、組合導(dǎo)航和醫(yī)療保健[1]等多領(lǐng)域都發(fā)揮著重要的作用。由于低成本MEMS 加速度計(jì)易受生產(chǎn)工藝及安裝的影響，導(dǎo)致實(shí)際測量值含有較大測量誤差，無法滿足精度要求。因此對MEMS 加速度計(jì)的標(biāo)定是必要的。

目前加速度計(jì)的標(biāo)定方法分為實(shí)驗(yàn)室標(biāo)定法和現(xiàn)場標(biāo)定法[2]。實(shí)驗(yàn)室標(biāo)定法是通過高精密的測量儀器標(biāo)定加速度計(jì)，標(biāo)定結(jié)果較為準(zhǔn)確，但需要較好的設(shè)施保障。現(xiàn)場標(biāo)定法的引入解決了這一困難，通過獲取現(xiàn)場數(shù)據(jù)，使用算法處理數(shù)據(jù)完成標(biāo)定。

常用的算法有橢球擬合法、高斯牛頓法、列文伯格-馬夸爾特（Levenberg-Marquardt, L-M）算法等，文獻(xiàn)[3]使用改進(jìn)的L-M 算法標(biāo)定加速度計(jì)，但模型為線性模型且十分依賴初始信息。文獻(xiàn)[4]使用高斯-牛頓法對水下多信號導(dǎo)航系統(tǒng)進(jìn)行校準(zhǔn)，將非線性問題近似成線性問題處理。近年來隨著智能優(yōu)化算法的不斷研究，越來越多智能算法也應(yīng)用到了現(xiàn)場標(biāo)定問題中。目前主流的群體智能優(yōu)化算法有：遺傳算法（Genetic Algorithm, GA）、粒子群（Particle Swarm Optimization, PSO）算法、布谷鳥搜索（Cuckoo Search, CS）算法等。文獻(xiàn)[5][6]分別使用GA 和PSO 算法對加速度計(jì)進(jìn)行現(xiàn)場標(biāo)定，但兩種算法的標(biāo)定結(jié)果并不理想，且容易陷入局部最優(yōu)情況。文獻(xiàn)[7]提出的CS 算法在處理非線性問題時，具有較強(qiáng)的全局搜索能力，但算法存在收斂速度較慢的問題。

針對上述問題，為快速、準(zhǔn)確地對加速度計(jì)進(jìn)行現(xiàn)場標(biāo)定，本文引入改進(jìn)的自適應(yīng)CS 算法標(biāo)定加速度計(jì)。其具體過程為：首先對加速度計(jì)測量誤差進(jìn)行分析，建立其誤差模型。然后構(gòu)建了標(biāo)量約束目標(biāo)函數(shù)，并通過自適應(yīng)權(quán)重和自適應(yīng)調(diào)節(jié)因子對CS 算法進(jìn)行了自適應(yīng)改進(jìn)。最后采用改進(jìn)后的自適應(yīng)布谷鳥搜索（Adaptive Cuckoo Search, ACS）算法進(jìn)行最優(yōu)化求解，得到待標(biāo)定的誤差參數(shù)。實(shí)驗(yàn)結(jié)果表明，本文提出的方法能準(zhǔn)確地標(biāo)定加速度計(jì)，是一種有效的現(xiàn)場標(biāo)定方法。

1 MEMS 加速度計(jì)誤差模型

1.1 誤差分析及模型建立

理想情況下三軸加速度計(jì)三個敏感軸是互相正交的，但由于生產(chǎn)安裝等因素使三個敏感軸處于非正交位置。為標(biāo)定這部分安裝誤差，指定加速度計(jì)上理想的正交坐標(biāo)系為t 系，敏感軸實(shí)際構(gòu)成的坐標(biāo)系為s系。將加速度矢量a 從t 系投影到s 系，得到包含安裝誤差的輸出模型如式(1)所示。由于非正交安裝誤差角均為小角，所以坐標(biāo)系之間的轉(zhuǎn)換矩陣可寫為式(2)。

其中 as、at表示加速度在s 系和t 系的投影；K*為非正交安裝誤差矩陣；θxz、θxy、θyx、θyz、θzx、θzy為s 系與t 系z 之間的誤差角，如圖1 所示。

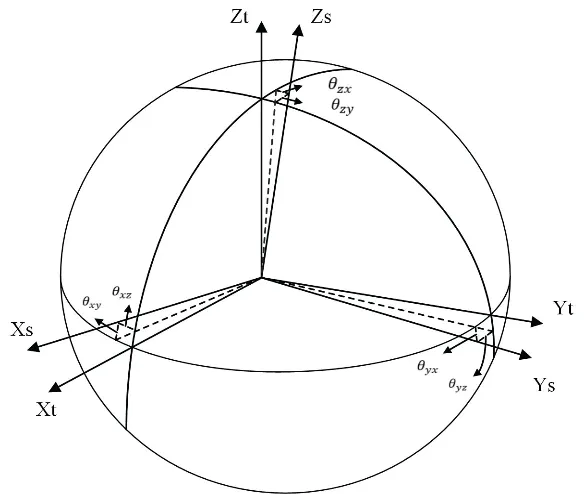
圖1 非正交安裝誤差角Fig.1 Non-orthogonal installation error angle

對非正交安裝誤差矩陣K*進(jìn)行QR 分解變換[8]如式(3)所示，將非正交安裝誤差矩陣分解為正交矩陣Q 和主對角線元素為1 的三角矩陣K。

其中正交矩陣Q 的含義是：將t 系和s 系的某一軸對準(zhǔn)。假設(shè)通過初始方位對準(zhǔn)能將s 系與t 系的x軸對準(zhǔn)，非正交安裝誤差矩陣可簡化為K ，如式(4)所示：

將比例因子誤差和偏置誤差考慮進(jìn)模型，則加速度計(jì)誤差模型變?yōu)椋?/p>

其中比例因子誤差矩陣 S =diag( kx, ky, kz)，偏置誤差向量B =[ bx, by, bz]T。由式(5)得：

1.2 標(biāo)量約束目標(biāo)函數(shù)

本文研究靜基座條件下的標(biāo)定。在靜基座條件下，無論加速度計(jì)處于任何位置，所測加速度恒等于重力加速度。參考Hamid[9]等人設(shè)置的目標(biāo)函數(shù)，本文從標(biāo)定結(jié)果的方向性原則考慮，構(gòu)造了新的標(biāo)量約束目標(biāo)函數(shù)。Hamid 使用的目標(biāo)函數(shù)如式(7)所示：

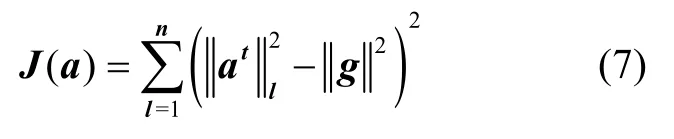
其中，n 為獲取的數(shù)據(jù)個數(shù)，重力加速度g=[ gx, gy, gz]T(g 取9.8)。使用該模型標(biāo)定加速度計(jì)會出現(xiàn)標(biāo)定后加速度矢量雖然能分布在以重力矢量模為半徑的球面上，但和重力矢量不重合。

究其原因：僅以矢量進(jìn)行約束時，其針對各分量的標(biāo)量約束較弱。因此，本文從方向性原則出發(fā)，對加速度矢量各分量的標(biāo)量進(jìn)行約束，并建立對應(yīng)的標(biāo)量約束目標(biāo)函數(shù)。避免了因標(biāo)量約束針對性弱導(dǎo)致的方向性偏差。

將式(6)展開得:

對式(8)進(jìn)行整理，寫成標(biāo)量形式。以x 軸誤差模型為例：

y 軸的目標(biāo)函數(shù) J2( ay)和z 軸的目標(biāo)函數(shù) J3( az)形式上和x 軸相同。取各軸目標(biāo)函數(shù)的平方和為總目標(biāo)函數(shù)，如式(11)所示：

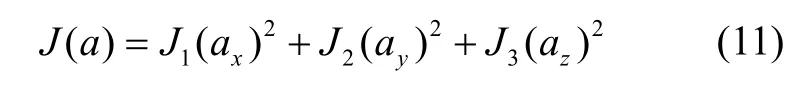
總目標(biāo)函數(shù)中待優(yōu)化的變量為9 個，將這9 個變量整理為一個解向量x x=（bxbybzkxkykzθyzθzyθzx）T。為快速、準(zhǔn)確地優(yōu)化非線性目標(biāo)函數(shù)求得解向量x 的全局最優(yōu)解，本文通過提出自適應(yīng)權(quán)重和引出自適應(yīng)因子對CS算法進(jìn)行自適應(yīng)改進(jìn)。

2 自適應(yīng)布谷鳥搜索算法

2.1 布谷鳥搜索算法

布谷鳥搜索(Cuckoo Search, CS)算法是Xin-She Yang 和Suash Deb 在2009 年提出的一種群體優(yōu)化算法[7]。該算法將布谷鳥的占巢寄生特性和萊維飛行（lévy Flights）結(jié)合起來，并通過發(fā)現(xiàn)概率調(diào)節(jié)局部隨機(jī)游走，從而取得最優(yōu)解。其中l(wèi)évy 飛行和隨機(jī)游走是控制算法全局搜索和局部搜索的關(guān)鍵：

1、lévy 飛行是算法的全局搜索策略，其實(shí)質(zhì)是在解空間內(nèi)生成滿足萊維分布的步長(長短交替的步長)來更新解向量。該策略由兩個獨(dú)立的正態(tài)分布構(gòu)成，生成服從lévy 分布的隨機(jī)步長r：

其中u～N （0,σ2）,v ～N （ 0,1）， 標(biāo)準(zhǔn)差參數(shù)β 取1.5。該策略的更新公式為：

2、隨機(jī)游走是算法的局部搜索策略，該策略的更新公式為：

其中i、j、k 表示解向量x 的不同元素(i ≠ j ≠ k)，ε 是滿足在(0,1)上均勻分布的隨機(jī)數(shù)，Pa表示發(fā)現(xiàn)被拋棄或建立新巢的概率(本文取0.25)。

2.2 自適應(yīng)改進(jìn)

CS 算法在優(yōu)化多變量函數(shù)時，由于lévy 飛行更新的大步長而具有較強(qiáng)的全局搜索能力，但在算法后期lévy 飛行更新的大步長則會影響局部搜索能力，降低算法收斂速度[10,11]。針對此問題，本文從兩個方面對CS 算法進(jìn)行了自適應(yīng)改進(jìn)：(1)通過自適應(yīng)權(quán)重將lévy 飛行和隨機(jī)游走融合，提高算法局部搜索能力。(2)引入自適應(yīng)因子調(diào)節(jié)Pa，在擴(kuò)大局部搜索能力的同時兼顧算法全局性。通過這兩部分的自適應(yīng)改進(jìn)，提高算法的收斂速度。

2.2.1 自適應(yīng)權(quán)重

通過設(shè)置自適應(yīng)權(quán)重將兩種飛行策略融合，提高算法中后期的局部搜索能力。

以lévy 飛行的自適應(yīng)權(quán)重為主進(jìn)行分析：lévy 飛行生成的步長分布是典型的重尾分布,具有較高的概率出現(xiàn)大步長。考慮到權(quán)重的大小影響著算法的全局和局部搜索，自適應(yīng)權(quán)重應(yīng)在算法中后期抑制大步長的產(chǎn)生，提高局部搜索能力。

若采用線性函數(shù)形式調(diào)節(jié)重尾分布現(xiàn)象，難以平衡算法局部搜索和全局搜索。因此使用非線性形式設(shè)置兩種策略的權(quán)重，在算法前期緩慢地降低lévy 飛行的權(quán)重，保證良好的全局搜索能力，中后期快速地降低其權(quán)重值，同時增大隨機(jī)游走的權(quán)重，提高局部搜索能力，加快收斂速度，動態(tài)地平衡算法的全局性和局部性。lévy 飛行策略的自適應(yīng)權(quán)重 ω1為：

2.2.2 自適應(yīng)因子δ

發(fā)現(xiàn)或建立新巢的概率Pa直接控制著算法局部搜索，但考慮到種群適應(yīng)性，發(fā)現(xiàn)概率Pa應(yīng)隨著種群的進(jìn)化不斷減小。因此引入自適應(yīng)因子δ使發(fā)現(xiàn)概率Pa受算法迭代次數(shù)控制。將自適應(yīng)因子調(diào)整后的發(fā)現(xiàn)概率 Pa′定義為：

為保持算法的多樣性，在算法前期發(fā)現(xiàn)概率 Pa′和原算法Pa相當(dāng)，隨著種群的進(jìn)化，發(fā)現(xiàn)概率 Pa′先快速下降再緩慢下降至穩(wěn)定。自適應(yīng)因子δ為：

將自適應(yīng)改進(jìn)后的CS 算法稱為自適應(yīng)布谷鳥搜索（adaptive cuckoo search, ACS）算法，使用ACS 算法對加速度計(jì)進(jìn)行現(xiàn)場標(biāo)定的整體流程如圖2 所示。

圖2 基于ACS 算法的加速度計(jì)現(xiàn)場標(biāo)定Fig. 2 Field calibration of accelerometer based on ACS algorithm

下節(jié)通過仿真實(shí)驗(yàn)和實(shí)測實(shí)驗(yàn)，驗(yàn)證ACS 算法的有效性及所提方法的可行性。

3 實(shí)驗(yàn)與分析

3.1 仿真實(shí)驗(yàn)

隨機(jī)選取分布在單位球體上的1000 個點(diǎn)，將這些點(diǎn)視為處于不同位置下的重力矢量，即當(dāng)?shù)刂亓χ怠Ｕ`差參數(shù)的設(shè)定如表1 所示。

表1 加速度計(jì)誤差參數(shù)設(shè)置Tab.1 Accelerometer error parameter setting

將加入誤差后的點(diǎn)作為加速度計(jì)的測量值點(diǎn)。當(dāng)?shù)刂亓χ岛蜏y量值在空間上的分布如圖 3 所示(g=9.8m/s2)。其中三角點(diǎn)“Δ”表示測量值點(diǎn)，星花點(diǎn)“*”表示當(dāng)?shù)刂亓χ迭c(diǎn)。

圖3 重力值點(diǎn)與測量值點(diǎn)Fig.3 Gravity value points and measured value points

算法的初始參數(shù)設(shè)置如表2 所示。

表2 ACS 算法初始參數(shù)Tab.2 Initial parameters of ACS algorithm

將目標(biāo)函數(shù)式(11)設(shè)置為適應(yīng)度函數(shù)，經(jīng)ACS 算法標(biāo)定結(jié)果如表3 和表4 所示。

表3 誤差矩陣1Tab.3 Error matrix 1

從表3 和表4 中可以看出ACS 算法標(biāo)定的誤差參數(shù)和設(shè)定參數(shù)基本一致，準(zhǔn)確地標(biāo)定出了加速度計(jì)的誤差參數(shù)。標(biāo)定后的加速度如圖4 中方塊點(diǎn)“□”所示。可以看出標(biāo)定后數(shù)據(jù)點(diǎn)和當(dāng)?shù)刂亓χ迭c(diǎn)基本重合。

表4 零偏誤差1Tab.4 Zero offset error 1

圖4 校準(zhǔn)前后點(diǎn)的分布Fig.4 Distribution of points before and after calibration

為驗(yàn)證ACS 算法標(biāo)定加速度計(jì)的準(zhǔn)確性，將ACS算法、CS 算法和PSO 算法的標(biāo)定結(jié)果進(jìn)行對比。三種算法采用相同的初始參數(shù)設(shè)置(表2)，且采用相同的適應(yīng)度函數(shù)。表5 和表6 給出了三種算法標(biāo)定的誤差參數(shù)。

表5 誤差矩陣2Tab.5 Error matrix 2

從表5 和表6 中可以看出CS 算法和ACS 算法都準(zhǔn)確地標(biāo)定出了加速度計(jì)的誤差參數(shù)，PSO 算法由于陷入局部最優(yōu)情況，導(dǎo)致標(biāo)定結(jié)果與設(shè)定值相差較大。

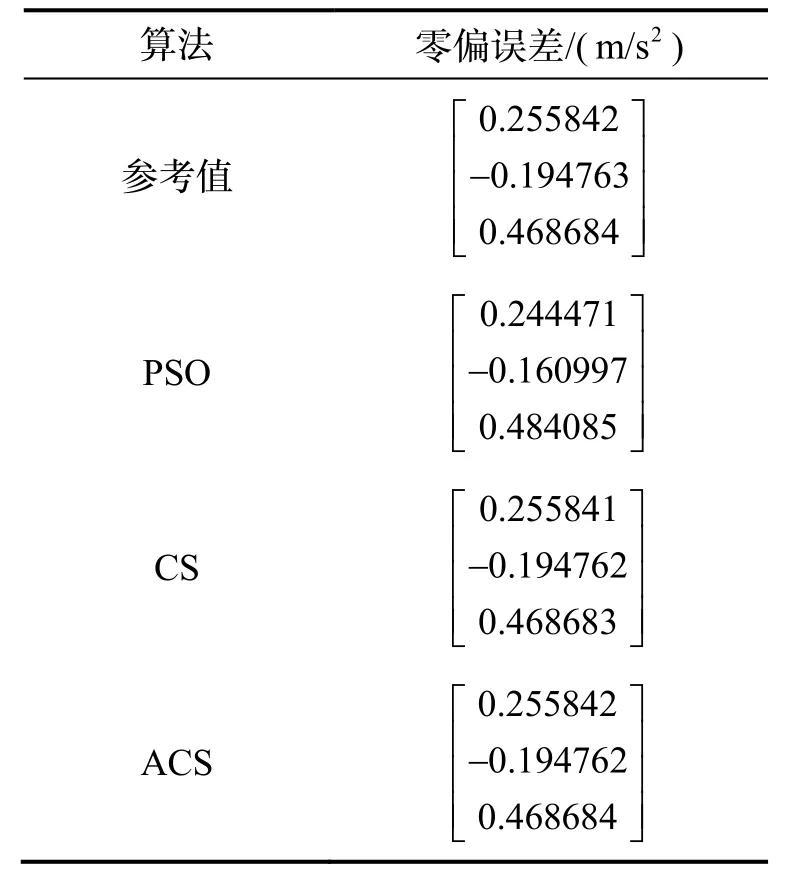
表6 零偏誤差2Tab.6 Zero offset error 2

3.2 算法效率對比

為驗(yàn)證對CS 算法自適應(yīng)改進(jìn)的有效性，將CS算法和ACS 的初始參數(shù)設(shè)置一致，比較兩種算法的收斂速度和迭代次數(shù)。表7 展示了CS 算法和ACS 算法在不同數(shù)量數(shù)據(jù)點(diǎn)下的平均迭代次數(shù)。圖5(a)和圖5(b)分別為1000 個數(shù)據(jù)點(diǎn)下ACS 算法與CS 算法迭代次數(shù)和適應(yīng)度值的關(guān)系圖。

表7 改進(jìn)前后算法平均迭代次數(shù)Tab.7 The average iteration times of the algorithm before and after improvement

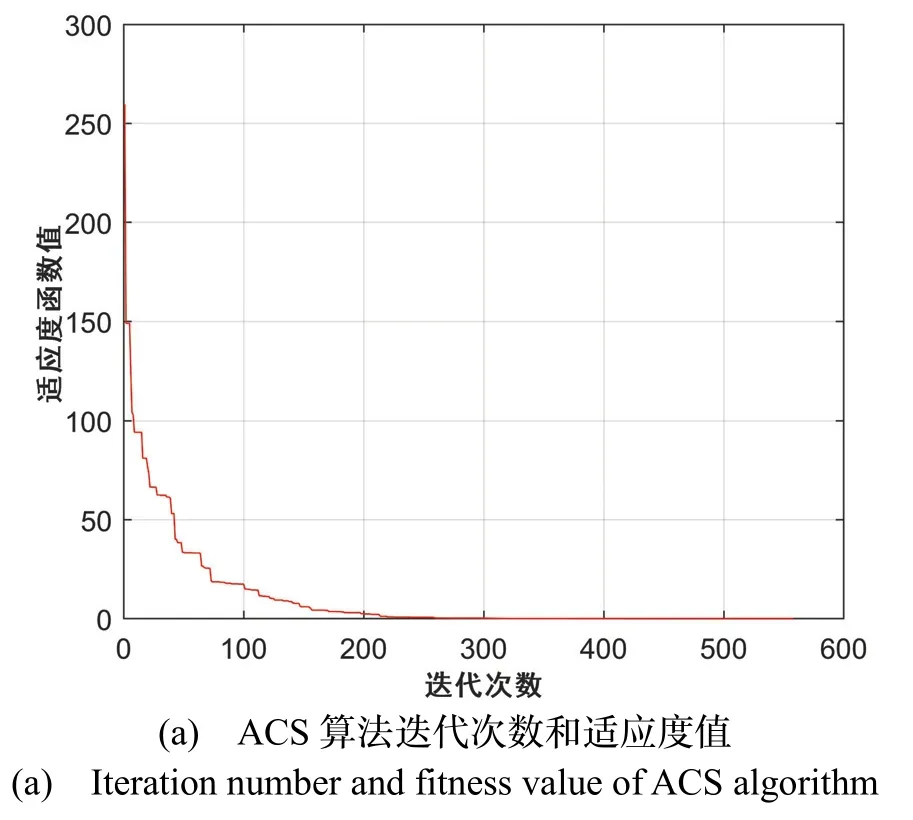
表7 中可以看出ACS 算法的迭代次數(shù)有明顯的下降。當(dāng)數(shù)據(jù)點(diǎn)數(shù)為100 時，ACS 算法的平均迭代次數(shù)比CS 算法減少了約140 代左右，降低了22%；當(dāng)數(shù)據(jù)點(diǎn)數(shù)為1000 時，ACS 算法的平均迭代次數(shù)下降了約120 代左右，降低了16%。圖5(a)和圖5(b)的對比可以看出，在相同迭代次數(shù)時，ACS 算法的適應(yīng)度函數(shù)值下降得更快。

圖5 兩種算法的迭代次數(shù)和適應(yīng)度值Fig.5 Iteration number and fitness values of the two algorithms

3.3 實(shí)測實(shí)驗(yàn)

為進(jìn)一步評估ACS 算法現(xiàn)場標(biāo)定方法的有效性，對三軸MEMS 加速度計(jì)MPU6050 進(jìn)行實(shí)驗(yàn)驗(yàn)證。

首先將包含加速度計(jì)的載體安裝在如圖6 所示的無磁雙軸轉(zhuǎn)臺上，在靜基座條件下獲取不同位置的重力加速度值。

圖6 雙軸轉(zhuǎn)臺和載體傳感器Fig. 6 Dual-axis turntable and carrier sensor

通過操作轉(zhuǎn)臺，使載體俯仰角按0 °，30 °，60 °，90 °，120 °，150 °，180 °旋轉(zhuǎn)，對應(yīng)的航向角旋轉(zhuǎn)次數(shù)和角間隔為1，0 °；8，45 °；14，25.7143 °；16，22.5 °；14，25.7143 °；8，45 °；1，0 °。將這62 個位置下的加速度計(jì)輸出值進(jìn)行存儲，使用ACS 算法標(biāo)定加速度計(jì)。將算法標(biāo)定的誤差參數(shù)與實(shí)驗(yàn)室標(biāo)定法的誤差參數(shù)進(jìn)行對比。實(shí)驗(yàn)室標(biāo)定法[12]的參數(shù)如表8所示，ACS 算法標(biāo)定的參數(shù)如表9 所示。

表8 實(shí)驗(yàn)室標(biāo)定結(jié)果Tab.8 Laboratory calibration results

表9 ACS 算法標(biāo)定結(jié)果Tab.9 ACS algorithm calibration results

為了衡量兩種方法，用式(21)計(jì)算標(biāo)定后的加速度誤差，并計(jì)算均方根誤差(Root-Means-Square Error, RMSE)和標(biāo)準(zhǔn)差(Standard Deviation, SD)。圖7 為總誤差的對比結(jié)果。

其中 ail為真實(shí)加速度值，為校準(zhǔn)后加速度值，l 為測量樣本個數(shù)，

從圖7 可以看出ACS 算法現(xiàn)場標(biāo)定法的標(biāo)定誤差在峰值處明顯低于實(shí)驗(yàn)室標(biāo)定法的標(biāo)定誤差。表10給出了兩種方法的均方根誤差和標(biāo)準(zhǔn)差。所提方法相比實(shí)驗(yàn)室標(biāo)定法，均方根誤差從0.1103 降低到0.0826，降低了25.11%；標(biāo)準(zhǔn)差從0.0643 降低到0.0487，降低了24.26%。

圖7 校準(zhǔn)后總誤差對比Fig.7 Overall error comparison after calibration

表10 均方根誤差和標(biāo)準(zhǔn)差Tab.10 Root mean square error and standard deviation

考慮到現(xiàn)場標(biāo)定與轉(zhuǎn)臺試驗(yàn)測量點(diǎn)的差異性問題，為了驗(yàn)證算法的實(shí)用性，采用六面取點(diǎn)進(jìn)行驗(yàn)證，并與傳統(tǒng)六面現(xiàn)場標(biāo)定法進(jìn)行對比。六面現(xiàn)場標(biāo)定法和ACS 算法現(xiàn)場標(biāo)定法的結(jié)果如表11 和表12 所示，校準(zhǔn)后加速度誤差如圖8 所示。

表11 六面標(biāo)定法結(jié)果Tab.11 Results of six-side calibration method

表12 ACS 算法六面標(biāo)定結(jié)果Tab.12 Six-side calibration results of ACS algorithm

從圖8 和表11、12 可以看出相比于傳統(tǒng)六面法，ACS 標(biāo)定法的標(biāo)定精度穩(wěn)定，校準(zhǔn)誤差低，且對數(shù)據(jù)量并不敏感。驗(yàn)證了該方法的實(shí)用性。

圖8 校準(zhǔn)后誤差對比Fig.8 Error comparison after calibration

4 結(jié) 論

本文為快速、準(zhǔn)確地標(biāo)定加速度計(jì)，提出了一種基于ACS 算法的微加速度計(jì)現(xiàn)場標(biāo)定方法。從標(biāo)量約束的角度構(gòu)造了目標(biāo)函數(shù)，并對布谷鳥搜索算法進(jìn)行了自適應(yīng)改進(jìn)。實(shí)驗(yàn)結(jié)果表明，相比傳統(tǒng)六面標(biāo)定法以及實(shí)驗(yàn)室標(biāo)定法，收斂速度更快且標(biāo)定結(jié)果更加精確穩(wěn)定。后續(xù)將繼續(xù)對MEMS 加速度計(jì)的隨機(jī)誤差以及陀螺儀等慣性測量儀器的標(biāo)定進(jìn)行深入研究，為慣性導(dǎo)航器件的廣泛應(yīng)用夯實(shí)基礎(chǔ)。