含對數的積分之求解方法研究

李慶娟

(大連財經學院 管理學院，遼寧 大連 116622)

在一元微積分中,含對數的積分是一類常見的積分求解問題,有些題目甚至較難,求解方法往往具有較強的靈活性和技巧性,一般地,我們要根據題目中被積函數的特點采用不同的求解方法和技巧,典型的計算方法可總結為換元法、分部積分法、累次積分法、特定結論法。

1 換元法

1.1 湊微分換元法

湊微分法是計算積分的主要方法之一,又稱第一類換元法,主要是根據被積函數的特點進行相應的湊微分,進而換元求解,如果熟練的話,可省略中間的換元過程直接求出積分。

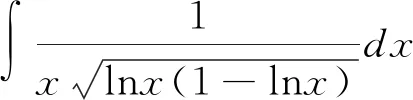
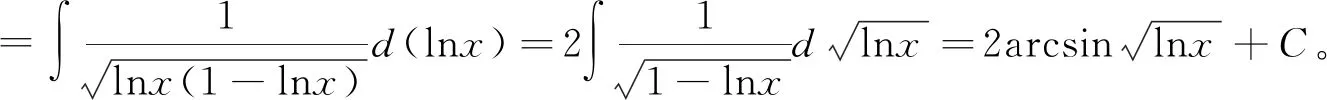
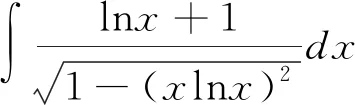
解 先觀察被積函數特點,注意到分子lnx+1=(xlnx)′,將整個分子湊微分再求解,

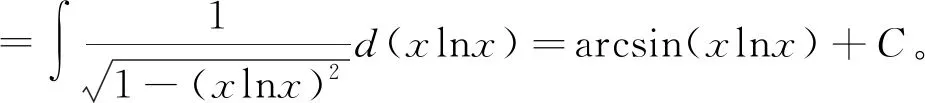
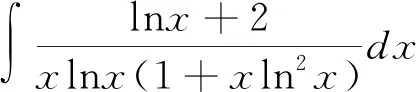
解 此題不具備直接可湊微分的項,但可以利用添項法,將分子分母同乘以lnx,這時會有(xln2x)′=ln2x+2lnx,故將分子湊微分即可

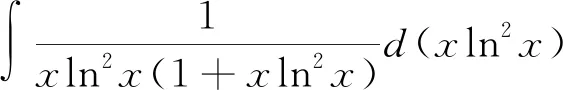
=ln|xln2x|-ln|1+xln2x|+C。

1.2 第二類換元法

第二類換元法與湊微分換元法思路不同,前者是直接采用變元進行換元,后者是先湊分再進行換元,第二類換元法中常用的換元方法主要有直接代換法、根式代換法、倒代換法、三角代換法等,它是求解積分非常重要的方法。

1.2.1 直接換元法

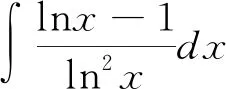
解 令t=lnx,則x=et,dx=etdt

即將不定積分分成兩個積分,選擇第一項用分部積分法求解

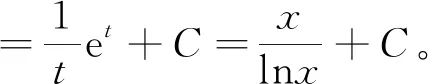
1.2.2 根式代換法

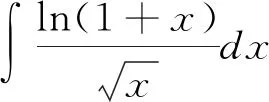
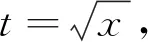
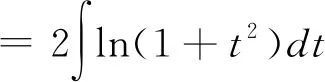
=2tln(1+t2)-4t+4arctant+C

1.2.3 三角代換法

解 令x=tant,則dx=sec2tdt,

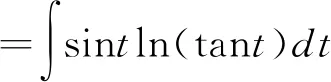
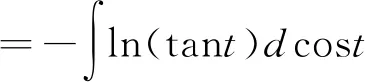
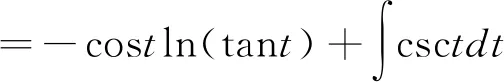
=-costln(tant)+ln|csct-cott|+C

1.2.4 倒代換法

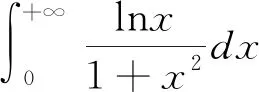
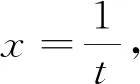
1.2.5 靈活代換法

對于含有對數和三角函數的定積分求解時,可根據被積函數和積分區間所給形式靈活采用相應的代換形式。

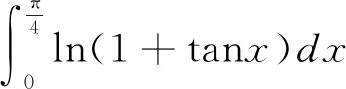
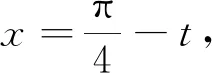
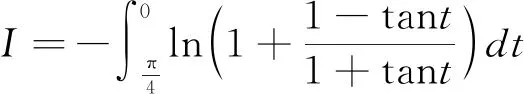
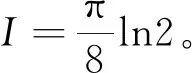
2 分部積分法

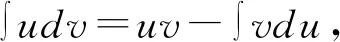
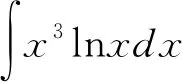
解 根據選擇標準選冪函數湊進去作為v

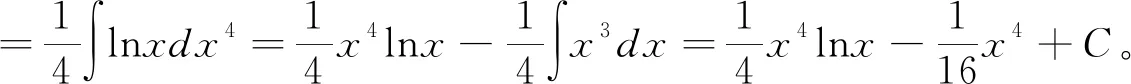
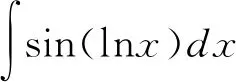
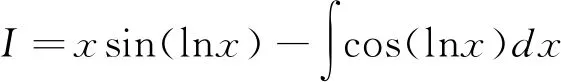
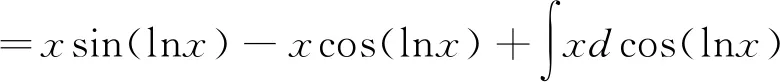
=xsin(lnx)-xcos(lnx)-I

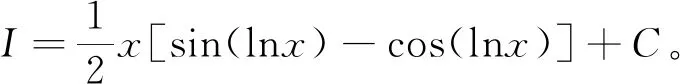
3 累次積分法

所謂累次積分法就是根據所求的定積分的形式先將其先轉化為一個二重積分,再通過改變積分次序求解對應的累次積分。

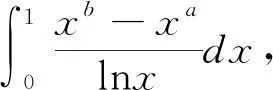
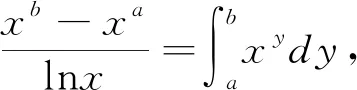
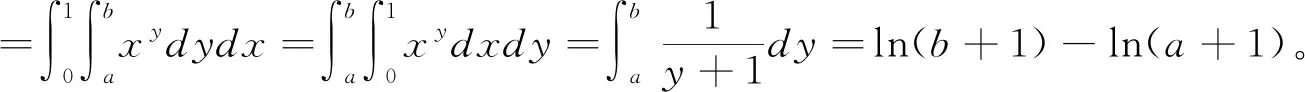
4 特定結論法

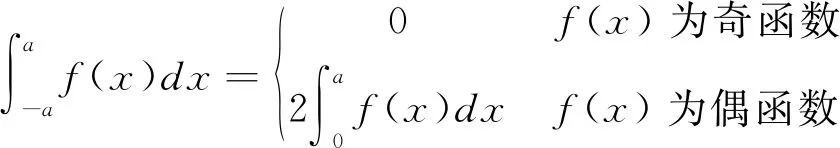
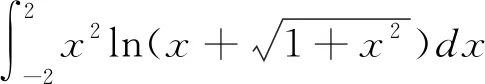
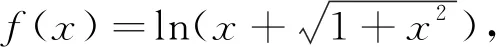
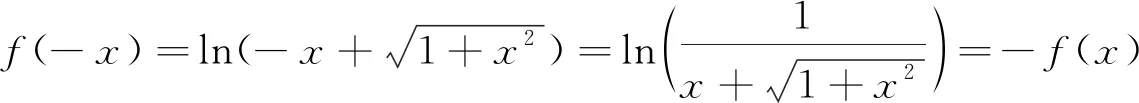
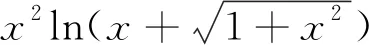
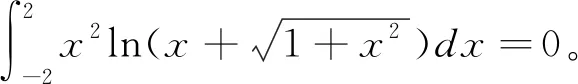
5 結束語

綜上,我們通過實例分析給出了含對數積分的幾種重要求解方法,一般地,被積函數形式不同采用的方法就有所不同,在學習積分的過程中,我們要善于思考、研究、總結和歸納,這樣再遇到此類積分時,思路將更開闊,問題會輕松解決。